Файл: Протокол от 2017г Протокол от 201 г Председатель цикловой комиссии Председатель цикловой комиссии.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 63
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
13) (1 балл) В правильной четырехугольной пирамиде
14) (1 балл) Решите уравнение sin 2x = 1.
15) (1 балл) Найдите область определения функции
Дополнительная часть
При выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Из 12 полицейских необходимо составить наряд из 5 человек. Сколькими способами это можно сделать?
17) (3 балла) Найдите корни уравнения
18) (3 балла) Апофема правильной четырехугольной пирамиды равна 15см, высота пирамиды равна 12см. Найти объём и площадь полной поверхности пирамиды.
19) (3 балла) Решите неравенство
20) (3 балла) Найдите наименьшее значение функции y = x2 – 12x + 12 на отрезке [-1 ; 3 ]
Преподаватель Петрова Л.Л.
Комитет общего и профессионального образования Ленинградской области
ГБПОУ ЛО «Волховский колледж транспортного строительства»
9 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход решения и полученный ответ.
-
(1 балл) Флакон шампуня стоит 80 рублей. Какое наибольшее количество флаконов можно купить на 500 рублей во время распродажи, когда скидка составляет 25%? -
(1 балл) Вычислите значение выражения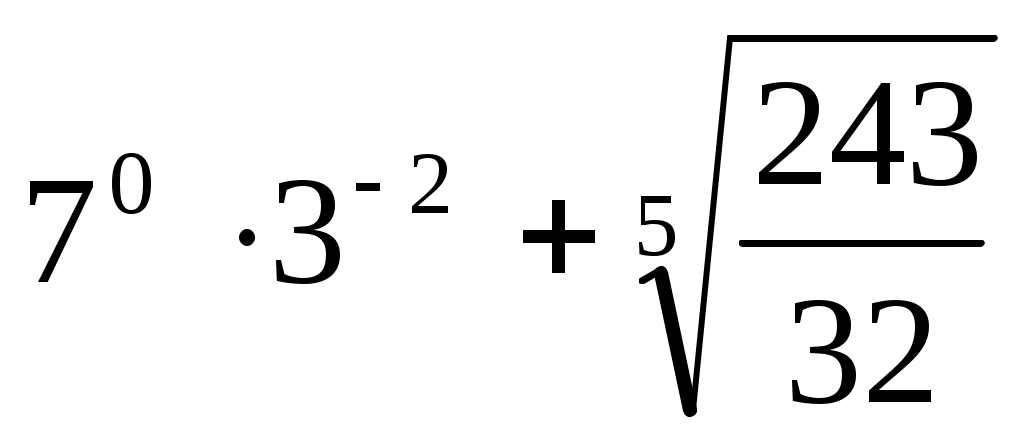 .
. -
(1 балл) Решите уравнение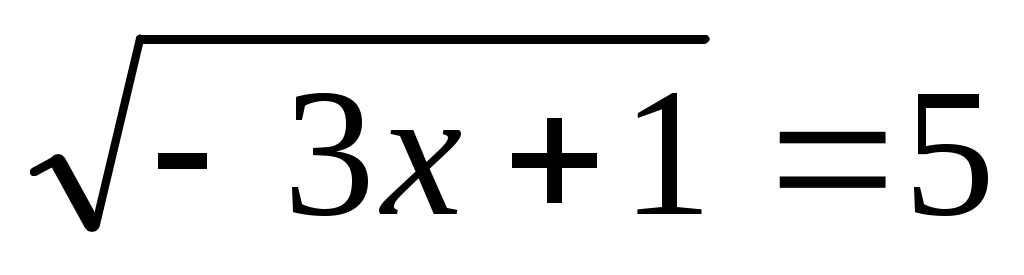 .
. -
(1 балл) Решите систему уравнений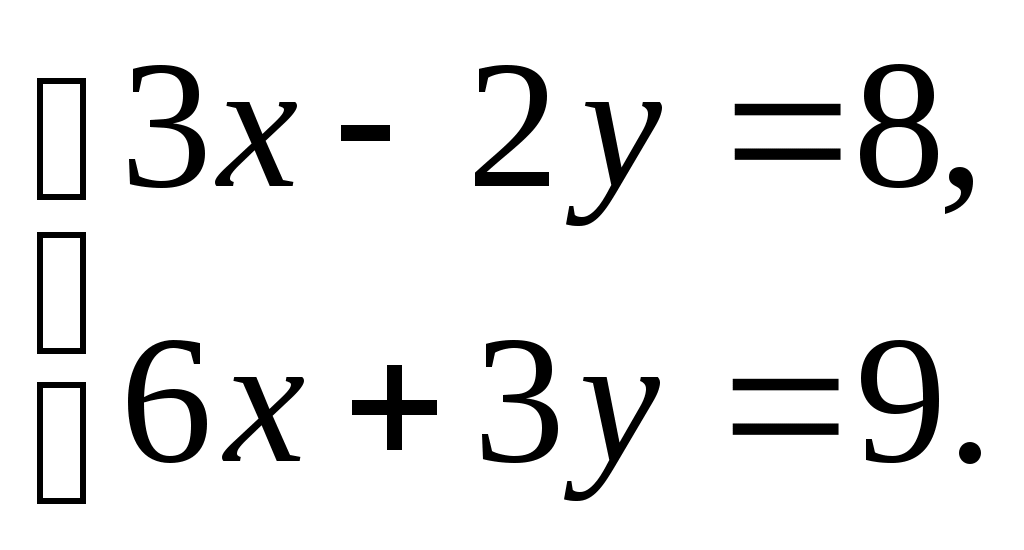
-
(1 балл) На основании основного логарифмического тождества найдите значение выражения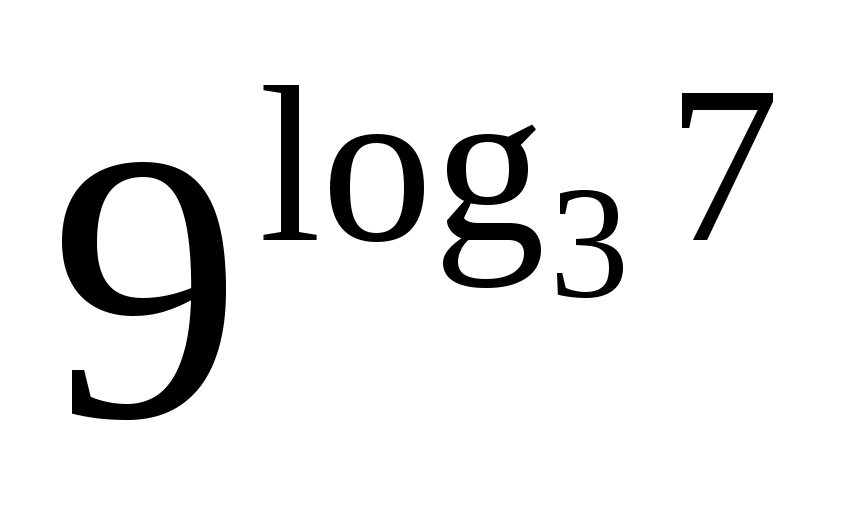 .
.
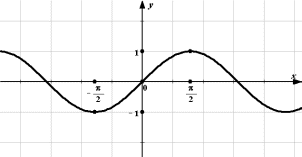
При выполнении заданий 6-9, используя график функции
-
(1 балл) Область определения функции. -
(1 балл) Наименьший положительный период функции. -
(1 балл) Множество значений функции. -
(1 балл) Наименьшее и наибольшее значения функции.
При выполнении заданий 10-15 укажите ход решения и запишите полученный ответ.
-
(1 балл) Найдите значение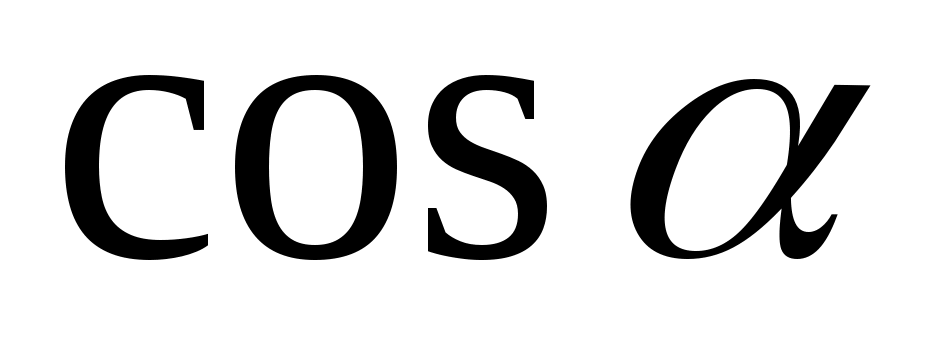 , если известно, что
, если известно, что 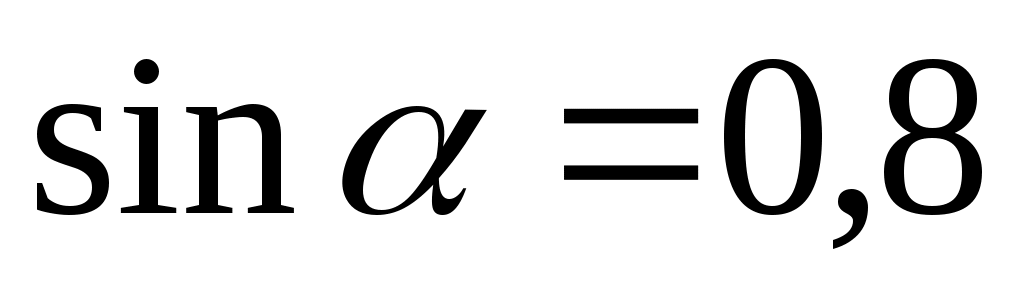 и
и 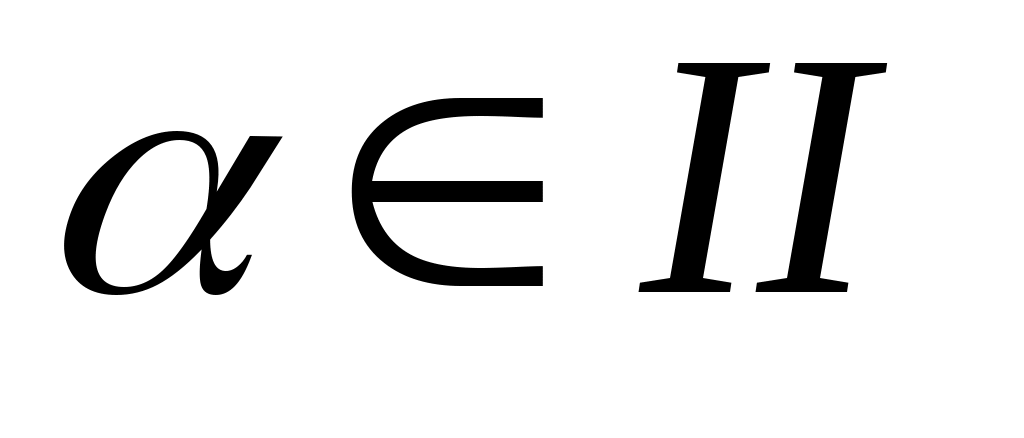 четверти.
четверти. -
(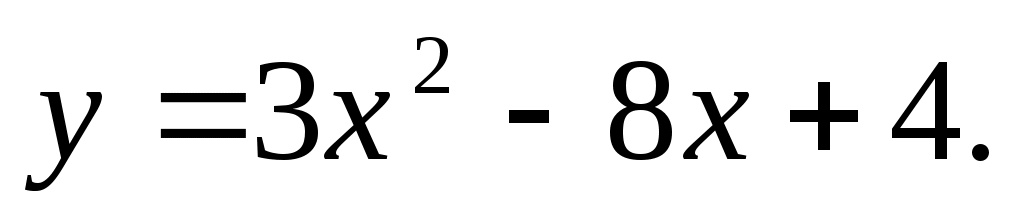 1 балл) Найдите нули функции
1 балл) Найдите нули функции -
(1 балл) Найти производную функции
-
(1 балл) В прямоугольном параллелепипеде известно, что
известно, что  ,
,  ,
, 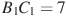 . Найдите длину ребра .
. Найдите длину ребра . -
(1 балл) Решите уравнение cos x = –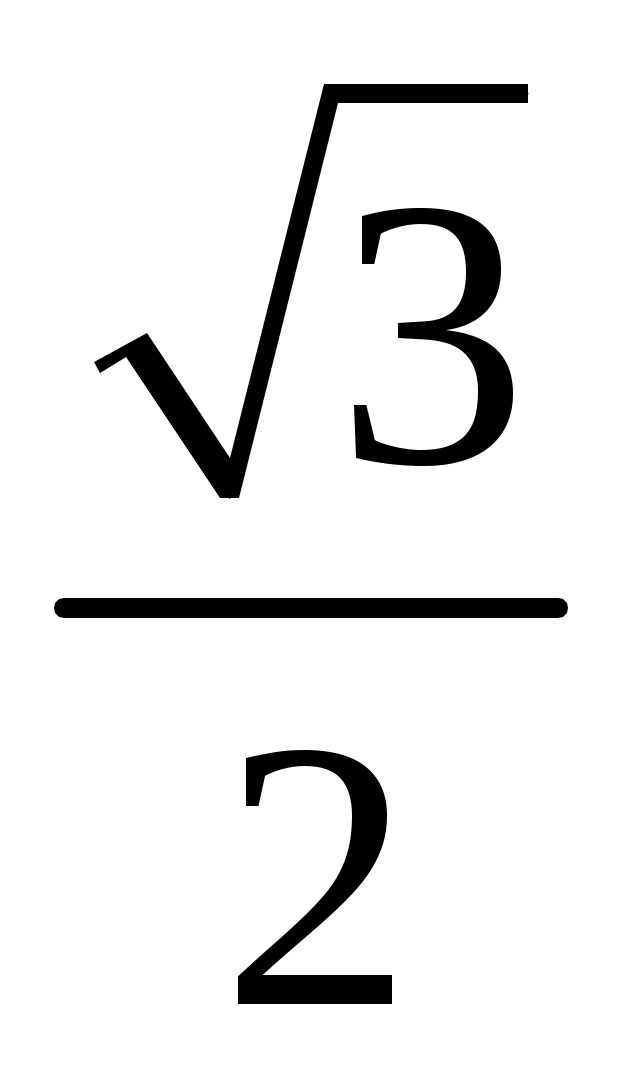 .
. -
(1 балл) Найдите область определения функции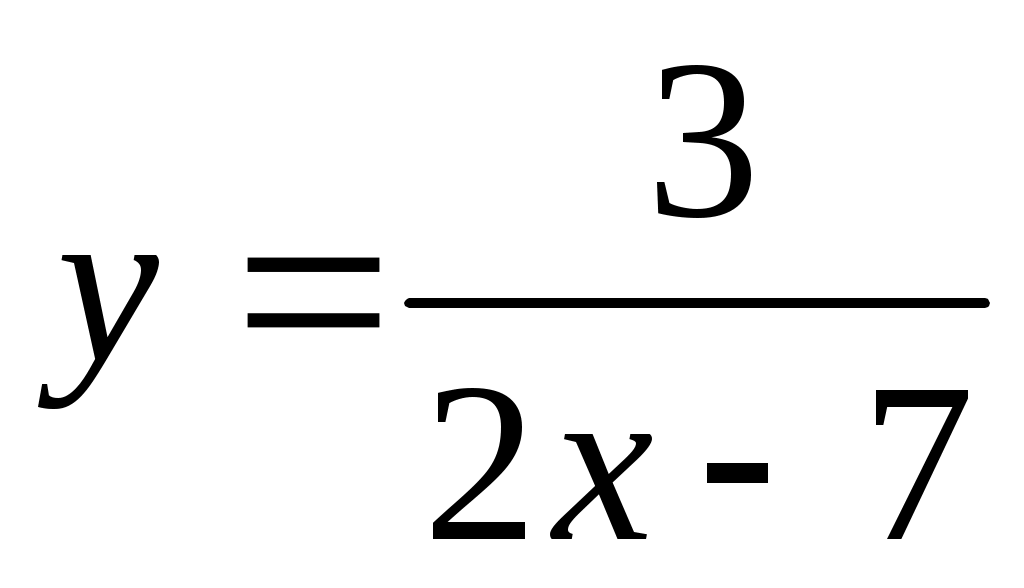
Дополнительная часть
При выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Сколько 3-значных чисел можно составить из множества цифр 1,2,3,4,5,6,7,8,9 а) без повторений; б) с повторениями?
17) (3 балла) Найдите корни уравнения
18) (3 балла) Сторона основания правильной четырехугольной пирамиды равна 12см, высота пирамиды равна 8см. Найти площадь полной поверхности пирамиды.
19) (3 балла) Решите неравенство
20) (3 балла) Найти интервалы возрастания и убывания функции y = x4 – 32x2 – 75
Преподаватель Петрова Л.Л.
Комитет общего и профессионального образования Ленинградской области
ГБПОУ ЛО «Волховский колледж транспортного строительства»
8 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход решения и полученный ответ.
-
(1 балл) Билет на автобус стоит 15 рублей. Какое наибольшее число билетов можно будет купить на 100 рублей после повышения цены билета на 20%? -
(1 балл) Вычислите значение выражения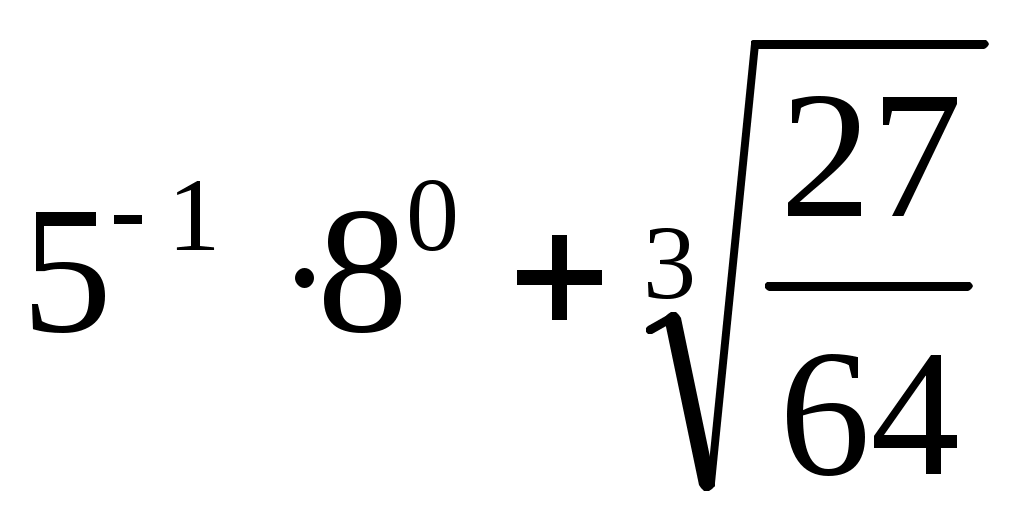 .
. -
(1 балл) Решите уравнение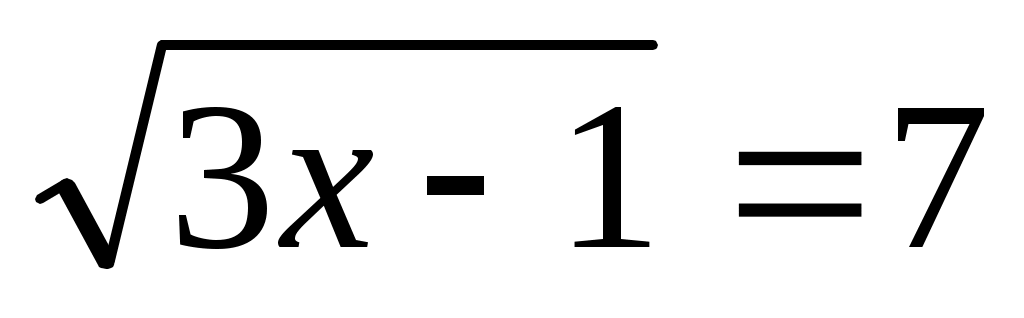
-
(1 балл) Решите систему уравнений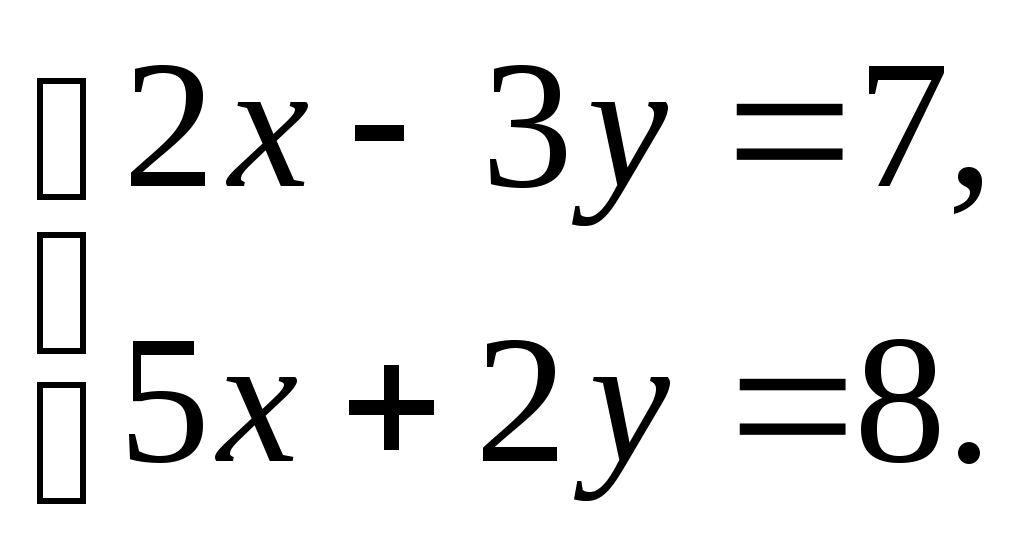
-
(1 балл) Найдите значение выражения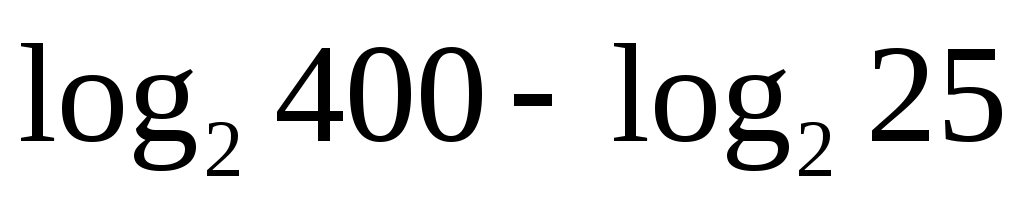 .
.
П
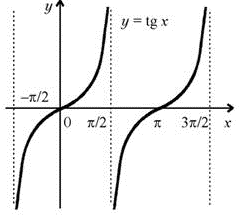 ри выполнении заданий 6-9, используя график функции
ри выполнении заданий 6-9, используя график функции -
(1 балл) Область определения функции. -
(1 балл) Множество значений функции. -
(1 балл) Нули функции. -
(1 балл) Четность, нечетность функции.
При выполнении заданий 10-15 укажите ход решения и запишите полученный ответ.
-
(1 балл) Найдите значение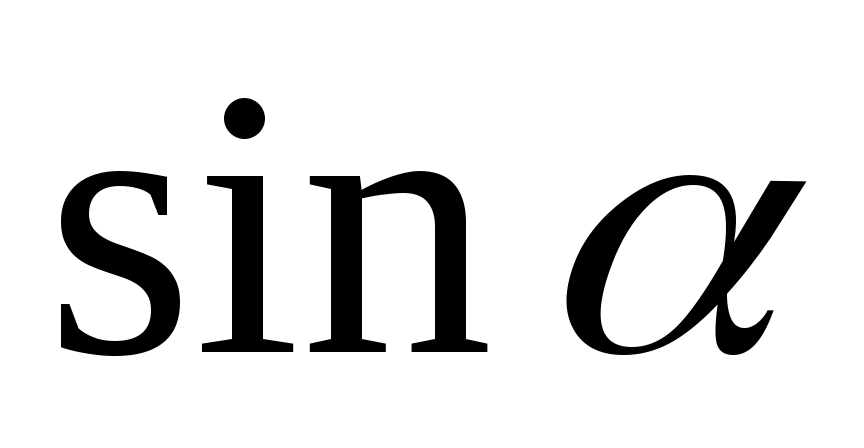 , если известно, что
, если известно, что 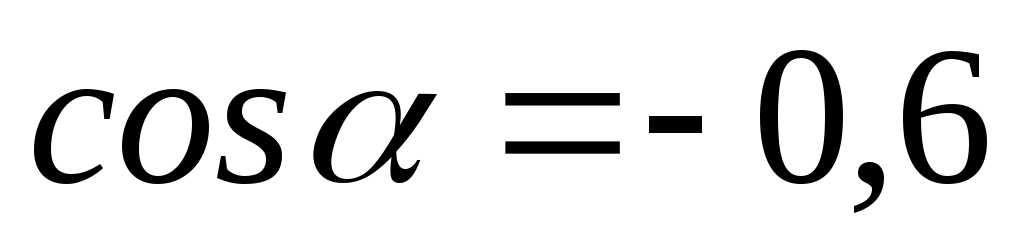 и
и 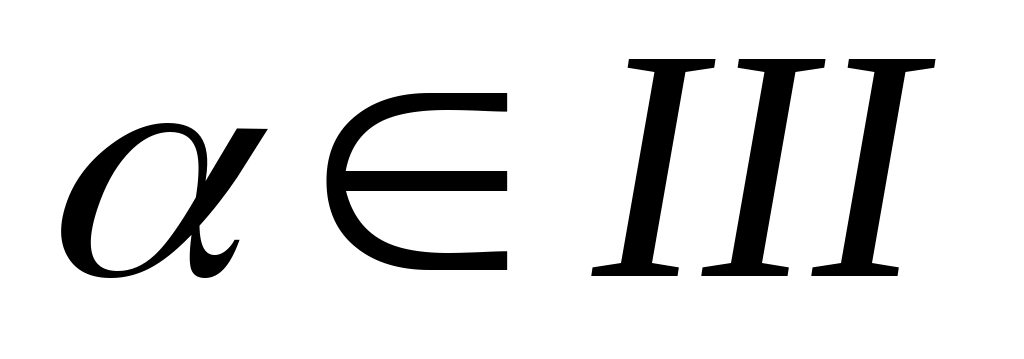 четверти.
четверти. -
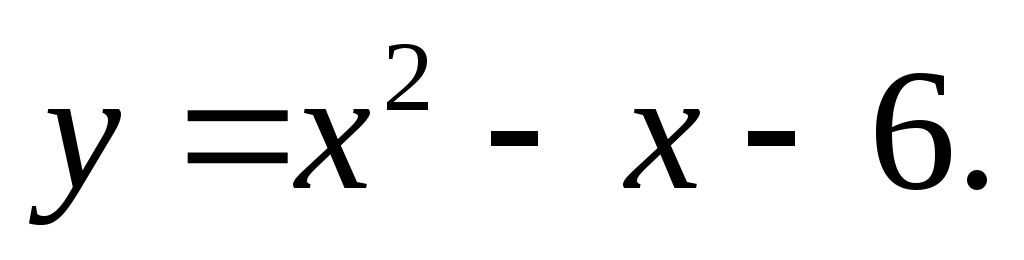 (1 балл) Найдите нули функции
(1 балл) Найдите нули функции -
(1 балл) Найти производную функции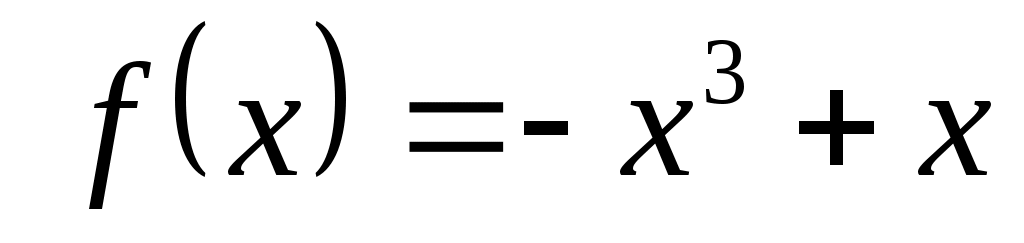
13) (1 балл) В правильной четырехугольной пирамиде
14) (1 балл) Решите уравнение cos3 x = –1.
15) (1 балл) Найдите область определения функции
Дополнительная часть
При выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 7.
17) (3 балла) Найдите корни уравнения
18) (3 балла) Апофема правильной четырехугольной пирамиды равна 10см, высота пирамиды равна 8см. Найти объём и площадь полной поверхности пирамиды.
19) (3 балла) Решите неравенство
20) (3 балла) Найдите экстремумы функции y(x) = 2x3 – 3x2 – 12x + 5
выяснить их род.
Преподаватель Петрова Л.Л.
Комитет общего и профессионального образования Ленинградской области
ГБПОУ ЛО «Волховский колледж транспортного строительства»
7 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход решения и полученный ответ.
-
(1 балл) Из 75 девятиклассников школы 15 человека приняли участие в городских спортивных соревнованиях. Сколько процентов девятиклассников не принимали участия в этих соревнованиях? -
(1 балл) Вычислите значение выражения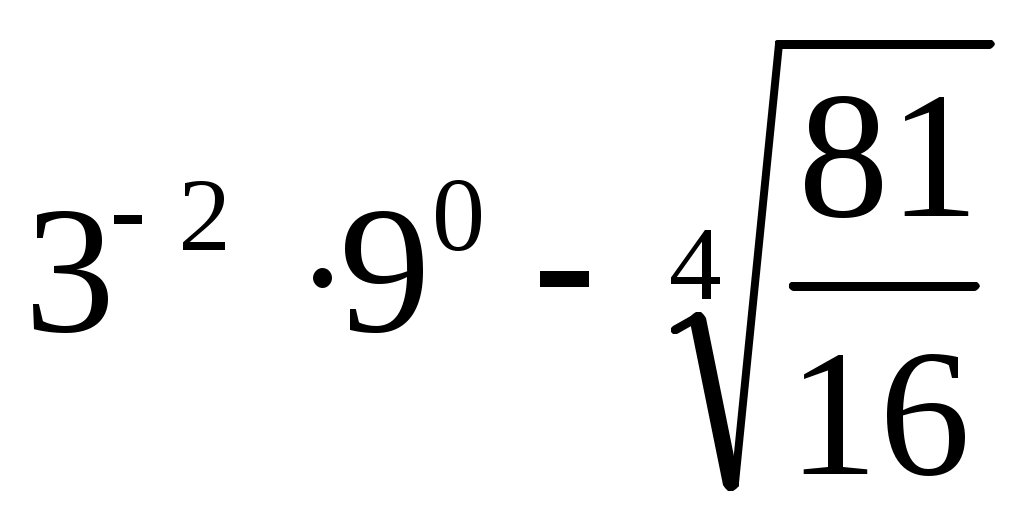 .
. -
(1 балл) Решите уравнение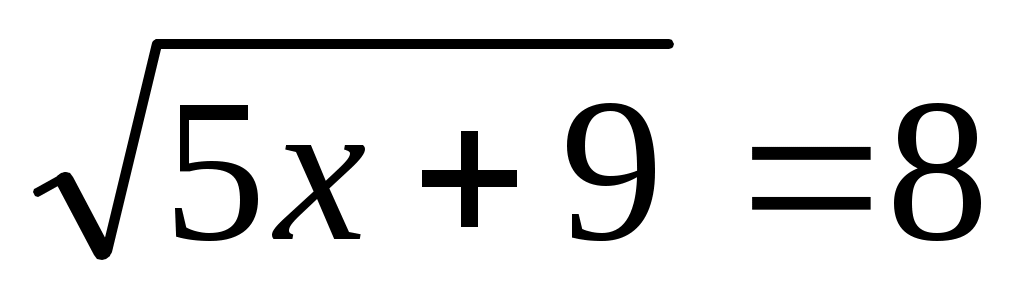 .
. -
(1 балл) Решите систему уравнений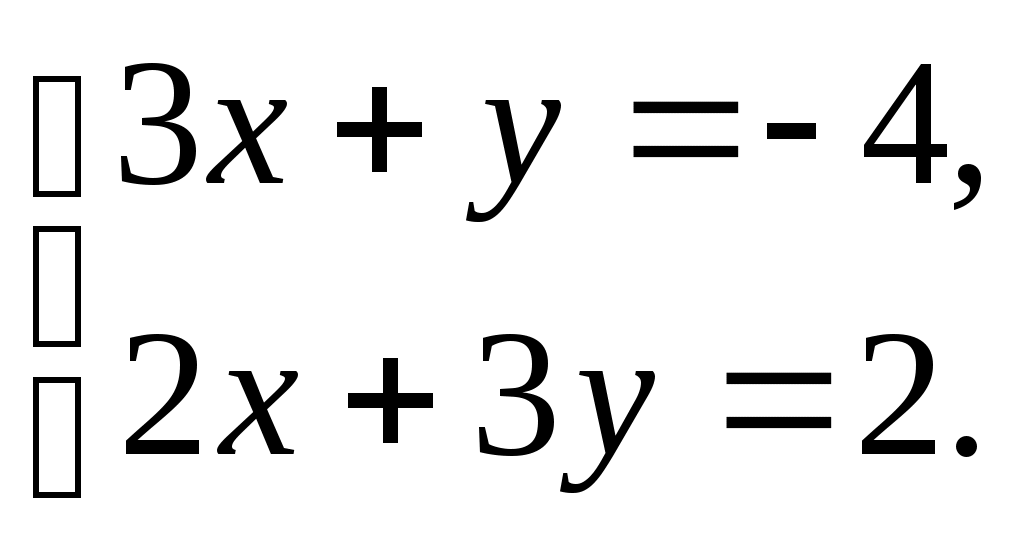
-
(1 балл) Найдите значение выражения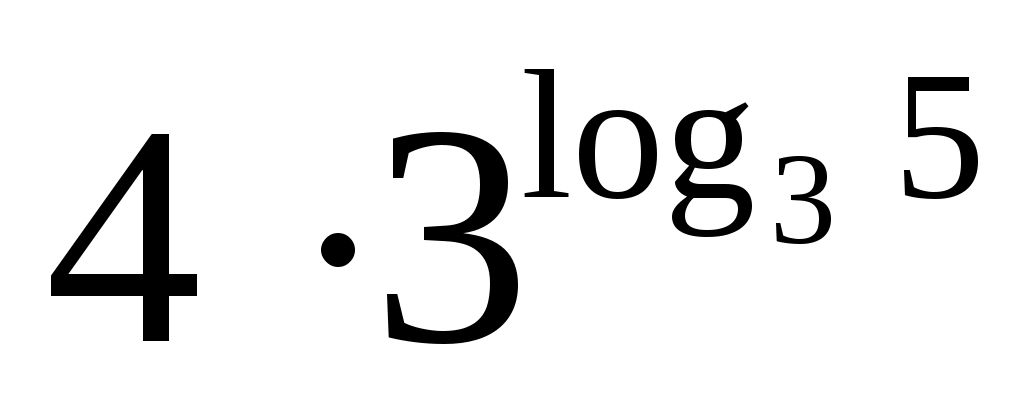 .
.
При выполнении заданий 6-9, используя график функции
-
(1 балл) Область определения функции. -
(1 балл) Четность, нечетность функции. -
(1 балл) Монотонность функции. -
(1 балл) Нули функции.
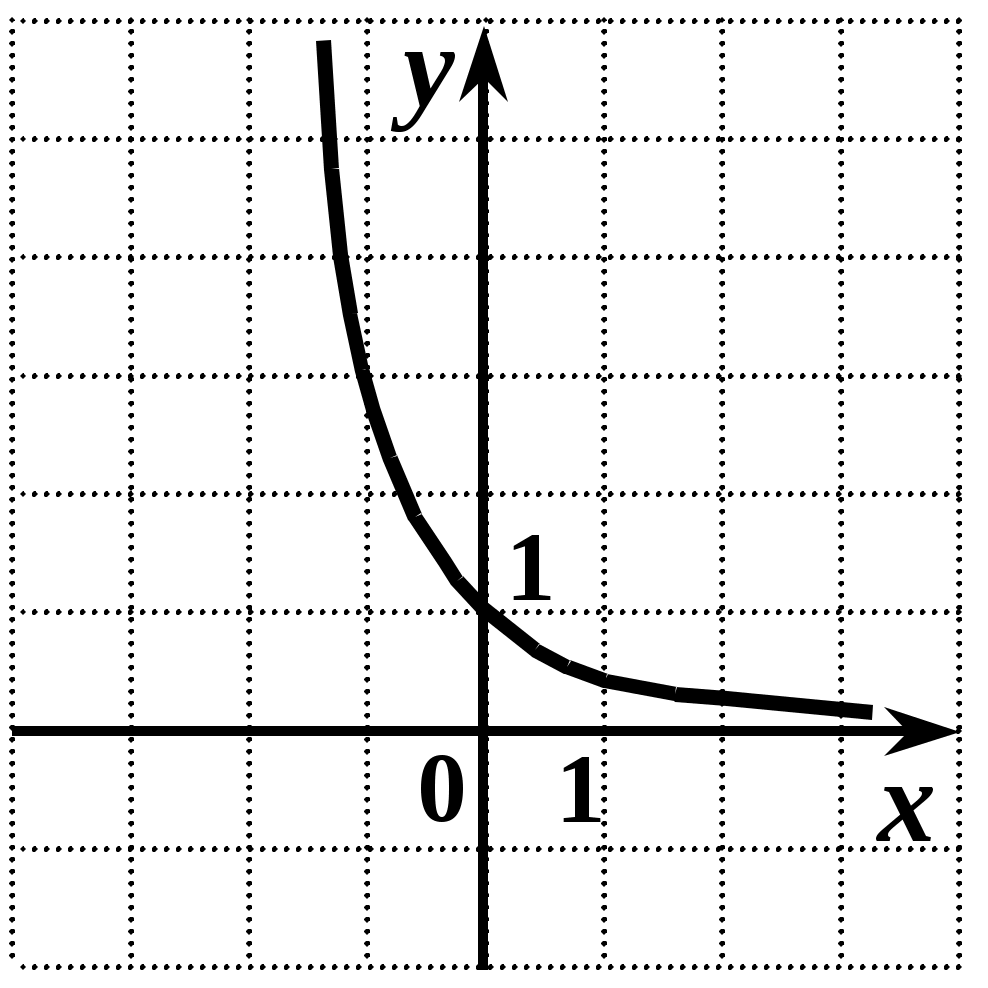
При выполнении заданий 10-15 укажите ход решения и запишите полученный ответ.
-
(1 балл) Найдите значение , если известно, что
, если известно, что 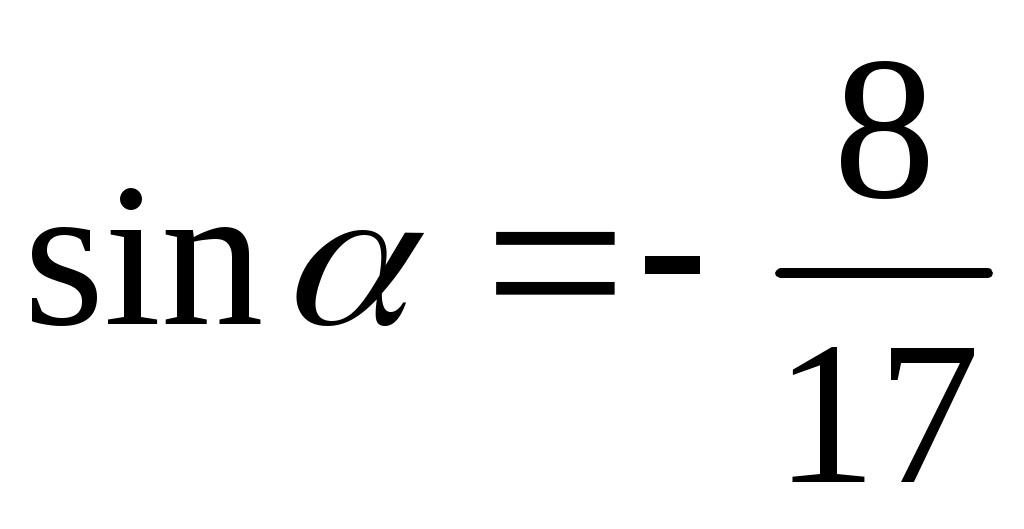 и
и  четверти.
четверти. -
(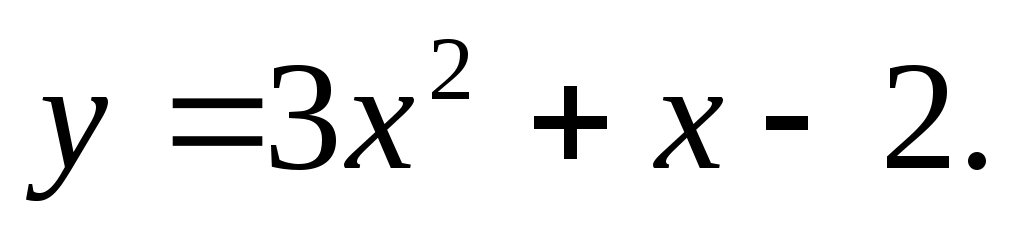 1 балл) Найдите нули функции
1 балл) Найдите нули функции -
(1 балл) Найти производную функции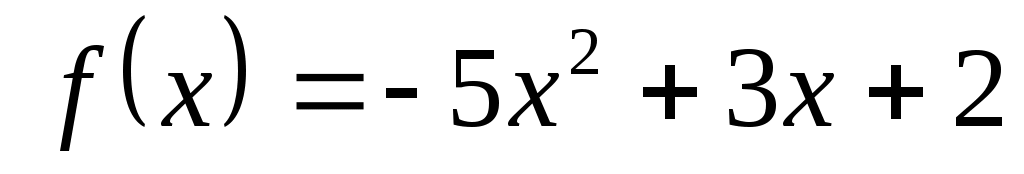
-
(1 балл) В прямоугольном параллелепипеде известно, что
известно, что  ,
, 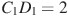 ,
,  . Найдите длину ребра .
. Найдите длину ребра .
14) (1 балл) Решите уравнение sin x =
15) (1 балл) Найдите область определения функции
Дополнительная часть
При выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Из 100 билетов выигрышными являются 15. Какова вероятность того, что среди 6-ти билетов, взятых на удачу, будет два выигрышных?
17) (3 балла) Найдите корни уравнения
18) (3 балла) Апофема правильной четырехугольной пирамиды равна 5 м, высота пирамиды равна 4 м. Найти объём и площадь полной поверхности пирамиды.