ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 78
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Форма титульного листа расчетно-графической работы
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение
высшего образования
«Северный (Арктический) федеральный университет имени М.В. Ломоносова»
Высшая Школа Энергетики, Нефти и Газа
(наименование высшей школы / филиала / института / колледжа)
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
| По дисциплине/междисциплинарному курсу/модулю | Методы Анализа Данных | | ||
| | | |||
| | | |||
| На тему:Вариант 5 | | |||
| | | |||
| | Выполнил (-а) обучающийся (-аяся): Дьячков Сергей Андреевич | ||||
| | (Ф.И.О.) | ||||
| | Направление подготовки / специальность: Теплоэнергетика и теплотехника 13.03.01 | ||||
| | (код и наименование) | ||||
| | Курс: 2 | ||||
| | Группа: 111113 | ||||
| | Руководитель: Зеленина Лариса Ивановна | ||||
| | (Ф.И.О. руководителя, должность / уч. степень / звание) | ||||
| Отметка о зачете | | | | | |
| | | (отметка прописью) | | (дата) | |
| Руководитель | | | | Зеленина Л. И. | |
| | | (подпись руководителя) | | (инициалы, фамилия) | |
Архангельск 2023
ЛИСТ ДЛЯ ЗАМЕЧАНИЙ
ОГЛАВЛЕНИЕ
ЛИСТ ДЛЯ ЗАМЕЧАНИЙ 2
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 4
ЗАДАНИЕ 10
ЗАДАЧА 1 12
ЗАДАЧА 2 12
РЕШЕНИЕ 14
Задача 1 14
Задача 2 28
ЗАКЛЮЧЕНИЕ 32
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 34
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
5.Теоретические основы выборочного метода. Генеральная и выборочная совокупности. Способы формирования выборочных совокупностей.
Теория выборочного наблюдения базируется на статистических закономерностях, которые формируются и обнаруживаются в массовых явлениях и процессах. Это свойство закономерностей получило название закона больших чисел. Математической основой закона больших чисел, да и статистической науки в целом, служит теория вероятностей. Без применения знаний выборочного наблюдения и выборочной совокупности невозможно оценить масштабные клинические исследования, наблюдения, спрогнозировать различные явления и обрабатывать первичные данные.
Выборочный метод - это наиболее совершенная с научной точки зрения разновидность несплошного статистического наблюдения на основе статистической индукции, при котором характеристики всей статистической (генеральной) совокупностью (N) получаются в результате изучения некоторой ее части (n), отобранной с соблюдением определенных правил (на основе случайного отбора) и поэтому являющейся репрезентативной, т.е. репрезентативной и достоверной.
Репрезентативность — это способность выборочной совокупности как количественно, так и качественно отражать свойства генеральной совокупности. Количественная репрезентативность достигается достаточностью числа наблюдений, качественная — соответствием признаков единиц наблюдения в выборочной и генеральной совокупностях.
Теория выборочных обследований базируется на принципе, исключающем субъективность и тенденциозность поведения отбора единиц для их последующего изучения по заранее разработанной программе. Она исходит из следующих положений:
− выбор той или иной конкретной единицы для обследования должен быть независим от воли, субъективного подхода лица, производящего отбор;
− выбор должен быть независим от значений изучаемых статистических характеристик (показателей), которыми обладают отдельные единицы совокупности;
− процесс отбора должен быть организован так, чтобы все единицы совокупности имели равные шансы, равные вероятности быть отобранными
Генеральная совокупность — вся изучаемая выборочным методом статистическая совокупность объектов и/или явлений общественной жизни (единиц отбора), имеющих общие качественные признаки или количественные переменные.
Методология выборочного статистического исследования включает три элемента:
1) Выборочное наблюдение – на этом этапе собираются сведения о каждой единице совокупности, сформированные на основе того или иного способа отбора из общей совокупности единиц.
2) Сводка и группировка полученных на основе выборочного обследования материалов – на этом этапе сведения, относящиеся к каждой единице выборочной совокупности, объединяются в группы и подгруппы по заранее разработанной программе.
3) Собранные и сгруппированные данные анализируются и распространяются на всю изучаемую совокупность, при этом рассчитываются абсолютные, относительные, средние показатели и т.д.
Выборочная совокупность - совокупность единиц, которая отобрана из генеральной совокупности и подвергнута наблюдению (регистрации интересующих нас признаков).
Простая случайная выборка регистрируются все элементы генеральной совокупности, затем случайным образом происходит отбор выборочной совокупности. Любой элемент генеральной совокупности имеет равный и независимый шанс быть выбранным в качестве части выборочной совокупности.
- Низкий риск систематической ошибки.
- Требуется много времени для получения выборки
- Отбор по первой букве фамилии
- Расслоенная случайная выборка
- Отбор участников случайным образом из двух или более групп, на которые предварительно была разделена генеральная совокупность
- Высокая репрезентативность.
- Низкий риск систематической ошибки.
- Требуется много времени для получения выборки.
- Необходимо знание основной структуры генеральной совокупности
- Педагогические работники всех образовательных учреждений: администрация, учителя, а затем отбирается случайным образом (по первой букве фамилии)
Выборка путем разбиения на группы – это многоэтапный процесс взятия выборки, при котором сначала отбираются большие группы, затем следует отбор все более мелких единиц выборки. Эффективный способ получения большой выборки, если нельзя использовать единицы генеральной совокупности.
Систематическая выборка – вероятностный метод выборки, в соответствии с которым сначала задают произвольную отправную точку, а затем из основы выборочного наблюдения последовательно выбирают каждый i-й элемент.
15. КЛАССИЧЕСКАЯ МОДЕЛЬ РЕГРЕССИОННОГО АНАЛИЗА, УСЛОВИЯ ЕЕ КОРРЕКТНОГО ПРИМЕНЕНИЯ.
Применяя методы регрессионного анализа, следует подчеркнуть важность условий, которые должны обеспечивать корректность сделанных выводов.
Теоретическая модель классической парной линейной регрессии (зависимость между переменными в генеральной совокупности), или классическая линейная регрессионная модель (КЛРМ), имеет вид:
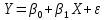
где X рассматривается как неслучайная переменная, a Y и в — как случайные величины.
Индивидуальные значения г/, выражаются по формуле
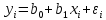
где i изменяется от 1 до п.
Для определения Р0 и pi необходимо знать и использовать все значения переменных X и Y генеральной совокупности, что практически невозможно. Методами регрессионного анализа возможно получить лишь их оценки на основании выборочных (экспериментальных) данных:
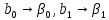
В классическом регрессионном анализе необходимо выполнение следующих предположений:
1.
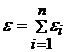 , где n число наблюдений. Величина
, где n число наблюдений. Величина также случайная величина с распределением того же вида, что и
2.
3. Значения случайной величины
4. Случайная величина
5. Матрица регрессоров MF (5) не случайна.
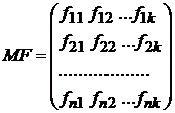 (5)
(5)Где
| | |
Все регрессоры
6. На значения параметров модели (4)