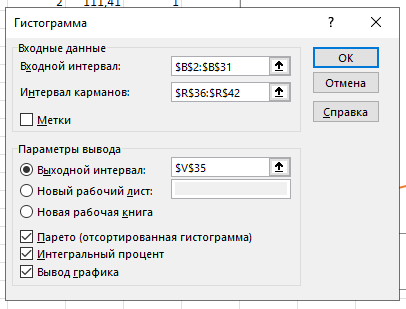
Рисунок 3 − Заполнение диалогового окна гистограмма



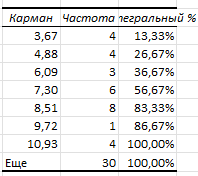
Рисунок 4 − Этапы построения интервального вариационного ряда с

помощью инструмента гистограмма


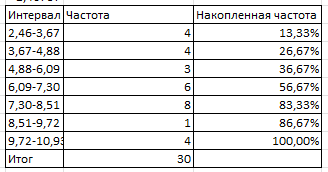
Рисунок 5 − Интервальный вариационный ряд признака Х



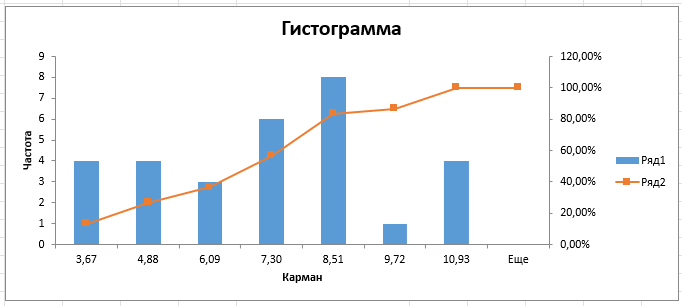
Рисунок 6 − Гистограмма и полигон распределения признака Х

2. Определим статистические характеристики рядов распределения. Для дискретного вариационного ряда находим их с помощью инструмента Анализа данных Описательная статистика



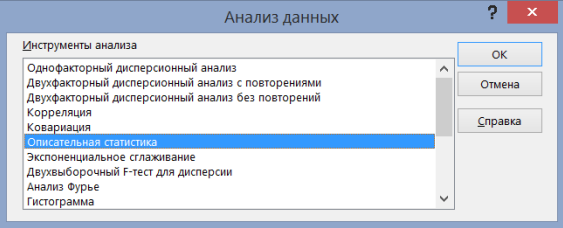
Рисунок 7 − Вызов инструментов Анализа данных Описательная статистика



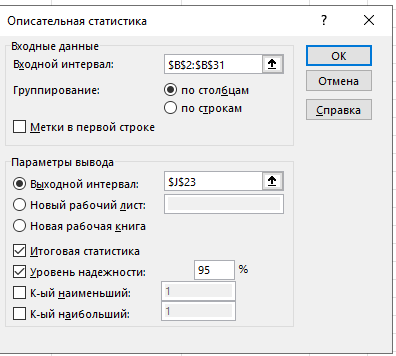
Рисунок 8 − Заполнение диалогового окна описательная статистика



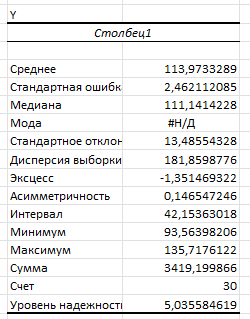
Рисунок 9 − Результаты описательной статистики

Среднее значение зависимого признака Yравно:

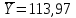
Моды – нет, так как все значения зависимого признака Yвстречаются по одному разу в совокупности.

Медиана:

Me 111,141.

Половина значений зависимой переменной меньше 111,141, а другая половина больше 111,141.

Размах вариации:

R  42,15.

Наибольшее значение признака Yпревышает наименьшее на 42,15.

Для вычисления среднего линейного отклонения используем функцию Excel СРОТКЛ, для вычисления выборочной дисперсии – функцию ДИСПР, а для вычисления среднего квадратического отклонения используем функцию

---

СТАНДОТКЛОНП (рисунок 10).



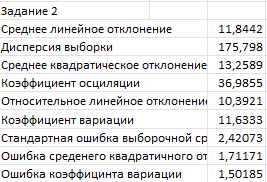
Рисунок 10 − Результаты вычисления показателей вариации

Среднее линейное отклонение:

d 11,844.

Дисперсия:

 ²  175,798.

Среднее квадратическое отклонение:

  13,26.

Каждое значение признака Yв среднем отличается от среднего значения на 13,26.

Коэффициент вариации:



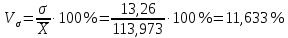
Найдем коэффициент асимметрии, вычислим с помощью функции СКОС в Excel:



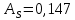
Так как 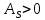, то асимметрия правосторонняя (распределение смещено вправо). Значение коэффициента по модулю меньше, чем 0,25, значит асимметрия незначительная.
Найдем коэффициент эксцесса с помощью функции ЭКСЦЕСС в Excel:



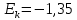
Эмпирическое распределение является более низким и пологим (в данных наблюдается меньше выбросов, чем в нормальном распределении, относительно сглаженное распределение).

Так как коэффициент вариации V_ნ ˂ 33%, то совокупность значений признака Y однородная, вариация значений признака Y не сильная.

Для интервального вариационного ряда признака Х проведем дополнительные вычисления.

№	Интервал	Середина интервала,	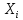Частота,	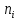	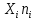Накопленная частота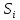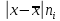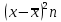
1	2,46 − 3,67	3,06	4	12,24	4	14,36	51,54
2	3,67 − 4,88	4,27	4	17,08	8	9,52	22,65
3	4,88 − 6,09	5,48	3	16,44	11	3,51	4,10
4	6,09 − 7,30	6,69	6	40,14	17	0,24	0,01
5	7,30 − 8,51	7,9	8	63,2	25	10,00	12,51
6	8,51 − 9,72	9,11	1	9,11	26	2,46	6,05
7	9,72 - 10,93	10,32	4	41,28	30	14,68	53,89
Итог		−	30	199,49	−	37,63	150,75

---

Таблица 4 − Промежуточные вычисления
Среднее значение признака Х:



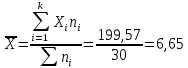
Мода:


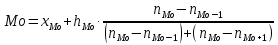
где х_мо– нижняя граница модального интервала;

h_мо– величина модального интервала;

n_мо,n_мо-1,n_мо+1– частоты в модальном, предыдущем и следующим за модальным интервалах (соответственно).
Модальным интервалом построенного ряда является интервал 7,30 –8,51, т.к. он имеет наибольшую частоту (n₅=8)



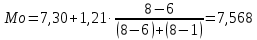
Наиболее часто встречающееся значение признака Х равно 7,57.

Медиана:



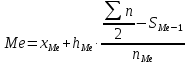
где х_ме– нижняя граница медианного интервала;

h_ме– величина медианного интервала;

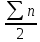– половина от общей численности частот;

S_ме-1 – накопленная частота до начала медианного интервала;

n_ме– частота медианного интервала.

Медианным интервалом является интервал 6,09–7,30, т. к. именно в этом интервале накопленная частота S₄=17 впервые превышает полусумму всех частот .



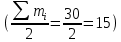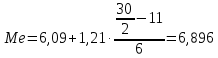
Половина значений признака Х меньше 6,896, и другая половина значений признака Х больше 6,896.

Размах вариации:

---

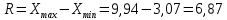
Наибольшее значение признака Х превышает наименьшее на 6,87

Среднее линейное отклонение:


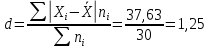
Дисперсия:



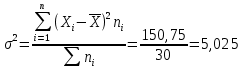
Среднее квадратическое отклонение:



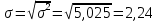
Каждое значение признака Хв среднем отличается от среднего значения на 2,24.

Коэффициент осцилляции:



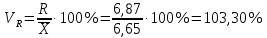
Относительное линейное отклонение:



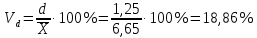
Коэффициент вариации:



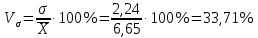
Найдем коэффициент асимметрии, вычислим с помощью функции СКОС в Excel:



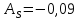
Так как 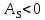, то асимметрия левосторонняя (распределение смещено влево). Значение коэффициента по модулю меньше, чем 0,25, значит асимметрия незначительная.

Найдем коэффициент эксцесса с помощью функции ЭКСЦЕСС в Excel:



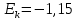
Эмпирическое распределение является более низким и пологим (в данных наблюдается меньше выбросов, чем в нормальном распределении, относительно сглаженное распределение).

Так как коэффициент вариации V_ნ ˃ 33%, то совокупность значений признака X неоднородная, вариация значений признака X сильная.
3. С помощью критерия Пирсона проверим гипотезу о нормальном распределении случайной величины Х.

Критерий согласия Пирсона определим по формуле:



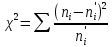
где – эмпирические частоты;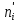

– теоретические частоты;

Теоретические расчеты определяем следующим образом:



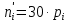
Где 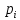– теоретические вероятности попадания в интервалы группировки :

---

Оформим вычисления в таблице 5

Таблица 5 – Промежуточные вычисления

№
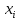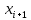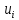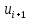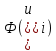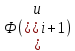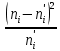1	2,46	3,67	4	-1,87	-1,33	-0,50	-0,41	0,09	2,76	0,56
2	3,67	4,88	4	-1,33	-0,79	-0,41	-0,29	0,12	3,69	0,03
3	4,88	6,09	3	-0,79	-0,25	-0,29	-0,10	0,19	5,59	1,20
4	6,09	7,30	6	-0,25	0,29	-0,10	0,11	0,21	6,38	0,02
5	7,30	8,51	8	0,29	0,83	0,11	0,30	0,18	5,48	1,16
6	8,51	9,72	1	0,83	1,37	0,30	0,41	0,12	3,54	1,82
7	9,72	10,93	4	1,37	1,91	0,41	0,50	0,09	2,56	0,81
Итог			30					1,00	30	5,60

---

Смотрите также файлы

• Определите преимущества и недостатки использования стратегической ориентации на проектную форму организации и оплаты труда производственного персонала, заполнив для этого соответствующие графы таблицы.docx

• Дипломной работы Система управления логистическими процессами на предприятии Введение.docx

• 1. Что такое сенсорные эталоны и какова их роль в познавательном развитии ребенкадошкольника.docx

• Методические указания к выполнению работы.docx

• История финансовой мысли, развитие теорий финансов в зарубежных странах ив России Теория финансов.pdf