ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 80
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Получили наблюдаемое значение критерия Пирсона:
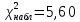
Табличное значение критерия Пирсона при уровне значимости
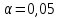составляет: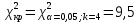
Где
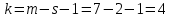
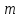– число интервалов;
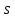– число параметров теоретического закона распределения;Расчетное значение критерия Пирсона меньше табличного
(
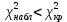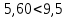), следовательно, случайная величина X распределена по нормальному закону.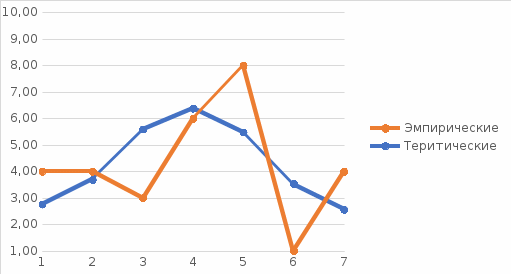
Рисунок 11 − Нормальная кривая по эмпирическим и теоретическим данным
4. Выполним статистическую оценку (точечную и интервальную) параметров распределения.
Стандартная ошибка выборочной средней:
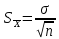
Ошибка среднего квадратического отклонения:
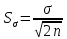
Ошибка коэффициента вариации:
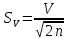
Для переменной Y получаем:
.
.
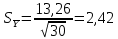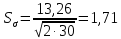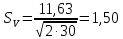.Для переменной Х по интервальному ряду получим:
.
.
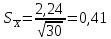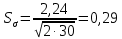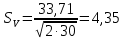.Оценим достоверность выборочной средней, среднего квадратического отклонения и коэффициент вариации по t-критерию Стьюдента.
Доверительный интервал для среднего значения определяется следующим образом:
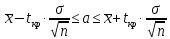
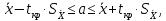
где tкр
– коэффициент доверия
Для доверительной вероятности 0,95 по интегральной таблице Лапласа
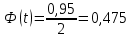он равен: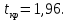 
Для переменной Y получим:
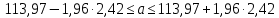
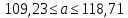
C вероятностью 0,95 среднее значение показателя Y в генеральной совокупности будет находиться в пределах от 109,23 до 118,71.
Для переменной Х по интервальному ряду:
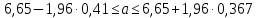
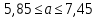
C вероятностью 0,95 среднее значение показателя Х в генеральной совокупности будет находиться в пределах от 5,85 до 7,45.
Доверительный интервал среднего квадратического отклонения определяется следующим образом:
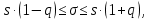
где s – исправленное среднее квадратическое отклонение;
q – находится по таблице.
Для уровня значимости 0,05 и n = 30: q = 0,28.
Для переменной Y:
S = 13,49
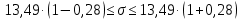
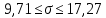
C вероятностью 0,95 среднее квадратическое отклонение показателя Y в генеральной совокупности будет находиться в пределах от 9,71 до 17,27.
Для переменной Х по интервальному ряду:
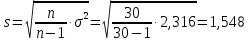
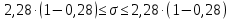
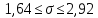
C вероятностью 0,95 среднее квадратическое отклонение показателя Х в генеральной совокупности будет находиться в пределах от 1,64 до 2,92.
Задача 2
1. Построим поле корреляции (рисунок 12).
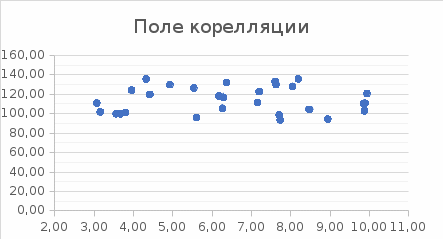
Рисунок 12 – Поле корреляции
Согласно полю корреляции, связь между признаками отсутствует.
2. Построим линейную трендовую модель с помощью инструмента Анализ данных Регрессия в Excel.
Рисунок 13 − Вызов инструментов Анализа данных Регрессия
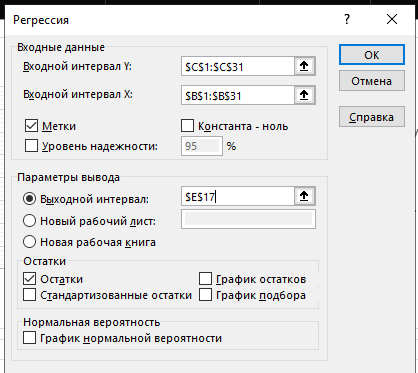
Рисунок 14 − Заполнение диалогового окна инструмента Регрессия
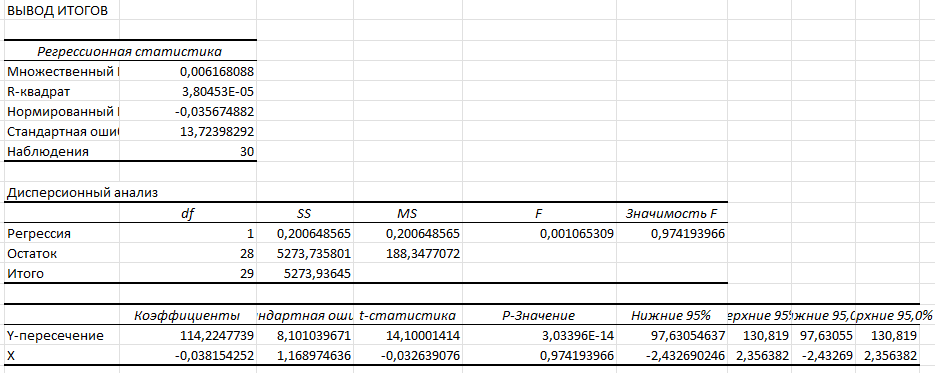
Рисунок 15 − Результаты регрессионного анализа
Получили уравнение линейной регрессии:
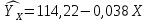
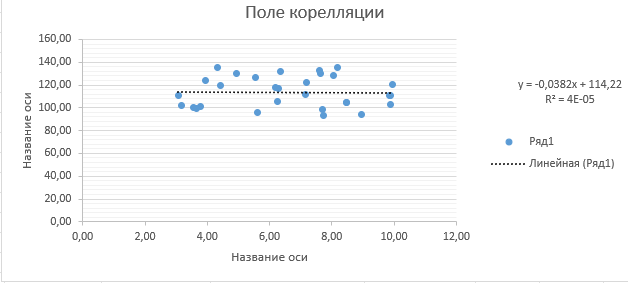
Рисунок 16 – Линейная модель
Коэффициент детерминации равен:
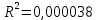
0,0038% вариации зависимого признака Y объясняется вариацией независимого признака Х.
Коэффициент корреляции определим с помощью функции КОРРЕЛ в Excel:
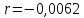
Корреляция слабая
4. Средний коэффициент эластичности:
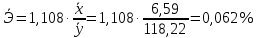
При увеличении признака Х на 1% от среднего значения признак Y в среднем увеличивается на 0,062%.
5. Средняя ошибка аппроксимации определяется по формуле:
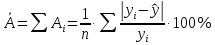
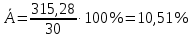
В среднем расчётные значения отклоняются от фактических на 10,51%, что говорит о приемлемом качестве модели.
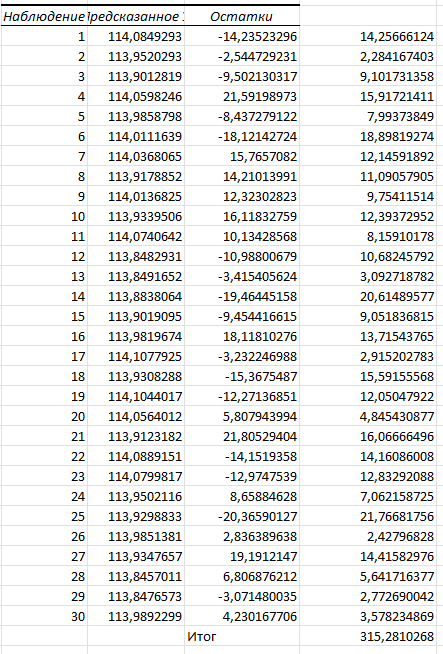
Рисунок 17 − Расчет средней ошибки аппроксимации
6. Оценим статистическую значимость параметров регрессии и уравнения регрессии в целом.
F-критерий Фишера для уравнения регрессии в целом (рисунок 15) равен:
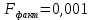
Критическое значение F-критерия при уровне значимости
и степенях свободы: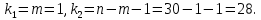
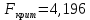(рисунок 18)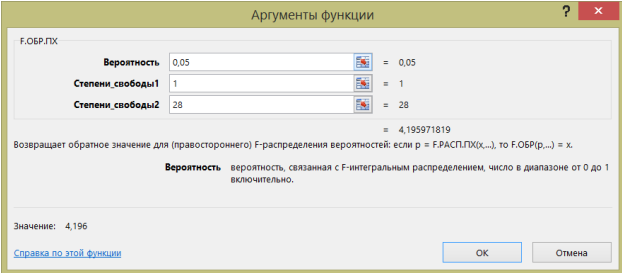
Рисунок 18 − Определение критического значения F-критерия Фишера
Так как Fфакт < Fкрит, то линейное уравнение регрессии не является значимым.
t-критерий Стьюдента для параметров (рисунок 15):
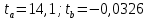
Критическое значение t-критерия при уровне значимости
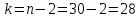состовляет:
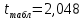(рисунок 19)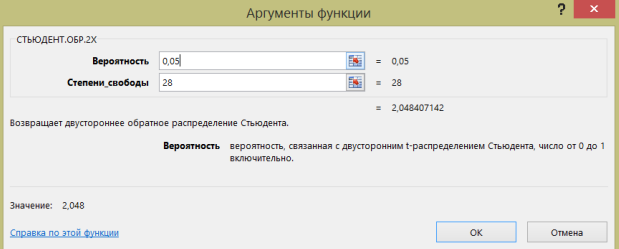
Рисунок 19 − Определение критического значения t-критерия Стьюдента
Так как tа>tтабл, то параметр a является значимым, а так как tb
ЗАКЛЮЧЕНИЕ
В первом задании рассматривается применение математических и статистических методов при анализе данных. Дискретная и вариационная последовательности основаны на зависимости и независимости соответственно. Дана оценка статистических характеристик последовательности распределения. Построена нормальная кривая и проверена гипотезу о нормальном распределении. Статистически оценены параметры распределения. Приводятся объяснения полученных результатов и делаются выводы.
Во втором задании был проведен корреляционный и регрессионный анализ на основе имеющихся данных. Установлено поле корреляции и выдвинута гипотеза о приближенном типе функции. Устанавливается линейная трендовая модель и определяются коэффициент корреляции и коэффициент детерминации.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1) Клячкин, Владимир Николаевич Сборник заданий по статистическим методам анализа данных : учебное пособие / В. Н. Клячкин, Ю. Е. Кувайскова, В. А. Алексеева. – Ульяновск : УлГТУ, 2016. – 123 с.— (Высшее образование). — ISBN 978-5-9795-1582-3. — Текст : электронный // — http://lib.ulstu.ru/venec/disk/2016/207.pdf (дата обращения: 08.05.2023).
1 2 3