ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 81
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
7. Ранг матрицы MF должен быть равен числу коэффициентов (регрессоров) модели 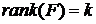 , где k – число различных регрессоров. Нарушение данного условия может быть вызвано в случае, когда число проведенных опытов меньше числа коэффициентов (
, где k – число различных регрессоров. Нарушение данного условия может быть вызвано в случае, когда число проведенных опытов меньше числа коэффициентов (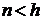 ), либо определено для ситуации (
), либо определено для ситуации (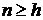 ), что между некоторыми столбцами матрицы MF существовала линейная зависимость.
), что между некоторыми столбцами матрицы MF существовала линейная зависимость.
Интерпретация моделей регрессии осуществляется методами той отрасли знаний, к которой относится исследуемое явление. Но всякая интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков.
Чем больше абсолютное значение коэффициента регрессии, тем значительнее влияние факторного признака на результативный признак.
Знак коэффициента регрессии говорит о характере влияния на результативный признак. Если коэффициент регрессии имеет знак плюс, то с увеличением фактора результатный признак возрастает. Если коэффициент регрессии имеет знак минус, то с его увеличением результативный признак уменьшается.
ЗАДАНИЕ
Таблица 1 – Исходные данные
ЗАДАЧА 1
Построить по зависимому признаку Y дискретный вариационный ряд, по независимому признаку Х –интервальный вариационный ряд. Построить полигон и гистограмму.
2.Оценить статистические характеристики рядов распределения.
2.1. Показатели центра распределения: средняя, мода, медиана
2.2. Показатели вариации признака: размах вариации, дисперсия, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии, коэффициент эксцесса.
3.Построить нормальную кривую по эмпирическим и теоретическим данным. На основе одного из критериев согласия Пирсона проверить гипотезу о законе нормального распределения.
4.Выполнить статистическую оценку (точечную и интервальную) параметров распределения:
4.1. определить ошибку выборки: стандартную ошибку выборочной средней, ошибку среднего квадратического отклонения, ошибку коэффициента вариации
4.2. оценить достоверность выборочной средней, среднего квадратического отклонения и коэффициент вариации по t-критерию Стьюдента.
Выполнить интерпретацию результатов, сделать вывод.
ЗАДАЧА 2
На основе имеющихся данных выполнить корреляционно –регрессионный анализ.
1.Построить поле корреляции, выдвинуть гипотезу о типе аппроксимирующей функции
2.Построить линейную трендовую модель.
3.Дляпостроенной модели определить коэффициент корреляции и коэффициент детерминации.
4.Дляпостроенной модели дать сравнительную оценку силы связи фактора с результатом с помощью среднего коэффициента эластичности
5.Дляпостроенной модели оценить качество построенных моделей с помощью средней ошибки аппроксимации.
6.Дляпостроенной модели оценить статистическую значимость параметров регрессии и уравнения регрессии в целом.
7. На основе пунктов 2–6 сделать вывод о качестве и точности построенной модели, выполнить прогноз среднего значения показателя Y при уровне значимости α=0,1, если прогнозное значение фактора X составляет 80 % от его максимального значения.
РЕШЕНИЕ
Задача 1
1. Построим по зависимому признаку Y дискретный вариационный ряд, для этого упорядочим данные по возрастанию и определим частоту повторений
каждой варианты.
Таблица 2– Дискретный вариационный ряд признака Y.
Строим полигон (рисунок 1)
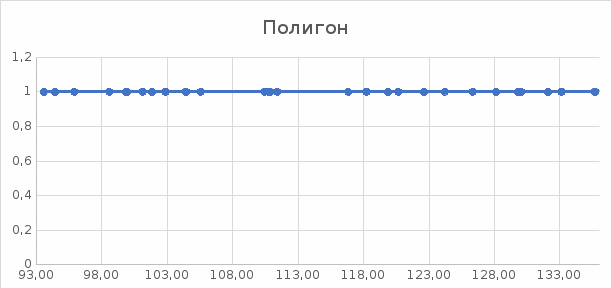
Рисунок 1 – Полигон распределения признака Y
Расположим значения независимого признака Х по возрастанию.
Таблица 3 – Значения признака Хпо возрастанию
Построим интервальный вариационный ряд независимого признака Х
средствами инструмента Гистограмма в Excel
Рисунок 2 − Вызов инструментов анализа данных гистограмма
Интерпретация моделей регрессии осуществляется методами той отрасли знаний, к которой относится исследуемое явление. Но всякая интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков.
Чем больше абсолютное значение коэффициента регрессии, тем значительнее влияние факторного признака на результативный признак.
Знак коэффициента регрессии говорит о характере влияния на результативный признак. Если коэффициент регрессии имеет знак плюс, то с увеличением фактора результатный признак возрастает. Если коэффициент регрессии имеет знак минус, то с его увеличением результативный признак уменьшается.
ЗАДАНИЕ
Таблица 1 – Исходные данные
| № | Х | У |
| 1 | 3,67 | 99,85 |
| 2 | 7,15 | 111,41 |
| 3 | 8,48 | 104,40 |
| 4 | 4,32 | 135,65 |
| 5 | 6,26 | 105,55 |
| 6 | 5,60 | 95,89 |
| 7 | 4,93 | 129,80 |
| 8 | 8,04 | 128,13 |
| 9 | 5,53 | 126,34 |
| 10 | 7,62 | 130,05 |
| 11 | 3,95 | 124,21 |
| 12 | 9,87 | 102,86 |
| 13 | 9,84 | 110,43 |
| 14 | 8,94 | 94,42 |
| 15 | 8,46 | 104,45 |
| 16 | 6,36 | 132,10 |
| 17 | 3,07 | 110,88 |
| 18 | 7,70 | 98,56 |
| 19 | 3,15 | 101,83 |
| 20 | 4,41 | 119,86 |
| 21 | 8,19 | 135,72 |
| 22 | 3,56 | 99,94 |
| 23 | 3,79 | 101,11 |
| 24 | 7,20 | 122,61 |
| 25 | 7,73 | 93,56 |
| 26 | 6,28 | 116,82 |
| 27 | 7,60 | 133,13 |
| 28 | 9,94 | 120,65 |
| 29 | 9,88 | 110,78 |
| 30 | 6,17 | 118,22 |
ЗАДАЧА 1
Построить по зависимому признаку Y дискретный вариационный ряд, по независимому признаку Х –интервальный вариационный ряд. Построить полигон и гистограмму.
2.Оценить статистические характеристики рядов распределения.
2.1. Показатели центра распределения: средняя, мода, медиана
2.2. Показатели вариации признака: размах вариации, дисперсия, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии, коэффициент эксцесса.
3.Построить нормальную кривую по эмпирическим и теоретическим данным. На основе одного из критериев согласия Пирсона проверить гипотезу о законе нормального распределения.
4.Выполнить статистическую оценку (точечную и интервальную) параметров распределения:
4.1. определить ошибку выборки: стандартную ошибку выборочной средней, ошибку среднего квадратического отклонения, ошибку коэффициента вариации
4.2. оценить достоверность выборочной средней, среднего квадратического отклонения и коэффициент вариации по t-критерию Стьюдента.
Выполнить интерпретацию результатов, сделать вывод.
ЗАДАЧА 2
На основе имеющихся данных выполнить корреляционно –регрессионный анализ.
1.Построить поле корреляции, выдвинуть гипотезу о типе аппроксимирующей функции
2.Построить линейную трендовую модель.
3.Дляпостроенной модели определить коэффициент корреляции и коэффициент детерминации.
4.Дляпостроенной модели дать сравнительную оценку силы связи фактора с результатом с помощью среднего коэффициента эластичности
5.Дляпостроенной модели оценить качество построенных моделей с помощью средней ошибки аппроксимации.
6.Дляпостроенной модели оценить статистическую значимость параметров регрессии и уравнения регрессии в целом.
7. На основе пунктов 2–6 сделать вывод о качестве и точности построенной модели, выполнить прогноз среднего значения показателя Y при уровне значимости α=0,1, если прогнозное значение фактора X составляет 80 % от его максимального значения.
РЕШЕНИЕ
Задача 1
1. Построим по зависимому признаку Y дискретный вариационный ряд, для этого упорядочим данные по возрастанию и определим частоту повторений
каждой варианты.
Таблица 2– Дискретный вариационный ряд признака Y.
| № п/п | Y | ni |
| 25 | 93,56 | 1 |
| 14 | 94,42 | 1 |
| 6 | 95,89 | 1 |
| 18 | 98,56 | 1 |
| 1 | 99,85 | 1 |
| 22 | 99,94 | 1 |
| 23 | 101,11 | 1 |
| 19 | 101,83 | 1 |
| 12 | 102,86 | 1 |
| 3 | 104,40 | 1 |
| 15 | 104,45 | 1 |
| 5 | 105,55 | 1 |
| 13 | 110,43 | 1 |
| 29 | 110,78 | 1 |
| 17 | 110,88 | 1 |
| 2 | 111,41 | 1 |
| 26 | 116,82 | 1 |
| 30 | 118,22 | 1 |
| 20 | 119,86 | 1 |
| 28 | 120,65 | 1 |
| 24 | 122,61 | 1 |
| 11 | 124,21 | 1 |
| 9 | 126,34 | 1 |
| 8 | 128,13 | 1 |
| 7 | 129,80 | 1 |
| 10 | 130,05 | 1 |
| 16 | 132,10 | 1 |
| 27 | 133,13 | 1 |
| 4 | 135,65 | 1 |
| 21 | 135,72 | 1 |
| Итого | 3419,20 | 30 |
Строим полигон (рисунок 1)

Рисунок 1 – Полигон распределения признака Y
Расположим значения независимого признака Х по возрастанию.
Таблица 3 – Значения признака Хпо возрастанию
| № п/п | X |
| 17 | 3,07 |
| 19 | 3,15 |
| 22 | 3,56 |
| 1 | 3,67 |
| 23 | 3,79 |
| 11 | 3,95 |
| 4 | 4,32 |
| 20 | 4,41 |
| 7 | 4,93 |
| 9 | 5,53 |
| 6 | 5,60 |
| 30 | 6,17 |
| 5 | 6,26 |
| 26 | 6,28 |
| 16 | 6,36 |
| 2 | 7,15 |
| 24 | 7,20 |
| 27 | 7,60 |
| 10 | 7,62 |
| 18 | 7,70 |
| 25 | 7,73 |
| 8 | 8,04 |
| 21 | 8,19 |
| 15 | 8,46 |
| 3 | 8,48 |
| 14 | 8,94 |
| 13 | 9,84 |
| 12 | 9,87 |
| 29 | 9,88 |
| 28 | 9,94 |
Построим интервальный вариационный ряд независимого признака Х
средствами инструмента Гистограмма в Excel

Рисунок 2 − Вызов инструментов анализа данных гистограмма