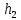ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 525
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
V = 5·10-3 м3. Охлаждающая жидкость – вода (βt = 150·10-6 1/°С).
Задача 1.8. Канистра вместимостью V= 20 л была доверху заполнена бензином, температура которого составляла t1 = 20˚С. Какое избыточное давление создастся в канистре в случае хранения ее в боксе при температуре t2 = 35˚С? Деформацией канистры пренебречь.
Задача 1.9. Определить падение давления масла в напорной линии гидропривода вместимостью V = 0, 015 м3, если утечки масла ΔV = 5·10-3 м3, а коэффициент объемного сжатия βр = 7,5·10-10 1/Па. Деформацией элементов гидропривода пренебречь.
Задача 1.10. Минеральное масло сжималось в стальной цилиндрической трубке. Пренебрегая деформацией трубки, определить коэффициент объемного сжатия βр и модуль упругости масла Е, если ход поршня составил Δh = 3,7 мм, а давление жидкости возросло на Δр = 5 МПа, высота налива масла h = 1000 мм.
Задача 1.11. В системе охлаждения ДВС при температуре t1 = 10°C содержится V = 10 л воды. Определить объем воды, который дополнительно войдет в расширительный бачок при повышении температуры до t2 = 90°C.
Задача 1.12. Динамический коэффициент вязкости масла плотностью ρ = 900 кг/м3 при температуре t = 50°C составляет μ = 0,06 Па·с. Определить кинематический коэффициент вязкости масла.
Задача 1.13. Вязкость трансформаторного масла, определенная вискозиметром, составила 4°Е. Плотность масла ρ = 910 кг/м3. Определить кинематический и динамический коэффициенты вязкости масла.
Задача 1.14. При экспериментальном определении вязкости минерального масла вискозиметром получено: время истечения 200 см3 дистиллированной воды при температуре 20°С Тв = 51,2 с, время истечения 200 см3 масла Тм = 163,4 с. Определить кинематический коэффициент вязкости масла.
З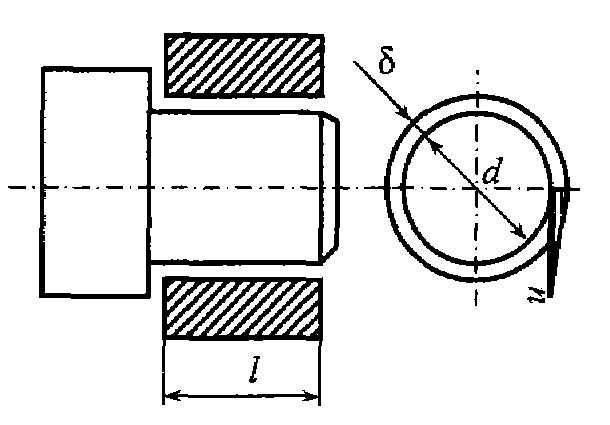
адача 1.15. Определить силу трения, затрачиваемую на преодоление трения в подшипнике при вращении вала. Частота вращения вала n= 10 с-1. Диаметр цапфы вала d= 40 мм, длинаl= 100 мм, толщина слоя смазки между цапфой и подшипником δ = 0,2 мм. Кинематический коэффициент вязкости масла ν = 0,8·10-4 м2/с, его плотность ρ = 920 кг/м3. Считать, что вал в подшипнике вращается соосно, а скорость движения жидкости в слое масла меняется по линейному закону.
З
адача 1.16. Определить мощность, затрачиваемую на преодоление трения в подшипнике при вращении вала (рис. к задаче В.15). Частота вращения валаn= 15 с-1. Диаметр цапфы вала d= 100 мм, длинаl= 120 мм, толщина слоя смазки между цапфой и подшипником δ = 0,15 мм. Кинематический коэффициент вязкости масла ν = 0,7·10-4 м2/с, его плотность ρ = 915 кг/м3. Считать, что вал в подшипнике вращается соосно, а скорость движения жидкости в слое масла меняется по линейному закону.
Задача 1.17. Кольцевая щель между двумя цилиндрами диаметрами D = 200 мм и d = 192 мм залита трансформаторным маслом при температуре t = 20°C. Внутренний цилиндр вращается равномерно с частотой n = 110 мин-1. Определить динамический μ и кинематический ν коэффициенты вязкости масла, если момент, приложенный к внутреннему цилиндру, М = 0,06 Н·м, а высота столба жидкости в щели между цилиндрами h = 100 мм. Трением основания внутреннего цилиндра пренебречь.
Задача 1.18. Кольцевая щель между двумя цилиндрами диаметрами d = 192 мм и D = 200 мм залита трансформаторным маслом ρ = 915 кг/м3. Внутренний цилиндр вращается равномерно с частотой n = 110 мин-1. Определить касательные напряжения в жидкости.
Задача 1.19. По металлическому стержню, установленному вертикально и смазанному минеральным маслом, скользит вниз равномерно под действием собственного веса втулка. Диаметр стержня d = 118 мм, внутренний диаметр втулки D = 120 мм, длина втулки l = 100 мм. Определить вес втулки при условии, что скорость движения втулки по стержню не должна превышать 0,6 м/с.
Задача 1.20. Определить ротационным вискозиметром вязкость жидкости плотностью ρ = 900 кг/м3. Вес груза G = 75 Н, диаметры цилиндра Dц = 250 мм, барабана Dб = 248 мм, шкива d = 200 мм. Глубина погружения барабана в жидкость lб = 250 мм. Время опускания грузаtгр = 10 с, путь lгр = 350 мм.
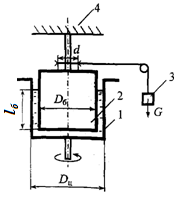
Примечание: Схема ротационного вискозиметра: в цилиндре 1 установлен барабан 2, вращающийся под действием опускающегося груза 3. Цилиндр закреплен на основании 4.
2. Гидростатика
Гидростатикой называется раздел гидравлики
, в котором рассматриваются законы равновесия жидкости и их практическое применение.
На жидкость действуют внешние силы, распределенные по ее массе (объемные) и по поверхности (поверхностные силы). К первым относятся силы тяготения, силы инерции, ко вторым - силы давления внутри жидкости и атмосферного давления на свободную поверхность, силы трения в движущейся жидкости. При воздействии внешних сил в жидкости возникает давление.
Давлениемназывается отношение силы, перпендикулярной поверхности, к площади, на которую действует сила.
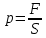
Если давление отсчитывают от абсолютного нуля, то его называют абсолютным (pабс.), если от условного нуля, за который принято атмосферное давление (ра.), то избыточным (манометрическим) (ризб.), т.е.
pабс.= ра.+ ризб.
Если давление в жидкости меньше атмосферного, подобное состояние называют вакуум (разрежение):
pвак.= ра.- рабс.
Единица измерения давления – Паскаль (Па), но наиболее удобными для практического использования являются кратные единицы: 1 кПа = 103 Па, 1 МПа = 106 Па. Наряду с этими используют и другие единицы измерения: бар, техническая атмосфера (ат), физическая атмосфера (атм), единица жидкосного столба (мм рт.ст., мм вод.ст.). Соотношения между единицами давления представлены в приложении 2.
Гидростатическое давление– давление в неподвижной жидкости. Гидростатическое давление обладает следующими свойствами.
10. В любой точке жидкости оно направлено перпендикулярно поверхности внутрь рассматриваемого объема жидкости.
20. Оно неизменно во всех направлениях.
30. Гидростатическое давление в точке зависит от ее координат в пространстве.
Уравнение, позволяющее находить гидростатическое давление в любой точке покоящейся жидкости при условии действия на нее только силы тяжести, называется основным уравнением гидростатики.
p =p0 + ρgh, (2.1)
где р0 – давление на свободной поверхности жидкости, которое передается всем точкам этой жидкости и по всем направлениям без изменения (закон Паскаля); ρ – плотность жидкости; g = 9,8 м/с2 – ускорение свободного падения;h– глубина расположения рассматриваемой точки.
Из основного уравнения гидростатики следует, что полная
сила давления жидкости на плоскую стенку равна произведению площади стенки S на гидростатическое давление рс в центре тяжести этой площади
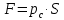
Центр давления – точка приложения силы давления от веса жидкости – располагается ниже центра тяжести или совпадает с последним в случае горизонтальной стенки.
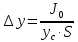
где J0 - момент инерции площади S, проходящей относительно центральной оси, перпендикулярной плоскости стенки;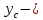
координата центра тяжести.
Сила давления жидкости на криволинейную стенку определяется как векторная сумма горизонтальной и вертикальной составляющих полной силы: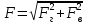
Горизонтальная составляющая численно равна силе давления на площадь вертикальной проекции стенки:
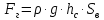
Вертикальная составляющая численно равна весу жидкости в объеме тела давления:
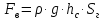
Телом давления называют объем жидкости, ограниченный данной криволинейной поверхностью, вертикальной поверхностью, проведенной через нижнюю образующую криволинейной поверхности, и свободной поверхностью жидкости.
Рекомендации к решению задач
1) выбрать поверхность равного давления (поверхность уровня) – любая горизонтальная плоскость на произвольной глубине;
2) рассмотреть на этой плоскости любые две точки и записать выражение для определения абсолютного давления в этих точках, используя основное уравнение гидростатики. При этом, необходимо обратить внимание на знак перед вторым членом правой части уравнения: знак «+» ставится в случае увеличения глубины (давление возрастает), «-» – при подъеме (давление уменьшается);
3) записать уравнение равенства давлений в точках, приравняв правые части записанных выражений;
4) из полученного уравнения выразить неизвестную величину.
1) составить уравнение сил, приложенных к некоторому подвижному телу (поршню);
2) записать формулы для нахождения каждой из сил, действующих на тело. При этом, давление со стороны жидкости нужно определить, используя основное уравнение гидростатики;
3) подставить полученные зависимости в уравнение равновесия сил и выразить неизвестную величину.
Примеры решения задач
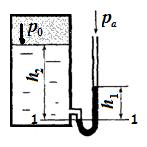
Пример 2.1. Определить абсолютное давление p0 на поверхности бензина в закрытом резервуаре, если показания ртутного пьезометра h1, а глубина h2. Значения плотности бензина ρб и ртути ρрт взять в табл.4.1 (приложение 4).
Решение:
Выбираем поверхность равного давления на уровне 1-1. Рассмотрим гидростатическое давление на этом уровне со стороны ртутного пьезометра и резервуара.
Давление в любой точке уровня 1-1 со стороны ртутного пьезометра согласно основному уравнению гидростатики
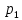= pа + 
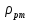g
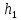
Давление со стороны резервуара
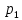= p0 + 
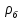g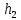
Задача 1.8. Канистра вместимостью V= 20 л была доверху заполнена бензином, температура которого составляла t1 = 20˚С. Какое избыточное давление создастся в канистре в случае хранения ее в боксе при температуре t2 = 35˚С? Деформацией канистры пренебречь.
Задача 1.9. Определить падение давления масла в напорной линии гидропривода вместимостью V = 0, 015 м3, если утечки масла ΔV = 5·10-3 м3, а коэффициент объемного сжатия βр = 7,5·10-10 1/Па. Деформацией элементов гидропривода пренебречь.
Задача 1.10. Минеральное масло сжималось в стальной цилиндрической трубке. Пренебрегая деформацией трубки, определить коэффициент объемного сжатия βр и модуль упругости масла Е, если ход поршня составил Δh = 3,7 мм, а давление жидкости возросло на Δр = 5 МПа, высота налива масла h = 1000 мм.
Задача 1.11. В системе охлаждения ДВС при температуре t1 = 10°C содержится V = 10 л воды. Определить объем воды, который дополнительно войдет в расширительный бачок при повышении температуры до t2 = 90°C.
Задача 1.12. Динамический коэффициент вязкости масла плотностью ρ = 900 кг/м3 при температуре t = 50°C составляет μ = 0,06 Па·с. Определить кинематический коэффициент вязкости масла.
Задача 1.13. Вязкость трансформаторного масла, определенная вискозиметром, составила 4°Е. Плотность масла ρ = 910 кг/м3. Определить кинематический и динамический коэффициенты вязкости масла.
Задача 1.14. При экспериментальном определении вязкости минерального масла вискозиметром получено: время истечения 200 см3 дистиллированной воды при температуре 20°С Тв = 51,2 с, время истечения 200 см3 масла Тм = 163,4 с. Определить кинематический коэффициент вязкости масла.
З
адача 1.15. Определить силу трения, затрачиваемую на преодоление трения в подшипнике при вращении вала. Частота вращения вала n= 10 с-1. Диаметр цапфы вала d= 40 мм, длинаl= 100 мм, толщина слоя смазки между цапфой и подшипником δ = 0,2 мм. Кинематический коэффициент вязкости масла ν = 0,8·10-4 м2/с, его плотность ρ = 920 кг/м3. Считать, что вал в подшипнике вращается соосно, а скорость движения жидкости в слое масла меняется по линейному закону.
З
адача 1.16. Определить мощность, затрачиваемую на преодоление трения в подшипнике при вращении вала (рис. к задаче В.15). Частота вращения валаn= 15 с-1. Диаметр цапфы вала d= 100 мм, длинаl= 120 мм, толщина слоя смазки между цапфой и подшипником δ = 0,15 мм. Кинематический коэффициент вязкости масла ν = 0,7·10-4 м2/с, его плотность ρ = 915 кг/м3. Считать, что вал в подшипнике вращается соосно, а скорость движения жидкости в слое масла меняется по линейному закону.Задача 1.17. Кольцевая щель между двумя цилиндрами диаметрами D = 200 мм и d = 192 мм залита трансформаторным маслом при температуре t = 20°C. Внутренний цилиндр вращается равномерно с частотой n = 110 мин-1. Определить динамический μ и кинематический ν коэффициенты вязкости масла, если момент, приложенный к внутреннему цилиндру, М = 0,06 Н·м, а высота столба жидкости в щели между цилиндрами h = 100 мм. Трением основания внутреннего цилиндра пренебречь.
Задача 1.18. Кольцевая щель между двумя цилиндрами диаметрами d = 192 мм и D = 200 мм залита трансформаторным маслом ρ = 915 кг/м3. Внутренний цилиндр вращается равномерно с частотой n = 110 мин-1. Определить касательные напряжения в жидкости.
Задача 1.19. По металлическому стержню, установленному вертикально и смазанному минеральным маслом, скользит вниз равномерно под действием собственного веса втулка. Диаметр стержня d = 118 мм, внутренний диаметр втулки D = 120 мм, длина втулки l = 100 мм. Определить вес втулки при условии, что скорость движения втулки по стержню не должна превышать 0,6 м/с.
Задача 1.20. Определить ротационным вискозиметром вязкость жидкости плотностью ρ = 900 кг/м3. Вес груза G = 75 Н, диаметры цилиндра Dц = 250 мм, барабана Dб = 248 мм, шкива d = 200 мм. Глубина погружения барабана в жидкость lб = 250 мм. Время опускания грузаtгр = 10 с, путь lгр = 350 мм.
Примечание: Схема ротационного вискозиметра: в цилиндре 1 установлен барабан 2, вращающийся под действием опускающегося груза 3. Цилиндр закреплен на основании 4.
2. Гидростатика
Гидростатикой называется раздел гидравлики
, в котором рассматриваются законы равновесия жидкости и их практическое применение.
На жидкость действуют внешние силы, распределенные по ее массе (объемные) и по поверхности (поверхностные силы). К первым относятся силы тяготения, силы инерции, ко вторым - силы давления внутри жидкости и атмосферного давления на свободную поверхность, силы трения в движущейся жидкости. При воздействии внешних сил в жидкости возникает давление.
Давлениемназывается отношение силы, перпендикулярной поверхности, к площади, на которую действует сила.
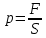
Если давление отсчитывают от абсолютного нуля, то его называют абсолютным (pабс.), если от условного нуля, за который принято атмосферное давление (ра.), то избыточным (манометрическим) (ризб.), т.е.
pабс.= ра.+ ризб.
Если давление в жидкости меньше атмосферного, подобное состояние называют вакуум (разрежение):
pвак.= ра.- рабс.
Единица измерения давления – Паскаль (Па), но наиболее удобными для практического использования являются кратные единицы: 1 кПа = 103 Па, 1 МПа = 106 Па. Наряду с этими используют и другие единицы измерения: бар, техническая атмосфера (ат), физическая атмосфера (атм), единица жидкосного столба (мм рт.ст., мм вод.ст.). Соотношения между единицами давления представлены в приложении 2.
Гидростатическое давление– давление в неподвижной жидкости. Гидростатическое давление обладает следующими свойствами.
10. В любой точке жидкости оно направлено перпендикулярно поверхности внутрь рассматриваемого объема жидкости.
20. Оно неизменно во всех направлениях.
30. Гидростатическое давление в точке зависит от ее координат в пространстве.
Уравнение, позволяющее находить гидростатическое давление в любой точке покоящейся жидкости при условии действия на нее только силы тяжести, называется основным уравнением гидростатики.
p =p0 + ρgh, (2.1)
где р0 – давление на свободной поверхности жидкости, которое передается всем точкам этой жидкости и по всем направлениям без изменения (закон Паскаля); ρ – плотность жидкости; g = 9,8 м/с2 – ускорение свободного падения;h– глубина расположения рассматриваемой точки.
Из основного уравнения гидростатики следует, что полная
сила давления жидкости на плоскую стенку равна произведению площади стенки S на гидростатическое давление рс в центре тяжести этой площади
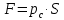
Центр давления – точка приложения силы давления от веса жидкости – располагается ниже центра тяжести или совпадает с последним в случае горизонтальной стенки.
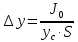
где J0 - момент инерции площади S, проходящей относительно центральной оси, перпендикулярной плоскости стенки;
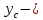координата центра тяжести.Сила давления жидкости на криволинейную стенку определяется как векторная сумма горизонтальной и вертикальной составляющих полной силы:
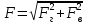
Горизонтальная составляющая численно равна силе давления на площадь вертикальной проекции стенки:
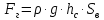
Вертикальная составляющая численно равна весу жидкости в объеме тела давления:
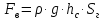
Телом давления называют объем жидкости, ограниченный данной криволинейной поверхностью, вертикальной поверхностью, проведенной через нижнюю образующую криволинейной поверхности, и свободной поверхностью жидкости.
Рекомендации к решению задач
-
При решении задач на определение давления в некоторой точке покоящейся жидкости следует
1) выбрать поверхность равного давления (поверхность уровня) – любая горизонтальная плоскость на произвольной глубине;
2) рассмотреть на этой плоскости любые две точки и записать выражение для определения абсолютного давления в этих точках, используя основное уравнение гидростатики. При этом, необходимо обратить внимание на знак перед вторым членом правой части уравнения: знак «+» ставится в случае увеличения глубины (давление возрастает), «-» – при подъеме (давление уменьшается);
3) записать уравнение равенства давлений в точках, приравняв правые части записанных выражений;
4) из полученного уравнения выразить неизвестную величину.
-
При решении задач, в которых даны поршни или система поршней, следует
1) составить уравнение сил, приложенных к некоторому подвижному телу (поршню);
2) записать формулы для нахождения каждой из сил, действующих на тело. При этом, давление со стороны жидкости нужно определить, используя основное уравнение гидростатики;
3) подставить полученные зависимости в уравнение равновесия сил и выразить неизвестную величину.
Примеры решения задач
Пример 2.1. Определить абсолютное давление p0 на поверхности бензина в закрытом резервуаре, если показания ртутного пьезометра h1, а глубина h2. Значения плотности бензина ρб и ртути ρрт взять в табл.4.1 (приложение 4).
Решение:
Выбираем поверхность равного давления на уровне 1-1. Рассмотрим гидростатическое давление на этом уровне со стороны ртутного пьезометра и резервуара.
Давление в любой точке уровня 1-1 со стороны ртутного пьезометра согласно основному уравнению гидростатики
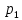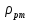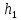
= pа + g Давление со стороны резервуара
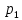= p0 + 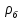g