ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 530
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
рн. Диаметры клапана D, d; жесткость пружины k. Давление справа от большого и слева от малого поршней – атмосферное.
З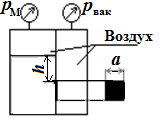
адача 2с.5. Замкнутый резервуар разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной а, закрытое крышкой. Давление над жидкостью Ж в левой части резервуара определяется показаниями манометра рм, давление воздуха в правой части – показаниями мановакуумметра рвак. Определить величину и точку приложения результирующей силы давления на крышку.
Обозначения: Б – бензин, В – вода, Г – глицерин, К – керосин, Мтр – масло трансформаторное, Мтурб – масло турбинное, Н – нефть.
Гидравлические сопротивления
Основными законами, позволяющими решать простейшие задачи о движении жидкостей, являются уравнение Бернулли и уравнение расхода.
Уравнение расхода
– условие неразрывности потока несжимаемой жидкости – записывается в виде равенства объемных расходов в любых сечениях трубопровода:
Q =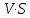
= сonst
Отсюда следует, что средние скорости неразрывного потока обратно пропорциональны площадям этих сечений.
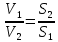
В некоторых задачах о движении жидкости в приближении рассматривается идеальная (невязкая) жидкость.
Уравнение Бернулли для потока идеальной жидкости представляет закон сохранения энергии жидкости вдоль потока: вдоль элементарной струйки идеальной жидкости сумма потенциальной и кинетической энергии является постоянной величиной, т.е.
,
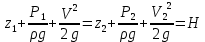где Н - полный гидродинамический напор (полная удельная энергия жидкости в сечении); Z – вертикальная координата центров тяжести сечений (геометрический напор);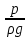
– пьезометрический напор (удельная энергия давления); U/2g – скоростной напор (удельная кинетическая энергия), сумма 
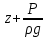представляет собой потенциальную энергию.
В реальных жидкостях проявляется влияние сил внутреннего трения, обусловленных вязкостью, на преодоление которых расходуется определенное количество кинетической энергии или скоростного напора h.
Уравнение Бернулли для потока реальной жидкости записывается в следующем виде
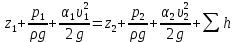
где υ - средняя по сечению скорость; α – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечениям (α=1 только при равномерном распределении скоростей (турбулентный режим движения жидкости)).
Член h выражает потери напора на преодоление различных сопротивлений на пути движения жидкости:
Потери напора, вызванные этим видом сопротивлений, называют
линейными -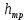
.
Потери напора, вызванные этим видом сопротивлений, называют местными -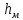
.
Линейные потери напора определяют с помощью формулы Дарси:
,
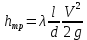где l– длина рассматриваемого участка трубопровода; d – диаметр трубопровода; λ – безразмерный коэффициент гидравлического трения.
λ зависит от режима движения жидкости, и определяется числом Рейнольдса, который для трубопровода с круглым сечением вычисляется по формуле:
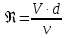
Для потока произвольной формы число Рейнольдса выражается через гидравлический радиус
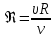
Смена режимов происходит при критическом значении числа Рейнольдса, которое составляет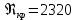
. Если число Рейнольдса больше критического значения, то режим движения турбулентный, если меньше – то ламинарный. Критическое значение числа Рейнольдса соответствует нижней критической скорости.
При ламинарном режиме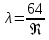
;
при турбулентном λ зависит от числа Рейнольдса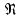
и относительной шероховатости трубы ε
: 
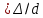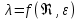
Местные потери напораопределяются по формуле Вейсбаха:
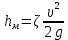
где υ – средняя скорость потока в сечении перед местным сопротивлением ζ – коэффициент местного сопротивления (определяется формой местного сопротивления и его геометрическими параметрами).
При внезапном расширении трубы потеря напора происходит при вводе жидкости в силовые цилиндры, пневмогидравлические аккумуляторы, фильтры и прочие устройства. Величина этой потери равна скоростному напору потерянной скорости (теорема Борда):
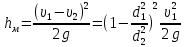
Обозначим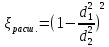
- коэффициент местных сопротивлений при расширении трубы, где d1 и d2 – внутренние диаметры сечений трубы перед и за расширением.
В случае внезапного сужения трубопровода коэффициент местных сопротивлений равен
,
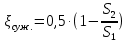где S1 и S2 – площади сечений трубы до и после сужения.
Рекомендации к решению задач
Для решения задачи с применением уравнения Бернулли следует
1. выбрать два сечения, для которых записывается уравнение. В качестве сечений рекомендуется брать:
- выход в атмосферу, где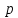
абс = ра;
- свободную поверхность в резервуаре, где скорость V = 0
- сечение, в котором присоединен прибор для измерения давления (манометр, вакуумметр, пьезометр).
2. записать уравнение Бернулли в общем виде;
3. переписать уравнение для заданных сечений с заменой его членов заданными буквенными величинами и исключить члены, равные нулю.
При этом необходимо помнить:
- уравнение Бернулли записывается по течению жидкости;
- вертикальная ордината z всегда отсчитывается от произвольной горизонтальной плоскости вверх;
- давление р, входящее в правую и левую части уравнения, должно быть задано в одной системе отсчета (абсолютной или избыточной);
- коэффициент Кориолиса в задачах на движение потока реальной жидкости следует учитывать только при ламинарном режиме течения α = 2, для турбулентных потоков можно принимать α = 1;
- суммарная потеря напора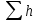
записывается в правой части уравнения со знаком «+» и складывается из местных потерь, которые определяются формулой Вейсбаха, и потерь на трение по длине, определяемых формулой Дарси.
Примеры решения задач
П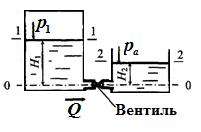
ример 3.1. Горизонтальная труба диаметром d = 5 см соединяет резервуары с водой, в которых поддерживаются постоянные уровни
| Величина | Варианты | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| рн, МПа | 0,8 | 1,5 | 3 | 1 | 1,2 | 1,8 | 2 | 2,2 | 2,4 | 2,6 |
| D, мм | 24 | 22 | 22 | 24 | 20 | 20 | 18 | 28 | 28 | 24 |
| d, мм | 18 | 18 | 20 | 20 | 18 | 16 | 16 | 22 | 24 | 18 |
| k, Н/мм | 6 | 7 | 8 | 5 | 4 | 6 | 7 | 8 | 4 | 7 |
З
адача 2с.5. Замкнутый резервуар разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной а, закрытое крышкой. Давление над жидкостью Ж в левой части резервуара определяется показаниями манометра рм, давление воздуха в правой части – показаниями мановакуумметра рвак. Определить величину и точку приложения результирующей силы давления на крышку.| Величина | Вариант | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Ж | В | Б | К | В | Мтр | Г | Н | К | Мтурб | Б |
| рм, ат | 0,8 | 0,9 | 0,7 | 0,8 | 0,5 | 0,9 | 1,0 | 0,3 | 1,0 | 0,5 |
| рвак, ат | 0,1 | 0,1 | 0,2 | 0,2 | 0,3 | 0,3 | 0,1 | 0,1 | 0,2 | 0,2 |
| a, мм | 200 | 300 | 400 | 100 | 200 | 300 | 200 | 100 | 400 | 200 |
Обозначения: Б – бензин, В – вода, Г – глицерин, К – керосин, Мтр – масло трансформаторное, Мтурб – масло турбинное, Н – нефть.
-
Основные законы движения жидкости.
Гидравлические сопротивления
Основными законами, позволяющими решать простейшие задачи о движении жидкостей, являются уравнение Бернулли и уравнение расхода.
Уравнение расхода
– условие неразрывности потока несжимаемой жидкости – записывается в виде равенства объемных расходов в любых сечениях трубопровода:
Q =
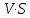= сonstОтсюда следует, что средние скорости неразрывного потока обратно пропорциональны площадям этих сечений.
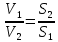
В некоторых задачах о движении жидкости в приближении рассматривается идеальная (невязкая) жидкость.
Уравнение Бернулли для потока идеальной жидкости представляет закон сохранения энергии жидкости вдоль потока: вдоль элементарной струйки идеальной жидкости сумма потенциальной и кинетической энергии является постоянной величиной, т.е.
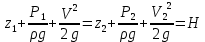,где Н - полный гидродинамический напор (полная удельная энергия жидкости в сечении); Z – вертикальная координата центров тяжести сечений (геометрический напор);
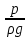– пьезометрический напор (удельная энергия давления); U/2g – скоростной напор (удельная кинетическая энергия), сумма 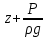представляет собой потенциальную энергию.В реальных жидкостях проявляется влияние сил внутреннего трения, обусловленных вязкостью, на преодоление которых расходуется определенное количество кинетической энергии или скоростного напора h.
Уравнение Бернулли для потока реальной жидкости записывается в следующем виде
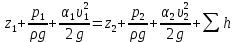
где υ - средняя по сечению скорость; α – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечениям (α=1 только при равномерном распределении скоростей (турбулентный режим движения жидкости)).
Член h выражает потери напора на преодоление различных сопротивлений на пути движения жидкости:
-
Сопротивления по всей длине потока жидкости, вызванные силами трения частиц жидкости между соседними слоями жидкости и трением о стенки, ограничивающие поток.
Потери напора, вызванные этим видом сопротивлений, называют
линейными -
.-
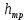Сопротивления, обусловленные местными препятствиями, встречающимися на пути движения (изменение формы и размеров русла). Они ведут к изменению величины и направления скорости.
Потери напора, вызванные этим видом сопротивлений, называют местными -
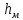.Линейные потери напора определяют с помощью формулы Дарси:
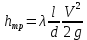,где l– длина рассматриваемого участка трубопровода; d – диаметр трубопровода; λ – безразмерный коэффициент гидравлического трения.
λ зависит от режима движения жидкости, и определяется числом Рейнольдса, который для трубопровода с круглым сечением вычисляется по формуле:
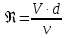
Для потока произвольной формы число Рейнольдса выражается через гидравлический радиус
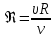
Смена режимов происходит при критическом значении числа Рейнольдса, которое составляет
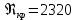. Если число Рейнольдса больше критического значения, то режим движения турбулентный, если меньше – то ламинарный. Критическое значение числа Рейнольдса соответствует нижней критической скорости.При ламинарном режиме
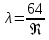;при турбулентном λ зависит от числа Рейнольдса
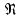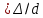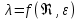
и относительной шероховатости трубы ε : Местные потери напораопределяются по формуле Вейсбаха:
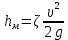
где υ – средняя скорость потока в сечении перед местным сопротивлением ζ – коэффициент местного сопротивления (определяется формой местного сопротивления и его геометрическими параметрами).
При внезапном расширении трубы потеря напора происходит при вводе жидкости в силовые цилиндры, пневмогидравлические аккумуляторы, фильтры и прочие устройства. Величина этой потери равна скоростному напору потерянной скорости (теорема Борда):
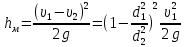
Обозначим
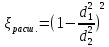- коэффициент местных сопротивлений при расширении трубы, где d1 и d2 – внутренние диаметры сечений трубы перед и за расширением.В случае внезапного сужения трубопровода коэффициент местных сопротивлений равен
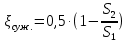,где S1 и S2 – площади сечений трубы до и после сужения.
Рекомендации к решению задач
Для решения задачи с применением уравнения Бернулли следует
1. выбрать два сечения, для которых записывается уравнение. В качестве сечений рекомендуется брать:
- выход в атмосферу, где
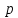абс = ра;- свободную поверхность в резервуаре, где скорость V = 0
- сечение, в котором присоединен прибор для измерения давления (манометр, вакуумметр, пьезометр).
2. записать уравнение Бернулли в общем виде;
3. переписать уравнение для заданных сечений с заменой его членов заданными буквенными величинами и исключить члены, равные нулю.
При этом необходимо помнить:
- уравнение Бернулли записывается по течению жидкости;
- вертикальная ордината z всегда отсчитывается от произвольной горизонтальной плоскости вверх;
- давление р, входящее в правую и левую части уравнения, должно быть задано в одной системе отсчета (абсолютной или избыточной);
- коэффициент Кориолиса в задачах на движение потока реальной жидкости следует учитывать только при ламинарном режиме течения α = 2, для турбулентных потоков можно принимать α = 1;
- суммарная потеря напора
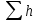записывается в правой части уравнения со знаком «+» и складывается из местных потерь, которые определяются формулой Вейсбаха, и потерь на трение по длине, определяемых формулой Дарси.Примеры решения задач
П
ример 3.1. Горизонтальная труба диаметром d = 5 см соединяет резервуары с водой, в которых поддерживаются постоянные уровни