5. Гидравлический расчет трубопроводов

Все трубопроводы подразделяются на две категории: простые и сложные. Простой трубопровод не имеет разветвлений на пути движения жидкости, но может представлять последовательное соединение труб разного диаметра. Сложный трубопровод имеет хотя бы одно разветвление и может содержать как параллельные и последовательные соединения труб.

При изучении устройства автомобилей приходится сталкиваться с масло- и бензопроводами небольшой длины, движение жидкости в которых обусловлено работой насосов.

Если в трубопроводе необходимо обеспечить расход жидкости Q, то потребный для этого напор Н_потр. – пьезометрическая высота в начальном сечении определяется по формуле

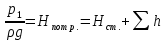, (5.1)

где 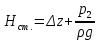– статический напор, - суммарные потери напора на сопротивление в трубопроводе.

Суммарная потеря напора складывается из потерь на трение по всей длине трубы и местных потерь

= +

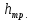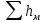
Для определения потерь напора на трение по длине удобно воспользоваться формулой Дарси, которую для дальнейших расчетов удобно выразить через расход:

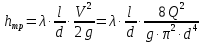(5.2)

При турбулентном коэффициент сопротивления трениязависит от числа Рейнольдса и относительной шероховатости трубы ε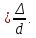 Значения эквивалентной шероховатости Δ для различных труб представлены в Приложении 6.

Универсальной формулой, учитывающей одновременно оба фактора является формула Альтшуля:

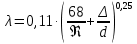(5.3)

Для гидравлически гладких труб шероховатость на сопротивление не влияет, и коэффициент сопротивления

---

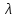
однозначно определяется числом Рейнольдса:

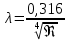(5.4)

C учетом формул Альтшуля и Вейсбаха,

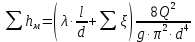= + (5.5)

Данная формула справедлива для обоих режимов, однако для ламинарного режима удобнее использовать формулу Пуазейля:

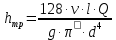, (5.6)

в которой необходимо заменить фактическую длину трубопровода расчетной, равной

,

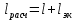где 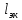– длина, эквивалентная всем местным гидравлическим сопротивлениям в трубопроводе.

Формула для расчета потребного напора имеет вид

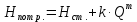, (5.7)

где для ламинарного режима течения

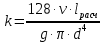, m=1; (5.8)

турбулентного режима течения

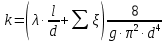, m=2 (5.9)

Характеристики потребного напора 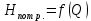и суммарных потерь напора трубопроводов = 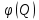при ламинарном режиме представляет прямые, при турбулентном - параболы.

Для трубопровода, состоящего из n последовательно соединенных участков, справедливы следующие равенства

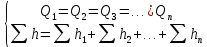(5.10)

Для параллельного соединения n трубопроводов (n – количество разветвлений) характерна следующая система уравнений

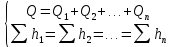(5.11)
Рекомендации к решению задач
Задачи на расчет простого трубопровода делятся на три типа.

1 тип. Даны: расход жидкости Q в трубопроводе, его геометрические параметры (l

---

,d,Δz), шероховатость труб; давление в конечном сечении (либо в начальном для всасывающих трубопроводов) и свойства жидкости (ρ,ν). Местные сопротивления заданы коэффициентами ζ либо оцениваются по справочным данным.

Требуется найти потребный напор H_потр.

Алгоритм решения:

1. 
   Определить режим течения. С этой целью нужно найти число Рейнольдса Re по известным Q, d и ν.
   
2. 
   При ламинарном режиме напор вычисляется по формулам (5.7) и (5.8)
   
3. 
   При турбулентном режиме задача решается с помощью формул (5.3) или (5.4) в зависимости от шероховатости труб.
   

2 тип. Даны: располагаемый напор H_расп, все величины, перечисленные в задаче 1-го типа, кроме расхода Q.

Так как число Рейнольдса Re нельзя вычислить, то режимом движения необходимо задаться, основываясь на роде жидкости. Для вязких жидкостей (масло) выбирать ламинарный режим течения, для маловязких (вода, бензин, керосин) – турбулентный. Для проверки правильности выбора в конце решения необходимо вычислить число Рейнольдса. Либо по формулам (5.7) и (5.8) выразить диаметр через критическое число Рейнольдса и определить H_кр, соответствующее смене режима. Сравнивая H_кр и H_расп, определяют режим течения.

При ламинарном режиме задача решается на основании формул (5.7) и (5.8).

При турбулентном режиме в уравнениях (5.7) и (5.9) содержаться две неизвестныеQи λ_т, зависящие от числа Рейнольдса. В этом случае для решения задачи требуется метод последовательных приближений. Для этого в первом приближении следует задаться коэффициентом λ_т. Выбрав начальное значение λ_т, решить задачу по 1-му типу. По полученным данным следует заново найти λ_т и повторить все вычисления, приближаясь к истинному результату.

3 тип. Даны: располагаемый напор H_расп, расход жидкости Qв трубопроводе, его геометрические параметры и свойства жидкости, перечисленные выше, кроме диаметра трубопровода d.

Так как число Рейнольдса Re нельзя вычислить, то режимом движения либо необходимо задаться, либо по формулам (5.7) и (5.8) выразить диаметр через критическое число Рейнольдса и определить H_кр, соответствующее смене режима. Сравнивая H_кр и H_расп, определяют режим течения.

При ламинарном режиме задача решается на основании формул (5.7) и (5.8).

При турбулентном режиме решение нужно проводить с использованием графиков. Для этого следует

---

1) задать ряд значений диаметра d и по ним подсчитать H_потр;

2) построить график H_потр = f(d);

3) по графику, зная H_расп, определить d.
Среди задач на расчет сложных трубопроводов наиболее частыми являются задачи на параллельные трубопроводы, которые решаются с помощью системы уравнений (5.11)

Алгоритм решения:

1. 
   Определить режим движения, вычислив число Рейнольдса;
   
2. 
   с учетом режима течения выразить суммарные потери напора через параметры, определяющие сопротивления трубопроводов;
   
3. 
   составить систему уравнений, число которых равно числу параллельных участков;
   
4. 
   решить систему уравнений.
   

Для разветвленных трубопроводов число неизвестных в системе уравнений на единицу больше числа ветвей потому, что добавляется потребный напор в точке разветвления.
Примеры решения задач
П 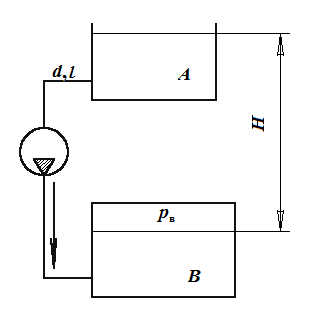ример 5.1. Вода, перекачивается насосом из открытого бака А в расположенный ниже резервуар B, где поддерживается постоянное давление р_в = 0,18 МПа (абс.) по трубопроводу общей длиной 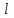= 225 м и диаметром 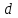=250 мм. Разность уровней воды в баках h=3 м. Определить потребный напор, создаваемый насосом для подачи в бак B расхода воды 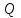= 98 л/с. Принять суммарный коэффициент местных сопротивлений ζ = 6,5. Эквивалентная шероховатость стенок трубопровода Δ = 0,15 мм. Жидкость – вода с плотностью ρ = 1000 кг/м³ и вязкостью ν = 0,01 Ст. Атмосферное давление р_а = 0,1 МПа.
Решение: Потребный напор, создаваемый насосом для подачи в бак B расхода воды 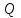равен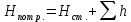



Статический напор складывается из пьезометрической высоты на поверхности жидкости в резервуаре В 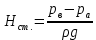и разности уровней воды в резервуарах

---

h. Т.к. вода перекачивается в нижний бак, то вторую составляющую подставляем со знаком «-».

Потери напора складываются из потерь напора на трение по длине трубопровода и потерь на местных сопротивлениях .

Таким образом



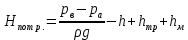
Потери напора по длине трубопровода определим по формуле Дарси, записав ее через расход: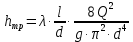



Для правильного вычисления коэффициента трения λ определим режим течения жидкости в трубопроводе:



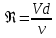
Согласно уравнению неразрывности скорость движения жидкости в трубопроводе



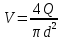
Тогда формула числа Рейнольдса примет вид:



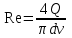
Подставив значения, определим режим течения жидкости:

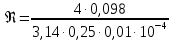= 49911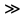0 2320

Величина числа Рейнольдса указывает на турбулентный режим движения. Для такого значения числа 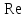коэффициент трения вычислим по универсальной формуле Альтшуля:



Вычислим коэффициент Дарси:



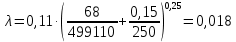
Вычислим потери напора по длине трубопровода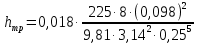

=3,291 м.
Местные потери напора определим по формуле Вейсбаха, записав ее через расход: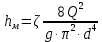

Вычислим местные потери :

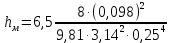= 1,32 м.

Окончательно подставив полученные значения, определим потребный напор, используя для расчета избыточное давление в баке

---

Смотрите также файлы

• 29 Керім Тленшин атындаы жалпы орта мектебіні Оуа штар мектеп.docx

• 1 Пока нет ответа Балл 1,00 Отметить вопрос Текст вопроса , darf mich niemand stren. Выберите один ответ a. Bevor ich lernte b. Als ich lerne c. Whrend ich lerne d. Bevor ich lerne Очистить мой выбор Вопрос 2.docx

• Уровень 2 V1 Психология ылымы нені зерттейді.docx

• Определение эффективного алгоритма сортировки на основе эмпирического и асимптотического.docx

• Рабочая программа учебной дисциплины Основы безопасности жизнедеятельности.pdf