;; = 5,1 / (9,81 0,52310^-3) кг/м³.

Пример 4. Трубопровод диаметром d = 500 мм и длинойL = 1000 м наполнен водой при давлении 400 кПа, и температуре воды 5⁰C. Определить, пренебрегая деформациями и расширением стенок труб, давление в трубопроводе при нагревании воды в нем до 15 ⁰C, если коэффициент объемного сжатия _w = 5,18 10^-10 Па^-1, а коэффициент температурного расширения _t = 150 10^-60С^-1.

Решение. Находим объем воды в трубе при t = 5 ⁰C

; W = 0,785 0,5²  1000 = 196,25 м³; находим увеличение объема W при изменении температуры

; ;

W = 196,25 10 150 10^-6 = 0,29м³;находим приращение давления в связи с увеличением объема воды

;p = 0,29 / (196,25 5,18 10^-10) = 2850 кПа; давление в трубопроводе после увеличения температуры

400 кПа + 2850 кПа = 3250 кПа = 3,25 МПа.

 

Пример 5. Вязкость нефти, определенная по вискозиметру Энглера, составляет 8,5 ⁰Е. Определить динамическую вязкость нефти, если ее плотность  = 850 кг/м³.

Решение. Находим кинематическую вязкость по формуле Убеллоде

;

 = (0,0731 8,5 – 0,0631/8,5) 10^-4=6,14 10^-5 м²/с;

находим динамическую вязкость нефти

;  = 0,614 10^-4 850 = 0,052 Па с.

 

Пример 6. Определить коэффициент динамической и кинематической вязкости воды, если шарик d = 2 мм из эбонита с  = 1,2 10³ кг/м³ падает в воде с постоянной скоростью u = 0,33 м/с. Плотность воды =10³ кг/м³.

Решение. При движении шарика в жидкости с постоянной скоростью сила сопротивления равняется весу шарика. Сила сопротивления определяется по формуле Стокса:

.

Вес шарика определяется по формуле

.

Так как G=F ,то

.

Следовательно, коэффициент динамической вязкости определится

;  = 1,2 10³  9,81 (2 10^-3)² / (18 0,33) = 0,008 Па с.

Коэффициент кинематической вязкости

;

 = 0.008 / 10³ = 8 10^-6 м²/с.

 

Пример 7. При гидравлическом испытании системы объединенного внутреннего противопожарного водоснабжения допускается падение давления в течение 10 мин

---

. на p = 4,97104 Па. Определить допустимую утечку W при испытании системы вместимостью W = 80 м³.
Коэффициент объемного сжатия _w= 5 10^-10Па^-1.

Решение. Допустимую утечку W определяем из формулы

;                              ;

W = 5 10^-10 80  4,9 10⁴ = 1,96 10^-3 м³.

2. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ

2.1. Сведения из теории

На жидкость, находящуюся в состоянии покоя, действуют силы, которые можно разделить на поверхностные и массовые.

Поверхностные силы приложены к частицам жидкости, находящимся на поверхности раздела данной жидкости и другой среды (реакция стенки сосуда, сила давления поршня, сила давления газа на свободную поверхность).

Массовые силы воздействуют на все частицы данного объема жидкости и пропорциональны массе каждой частицы (силы тяжести, силы инерции, центробежные силы).

Основным понятием гидростатики является понятие гидростатического давления.

Выделим, в находящейся в равновесии жидкости, некоторый объем произвольной формы. Рассечем его на две части I и II плоскостью AB (рис. 2.1).

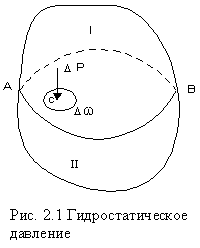Воздействие части I жидкости на часть II будет передаваться по плоскости раздела AB. Выделим на плоскости раздела площадку площадью . Заменим воздействие части I на эту площадку силой . Сила воздействия , приходящаяся на эту площадку называется силой гидростатического давления.

Отношение силы к площади

                                                                                                                     (2.1)

представляет среднее гидростатическое давление.

Если площадь стремится к 0, то отношение будет стремиться к пределу, который называется гидростатическим давлением в точке

 

                                                                                                                    (2.2)

Гидростатическое давление направлено всегда по внутренней нормали к площадке, на которой это давление действует и является сжимающим напряжением, потому что в покоящейся жидкости не могут существовать касательные и растягивающие усилия. Величина гидростатического давления в любой точке жидкости по всем направлениям одинакова.

Гидростатическое давление зависит от положения рассматриваемой точки внутри жидкости и от внешнего давления, действующего на свободной поверхности жидкости. Гидростатическое давление имеет размерность напряжения, т.е.

---

. Измеряют давление в Н/м² (Паскаль). Атмосферное давление измеряют технической атмосферой равной 98100 Па или физической равной 101325 Па, иногда используется единица бар (1бар=10⁵Па).

Различают давление абсолютное (иногда употребляют термин ‘’полное‘’) и избыточное. Абсолютным называется давление, определённое с учетом атмосферного давления. Избыточное давление это давление сверх атмосферного, определенное без учета атмосферного.

;                                                           (2.3)

Абсолютное давление не может быть отрицательным, так как жидкость не воспринимает растягивающих напряжений . Избыточное давление может быть и больше и меньше нуля . Для удобства, отрицательное избыточное давление, взятое со знаком плюс, называют вакуумметрическим давлением

                                                                                                             (2.4)

Очень часто избыточное давление называют манометрическим, так как оно измеряется с помощью манометров, или пьезометрическим, так как оно измеряется с помощью пьезометров.

2.1.1. Основное уравнение гидростатики

В 1755 г. Л. Эйлером были получены дифференциальные уравнения равновесия жидкости:

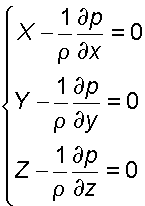                                                                                                 (2.5)

где – градиенты давления в направлении соответствующих координатных осей; X, Y, Z – проекции единичных массовых сил на соответствующие координатные оси; - плотность жидкости.

После незначительных преобразований данную систему уравнений можно представить в виде уравнения

.                                                                              (2.6)

Полученное уравнение выражает изменение давления вдоль координатных осей в общем случае равновесия, и называется основным дифференциальным уравнением гидростатики.

Поверхностью уровня называется такая поверхность, во всех точках которой рассматриваемая функция имеет одно и то же значение. Для задач гидравлики особое значение имеет поверхность равного давления. Эту поверхность будем называть поверхностью уровня.

Так как во всех точках поверхности уровня гидростатическое давление одинаково

---

, то есть ,то . Из основного дифференциального уравнения гидростатики имеем:

                                                                                 (2.7)

поскольку плотность не равна нулю ,запишем

                                                                                     (2.8)

поверхность уровня имеет следующие свойства:

1) две поверхности уровня не пересекаются между собой;

2) массовые силы направлены нормально к поверхности уровня.

Поверхность уровня на границе жидкой и газообразной среды называется свободной поверхностью.

 

2.1.2. Давление при абсолютном покое

Рассмотрим случаи равновесия жидкости, находящейся в сосуде, в состоянии абсолютного покоя под действием сил тяжести и внешнего давления на свободной поверхности. В этом случае проекции единичной силы тяжести на координатные оси равны: .

После подстановки в уравнение (2.6) получаем

.                                                                                                               (2.9)

После интегрирования имеем

.                                                                                                      (2.10)

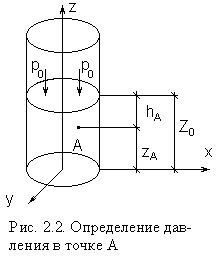Постоянную интегрирования С находим из граничных условий
(рис. 2.2): при ;

.                                                                                          (2.11)

После совместного решения уравнений (2.6) и (2.7) получаем

.

или

                                                                                                     (2.12)

Полученное уравнение является основным уравнением гидростатики, позволяющие определять любое давление в точке.

2.1.3. Поверхность уровня при абсолютном покое

Дифференциальное уравнение поверхности уровня в этом случае имеет вид:

или                                                                                              (2.13)

интегрируя, находим

.                                                                                                              (2.14)

Так как - произвольная постоянная, то это уравнение будет уравнением семейства горизонтальных плоскостей. Таким образом, поверхность уровня есть горизонтальная плоскость, следовательно, и свободная поверхность будет горизонтальной плоскостью.

---

2.1.4. Анализ основного уравнения гидростатики

Как уже отмечалось, основное уравнение гидростатики служит для определения величины гидростатического давления в любой точке покоящейся жидкости

.                                                                                                          (2.15)

Анализируя основное уравнение гидростатики можно сделать следующие выводы:

1. 
   Гидростатическое давление есть сумма внешнего давления, действующего на свободной поверхности и весового давления, создаваемого весом столба жидкости высотой ;
   
2. 
   Внешнее давление не зависит от координат рассматриваемых точек, то есть оно передается во все точки покоящейся жидкости без изменения, поэтому жидкость используется как среда для передачи давления. На этом свойстве жидкости основано действие гидравлических машин (гидропрессы, силовые цилиндры, гидродомкраты);
   
3. 
   Весовое давление является функцией координат точки. С увеличением заглубления точки под свободную поверхность, давление возрастает;
   
4. 
   Внешнее давление может быть больше атмосферного, меньше атмосферного и равно атмосферному. Если численное значение определено с учетом атмосферного, то давление по формуле (2.15) будет абсолютным; если определено без учета атмосферного, то
   

будет избыточным.

2.1.5. Пьезометрическая и вакуумметрическая высоты

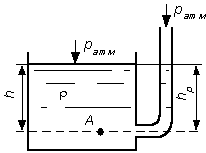    Рис 2.3. Условие равновесия для открытого сосуда

Рассмотрим условия равновесия для открытого сосуда, заполненного жидкостью, к которому в точке А присоединена открытая сверху трубка (рис. 2.3). Под действием весового или избыточного давления , жидкость поднимается в трубке на высоту . Указанная трубка называется пьезометром, а высота – пьезометрической высотой.

Представим основное уравнение гидростатики относительно плоскости, проходящей через точку А. Давление в точке А со стороны сосуда определяется как:

                                                                                                 (2.16)

со стороны пьезометра:

                                                                                                 (2.17)

тогда:

---

Смотрите также файлы

• Диаграммы вокруг нас.docx

• Что такое атом.pptx

• Монография Белгород 2023 удк 338. 212 Ббк 63. 3(2)я7367. 3(2)я73 М74 Рецензенты.doc

• Тема Физиология нервной клетки.docx

• Список литературы 5.docx