Файл: Определение надежности технологической операции механической обработки детали упмбп. 19. 18.docx
Добавлен: 22.11.2023
Просмотров: 107
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2.6 Построение кривой нормального распределения
Кривую нормального распределения размеров детали в партии строят с целью выявления вероятного процента брака всей партии, обработанных заготовок. Для построения кривой сначала необходимо найти: смещение оси симметрии поля рассеяния относительно оси ординат, максимум функции ymax, точки перегиба yA и yB, и значение функции, в котором ветви кривой нормального распределения асимптотически приближаются к оси абсцисс точки yC и yD. Чтобы определить их, проведем расчеты по следующим уравнениям.
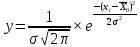(2.22)
Где e – основание натурального логарифма.
Кривая нормального распределения симметрична относительно оси симметрии. Значениям xi и xi соответствует одинаковая величина y.
Кривая имеет максимум, определяемый по формуле 2.23:
На расстоянии ±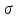
от кривая имеет две точки перегиба (точки А и В). Ордината точек перегиба определяется по формуле 2.24:
Начиная с расстояния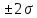
от , ветви кривой нормального распределения асимптотически приближаются к оси абсцисс (точки C и D). Ордината точек определяется по формуле 2.25:
Начиная с расстояния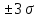
от , ветви кривой нормального распределения асимптотически приближаются к оси абсцисс (точки Е и F). Ордината точек определяется по формуле 2.26:
Данные для построения кривой необходимо занести в таблицу 2.9
Таблица 2.9 – Данные для построения кривой плотности распределения
Продолжение таблицы 2.9
По результатам расчета строится график кривой распределения, изображенный на рисунке 2.2.
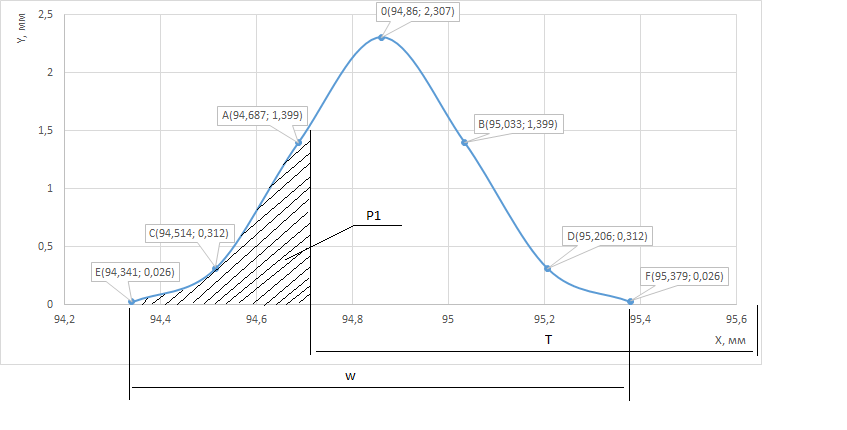
Рисунок 2.2 – График кривой распределения
По графику видно, что поле рассеяния размеров заготовок превосходит поле допуска, поэтому обработка без брака невозможна. Также можно сказать, что для обрабатываемого вала выделенная штриховкой площадь Р1 – это неисправимый брак, исправимого брака в данном случае нет.
2.7 Интервальные оценки параметров распределения
Выборочные характеристики x и 2 S являются надежными количественными оценками генеральных характеристик a и 2 s только при большом объеме выборки. При ограниченных объемах выборки возникает необходимость указать степень точности и надежности оценок генеральных характеристик.
При решении практических задач, связанных со статистическим анализом характеристик изучаемого признака Х, например, механических свойств конструкционных материалов, несущей способности элементов конструкций, пропускной способности нефтегазопроводов, себестоимости единицы производимой продукции и т. д., как правило, значения генеральной дисперсии и математического ожидания неизвестны.
Для оценки генеральной средней M (X ) = a и генерального среднеквадратического отклонения σ по выборочной средней x и выборочному среднеквадратическому отклонению S находят [6] доверительные интервалы по формулам 2.27:
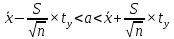(2.27)
Где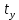
находят из таблицы по заданным n и y (y- уровень доверия или надежность, которая задается заранее).
Для генерального среднего квадратического отклонения доверительные интервалы находят по формулам 2.28 и 2.29:
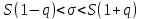(при q<1) (2.28)
или
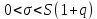(при q>1). (2.29)
Величину q находят по таблице значений q=(y,n) по заданным n и y.
Приведены расчёты:
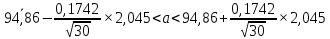
94,79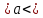
94,92
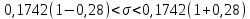
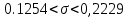
Среднее значение параметров деталей находятся в промежутке от 94,79 мм до 94,92 мм. Отклонение истинных значений случайной величины не должны выходить за пределы 0,1254<????<0,2229.
2.8 Определение процента брака
В тех случаях, когда поле рассеяния размеров заготовок на данной операции превосходит поле допуска (ω > Т), условие обработки без брака не выполняется, и брак является возможным.
При рассеянии размеров по закону Гаусса вероятный процент брака вычисляют, как площадь заштрихованных участков кривой.
Для рассмотрения метода определения вероятных показателей брака в разделе 2.6 была изображена кривая нормального распределения с наложенным полем допуска T, как показано на рисунке, отсюда видно, что все детали выборки (по размеру X), находящиеся в поле допуска, являются годными, а детали, попадающие в поле Р1, являются бракованными.
Для расчета количества вероятного брака необходимо найти удвоенное
значение интеграла, определяющего половину площади, ограниченной кривой Гаусса и абсциссой XA и XB по формуле (2.30):
Формулу можно записать в нормированном виде в форме известной функции Лапласа. Значения этой функции табулированы в зависимости от величины t и приведены в таблицах.
В формуле величина t представляет собой нормированный параметр распределения или коэффициент риска и определяется выражением по формуле 2.32:
где t – преобразованная координата х, определенная из соотношения,
Amin(max) – предельные значения поля допуска.
Необходимо вычислить параметр t по формуле 2.33:
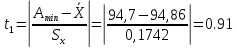
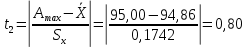
По найденным значениям t1 и t2, вычисленным выше, с помощью таблиц учебной литературы путем интерполяции определяем значения функций Ф(t1) и Ф(t2).
А процент возможного брака определяем из соотношений 2.34 и 2.35
:
где Pиспр, Рнеиспр – процент возможного брака исправимого и неисправимого, %.
Процент годных деталей Pгод определяем по следующей формуле 2.36:
Процент брака мал, поэтому процент годных деталей равен 99,67%.
ЗАКЛЮЧЕНИЕ
В теоретической части работы было выяснено, что теория статистических критериев является частью математической статистики и основывается на теории вероятностей.
Статистические критерии подразделяют на несколько категорий:
1) критерии значимости;
2) критерии согласия;
3) критерии проверки на однородность.
Статистическая проверка гипотез проводится с помощью некоторого статистического критерия по общей логической схеме, включающей нахождение конкретного вида функции от результатов наблюдения (критической статистики), на основании которой принимается окончательное решение. Например, могут рассматриваться гипотезы об общем законе распределения исследуемой случайной величины, об однородности двух или нескольких обрабатываемых выборок, о числовых значениях параметров исследуемой генеральной совокупности и др. Результат проверки может быть либо отрицательным (данные наблюдения противоречат высказанной гипотезе), либо неотрицательным. В первом случае гипотеза ошибочна, во втором – ее нельзя считать доказанной: просто она не противоречит имеющимся выборочным данным, однако таким же свойством могут наряду с ней обладать и другие гипотезы. Для статистической проверки гипотез используются разные критерии. В частности, когда проверяется согласие между выборочным и гипотетическим распределениями, используется критерий согласия, например, критерий Пирсона «хи – квадрат», критерий Колмогорова – Смирнова и др.
Практическая часть позволяет сделать выводы об основных математических характеристиках случайной величины, о точности операции, о грубых погрешностях в выборке, а также о законе распределения выборки.
Таким образом, среднее значение исследуемого размера равно 94,86 мм, среднее квадратичное отклонение, показывающее разброс действительных размеров вала относительно среднего арифметического значения, составляет 0,1729 мм.
Коэффициент точности показывает, что рассматриваемый процесс является точным, так как значение коэффициента меньше 0, 75. Процент брака будет минимальным, о чем говорит значение коэффициента настроенности, близкое к нулю (
). Коэффициент настроенности равен 0,4.
Согласно проверке на грубые погрешности измерений, по методу Грэббса резко выделяющееся значение (95,68 мм) исключается и производится пересчет уточненных характеристик распределения
Кривую нормального распределения размеров детали в партии строят с целью выявления вероятного процента брака всей партии, обработанных заготовок. Для построения кривой сначала необходимо найти: смещение оси симметрии поля рассеяния относительно оси ординат, максимум функции ymax, точки перегиба yA и yB, и значение функции, в котором ветви кривой нормального распределения асимптотически приближаются к оси абсцисс точки yC и yD. Чтобы определить их, проведем расчеты по следующим уравнениям.
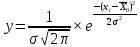(2.22)Где e – основание натурального логарифма.
Кривая нормального распределения симметрична относительно оси симметрии. Значениям xi и xi соответствует одинаковая величина y.
Кривая имеет максимум, определяемый по формуле 2.23: 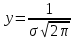 | (2.23) |
На расстоянии ±
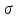от кривая имеет две точки перегиба (точки А и В). Ордината точек перегиба определяется по формуле 2.24:  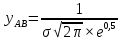| (2.24) |
Начиная с расстояния
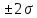от , ветви кривой нормального распределения асимптотически приближаются к оси абсцисс (точки C и D). Ордината точек определяется по формуле 2.25:  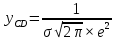| (2.25) |
Начиная с расстояния
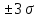от , ветви кривой нормального распределения асимптотически приближаются к оси абсцисс (точки Е и F). Ордината точек определяется по формуле 2.26:  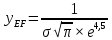| (2.26) |
Данные для построения кривой необходимо занести в таблицу 2.9
Таблица 2.9 – Данные для построения кривой плотности распределения
| Точка xi | x | y |
| A | 94,687 | 1,399 |
Продолжение таблицы 2.9| B | 95,033 | 1,399 |
| C | 94,514 | 0,312 |
| D | 95,206 | 0,312 |
| E | 94,341 | 0,026 |
| F | 95,379 | 0,026 |
| 0 | 94,86 | 2,307 |
По результатам расчета строится график кривой распределения, изображенный на рисунке 2.2.
Рисунок 2.2 – График кривой распределения
По графику видно, что поле рассеяния размеров заготовок превосходит поле допуска, поэтому обработка без брака невозможна. Также можно сказать, что для обрабатываемого вала выделенная штриховкой площадь Р1 – это неисправимый брак, исправимого брака в данном случае нет.
2.7 Интервальные оценки параметров распределения
Выборочные характеристики x и 2 S являются надежными количественными оценками генеральных характеристик a и 2 s только при большом объеме выборки. При ограниченных объемах выборки возникает необходимость указать степень точности и надежности оценок генеральных характеристик. При решении практических задач, связанных со статистическим анализом характеристик изучаемого признака Х, например, механических свойств конструкционных материалов, несущей способности элементов конструкций, пропускной способности нефтегазопроводов, себестоимости единицы производимой продукции и т. д., как правило, значения генеральной дисперсии и математического ожидания неизвестны.
Для оценки генеральной средней M (X ) = a и генерального среднеквадратического отклонения σ по выборочной средней x и выборочному среднеквадратическому отклонению S находят [6] доверительные интервалы по формулам 2.27:
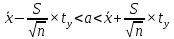(2.27)Где
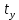находят из таблицы по заданным n и y (y- уровень доверия или надежность, которая задается заранее).Для генерального среднего квадратического отклонения доверительные интервалы находят по формулам 2.28 и 2.29:
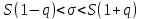(при q<1) (2.28)или
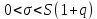(при q>1). (2.29)Величину q находят по таблице значений q=(y,n) по заданным n и y.
Приведены расчёты:
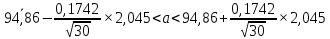
94,79
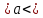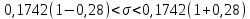
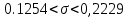
94,92 Среднее значение параметров деталей находятся в промежутке от 94,79 мм до 94,92 мм. Отклонение истинных значений случайной величины не должны выходить за пределы 0,1254<????<0,2229. 2.8 Определение процента брака
В тех случаях, когда поле рассеяния размеров заготовок на данной операции превосходит поле допуска (ω > Т), условие обработки без брака не выполняется, и брак является возможным.
При рассеянии размеров по закону Гаусса вероятный процент брака вычисляют, как площадь заштрихованных участков кривой.
Для рассмотрения метода определения вероятных показателей брака в разделе 2.6 была изображена кривая нормального распределения с наложенным полем допуска T, как показано на рисунке, отсюда видно, что все детали выборки (по размеру X), находящиеся в поле допуска, являются годными, а детали, попадающие в поле Р1, являются бракованными.
Для расчета количества вероятного брака необходимо найти удвоенное
значение интеграла, определяющего половину площади, ограниченной кривой Гаусса и абсциссой XA и XB по формуле (2.30):
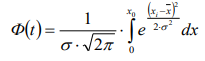 | (2.30) |
Формулу можно записать в нормированном виде в форме известной функции Лапласа. Значения этой функции табулированы в зависимости от величины t и приведены в таблицах.
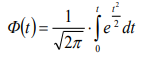 | (2.31) |
В формуле величина t представляет собой нормированный параметр распределения или коэффициент риска и определяется выражением по формуле 2.32: 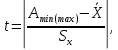 | (2.32) |
где t – преобразованная координата х, определенная из соотношения,
Amin(max) – предельные значения поля допуска.
Необходимо вычислить параметр t по формуле 2.33:
| (2.33) |
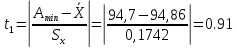
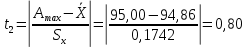
По найденным значениям t1 и t2, вычисленным выше, с помощью таблиц учебной литературы путем интерполяции определяем значения функций Ф(t1) и Ф(t2).
А процент возможного брака определяем из соотношений 2.34 и 2.35
:
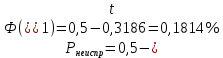 | (2.34) |
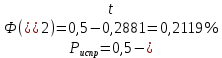 | (2.35) |
| | |
где Pиспр, Рнеиспр – процент возможного брака исправимого и неисправимого, %.
Процент годных деталей Pгод определяем по следующей формуле 2.36:
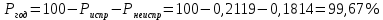 | (2.36) |
Процент брака мал, поэтому процент годных деталей равен 99,67%.
ЗАКЛЮЧЕНИЕ В теоретической части работы было выяснено, что теория статистических критериев является частью математической статистики и основывается на теории вероятностей.
Статистические критерии подразделяют на несколько категорий:
1) критерии значимости;
2) критерии согласия;
3) критерии проверки на однородность.
Статистическая проверка гипотез проводится с помощью некоторого статистического критерия по общей логической схеме, включающей нахождение конкретного вида функции от результатов наблюдения (критической статистики), на основании которой принимается окончательное решение. Например, могут рассматриваться гипотезы об общем законе распределения исследуемой случайной величины, об однородности двух или нескольких обрабатываемых выборок, о числовых значениях параметров исследуемой генеральной совокупности и др. Результат проверки может быть либо отрицательным (данные наблюдения противоречат высказанной гипотезе), либо неотрицательным. В первом случае гипотеза ошибочна, во втором – ее нельзя считать доказанной: просто она не противоречит имеющимся выборочным данным, однако таким же свойством могут наряду с ней обладать и другие гипотезы. Для статистической проверки гипотез используются разные критерии. В частности, когда проверяется согласие между выборочным и гипотетическим распределениями, используется критерий согласия, например, критерий Пирсона «хи – квадрат», критерий Колмогорова – Смирнова и др.
Практическая часть позволяет сделать выводы об основных математических характеристиках случайной величины, о точности операции, о грубых погрешностях в выборке, а также о законе распределения выборки.Таким образом, среднее значение исследуемого размера равно 94,86 мм, среднее квадратичное отклонение, показывающее разброс действительных размеров вала относительно среднего арифметического значения, составляет 0,1729 мм.
Коэффициент точности показывает, что рассматриваемый процесс является точным, так как значение коэффициента меньше 0, 75. Процент брака будет минимальным, о чем говорит значение коэффициента настроенности, близкое к нулю (
). Коэффициент настроенности равен 0,4.Согласно проверке на грубые погрешности измерений, по методу Грэббса резко выделяющееся значение (95,68 мм) исключается и производится пересчет уточненных характеристик распределения