Файл: Определение надежности технологической операции механической обработки детали упмбп. 19. 18.docx
Добавлен: 22.11.2023
Просмотров: 108
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Определяются границы интервалов и заносятся в таблицу 2.6.
Таблица 2.6 – Распределение размеров деталей
| № интервала | Интервалы размеров, мм | Частота n | Частность n/N |
| 1 | 94,695 – 94,865 | 19 | 0.63 |
| 2 | 94,865 – 95,035 | 10 | 0.33 |
| 3 | 95,035 – 95,205 | 0 | 0 |
| 4 | 95,205 – 95,375 | 0 | 0 |
| 5 | 95,375 – 95,545 | 0 | 0 |
| 6 | 95,545 – 95,715 | 1 | 0.033 |
| | | n = 30 | n/N=1 |
По данным таблицы строится гистограмма распределения и полигон практического распределения действительных размеров (рисунок 2.1).
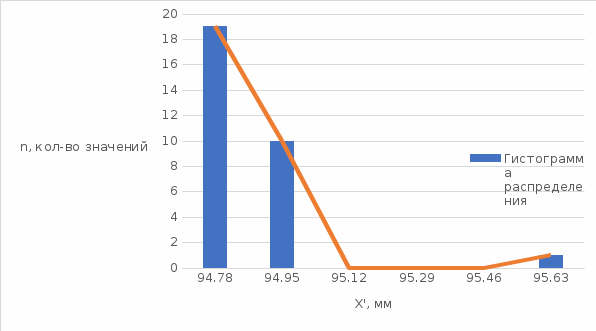
 Рисунок 2.1 – Гистограмма и полигон распределения действительных размеров
Рисунок 2.1 – Гистограмма и полигон распределения действительных размеровИсходя из рисунка 1 можно сделать вывод, что значения находятся в большом разбросе от среднего. Большинство значений попадает в интервал 94,695 – 94,865.
2.5 Проверка статистических гипотез
Для более точной оценки соответствия распределения параметров в выборке распределению параметров в генеральной совокупности предусматривается проверка по критериям согласия (Критерий Пирсона, Романовского, Колмогорова, Шапиро – Уилка).
Статистическая гипотеза – это предположение о распределении вероятностей, которое необходимо проверить по имеющимся данным.
В методических указаниях рассмотрен критерий Шапиро – Уилка. Критерий Шапиро – Уилка применяется для проверки соответствия эмпирического распределения теоретическому нормальному распределению, когда число выборки мало (3 < n < 50).
Расчётное значение критерия получают по формуле (2.18):
 | (2.18) |
| | |
где
 - сумма квадратов отклонений значений выборки от среднего арифметического.
- сумма квадратов отклонений значений выборки от среднего арифметического.Значение В находят по формуле (2.19):
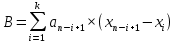 | (2.19) |
где
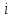 – номер элемента в вариационном ряду
– номер элемента в вариационном рядуai – табличный коэффициент.
 Значение
Значение  находят по формуле (2.20):
находят по формуле (2.20): 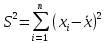 | (2.20) |
Для удобства вычислений составляется таблица 2.7.
Таблица 2.7 – Расчет критерия Шапиро – Уилка
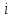 | 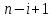 | 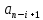 | 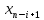 | 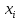 | 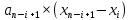 |
| 1 | 30 | 0,4254 | 95 | 94,95 | 0,02127 |
| 2 | 29 | 0,2944 | 94,95 | 94,73 | 0,064768 |
| 3 | 28 | 0,2487 | 94,8 | 95,68 | -0,218856 |
| 4 | 27 | 0,2148 | 94,76 | 94,87 | -0,023628 |
| 5 | 26 | 0,187 | 94,89 | 94,74 | 0,02805 |
| 6 | 25 | 0,163 | 94,91 | 94,81 | 0,0163 |
Продолжение таблицы 2.7
| 7 | 24 | 0,1415 | 94,78 | 94,98 | -0,0283 |
| 8 | 23 | 0,1219 | 94,7 | 94,82 | -0,014628 |
| 9 | 22 | 0,1036 | 94,84 | 94,75 | 0,009324 |
| 10 | 21 | 0,0862 | 94,75 | 94,88 | -0,011206 |
| 11 | 20 | 0,0697 | 94,83 | 94,83 | 0 |
| 12 | 19 | 0,0537 | 94,72 | 94,71 | 0,000537 |
| 13 | 18 | 0,0381 | 94,86 | 94,89 | -0,001143 |
| 14 | 17 | 0,0227 | 94,94 | 94,84 | 0,00227 |
| 15 | 16 | 0,0076 | 94,79 | 94,77 | 0,000152 |
| Сумма: | -0,15509 | ||||
 Для расчета суммы квадратов отклонений значений выборки от среднего арифметического также составляется таблица 2.8.
Для расчета суммы квадратов отклонений значений выборки от среднего арифметического также составляется таблица 2.8. Таблица 2.8 – Расчет суммы квадратов отклонений
| № измерения |  | 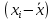 | 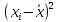 |
| 1 | 94,95 | 0,0910 | 0,0083 |
| 2 | 94,73 | -0,1290 | 0,0166 |
| 3 | 95,68 | 0,8210 | 0,6740 |
| 4 | 94,87 | 0,0110 | 0,0001 |
| 5 | 94,74 | -0,1190 | 0,0142 |
| 6 | 94,81 | -0,0490 | 0,0024 |
| 7 | 94,98 | 0,1210 | 0,0146 |
| 8 | 94,82 | -0,0390 | 0,0015 |
| 9 | 94,75 | -0,1090 | 0,0119 |
| 10 | 94,88 | 0,0210 | 0,0004 |
| 11 | 94,83 | -0,0290 | 0,0008 |
| 12 | 94,71 | -0,1490 | 0,0222 |
| 13 | 94,89 | 0,0310 | 0,0010 |
| 14 | 94,84 | -0,0190 | 0,0004 |
| 15 | 94,77 | -0,0890 | 0,0079 |
| 16 | 94,79 | -0,0690 | 0,0048 |
| 17 | 94,94 | 0,0810 | 0,0066 |
| 18 | 94,86 | 0,0010 | 0,0000 |
 Продолжение таблицы 2.8
Продолжение таблицы 2.8| 19 | 94,72 | -0,1390 | 0,0193 |
| 20 | 94,83 | -0,0290 | 0,0008 |
| 21 | 94,75 | -0,1090 | 0,0119 |
| 22 | 94,84 | -0,0190 | 0,0004 |
| 23 | 94,7 | -0,1590 | 0,0253 |
| 24 | 94,78 | -0,0790 | 0,0062 |
| 25 | 94,91 | 0,0510 | 0,0026 |
| 26 | 94,89 | 0,0310 | 0,0010 |
| 27 | 94,76 | -0,0990 | 0,0098 |
| 28 | 94,8 | -0,0590 | 0,0035 |
| 29 | 94,95 | 0,0910 | 0,0083 |
| 30 | 95 | 0,1410 | 0,0199 |
| Сумма: | 0,0 | 0,8967 | |
Исходя из таблиц 2.7 и 2.8 рассчитывается значение критерия Шапиро – Уилка:
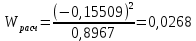
Расчетное значение критерия сравнивается с табличным значением, называемым критическим. Критическое значение критерия
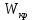 для n=30 и уровня значимости α=0,05 равно 0,927. В данном случае
для n=30 и уровня значимости α=0,05 равно 0,927. В данном случае 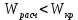 , это позволяет сделать вывод, что рассматриваемые значения подчиняются нормальному закону распределения.
, это позволяет сделать вывод, что рассматриваемые значения подчиняются нормальному закону распределения.
Кроме того, при числе результатов измерений n < 50 нормальность их распределения проверяют с помощью составного критерия.
Вычисляют отношение d по формуле (2.21):
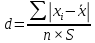 | (2.21) |
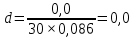
 Результаты измерений считают распределенными нормально, если соблюдается условие
Результаты измерений считают распределенными нормально, если соблюдается условие 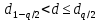 . Первый коэффициент при уровне значимости 0,05 равен 0,7404, второй коэффициент при уровне значимости 0,99 равен 0,8826. Значения взяты из справочной таблицы по ближайшему числу значений в выборке n = 31 (по варианту n = 30).
. Первый коэффициент при уровне значимости 0,05 равен 0,7404, второй коэффициент при уровне значимости 0,99 равен 0,8826. Значения взяты из справочной таблицы по ближайшему числу значений в выборке n = 31 (по варианту n = 30). Таким образом, условие принимает вид
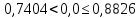 , это позволяет сказать, что выборка не подчиняется нормальному распределению.
, это позволяет сказать, что выборка не подчиняется нормальному распределению.Проверка соответствия выборки нормальному закону распределения показала, что по критерию Шапиро – Уилка выборка подчиняется этому закону, так как соблюдается необходимое условие
 (0,0268 < 0,927). При проверке выборки при помощи составного критерия было выяснено, что выборка не подчиняется закону нормального распределения, так как не соблюдается условие
(0,0268 < 0,927). При проверке выборки при помощи составного критерия было выяснено, что выборка не подчиняется закону нормального распределения, так как не соблюдается условие 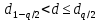 (
(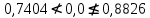 ).
).