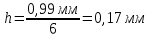Файл: Определение надежности технологической операции механической обработки детали упмбп. 19. 18.docx
Добавлен: 22.11.2023
Просмотров: 111
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
приведены в таблице 2.3.
Таблица 2.3 – Данные для вычисления теоретических частот
Полученные частоты в конце расчета округляются до целых. Далее необходимо вычислить величину χ2 по формуле 2.12 и обозначить ее через 
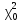. Расчет вести, пользуясь таблицей 2.4.
Таблица 2.4 – Расчет значений по критерию Пирсона
Продолжение таблицы 2.4
Таким образом, значение критерия Пирсона 
равно:
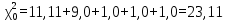
Далее находится число степеней свободы k (параметр распределения Пирсона) по формуле 2.13:
где g – число интервалов вариационного ряда,
r – сумма числа параметров теоретического закона распределения.
Для нормального распределения признака Х принято r = 3. Уровень значимости α = 0,95.
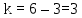
По найденному числу степеней свободы k и уровню значимости α, пользуясь таблицей критических точек распределения из учебного пособия В. И. Губина, необходимо определить критическое значение χкр2, которое составляет 0,352.
Так как > 
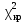(23,11 > 0,352), то по критерию Пирсона гипотеза о нормальном распределении признака Х отвергается.
Далее необходимо провести проверку близости эмпирического распределения к нормальному по критерию Романовского.
При этом методе по опытным данным выборки вычисляют характеристики распределения: среднее арифметическое значение 
и среднее квадратическое отклонение 
с предварительно исключенным из нее резко выделяющимся значением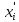 
.
Затем определяют величину квантиля по формуле (2.14):
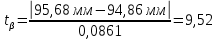
Задавшись процентом риска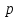
, при котором грубая ошибка может быть принята за случайную 
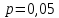, по таблице 2.3 в зависимости от объема выборки N находят критическое значение
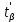, которое сравнивают с ранее вычисленным значением 
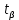по формуле (2.14).
Таблица 2.5 – Допустимые значения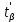 при 
Так как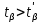
(9,52 > 2,08), то резко выделяющееся значение 
является грубой ошибкой и исключается из выборки.
Таким образом, по критерию Пирсона и по критерию Романовского закон о нормальном распределении отвергается, то есть нет существенных оснований считать, что эмпирическое распределение результатов замеров действительных размеров деталей подчиняется нормальному закону распределения.
Критерий «правило трех сигм», или критерий Райта, является одним из простейших для проверки результатов, подчиняющихся нормальному закону распределения, сущность которого заключается в следующем: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основания предполагать, что изучаемая величина распределена нормально. С этой целью для выборки вычисляется центр распределения и оценка СКО результата наблюдений.
Результат, который удовлетворяет условию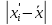 
3S считается имеющим грубую погрешность и удаляется, а ранее вычисленные характеристики распределения уточняются (где
– результат наблюдения, проверяемый на наличие грубой погрешности; - среднее арифметическое значение).
Подставив вычисленные ранее переменные в неравенство, можно сказать, что условие не выполняется:
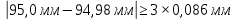
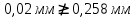
Проверка по критерию Райта доказывает, что максимальное значение из выборки также не является грубой погрешностью.
Согласно проверке на грубые погрешности измерений, по методу Грэббса резко выделяющееся значение (95,68 мм) исключается и производится пересчет уточненных характеристик распределения и Sx. По методу Ирвина результат не является ошибочным и не исключается, как и по критерию Райта. Проверка по критерию Романовского показывает, что распределение не моделируется нормальным распределением.
2.4 Определение закона распределения выборки
Для выявления и анализа закономерностей распределения характеристик качества обработанной партии заготовок на настроенных станках строят практические кривые распределения с последующей математической обработкой.
Вся совокупность размеров разбивается на несколько интервалов и определяется частность, то есть отношение числа деталей, размеры которых попали в данный интервал, к общему числу измеренных деталей данной партии.
По результатам измерения, определяется разность между наибольшим (rmax) и наименьшим (rmin) действительными размерами, которая называется размахом варьирования (R) и определяется по следующей формуле 2.15:
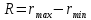(2.15)
где dmax – число, которое больше наибольшего значения выборки на 0,005 мм;
dmin – число, которое меньше наименьшего значения из выборки на 0,005мм.
Интервалы и границы интервалов выбираются таким образом, чтобы ни одно значение случайной величины не попало на границу интервала, для этого за нижнюю границу интервала принимаем число, меньше наименьшего значения из выборки на 0,005 мм, за верхнюю границу интервала принимаем число, больше наибольшего значения выборки на 0,005 мм.
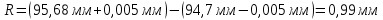
Определяем число интервалов варьирования по формуле 2.16:
где N – величина выборки.
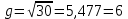
Далее производится расчет ширины интервалов по формуле 2.17:
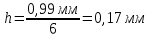
Таблица 2.3 – Данные для вычисления теоретических частот
| xi | xi –  |  |  |  |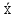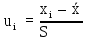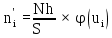
| 94,78 | -0,05 | -0,588 | 0,3352 | 9 |
| 94,95 | 0,12 | 1,385 | 0,1518 | 4 |
| 95,12 | 0,29 | 3,358 | 0,0014 | 1 |
| 95,29 | 0,46 | 5,332 | 0,0001 | 1 |
| 95,46 | 0,63 | 7,305 | 0,0001 | 1 |
| 95,63 | 0,80 | 9,279 | 0,0001 | 1 |
Полученные частоты
в конце расчета округляются до целых. Далее необходимо вычислить величину χ2 по формуле 2.12 и обозначить ее через 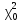. Расчет вести, пользуясь таблицей 2.4.Таблица 2.4 – Расчет значений по критерию Пирсона
| ni | | ni – | (ni – )2 |  |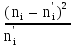
| 19 | 9 | 10 | 100 | 11,11 |
Продолжение таблицы 2.4
| ni | | ni – | (ni – )2 | |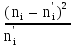
| 10 | 4 | 6 | 36 | 9 |
| 0 | 1 | -1 | 1 | 1 |
| 0 | 1 | -1 | 1 | 1 |
| 0 | 1 | -1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
Таким образом, значение критерия Пирсона равно: 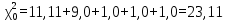Далее находится число степеней свободы k (параметр распределения Пирсона) по формуле 2.13:
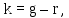 | (2.13) |
где g – число интервалов вариационного ряда,
r – сумма числа параметров теоретического закона распределения.
Для нормального распределения признака Х принято r = 3. Уровень значимости α = 0,95.
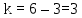
По найденному числу степеней свободы k и уровню значимости α, пользуясь таблицей критических точек распределения из учебного пособия В. И. Губина, необходимо определить критическое значение χкр2, которое составляет 0,352.
Так как
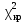> (23,11 > 0,352), то по критерию Пирсона гипотеза о нормальном распределении признака Х отвергается.Далее необходимо провести проверку близости эмпирического распределения к нормальному по критерию Романовского.
При этом методе по опытным данным выборки вычисляют характеристики распределения: среднее арифметическое значение и среднее квадратическое отклонение с предварительно исключенным из нее резко выделяющимся значением 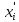. Затем определяют величину квантиля по формуле (2.14):
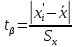 | (2.14) |
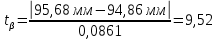
Задавшись процентом риска
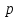, при котором грубая ошибка может быть принята за случайную 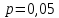, по таблице 2.3 в зависимости от объема выборки N находят критическое значение
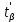, которое сравнивают с ранее вычисленным значением 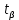по формуле (2.14).Таблица 2.5 – Допустимые значения
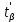при | N | 20 | 25 | 30 | 40 | 50 | 120 |
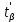| | 2,14 | 2,10 | 2,08 | 2,05 | 2,02 | 1,99 |
Так как
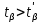(9,52 > 2,08), то резко выделяющееся значение является грубой ошибкой и исключается из выборки.Таким образом, по критерию Пирсона и по критерию Романовского закон о нормальном распределении отвергается, то есть нет существенных оснований считать, что эмпирическое распределение результатов замеров действительных размеров деталей подчиняется нормальному закону распределения.
Критерий «правило трех сигм», или критерий Райта, является одним из простейших для проверки результатов, подчиняющихся нормальному закону распределения, сущность которого заключается в следующем: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основания предполагать, что изучаемая величина распределена нормально. С этой целью для выборки вычисляется центр распределения и оценка СКО результата наблюдений.
Результат, который удовлетворяет условию 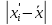3S считается имеющим грубую погрешность и удаляется, а ранее вычисленные характеристики распределения уточняются (где
– результат наблюдения, проверяемый на наличие грубой погрешности; - среднее арифметическое значение). Подставив вычисленные ранее переменные в неравенство, можно сказать, что условие не выполняется:
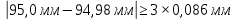
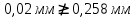
Проверка по критерию Райта доказывает, что максимальное значение из выборки также не является грубой погрешностью.
Согласно проверке на грубые погрешности измерений, по методу Грэббса резко выделяющееся значение (95,68 мм) исключается и производится пересчет уточненных характеристик распределения
и Sx. По методу Ирвина результат не является ошибочным и не исключается, как и по критерию Райта. Проверка по критерию Романовского показывает, что распределение не моделируется нормальным распределением.2.4 Определение закона распределения выборки
Для выявления и анализа закономерностей распределения характеристик качества обработанной партии заготовок на настроенных станках строят практические кривые распределения с последующей математической обработкой.
Вся совокупность размеров разбивается на несколько интервалов и определяется частность, то есть отношение числа деталей, размеры которых попали в данный интервал, к общему числу измеренных деталей данной партии.
По результатам измерения, определяется разность между наибольшим (rmax) и наименьшим (rmin) действительными размерами, которая называется размахом варьирования (R) и определяется по следующей формуле 2.15:
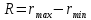(2.15)где dmax – число, которое больше наибольшего значения выборки на 0,005 мм;
dmin – число, которое меньше наименьшего значения из выборки на 0,005мм.
Интервалы и границы интервалов выбираются таким образом, чтобы ни одно значение случайной величины не попало на границу интервала, для этого за нижнюю границу интервала принимаем число, меньше наименьшего значения из выборки на 0,005 мм, за верхнюю границу интервала принимаем число, больше наибольшего значения выборки на 0,005 мм.
| | |
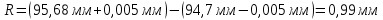
Определяем число интервалов варьирования по формуле 2.16:
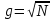 , | (2.16) |
| | |
где N – величина выборки.
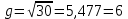
Далее производится расчет ширины интервалов по формуле 2.17: 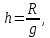 | (2.17) |