Критерий согласия Пирсона 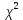– один из основных, который можно представить как сумму отношений квадратов расхождений между теоретическими ( 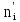) и эмпирическими (n_i) частотами к теоретическим
частотам (формула 1.1):

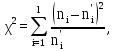(1.1)

Для распределения 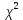составлены таблицы, где указано критическое значение критерия согласия для выбранного уровня значимости α и степеней свободы df (или ν). Уровень значимости α – вероятность того, что будет отвергнута правильная гипотеза. Р — статистическая достоверность принятия верной гипотезы. В статистике чаще всего пользуются тремя уровнями значимости:

1) α=0,10, тогда Р=0,90 (в 10 случаях из 100);

2) α=0,05, тогда Р=0,95 (в 5 случаях из 100);

3) α=0,01, тогда Р=0,99 (в 1 случае из 100) может быть отвергнута правильная гипотеза.

При полном совпадении теоретического и эмпирического распределений 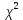=0, в противном случае 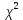>0. Если > 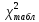, то при заданном уровне значимости и числе степеней свободы гипотеза о несущественности (случайности) расхождений отклоняется. В обратном случае гипотеза принимается и с вероятностью Р = (1 - α) можно утверждать, что расхождение между теоретическими и эмпирическими частотами случайно. Следовательно, есть основания утверждать, что эмпирическое распределение подчиняетсянормальному распределению. 

Критерий согласия Пирсона используется, если объем совокупности достаточно велик (N>50), при этом, частота каждой группы должна быть не менее 5.

Критерий согласия Колмогорова предназначен для проверки гипотезы о принадлежности выборки некоторому закону распределения, то есть проверки того, что эмпирическое распределение соответствует предполагаемой модели.

Критерий согласия Колмогорова основан на определении максимального расхождения между накопленными эмпирическими и теоретическими частотами (формула 1.2):

---

(1.2)

где D и d – соответственно, максимальная разность между накопленными частотами и накопленными частостями эмпирического и теоретического распределений.
По таблице распределения статистики Колмогорова определяют вероятность, которая может изменяться от 0 до 1. При Р(λ)=1 – происходит полное совпадение частот, Р(λ)=0 – полное расхождение. Если величина вероятности Р значительна по отношению к найденной величине λ, то можно предположить, что расхождения между теоретическим и эмпирическим распределениями несущественны, т. е. носят случайный характер. Основное условие использования критерия Колмогорова – достаточно большое число наблюдений.

Критерий Шапиро – Уилка является специальным критерием нормальности и используется для проверки гипотезы о нормальном распределении. Этот критерий надёжен при 8 ≤ n ≤ 50.

При использовании критерия Шапиро – Уилка результаты испытаний располагают в вариационный ряд. Расчётное значение критерия получают по формуле (1.3):

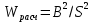(1.3)

где 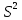 - сумма квадратов отклонений значений выборки от среднего арифметического.

Значение B² находят по формуле (1.4):

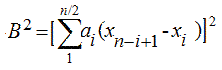(1.4)

где i – номер элемента в вариационном ряду

a_i – табличный коэффициент.

Рассчитанное значение 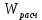сравнивают с табличным 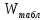. Если 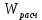> 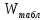, то гипотезу нормальности распределения не отвергают
(принимают на заданном уровне значимости α).

В данной работе рассмотрены только основные критерии согласия и способы их определения.

---

При проверке на однородность при помощи третьей группы статистических критериев (критерии проверки на однородность) случайные величины исследуются на факт значимости различия их законов распределения (то есть проверки того, подчиняются ли эти величины одному и тому же закону). Используются в факторном анализе для определения наличия зависимостей.

Также существует классификация критериев на следующие группы:

1) параметрические;

2) непараметрические.

Параметрическими называют критерии, которые основаны на предположении, что распределение признака в совокупности подчиняется некоторому известному закону. К этой группе критериев относятся такие критерии, как t – критерий Стьюдента, критерий Фишера, критерий отношения правдоподобия, критерий Романовского.

Критерий t Стьюдента направлен на оценку различий величин средних X и У двух выборок X и У, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних связных и несвязных выборок, причем выборки могут быть не равны по величине.

Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух независимых выборок. Для вычисления 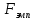нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Если 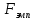> 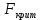, то нулевая гипотеза принимается, в противном случае принимается альтернативная.

В.И. Романовский предложил более простой метод оценки близости эмпирического распределения к нормальному, используя величину   он предложил вычислять отношение (формула 1.5):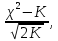

(1.5)

где К – число степеней свободы.

---

Если это отношение по абсолютной величине меньше трех, то расхождение между эмпирическим и теоретическим распределениями считается несущественным; если же это отношение по абсолютной величине больше трех, то расхождение существенно. Несущественность расхождения говорит о возможности принять за закон данного эмпирического распределения нормальное распределении.

Таким образом, статистическая проверка гипотез проводится с помощью некоторого статистического критерия по общей логической схеме, включающей нахождение конкретного вида функции от результатов наблюдения (критической статистики), на основании которой принимается окончательное решение. Например, могут рассматриваться гипотезы об общем законе распределения исследуемой случайной величины, об однородности двух или нескольких обрабатываемых выборок, о числовых значениях параметров исследуемой генеральной совокупности и др. Результат проверки может быть либо отрицательным, либо неотрицательным. В первом случае гипотеза ошибочна, во втором – ее нельзя считать доказанной: просто она не противоречит имеющимся выборочным данным, однако таким же свойством могут наряду с ней обладать и другие гипотезы. Для статистической проверки гипотез используются разные критерии. В частности, когда проверяется согласие между выборочным и гипотетическим распределениями, используется критерий согласия, например, критерий Пирсона «хи – квадрат», критерий Колмогорова – Смирнова и др.

2 Определение надежности технологической операции
Для определения надежности технологической операции механической обработки вала применяются размеры из задания на курсовую работу. Для расчетов надежности необходимо определить закон распределения выборки, произвести расчет основных математических характеристик, оценить грубые погрешности измерений и обработки, а также определить процент брака.

---

2.1 Определение основных математических характеристик случайной величины
Для оценки точности и стабильности технологического процесса применяется статистический метод, основной целью которого является получение и обработка систематизированной непрерывной информации о качестве продукции, необходимой для дальнейшего совершенствования технологического процесса.

Методика статистического анализа предполагает оценку основных параметров и сопоставление оценок и распределений с нормативными параметрами и допусками. Определяем допуск на исполнительный параметр по следующий формуле:

Определяем допуск на исполнительный параметр по следующей формуле (2.1):

,

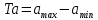(2.1)

где a_max – максимальный предельный размер;


a_min – минимальный предельный размер.

Причем, максимальный и минимальный предельные размеры определяются по формуле (2.2) и (2.3) соответственно.

,

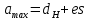(2.2)

где d_н – номинальный диаметр контролируемого вала,

es – верхнее предельное отклонение вала.

,

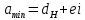(2.3)

где d_н – номинальный диаметр контролируемого вала,

ei –нижнее предельное отклонение вала.
Предельные отклонения находятся по справочнику Мягкова. Верхнее предельное отклонение вала равно 0 мм. Нижнее предельное отклонение вала составляет -0,35 мм.





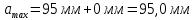
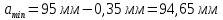
Исходя из расчетов определяем допуск на исполнительный параметр.



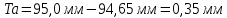
Основными параметрами, характеризующими закон нормального распределения (закон Гаусса), являются среднеарифметическое значение и среднеквадратическое отклонение. Так как среднеарифметическое значение будет являться несмещённой оценкой математического ожидания (среднее значение, одна из важнейших характеристик распределения вероятностей случайной величины), а среднеквадратическое отклонение наиболее употребительная мера рассеяния.

---

Смотрите также файлы

• Теоретические основы управления персоналом в условиях кризиса 4.docx

• Сценарий классного часа До свидания, 1 класс!.docx

• Алгоритмдеу жне программалау Педагогты атыжні.docx

• Кгэу министерство науки и высшего образования российской федерации федеральное государственное бюджетное образовательное учреждение высшего образования.docx

• язык и речь.docx