https://www.muctr.ru/upload/iblock/059/Lektsiya6.pdf константы и инварианты подробно

5. Гидростатика. Диф. уравнения равновесия Эйлера. Основное уравнение гидростатики.

В гидростатике изучается равновесие жидкостей, находящихся, в общем случае, в состоянии относительного покоя, при котором в движущейся жидкости ее частицы не перемещаются друг относительно друга. При этом силы внутреннего трения отсутствуют, что позволяет считать жидкость идеальной.

В состоянии относительного покоя форма объема жидкости не изменяется, и она, подобно твердому телу, перемещается как единое целое.

На неподвижную жидкость действуют поверхностные и массовые силы. В результате действия этих сил в жидкости возникает напряжение сжатия называемое гидростатическим давлением или просто давлением. Силы гидростатического давления, возникающего в жидкости, приводят к сохранению ее равновесия. Давление жидкости у поверхности раздела определяют по формуле

_,

где р – гидростатическое давление,

F – поверхностная сила давления,

S – площадь поверхности раздела.

Это выражение называется системой дифференциальных уравнений Эйлера для покоящейся жидкости.

Разделив все уравнения на плотность   и умножив первое уравнение на  , второе на 

---

 и третье на   после сложения уравнений, получим:

,

т.к. давление является только функцией координат, то выражение  есть полный дифференциал – dp.

,

где 

Приращение давления при изменении координат согласно уравнению Эйлера составляет:



полученное уравнение является основным уравнением гидростатики в дифференциальной форме
6. Практическое применение основного уравнения гидростатики.

1) Принцип сообщающихся сосудов и его использование.

Пусть два открытых сообщающихся сосуда заполнены жидкостью плотностью ρ (рисунок 5а).

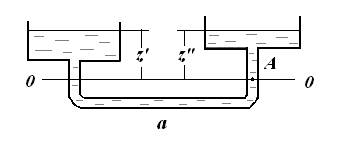а) сосуды заполнены однородной жидкостью ( ), б) сосуды заполнены неоднородной жидкостью ( ), Рисунок 5 - Сообщающиеся сосуды

Выберем произвольную плоскость сравнения 0-0 и некоторую точку А внутри жидкости, лежащую в этой плоскости. Если считать точку А принадлежащей левому сосуду, то, согласно закону Паскаля давление в этой точке:

,

Если же считать точку А принадлежащей правому сосуду, то давление в ней:

,

При равновесии для каждой точки давление одинаково в любом направлении (в противном случае происходило бы перемещение жидкости).

---

Следовательно:

<sub>,

Или  ,</sub>

Аналогичный вывод может быть сделан для двух закрытых сообщающихся сосудов, в которых давления над свободной поверхностью жидкости одинаковы.

Таким образом, в открытых или закрытых находящихся под одинаковым давлением сообщающихся сосудах, заполненных однородной жидкостью, уровни ее располагаются на одной высоте независимо от формы и поперечного сечения сосудов.

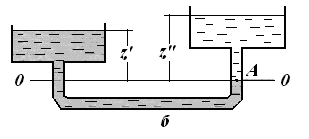
Если сообщающиеся сосуды заполнены двумя несмешивающимися жидкостями, имеющими плотность ρ’ (левый сосуд) и ρ’’ (правый сосуд), то при проведении плоскости сравнения 0-0 через границу раздела жидкостей (рисунок 5 б) аналогично предыдущему получим:



_{или  ,}

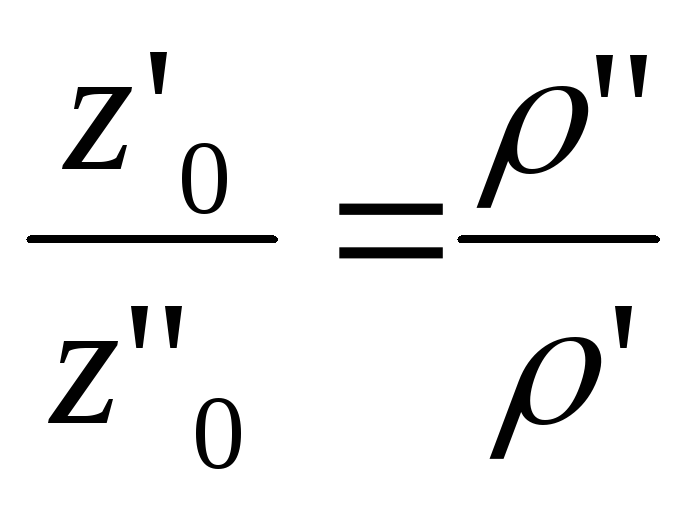Отсюда следует, что в сообщающихся сосудах высоты уровней разнородных жидкостей над поверхностью их раздела обратно пропорциональны плотностям этих жидкостей.

Если сосуды заполнены одной жидкостью плотностью ρ, но давление над уровнем жидкости в них неодинаковы и равны p’ (левый сосуд) и p” (правый сосуд) (рисунок 6):



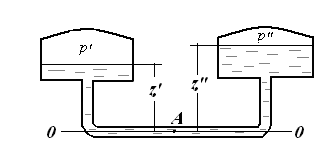
Рисунок 6 - Сообщающиеся сосуды, когда сосуды заполнены однородной жидкостью, но давление в сосудах разное ( )

то можно записать:

,

Откуда разность уровней жидкости в сосудах:

_,

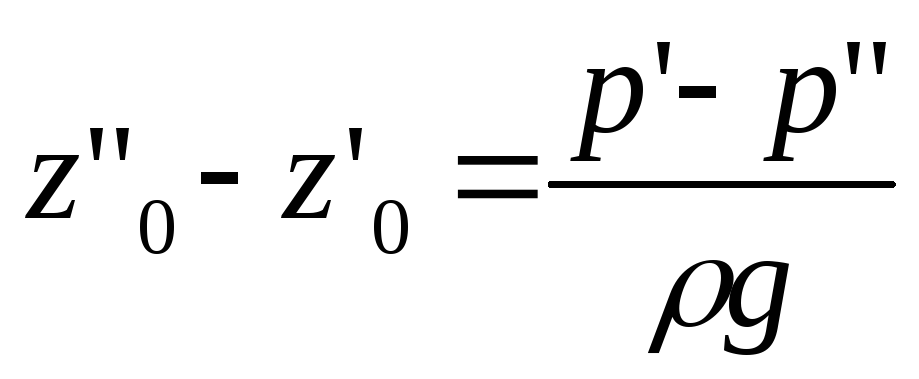Последнее уравнение применяется при измерении давлений или разностей давлений между различными точками с помощью дифференциальных U – образных манометров.

Условия равновесия жидкостей в сообщающихся сосудах используют также для определения высоты гидравлического затвора в различных аппаратах [2].

---

2) Пневматическое измерение уровня жидкости в резервуаре.

Для контроля за объемом жидкости в каком-либо резервуаре 1 например подземном (рисунок 6), в него помещают трубу 2, нижний конец которой доходит почти до днища резервуара.



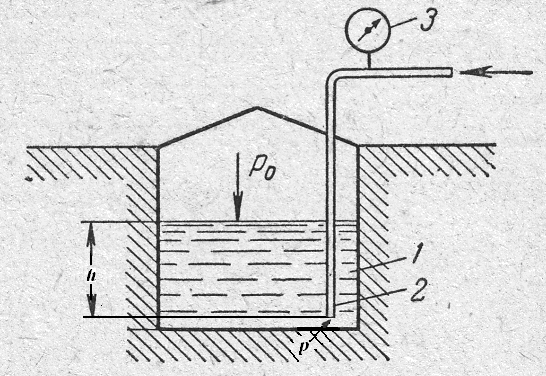
Рисунок 7 – Пневматический измеритель уровня жидкости

Давление над жидкостью в резервуаре равно р₀.

По трубе 2 подают сжатый воздух (газ) постепенно повышая его давление, замеряемое манометром 3.

Когда воздух преодолеет сопротивление столба жидкости в резервуаре и начнет барботировать сквозь жидкость, давление р, фиксируемое манометром, перестанет возрастать и будет равно:

,

Откуда уровень жидкости в резервуаре:

_,

По величине h и известной площади поперечного сечения резервуара определяют объем находящейся в нем жидкости 
7. Основные характеристики движения жидкости. Закон внутреннего трения Ньютона. Способы определения реологических свойств жидкостей.

При движении жидкости через сечение любой формы, отличной от круглой, в качестве расчетного линейного размера принимают гидравлический радиус или эквивалентный диаметр.

Под гидравлическим радиусом r_г (м) принимают отношение площади затопленного сечения трубопровода или канала, через которое протекает жидкость, т.е. живого сечения потока, к смоченному периметру:

_,

где S – площадь сечения потока жидкости, м²;

П – смоченный периметр, м.

Смоченный периметр П- часть периметра живого сечения, ограниченное твердыми стенками (рисунок 15, выделен двойной линией).

---

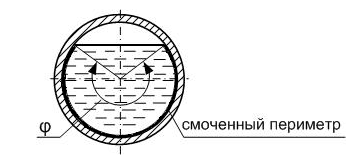
Рисунок 15 - Смоченный периметр

Для круглой трубы

_,

Для круглой трубы с внутренним диаметром d и, значит, площадью свободного сечения   <sub>при сплошном заполнении его жидкостью  , откуда гидравлический радиус:

,</sub>

Диаметр, выраженный через гидравлический радиус, представляет собой эквивалентный диаметр:

_,

Следовательно:

_,

Скорость и расход жидкости

Рассмотрим движение жидкости по трубе постоянного сечения.

Количество жидкости, протекающей через поперечное сечение потока («живое сечение», т.е. затопленное сечение трубопровода (рисунок 16)) в единицу времени, называют расходом жидкости.



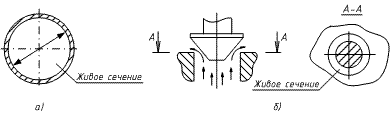
Рисунок 16 - Живые сечения: а - трубы, б - клапана

Различают Q - объемный расход [м³/с], и массовый расход М [кг/с].

В разных точках живого сечения потока скорость частиц жидкости неодинакова. Поэтому в расчетах используют не истинные (локальные) скорости, а фиктивную среднюю скорость.

Средняя скорость  – выражается отношением объемного расхода жидкости к площади живого сечения потока [1,3,4].

_,

где Q - объемный расход, м³/с;

S – площадь живого сечения, м².

Откуда объемный расход:

_,

Массовый расход 

---

Смотрите также файлы

• Детский сад на базе Института педагогики.docx

• Тема Экономическая безопасность.docx

• Основы взаимодействия воспитателя с родителями (лицами, их заменяющими) и сотрудниками дошкольной образовательной организации.pdf

• Вопросы Что понимает закон под эмансипацией гражданина В каком порядке она осуществляется.docx

• Общество массового потребления информации. Тезисы выступления на iv академических чтениях, посвященных памяти проф. Г. И. Волынки Философия, образование, наука в глобальном измерении социальнотурбулентного мира.docx