ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 90
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М [кг/с ]:
 ,
,
где ρ – плотность жидкости кг/м3.
ИЛИ Основными параметрами, характеризующими движение жидкости являются: площадь живого сечения S, расход жидкости Q и средняя скорость движения v.
Площадь живого сечения. Живым сечением потока жидкости рисунок 1 называется сечение, которое в каждой своей точке нормально к векторам скоростей частиц жидкости.
В практике чаще всего встречаются потоки жидкостей, живое сечение которых представляет собой поверхность, мало отличающуюся от плоскости.
Расход жидкости. Расходом жидкости называется количество жидкости, проходящее через данное живое сечение единицу времени. Расход может измеряться в объемных или массовых единицах:
Средняя скорость движения жидкости. В общем случае скорости частиц в разных точках живого сечения будут различны. Если площадь эпюры частных скоростей Fэ разделить на ширину потока жидкости H, то в соответствующем масштабе получим значение средней скорости движения жидкости, т.е.
Закон Ньютона: Площадь соприкасающихся в относительном перемещении поверхностей и градиент скорости жидкости между ними прямо пропорциональны силе вязкого трения.
В настоящее время для определения реологических характеристик рабочих жидкостей, используемых в машиностроении, широко применяют два способа [1–4]. 1. Прямое определение связи напряжения сдвига от скорости сдвига путем приложения к образцу однородного сдвига в специально сконструированном приборе. Вискозиметры, использующие данный принцип, представляют собой ротационные устройства в виде соосных цилиндров или конуса и пластины. 2. Установление зависимости между напряжением и скоростью сдвига косвенным способом – по измерениям перепада давлений и расхода жидкости в прямолинейном канале или вискозиметрах с капиллярной трубкой. В приборах данного типа скорость сдвига не постоянна поперек канала, а изменяется от нуля на оси канала до максимального своего значения на стенке. Как следствие, результаты, полученные при указанном способе, определяются их интерпретацией и не являются очевидными
8. Режимы движения жидкостей. Механизмы ламинарного и турбулентного движения. Гидродинамический пограничный слой.
При низких скоростях движения частиц жидкости в потоке преобладают силы трения, числа Рейнольдса малы. Такое движение называется
ламинарным.
При высоких скоростях движения частиц жидкости в потоке числа Рейнольдса велики, тогда в потоке преобладают силы инерции и эти силы определяют кинематику и динамику частиц, такой режим называется турбулентным
Рассмотрим процесс продольного смывания какого-либо тела безграничным потоком жидкости с постоянной скоростью течения w (рис. 1). Вследствие влияния сил трения в непосредственной близости от поверхности тела скорость течения должна очень быстро падать до нуля. Тонкий слой жидкости вблизи поверхности тела, в котором происходит изменение скорости жидкости от значения скорости невозмущенного потока вдали от стенки до нуля непосредственно на стенке, называется гидродинамическим пограничным слоем (рис. 1). Толщина этого слоя δ возрастает вдоль по потоку.
С увеличением скорости потока толщина динамического пограничного слоя уменьшается вследствие сдувания его потоком. Напротив, с увеличением вязкости толщина динамического слоя увеличивается. Течение в динамическом пограничном слое может быть как турбулентным 1, так и ламинарным 2 (рис.2). Характер течения и толщина в нем (δл и δТ) определяются в основном величиной числа Re.
Необходимо отметить, что в случае турбулентного динамического пограничного слоя непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором имеет ламинарный характер. Этот слой называют вязким, или ламинарным, подслоем.
9. Уравнение расхода и неразрывности потока. Способы расчета и определения расхода жидкостей.
Расходом называется количество жидкости, протекающее через живое сечение потока в единицу времени.
Объемный - Q=V*S, (м3/с);
Массовый - Qm=ρV*S, (кг/с);
Весовой - QG=ρg*Q, (Н/с);
где V- мгновенная скорость в данной точке,δS– площадь сечения струйки.
Условие неразрывности потока основывается на законе сохранения вещества.
А также на следующих допущениях:
а) трубка тока имеет свойство непроницаемости для внешних, обтекающих ее потоков;
б) предположение о сплошности (неразрывности) среды для установившегося течения несжимаемой жидкости.
На этих основаниях можно утверждать, что объемный расход во всех сечениях элементарной струйки (см. рис.5.2) один и тот же.
Уравнениенеразрывностидля потока,ограниченного непроницаемыми стенками (уравнение расхода для потока).
Q = Vср1 *S1 = Vср2 *S2 →const(вдоль потока), (5.6’)
где Vср1 , Vср2 - средние скорости.
10. Выбор оптимального диаметра трубопроводов. Расход энергии на перемещение жидкостей.
Оптимальный диаметр трубопровода может быть найден на основе технико-экономических расчетов. Размеры трубопровода, включая размеры и функциональные возможности различных компонентов, а также условия, при которых должна происходить эксплуатация трубопровода, определяет транспортирующая способность системы. Трубы большего размера подходят для более интенсивного массового потока среды Оптимальный размер – наименьший из подходящих размеров трубы для конкретного применения, экономически эффективный на протяжении всего срока службы системы.
Формула для расчета производительности трубы:
Q = (π·d²)/4 · v
Q – расход перекачиваемой жидкости;
d – диаметр трубопровода;
v – скорость потока.
11. Уравнение движения реальной жидкости. Гидродинамические критерии подобия. Упрощенное уравнение Навье-Стокса.

На практике не всегда удается создать точную модель, динамически подобную натуре, т.к. судить о динамическом подобии двух систем путем измерения и сравнения между собой действующих в них сил не всегда возможно. Поэтому соотношение сил, действующих в натуре и в модели может быть установлено косвенным путем по соотношению величин, поддающихся измерению. Тогда пользуются критериями динамического подобия, учитывающими только основные силы, определяющие характер гидравлических процессов и когда в качестве преобладающей принимается какая-нибудь одна (главенствующая) из действующих сил.
Критерий Фруда
Если преобладает действие сил тяжести, то необходимо выполнение условия, вытекающего из зависимости:
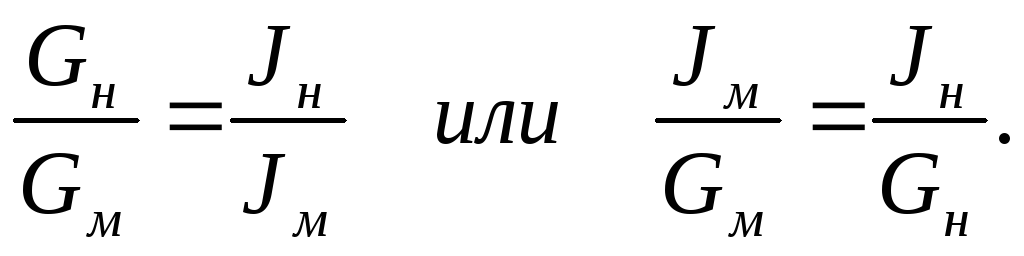
С учетом вышеизложенного:
 - число Фруда.
- число Фруда.
Или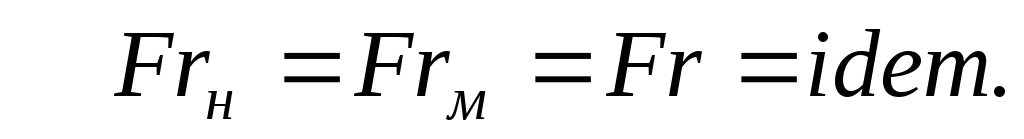
Критерий Рейнольдса
При преобладающем действии сил трения необходимо выполнение условия, вытекающего из зависимости аF=const.
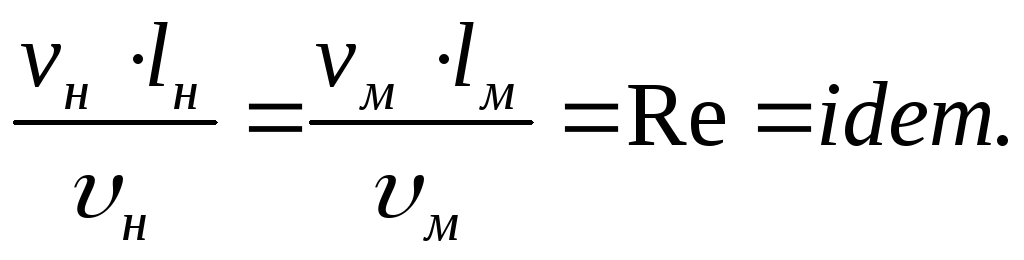
Или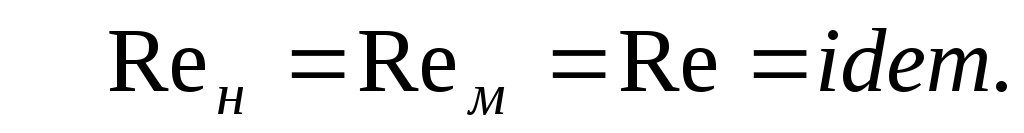
Критерий Эйлера
Если преобладает действие сил давления, то необходимо выполнять условие по аналогии с предыдущим:
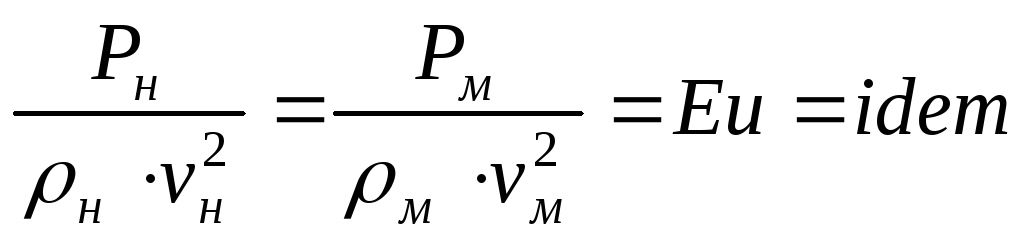
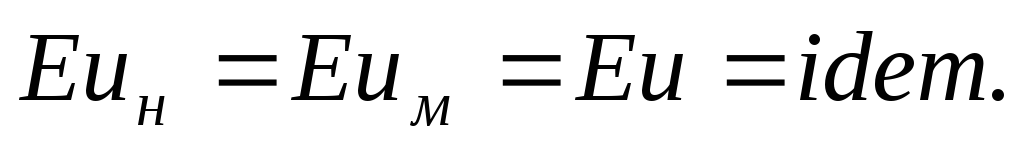
При соблюдении критерия Рейнольдса критерий Эйлера выполняется автоматически, и тогда

Существует ещё целый ряд критериев Вебера (если преобладают силы поверхностного натяжения), Струхаля (если преобладают силы инерции в условиях неустановившегося движения), Маха (при преобладающем влиянии сжимаемости жидкости), Архимеда (при действии Архимедовых сил из-за разности плотности двух сред), Коши (если преобладает действие упругих сил (гидроудар)), Лагранжа, Прандтля, Ричардсона и др.
12. Уравнение Бернулли для идеальных и реальных жидкостей.
z1 + (p1/ρg) + (V12/2g) = z2 + (p2/ρg) + (V22/2g)
Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.
В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока
Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора Δh составят:
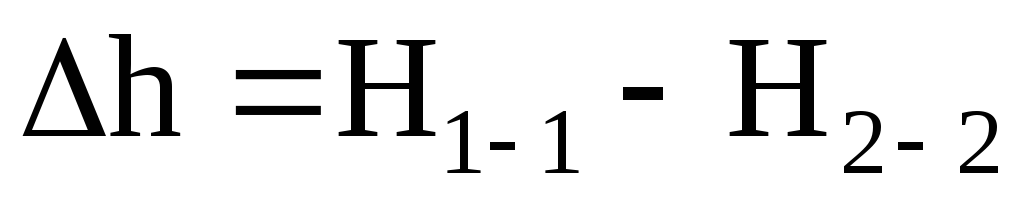 ,
,
где H1-1- напор в первом сечении потока жидкости,
H2-2 - напор во втором сечении потока,
∆h - потерянный напор - энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.
С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть

13. Практическое применение уравнения Бернулли. Истечение жидкости через отверстия.
Уравнение Бернулли находит самое широкое применение в технике. Работа ряда устройств и приборов основана на использовании этого важнейшего закона гидравлики. На основании уравнения Бернулли создан ряд приборов: водомер Вентури, водоструйный насос, эжектор, карбюратор и т. д. Рассмотрим некоторые из них.
Карбюратор. Карбюратор предназначен для образования рабочей смеси топлива в поршневых двигателях внутреннего сгорания, т. е. для подсоса бензина и смешивания его с воздухом.
Струйный насос. Струйный насос нашел широкое применение в технике. Иногда его называют эжектором. На рис. 2.14 представлена схема струйного насоса. Он состоит из двух насадок: сходящегося 7, в котором происходит сжатие рабочего потока Ql воздуха или жидкости и увеличение его скорости, и постепенно расширяющегося насадка 2, расположенного в камере 3. Вследствие увеличения скорости потока давление в струе и во всей камере, согласно закону Бернулли, уменьшается. В связи с этим атмосферное давление /?атм, которое постоянно воздействует на свободную поверхность жидкости, поднимает ее (поток Q2) по патрубку 4 в камеру 3, где она подхватывается рабочим потоком жидкости (воздуха) и направляется в расширяющийся насадок. Здесь скорость постепенно снижается, а давление возрастает до атмосферного. Струйные насосы применяются в жидкостных реактивных двигателях.
Трубчатый расходомер Вентури.
где ρ – плотность жидкости кг/м3.
ИЛИ Основными параметрами, характеризующими движение жидкости являются: площадь живого сечения S, расход жидкости Q и средняя скорость движения v.
Площадь живого сечения. Живым сечением потока жидкости рисунок 1 называется сечение, которое в каждой своей точке нормально к векторам скоростей частиц жидкости.
В практике чаще всего встречаются потоки жидкостей, живое сечение которых представляет собой поверхность, мало отличающуюся от плоскости.
Расход жидкости. Расходом жидкости называется количество жидкости, проходящее через данное живое сечение единицу времени. Расход может измеряться в объемных или массовых единицах:
Средняя скорость движения жидкости. В общем случае скорости частиц в разных точках живого сечения будут различны. Если площадь эпюры частных скоростей Fэ разделить на ширину потока жидкости H, то в соответствующем масштабе получим значение средней скорости движения жидкости, т.е.
Закон Ньютона: Площадь соприкасающихся в относительном перемещении поверхностей и градиент скорости жидкости между ними прямо пропорциональны силе вязкого трения.
В настоящее время для определения реологических характеристик рабочих жидкостей, используемых в машиностроении, широко применяют два способа [1–4]. 1. Прямое определение связи напряжения сдвига от скорости сдвига путем приложения к образцу однородного сдвига в специально сконструированном приборе. Вискозиметры, использующие данный принцип, представляют собой ротационные устройства в виде соосных цилиндров или конуса и пластины. 2. Установление зависимости между напряжением и скоростью сдвига косвенным способом – по измерениям перепада давлений и расхода жидкости в прямолинейном канале или вискозиметрах с капиллярной трубкой. В приборах данного типа скорость сдвига не постоянна поперек канала, а изменяется от нуля на оси канала до максимального своего значения на стенке. Как следствие, результаты, полученные при указанном способе, определяются их интерпретацией и не являются очевидными
8. Режимы движения жидкостей. Механизмы ламинарного и турбулентного движения. Гидродинамический пограничный слой.
При низких скоростях движения частиц жидкости в потоке преобладают силы трения, числа Рейнольдса малы. Такое движение называется
ламинарным.
При высоких скоростях движения частиц жидкости в потоке числа Рейнольдса велики, тогда в потоке преобладают силы инерции и эти силы определяют кинематику и динамику частиц, такой режим называется турбулентным
-
При числах Рейдольдса ниже 2300 можно говорить о ламинарном движении частиц (в некоторых источниках указывается цифра 2000) -
Если критерий Рейнольдса больше 4000, то режим течения - турбулентный -
Числа Рейднольдса от 2300 до 4000 свидетельствуют о переходном режиме течения жидкости
Рассмотрим процесс продольного смывания какого-либо тела безграничным потоком жидкости с постоянной скоростью течения w (рис. 1). Вследствие влияния сил трения в непосредственной близости от поверхности тела скорость течения должна очень быстро падать до нуля. Тонкий слой жидкости вблизи поверхности тела, в котором происходит изменение скорости жидкости от значения скорости невозмущенного потока вдали от стенки до нуля непосредственно на стенке, называется гидродинамическим пограничным слоем (рис. 1). Толщина этого слоя δ возрастает вдоль по потоку.
С увеличением скорости потока толщина динамического пограничного слоя уменьшается вследствие сдувания его потоком. Напротив, с увеличением вязкости толщина динамического слоя увеличивается. Течение в динамическом пограничном слое может быть как турбулентным 1, так и ламинарным 2 (рис.2). Характер течения и толщина в нем (δл и δТ) определяются в основном величиной числа Re.
Необходимо отметить, что в случае турбулентного динамического пограничного слоя непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором имеет ламинарный характер. Этот слой называют вязким, или ламинарным, подслоем.
9. Уравнение расхода и неразрывности потока. Способы расчета и определения расхода жидкостей.
Расходом называется количество жидкости, протекающее через живое сечение потока в единицу времени.
Объемный - Q=V*S, (м3/с);
Массовый - Qm=ρV*S, (кг/с);
Весовой - QG=ρg*Q, (Н/с);
где V- мгновенная скорость в данной точке,δS– площадь сечения струйки.
Условие неразрывности потока основывается на законе сохранения вещества.
А также на следующих допущениях:
а) трубка тока имеет свойство непроницаемости для внешних, обтекающих ее потоков;
б) предположение о сплошности (неразрывности) среды для установившегося течения несжимаемой жидкости.
На этих основаниях можно утверждать, что объемный расход во всех сечениях элементарной струйки (см. рис.5.2) один и тот же.
Уравнениенеразрывностидля потока,ограниченного непроницаемыми стенками (уравнение расхода для потока).
Q = Vср1 *S1 = Vср2 *S2 →const(вдоль потока), (5.6’)
где Vср1 , Vср2 - средние скорости.
10. Выбор оптимального диаметра трубопроводов. Расход энергии на перемещение жидкостей.
Оптимальный диаметр трубопровода может быть найден на основе технико-экономических расчетов. Размеры трубопровода, включая размеры и функциональные возможности различных компонентов, а также условия, при которых должна происходить эксплуатация трубопровода, определяет транспортирующая способность системы. Трубы большего размера подходят для более интенсивного массового потока среды Оптимальный размер – наименьший из подходящих размеров трубы для конкретного применения, экономически эффективный на протяжении всего срока службы системы.
Формула для расчета производительности трубы:
Q = (π·d²)/4 · v
Q – расход перекачиваемой жидкости;
d – диаметр трубопровода;
v – скорость потока.
11. Уравнение движения реальной жидкости. Гидродинамические критерии подобия. Упрощенное уравнение Навье-Стокса.

На практике не всегда удается создать точную модель, динамически подобную натуре, т.к. судить о динамическом подобии двух систем путем измерения и сравнения между собой действующих в них сил не всегда возможно. Поэтому соотношение сил, действующих в натуре и в модели может быть установлено косвенным путем по соотношению величин, поддающихся измерению. Тогда пользуются критериями динамического подобия, учитывающими только основные силы, определяющие характер гидравлических процессов и когда в качестве преобладающей принимается какая-нибудь одна (главенствующая) из действующих сил.
Критерий Фруда
Если преобладает действие сил тяжести, то необходимо выполнение условия, вытекающего из зависимости:
С учетом вышеизложенного:
Или
Критерий Рейнольдса
При преобладающем действии сил трения необходимо выполнение условия, вытекающего из зависимости аF=const.
Или
Критерий Эйлера
Если преобладает действие сил давления, то необходимо выполнять условие по аналогии с предыдущим:
При соблюдении критерия Рейнольдса критерий Эйлера выполняется автоматически, и тогда
Существует ещё целый ряд критериев Вебера (если преобладают силы поверхностного натяжения), Струхаля (если преобладают силы инерции в условиях неустановившегося движения), Маха (при преобладающем влиянии сжимаемости жидкости), Архимеда (при действии Архимедовых сил из-за разности плотности двух сред), Коши (если преобладает действие упругих сил (гидроудар)), Лагранжа, Прандтля, Ричардсона и др.
12. Уравнение Бернулли для идеальных и реальных жидкостей.
z1 + (p1/ρg) + (V12/2g) = z2 + (p2/ρg) + (V22/2g)
-
где z - геометрическая высота, -
p - давление в выбранном сечении, -
V - скорость жидкости в выбранном сечении, -
ρ - плотность жидкости, -
g - ускорение свободного падения.
Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.
В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока
Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора Δh составят:
где H1-1- напор в первом сечении потока жидкости,
H2-2 - напор во втором сечении потока,
∆h - потерянный напор - энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.
С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть
13. Практическое применение уравнения Бернулли. Истечение жидкости через отверстия.
Уравнение Бернулли находит самое широкое применение в технике. Работа ряда устройств и приборов основана на использовании этого важнейшего закона гидравлики. На основании уравнения Бернулли создан ряд приборов: водомер Вентури, водоструйный насос, эжектор, карбюратор и т. д. Рассмотрим некоторые из них.
Карбюратор. Карбюратор предназначен для образования рабочей смеси топлива в поршневых двигателях внутреннего сгорания, т. е. для подсоса бензина и смешивания его с воздухом.
Струйный насос. Струйный насос нашел широкое применение в технике. Иногда его называют эжектором. На рис. 2.14 представлена схема струйного насоса. Он состоит из двух насадок: сходящегося 7, в котором происходит сжатие рабочего потока Ql воздуха или жидкости и увеличение его скорости, и постепенно расширяющегося насадка 2, расположенного в камере 3. Вследствие увеличения скорости потока давление в струе и во всей камере, согласно закону Бернулли, уменьшается. В связи с этим атмосферное давление /?атм, которое постоянно воздействует на свободную поверхность жидкости, поднимает ее (поток Q2) по патрубку 4 в камеру 3, где она подхватывается рабочим потоком жидкости (воздуха) и направляется в расширяющийся насадок. Здесь скорость постепенно снижается, а давление возрастает до атмосферного. Струйные насосы применяются в жидкостных реактивных двигателях.
Трубчатый расходомер Вентури.