ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 95
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Этот измерительный прибор имеет ряд достоинств. Он прост в изготовлении и эксплуатации (в нем отсутствуют какие-либо движущиеся части), имеет низкую стоимость, характеризуется незначительными потерями напора. Прибор можно использовать для измерения расхода как однородных, так и неоднородных жидкостей, широко применяется в лабораторных и промышленных условиях.
Гидродинамические трубки. Гидродинамические трубки предназначены для измерения местных скоростей в отдельных точках живого сечения потока жидкости.
Простейшей гидродинамической трубкой является трубка Пито. Трубка Пито изогнута под прямым углом и устанавливается в потоке навстречу течению жидкости. Если трубка установлена в открытом потоке, где на свободной поверхности жидкости давление равно атмосферному, то высота поднятия жидкости в трубке над поверхностью потока будет соответствовать скоростному напору.
Если жидкость движется в напорном трубопроводе, то для измерения скорости используется усовершенствованная трубка Пито—Прандтля. совершенствованная трубка Прандтля позволяет измерять скоростной и пьезометрический напоры. Прибор представляет собой хорошо обтекаемый цилиндр с концентрически расположенными в нем трубками. Приемником полного давления является отверстие осевого канала, а приемником пьезометрического напора — канавки на боковой поверхности цилиндра.
Помещая трубку Прандтля в различные точки поперечного сечения потока жидкости или воздуха, можно найти распределение скоростей в этом сечении и затем вычислить значение расхода. Трубку Прандтля можно также использовать в качестве датчика для измерения скорости полета самолета и других аппаратов.
Задача об истечении жидкости через отверстия - одна из основных в гидравлике и решается она уже две тысячи лет, восходя к Герону Александрийскому. Решение ее сводится к определению скорости истечения и расхода вытекающей жидкости. Этот случай движения характеризуется тем, что в процессе истечения запас потенциальной энергии, которой обладает жидкость в резервуаре, превращается с большими или меньшими потерями в кинетическую энергию свободной струи или капель. В зависимости от размеров и формы различают малые и большие отверстия в тонкой и толстой стенках (рис. 1.19).
Малым отверстием
называется такое отверстие, у которого поперечный размер а менее 0,1Н (где Н - действующий напор при круглом отверстии а = d). Большим отверстием называется такое отверстие, у которого поперечный размер а более 0,1Н
В зависимости от расположения отверстия и условий протекания жидкости различают совершенное и несовершенное, полное и неполное сжатие струи, истечение из затопленного (рис. 1.19, а) и незатопленного отверстия при постоянном и переменном напоре. Степень сжатия оценивается коэффициентом сжатия s, равным отношению площади поперечного сечения струи в месте сжатия (сос) к площади отверстия
14. Гидравлическое сопротивление трубопроводов и аппаратов. Расчет потерь давления на местные сопротивления.
«гидравлические сопротивления» понимают силы трения, возникающие в реальной жидкости при ее движении. На преодоление гидравлических сопротивлений поток жидкости расходует часть удельной энергии, которую называют гидравлическими потерями напора. Гидравлические потери зависят от режима движения жидкости, формы сечения русла и его изменения, характера поверхности стенок и вязкости жидкости. Гидравлические потери напора делятся на потери на трение по длине и местные потери. Потери напора по длине обусловлены силами внутреннего трения и представляют собой потери энергии. Они складываются из сопротивления трения о стенки и возрастают пропорционально длине трубы. Местные сопротивления возникают при изменении направления и скорости потока.
Потерю напора на трение при установившемся равномерном прямолинейном движении потока по трубопроводу круглого сечения можно найти по формуле Вейсбаха—Дарси:
или в единицах давления
где X — коэффициент гидравлического трения (коэффициент Дарси), зависящий от режима движения потока и шероховатости стенок трубопровода.
Для ламинарного режима X зависит только от числа Рейнольдса и определяется по формуле
Формула Вейсбаха—Дарси справедлива и для турбулентного режима. Но в этом случае коэффициент
X зависит не только от числа Re, но и от шероховатости труб.
Потери давления на местном сопротивлении определяется формулой:
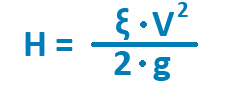по факту то же самое что и формулы выше
где H - потери на местном сопротивлении, м
ξ - коэффициент местного сопротивления,
V - скорость потока, м/с
g - ускорение свободного падения = 9.8 м/c2 .
Любое препятствие (сужения, повороты, запорная арматура и пр.) на пути движения потока жидкости вызывает вихреобразования и приводят к потерям давления в этом месте (отсюда и название "местные сопротивления"). Чем сильнее деформируется поток, тем больше будут потери давления.
Одни препятствия оказывают большее воздействие на поток, другие меньшее, величина влияния препятствия на поток характеризуется коэффициентом местного сопротивления ξ. Чем он выше тем больше сопротивление и тем больше будет потерь давления на нем.
15. Сопротивления трения. Расчет коэффициентов гидравлического трения. Влияние режимов течения и шероховатости на гидравлическое трение.
сила, обусловленная вязкостью жидкости (газа). Возникает в пограничном слое, где происходит изменение скоростей движения частиц от нуля до скорости набегающего потока. Преодоление сил сцепления между частицами жидкости (газа) создает суммарное усилие, направленное в сторону, противоположную движению. Зависит от величины обтекаемой поверхности, степени ее шероховатости, скорости движения тела и вязкости среды, в которой происходит движение.
Для определения коэффициента гидравлического трения необходимы данные:
Для ламинарного течения многочисленные экспериментальные исследования подтвердили справедливость вывода о том, что потери напора на гидравлические сопротивления зависят только от величины скорости движения потока в первой степени. Соответственно, гидравлический коэффициент трения
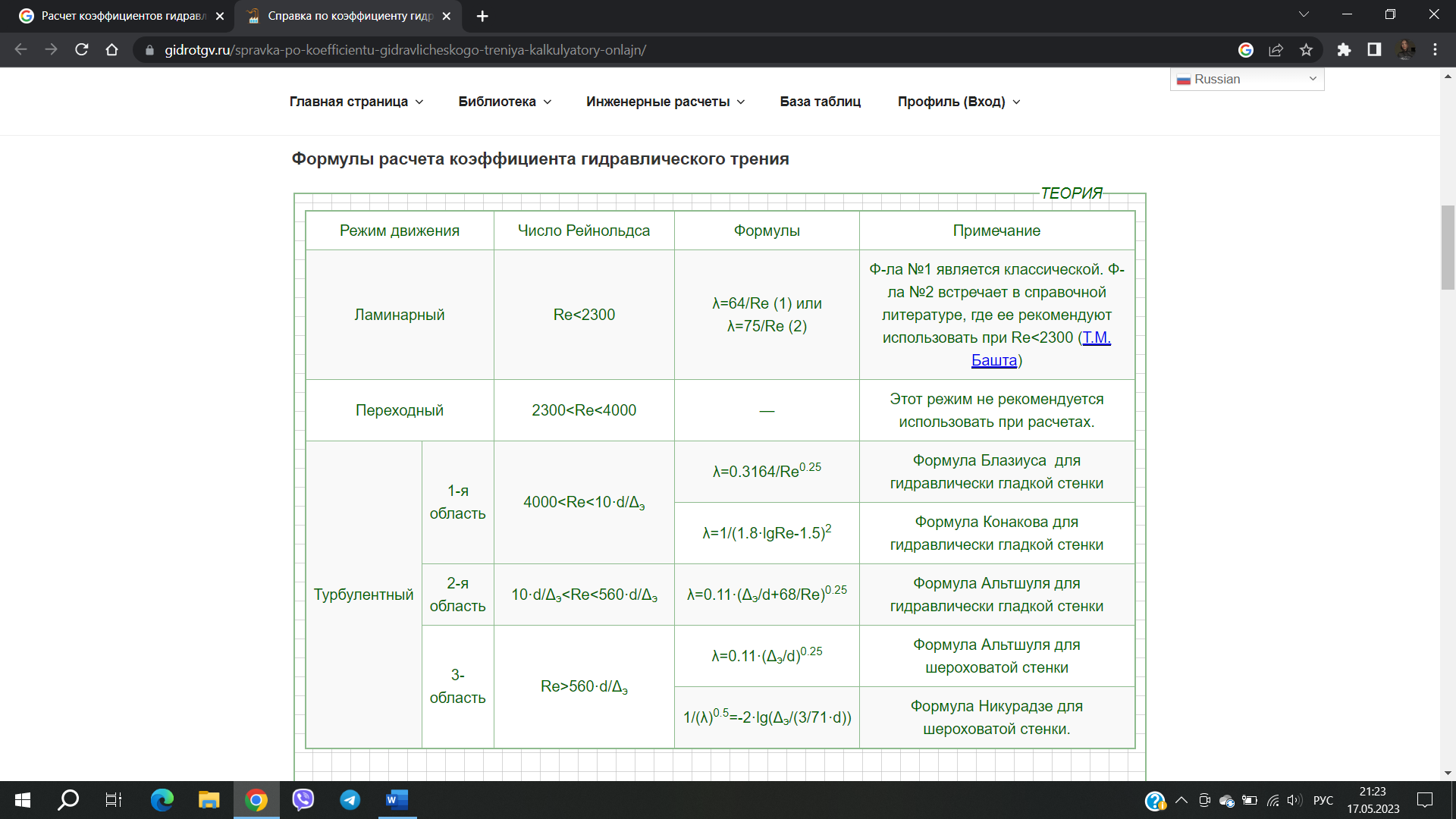
Опыты, прежде всего Г.А. Мурина с техническими трубопроводами, показали, что для турбулентного режима λ изменяется не только с изменением числа Re, но на величину λ влияет также техническое состояние трубы. Мурин исследовал 49 труб из различных материалов,бывших в эксплуатации, с различными диаметрами, при различных скоростях движения жидкости. Результаты опытов были получены в виде нескольких кривых (см. рис. 4.11).
Здесь четко различаются три области сопротивления при турбулентном режиме. Линия I соответствует области гидравлически гладких труб, когда величина λ зависит только от числа Re и не зависит от материала трубы. Математическая обработка данных показывает, что для этой области закономерна зависимость
Область II на графике является переходной областью от гидравлически гладких к шероховатым трубам. Величина λ зависит как от числа Re, так и от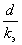
. Для определения λ в этой области лучше всего подходит формула Альтшуля
Эту формулу можно использовать в диапазоне чисел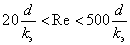
.
Область III является областью гидравлически шероховатых труб. На графике в этой области кривые зависимости λ от Reпараллельны между собой, т.е. λне зависит от числа Re, а определяется только величиной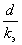 . В этой области λ определяется по формуле
которую можно использовать при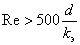
Гидродинамические трубки. Гидродинамические трубки предназначены для измерения местных скоростей в отдельных точках живого сечения потока жидкости.
Простейшей гидродинамической трубкой является трубка Пито. Трубка Пито изогнута под прямым углом и устанавливается в потоке навстречу течению жидкости. Если трубка установлена в открытом потоке, где на свободной поверхности жидкости давление равно атмосферному, то высота поднятия жидкости в трубке над поверхностью потока будет соответствовать скоростному напору.
Если жидкость движется в напорном трубопроводе, то для измерения скорости используется усовершенствованная трубка Пито—Прандтля. совершенствованная трубка Прандтля позволяет измерять скоростной и пьезометрический напоры. Прибор представляет собой хорошо обтекаемый цилиндр с концентрически расположенными в нем трубками. Приемником полного давления является отверстие осевого канала, а приемником пьезометрического напора — канавки на боковой поверхности цилиндра.
Помещая трубку Прандтля в различные точки поперечного сечения потока жидкости или воздуха, можно найти распределение скоростей в этом сечении и затем вычислить значение расхода. Трубку Прандтля можно также использовать в качестве датчика для измерения скорости полета самолета и других аппаратов.
Задача об истечении жидкости через отверстия - одна из основных в гидравлике и решается она уже две тысячи лет, восходя к Герону Александрийскому. Решение ее сводится к определению скорости истечения и расхода вытекающей жидкости. Этот случай движения характеризуется тем, что в процессе истечения запас потенциальной энергии, которой обладает жидкость в резервуаре, превращается с большими или меньшими потерями в кинетическую энергию свободной струи или капель. В зависимости от размеров и формы различают малые и большие отверстия в тонкой и толстой стенках (рис. 1.19).
Малым отверстием
называется такое отверстие, у которого поперечный размер а менее 0,1Н (где Н - действующий напор при круглом отверстии а = d). Большим отверстием называется такое отверстие, у которого поперечный размер а более 0,1Н
В зависимости от расположения отверстия и условий протекания жидкости различают совершенное и несовершенное, полное и неполное сжатие струи, истечение из затопленного (рис. 1.19, а) и незатопленного отверстия при постоянном и переменном напоре. Степень сжатия оценивается коэффициентом сжатия s, равным отношению площади поперечного сечения струи в месте сжатия (сос) к площади отверстия
14. Гидравлическое сопротивление трубопроводов и аппаратов. Расчет потерь давления на местные сопротивления.
«гидравлические сопротивления» понимают силы трения, возникающие в реальной жидкости при ее движении. На преодоление гидравлических сопротивлений поток жидкости расходует часть удельной энергии, которую называют гидравлическими потерями напора. Гидравлические потери зависят от режима движения жидкости, формы сечения русла и его изменения, характера поверхности стенок и вязкости жидкости. Гидравлические потери напора делятся на потери на трение по длине и местные потери. Потери напора по длине обусловлены силами внутреннего трения и представляют собой потери энергии. Они складываются из сопротивления трения о стенки и возрастают пропорционально длине трубы. Местные сопротивления возникают при изменении направления и скорости потока.
Потерю напора на трение при установившемся равномерном прямолинейном движении потока по трубопроводу круглого сечения можно найти по формуле Вейсбаха—Дарси:
или в единицах давления
где X — коэффициент гидравлического трения (коэффициент Дарси), зависящий от режима движения потока и шероховатости стенок трубопровода.
Для ламинарного режима X зависит только от числа Рейнольдса и определяется по формуле
Формула Вейсбаха—Дарси справедлива и для турбулентного режима. Но в этом случае коэффициент
X зависит не только от числа Re, но и от шероховатости труб.
Потери давления на местном сопротивлении определяется формулой:
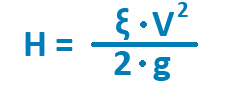по факту то же самое что и формулы вышегде H - потери на местном сопротивлении, м
ξ - коэффициент местного сопротивления,
V - скорость потока, м/с
g - ускорение свободного падения = 9.8 м/c2 .
Любое препятствие (сужения, повороты, запорная арматура и пр.) на пути движения потока жидкости вызывает вихреобразования и приводят к потерям давления в этом месте (отсюда и название "местные сопротивления"). Чем сильнее деформируется поток, тем больше будут потери давления.
Одни препятствия оказывают большее воздействие на поток, другие меньшее, величина влияния препятствия на поток характеризуется коэффициентом местного сопротивления ξ. Чем он выше тем больше сопротивление и тем больше будет потерь давления на нем.
15. Сопротивления трения. Расчет коэффициентов гидравлического трения. Влияние режимов течения и шероховатости на гидравлическое трение.
сила, обусловленная вязкостью жидкости (газа). Возникает в пограничном слое, где происходит изменение скоростей движения частиц от нуля до скорости набегающего потока. Преодоление сил сцепления между частицами жидкости (газа) создает суммарное усилие, направленное в сторону, противоположную движению. Зависит от величины обтекаемой поверхности, степени ее шероховатости, скорости движения тела и вязкости среды, в которой происходит движение.
Для определения коэффициента гидравлического трения необходимы данные:
-
-
о режиме движения среды. Определяется в ходе вычисления числа Рейнольдса —Re; -
о эквивалентной шероховатости стенки канала/трубы — Δэ. Зависит от материала из которого изготовлен канал/труба; -
о размерах сечения канала/трубы — d (характеризуется гидравлическим диаметром). Размеры сечения для систем задаются в ходе гидравлического или аэродинамического расчета.
-
Для ламинарного течения многочисленные экспериментальные исследования подтвердили справедливость вывода о том, что потери напора на гидравлические сопротивления зависят только от величины скорости движения потока в первой степени. Соответственно, гидравлический коэффициент трения
| |  . | (4.9) |
Опыты, прежде всего Г.А. Мурина с техническими трубопроводами, показали, что для турбулентного режима λ изменяется не только с изменением числа Re, но на величину λ влияет также техническое состояние трубы. Мурин исследовал 49 труб из различных материалов,бывших в эксплуатации, с различными диаметрами, при различных скоростях движения жидкости. Результаты опытов были получены в виде нескольких кривых (см. рис. 4.11).
Здесь четко различаются три области сопротивления при турбулентном режиме. Линия I соответствует области гидравлически гладких труб, когда величина λ зависит только от числа Re и не зависит от материала трубы. Математическая обработка данных показывает, что для этой области закономерна зависимость
| |  . |
Область II на графике является переходной областью от гидравлически гладких к шероховатым трубам. Величина λ зависит как от числа Re, так и от
. Для определения λ в этой области лучше всего подходит формула Альтшуля| |  . | (4.11) |
Эту формулу можно использовать в диапазоне чисел
.Область III является областью гидравлически шероховатых труб. На графике в этой области кривые зависимости λ от Reпараллельны между собой, т.е. λне зависит от числа Re, а определяется только величиной
. В этой области λ определяется по формуле| |  , | (4.12) |
которую можно использовать при