Файл: Эконометрика Практическое занятие Оценивание вероятностных характеристик. Проверка статистических гипотез.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 85
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Эконометрика
Практическое занятие 1. Оценивание вероятностных характеристик. Проверка статистических гипотез.
В таблицах файла Практика 1.xls приводятся данные о 3-х характеристиках 100 объектов (предприятий, стран, индивидов).
В ходе первой части занятия (оценка характеристик) от студентов требуется:
1) Построить гистограмму и полигон распределения показателя X.
2) Рассчитать среднее значение, выборочную дисперсию и среднее квадратическое отклонение. Построить 95%-ные доверительные интервалы (считать, что X имеет нормальное распределение).
3) Рассчитать выборочные коэффициенты асимметрии и эксцесса.
4) Построить диаграмму рассеяния.
5) Рассчитать выборочный коэффициент корреляции Пирсона.
6) Рассчитать ранговый коэффициент корреляции Спирмена.
В ходе второй части занятия (проверка гипотез) от студентов требуется:
1) Для X рассчитать выборочное среднее и выборочное с.к.о. Проверить гипотезы о равенстве математических ожиданий числам µ1 и µ2 (выбираются произвольными, например, µ1 – ближайшее «круглое» число к выборочному среднему, а µ2=2*µ1).
2) Для X рассчитать выборочные коэффициенты асимметрии и эксцесса. Используя эти значения, проверить гипотезу о нормальном распределении (тест Харке-Бера).
3) Для качественного признака B рассчитать относительную частоту наблюдения признака и проверить гипотезу о равенстве вероятности числу 0,5.
4) Для X и Y рассчитать выборочный коэффициент корреляции Пирсона и проверить его значимость.
5) Для X и Y рассчитать ранговый коэффициент корреляции Спирмена и проверить его значимость.
В третьей части (знакомство с Gretl) от студентов требуется:
1) Построить гистограмму распределения показателя X.
2) Рассчитать среднее значения, среднее квадратическое отклонение, выборочные коэффициенты асимметрии и эксцесса.
3) Для X проверить гипотезу о нормальном распределении.
4) Построить 95%-ные доверительные интервалы (считать, что X имеет нормальное распределение) для математического ожидания и дисперсии.
5) Для X проверить гипотезы о равенстве математического ожидания числам µ1 и µ2.
6) Для качественного признака B рассчитать относительную частоту наблюдения признака и проверить гипотезу о равенстве вероятности числу 0,5.
7) Для X и Y рассчитать выборочный коэффициент корреляции Пирсона и проверить его значимость.
8) Для X и Y рассчитать ранговый коэффициент корреляции Спирмена и проверить его значимость.
Части 1 и 2 выполняются в MS Excel, часть 3 выполняется в Gretl. Студенты выполняют тот вариант, который соответствует первой букве их фамилии. Предлагается 5 вариантов практических работ.
| Первая буква фамилии | Номер варианта |
| А, Б, В, Г,Д | 1-й вариант |
| Е, Ё,Ж, З, И, К | 2-й вариант |
| Л,М,Н, О, П, Р | 3-й вариант |
| С, Т, У, Ф, Х, Ц | 4-й вариант |
| Ч, Ш, Щ, Э, Ю, Я | 5-й вариант |
I. Оценивание вероятностных характеристик
1. Гистограмма - это способ представления статистических данных в графическом виде - в виде столбчатой диаграммы. Высота каждого столбца соответствует частоте появления значений параметров в выбранном диапазоне, а количество столбцов - на число выбранных диапазонов.
Для построения гистограммы потребуется сгруппировать данные. Для определения количества интервалов рекомендуется использовать формулу Стёрджеса:
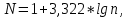
где n – объем выборки, для нахождения которого можно использовать функцию =СЧЁТ()
Впрочем, N может быть выбрано и произвольно.
Для нахождения минимального и максимального значений использовать функции =МИН() и =МАКС(). Ширину интервала определить:
L=(max-min)/N,
где N - рассчитанное или заданное Вами число интервалов.
Границы интервалов можно найти как:
min, min+L, min+2*L, ..., max.
Затем следует рассчитать частоты попадания показателя X (или Y) в каждый из интервалов. Для этого можно использовать функцию
=ЧАСТОТА(массив данных; массив интервалов)
Чтобы растянуть выражение, необходимо выделить диапазон ячеек, установить курсор в строку формул и нажать комбинацию Ctrl+Shift+Enter.
Для построения гистограммы: Вставка – Диаграммы – Гистограмма.
2. Выборочное среднее рассчитывается по формуле:
Чтобы не складывать вручную, можно использовать функцию =СУММ(). Впрочем, есть функция и для расчета среднего: =СРЗНАЧ().
Выборочная дисперсия рассчитывается по формуле:
Эта оценка является несмещенной. Редко в качестве оценки используют смещенную оценку:
Выборочное среднее квадратическое отклонение находят по формуле:
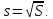
Вычисления можно оформить в виде таблицы:
| № |  |  |
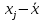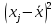| 1 |  |  |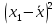
| … | … | … |
| n |  |  |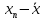
| | Сумма |  |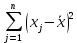
| Выборочная дисперсия |  | |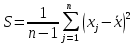
| Выборочное с.к.о. |  |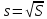
Для расчета можно использовать и стандартные функции =ДИСП() и =СТАНДОТКЛОН()
Полученные значения являются точечными оценками математического ожидания и дисперсии. Доверительный интервал (с надежностью 1-
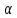) для математического ожидания нормально распределенной случайной величины:
,где
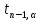- критическая точка распределения Стьюдента T(n-1) для уровня значимости 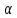(предполагается двусторонняя критическая область). Чтобы найти эту критическую точку
, можно воспользоваться функцией =СТЬЮДЕНТ.ОБР.2Х(α; n-1)
Доверительный интервал (надежность 1-
) для дисперсии нормально распределенной случайной величины:
.где
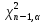- критическая точка распределения хи-квадрат χ2(n-1) для уровня значимости (критическая область правосторонняя). Чтобы найти эту критическую точку, можно воспользоваться функцией =ХИ2.ОБР.ПХ(α; n-1)3. Выборочный коэффициент асимметрии рассчитывается по формуле:
Вычисления можно оформить в виде таблицы:
| № |  |  |  |
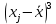| 1 |  |  |  |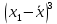
| … | … | … | … |
| n |  |  |  |
| | Сумма |  |  |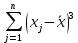
| Выборочный коэффициент асимметрии |  | ||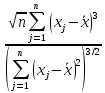
Для расчета можно использовать стандартную функцию =СКОС()
Примечание: в Excel используется формула с поправкой:
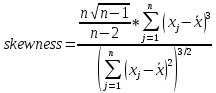
Выборочный коэффициент эксцесса
рассчитывается по формуле:
Вычисления можно оформить в виде таблицы:
| № | | |  |
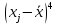| 1 | | |  |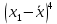
| … | … | … | … |
| n | | |  |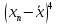
| | Сумма | |  |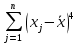
| Выборочный коэффициент эксцесса |  | ||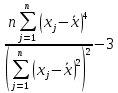
Для расчета можно использовать стандартную функцию =ЭКСЦЕСС()
Примечание: в Excel используется формула с поправкой:
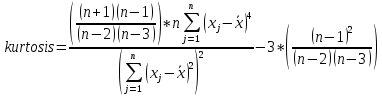
4. Диаграмма рассеяния предназначена для выявления зависимости между двумя показателями. С помощью этой диаграммы можно визуально определить корреляцию между двумя показателями.
Для построения гистограммы: Вставка – Диаграммы – Точечная.
Более детальный анализ предполагает получение оценки коэффициента корреляции.
| Истинный коэффициент корреляции R | Интерпретация |
| R=0 | Линейная связь между с.в. Xи Yотсутствует |
| R>0 | Связь прямая: большим значениям Xсоответствуют большие значения Y |
| R<0 | Связь обратная: меньшим значениям Xсоответствуют большие значения Y |