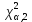(критическая область правосторонняя). Если JB_набл > 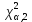, то нулевая гипотеза отвергается. Наблюдения противоречат тому, что распределение является нормальным.

4.2) Для наблюдаемого значения JB_набл определяется p-value. Если p-значение < α, нулевая гипотеза отвергается. Наблюдения противоречат тому, что распределение является нормальным.
Критическое значение 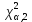(для правосторонней критической области) в Excel можно найти с помощью формулы:

= ХИ2.ОБР.ПХ(уровень значимости; 2)

Значение p-value (правосторонняя критическая область) можно определить с помощью формулы:

= ХИ2.РАСП.ПХ(JB_набл;2)
3. Проверка равенства вероятности некоторому значению δ:

1) Выбирается уровень значимости α.

2) Нулевая гипотеза 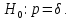Альтернативная гипотеза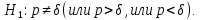

3) Рассчитывается наблюдаемое значение z-статистики:



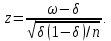
Если верна нулевая гипотеза, то z имеет стандартное нормальное распределение.

4.1) Наблюдаемое значение z_набл сравнивается с критическим значением. Если |z_набл| > z_α (или z_набл > z_α, или z_набл < z_α), то нулевая гипотеза отвергается (в первом случае критическая область двусторонняя, во 2-м – правосторонняя, в 3-м - левосторонняя). Наблюдения противоречат тому, что p=δ.

4.2) Для наблюдаемого значения z_набл определяется p-value (в первом случае критическая область двусторонняя, во 2-м – правосторонняя, в 3-м - левосторонняя). Если p-значение < α, нулевая гипотеза отвергается. Наблюдения противоречат тому, что p=δ.
Двусторонняя критическая область:

Критическое значение z_α в Excel можно найти с помощью формулы:

=НОРМ.СТ.ОБР(1-альфа/2)

Значение p-value можно определить с помощью формулы:

=2*НОРМ.СТ.РАСП(-ABS(z_набл); ИСТИНА)
Правосторонняя критическая область:

Критическое значение z_α в Excel можно найти с помощью формулы:

=НОРМ.СТ.ОБР(1-альфа)

Значение p-value можно определить с помощью формулы:

=1-НОРМ.СТ.РАСП(z_набл; ИСТИНА)
Левосторонняя критическая область:

Критическое значение z_α в Excel можно найти с помощью формулы:

---

= - НОРМ.СТ.ОБР(1-альфа)

Значение p-value можно определить с помощью формулы:

=НОРМ.СТ.РАСП(z_набл; ИСТИНА)
4. Проверка значимости коэффициента корреляции Пирсона.

Оценкой коэффициента корреляции является:



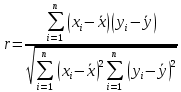
Одной лишь точечной оценки недостаточно для того, чтобы делать выводы. Необходимо проверить статистическую значимость коэффициента корреляции.
Пояснение: рассчитывая r, мы пытаемся получить оценку истинного коэффициента корреляции R с.в. X и Y. Поскольку r рассчитывается по ограниченной выборке, его значение отличается от R, значение которого интересует исследователя. Вполне возможна ситуация, когда корреляционной связи между X и Y на самом деле нет и R=0, а оценка r отличается от нуля.

Проверка значимости:

1) Выбирается уровень значимости α.

2) Нулевая гипотеза 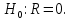Альтернативная гипотеза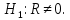

3) Рассчитывается наблюдаемое значение t-статистики:



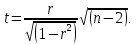
Если верна нулевая гипотеза, то t имеет распределение Стьюдента T(n-2) (аргумент в скобках называется "числом степеней свободы").

4.1) Наблюдаемое значение t_набл сравнивается с критическим значением t_α,n-2 (критическая область двусторонняя). Если |t_набл| > t_α,n-2, то нулевая гипотеза отвергается. В этом случае делается вывод о значимости коэффициента корреляции Пирсона, следовательно, существует зависимость между X и Y.

4.2) Для наблюдаемого значения t_набл определяется p-value (критическая область двусторонняя). Если p-значение < α, нулевая гипотеза отклоняется и делается вывод о значимости коэффициента корреляции.
Критическое значение t_α,n-2 (для двусторонней критической области) в Excel можно найти с помощью формулы:

= СТЬЮДЕНТ.ОБР.2Х(уровень значимости; размер выборки - 2)

Значение p-value можно определить с помощью формулы:

=СТЬЮДЕНТ.РАСП.2Х(|t_набл| ; размер выборки - 2)
5. Проверка значимости рангового коэффициента корреляции Спирмена.

Коэффициент ранговой корреляции Спирмена определяется формулой:



Проверка значимости

---

:

1) Выбирается уровень значимости α.

2) Нулевая гипотеза Альтернативная гипотеза

3) Рассчитывается значение t-статистики:



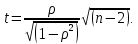
Если верна нулевая гипотеза, то t имеет распределение Стьюдента T(n-2) (аргумент в скобках называется "числом степеней свободы").

4.1) Наблюдаемое значение t_набл сравнивается с критическим значением t_α,n-2 (критическая область двусторонняя). Если |t_набл| > t_α,n-2, то нулевая гипотеза отвергается. В этом случае делается вывод о значимости коэффициента корреляции Пирсона, следовательно, существует зависимость между X и Y.

4.2) Для наблюдаемого значения t_набл определяется p-value (критическая область двусторонняя). Если p-значение < α, нулевая гипотеза отклоняется и делается вывод о значимости коэффициента корреляции.
Критическое значение t_α,n-2 (для двусторонней критической области) в Excel можно найти с помощью формулы:

= СТЬЮДЕНТ.ОБР.2Х(уровень значимости; размер выборки - 2)

Значение p-value можно определить с помощью формулы:

=СТЬЮДЕНТ.РАСП.2Х(|t_набл| ; размер выборки - 2)

III. Знакомство с Gretl

При проведении эконометрических исследований требуется строить большое количество моделей и проводить специальные тесты. Выполнять статистические исследования с помощью MS Excel не слишком удобно, поэтому вместо него лучше использовать профессиональные статистические/эконометрические пакеты (EViews, SPSS, Stata, STATISTICA и т.д.). В рамках нашего курса мы будем использовать Gretl - Gnu Regression, Econometrics and Time-series Library (в т.ч. и потому, что этот программный продукт является некоммерческим).
Скачать с официального сайта: http://gretl.sourceforge.net


После установки и запуска нужно импортировать данные из файла Практика 1.xls
ВАЖНО: используется исходный файл безо всяких расчетов. Желательно предварительно удалить лишние листы, оставив только свой вариант.


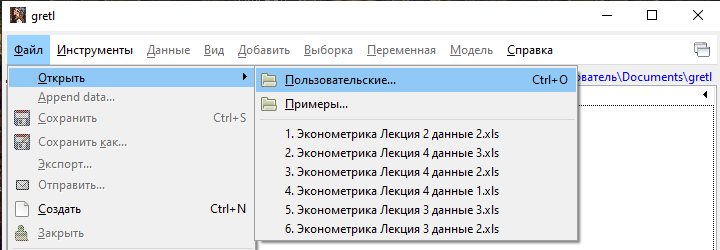
Выбирается расположение файла и формат (Файлы Excel *.xls)

---

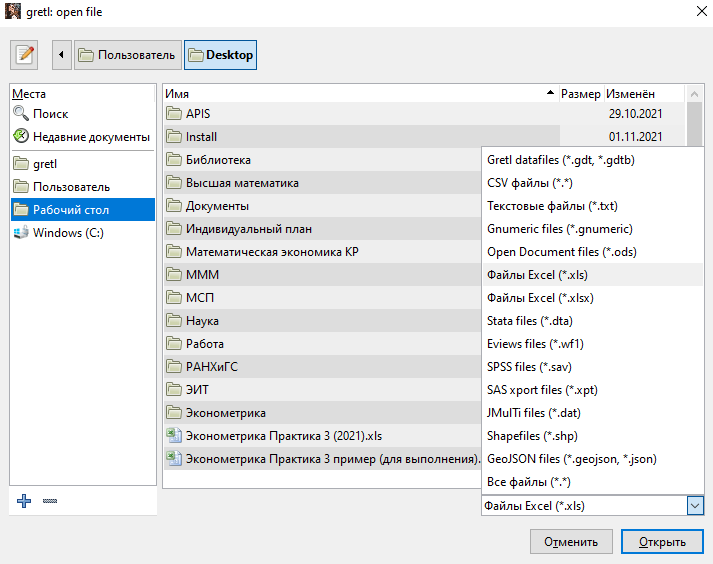
Поскольку в нашем примере обычные перекрестные данные, интерпретировать как временной ряд или панельные данные не нужно.

1. Гистограмма.

Для построения гистограммы следует выбрать переменную, после чего: Переменная – Распределение частот.



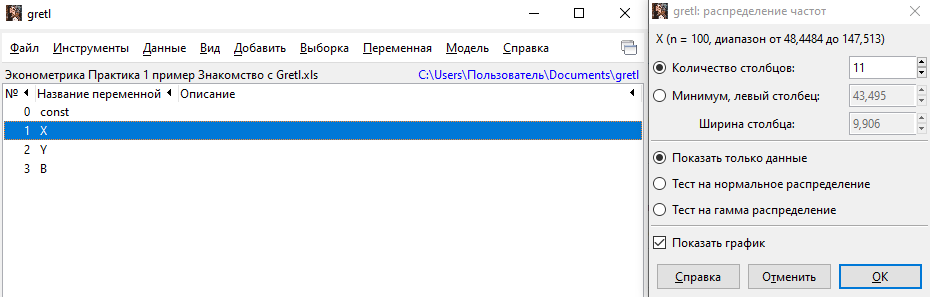
Получаем:


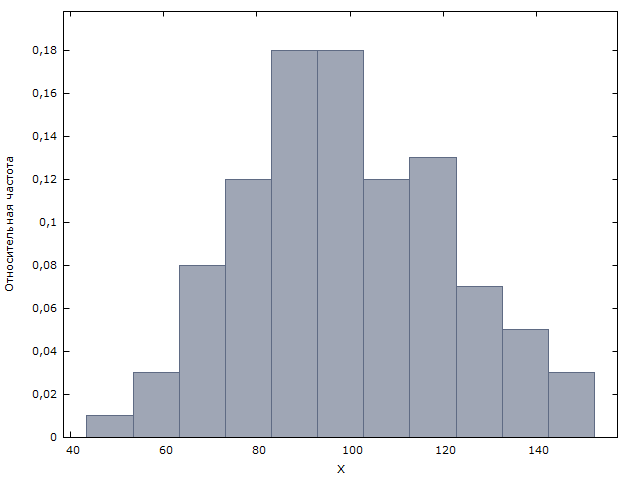
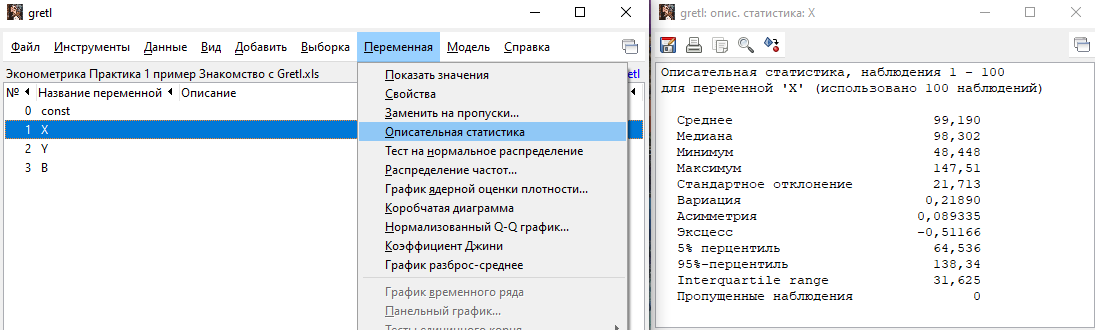
2. Описательная статистика.

Для расчета точечных оценок следует выбрать переменную, а затем: Переменная – Описательная статистика:


3. Проверка гипотезы о нормальном распределении.

В Gretl можно провести несколько тестов на нормальное распределение, в том числе тест Харке-Бера. Для этого следует выбрать переменную, а затем: Переменная – Тест на нормальное распределение:


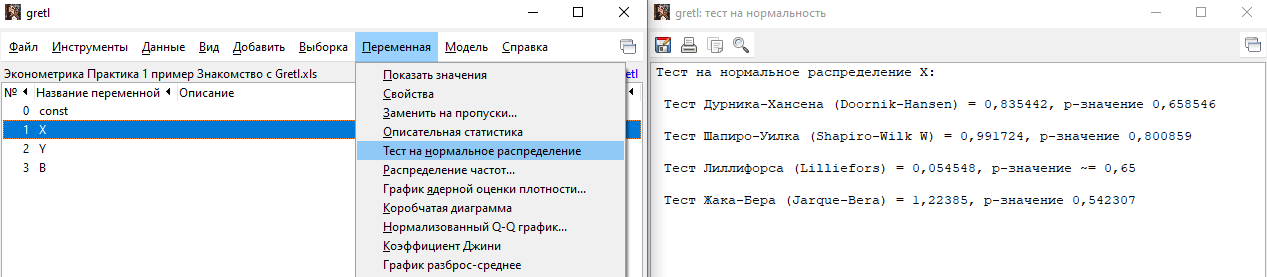
Каждый тест проводится по схеме:

1) Выбирается уровень значимости α.

2) Нулевая гипотеза H₀: распределение нормальное.

Альтернативная гипотеза H₁: распределение отличается от нормального.

3) Рассчитывается наблюдаемое значение тестовой статистики: для каждого теста свое.

4) Для наблюдаемого значения тестовой статистики определяется p-value. Если p-значение < α, нулевая гипотеза отвергается. Наблюдения противоречат тому, что распределение является нормальным.
В нашем примере для любого теста:









Нулевая гипотеза не отвергается во всех случаях.
4. Доверительные интервалы для математического ожидания и дисперсии.

Доверительный интервал (с надежностью 1- ) для математического ожидания нормально распределенной случайной величины:
,
где

---

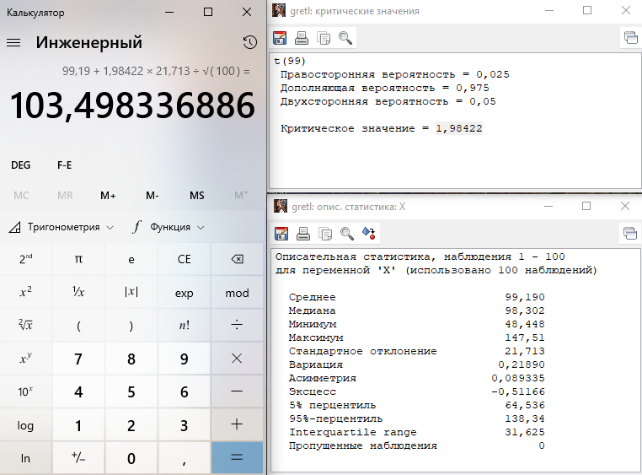
- критическая точка распределения Стьюдента T(n-1) для уровня значимости (предполагается двусторонняя критическая область). Чтобы найти эту точку: Инструменты - Критические значения – Стьюдента.



Правосторонняя вероятность = α/2, тогда двухсторонняя равна α
Получив критическое значение, используем его для расчета (можно воспользоваться встроенным калькулятором или провести вычисления в Excel):

Доверительный интервал (надежность 1- ) для дисперсии нормально распределенной случайной величины:

.

где - критическая точка распределения хи-квадрат χ²(n-1) для уровня значимости (критическая область правосторонняя), которая находится аналогично: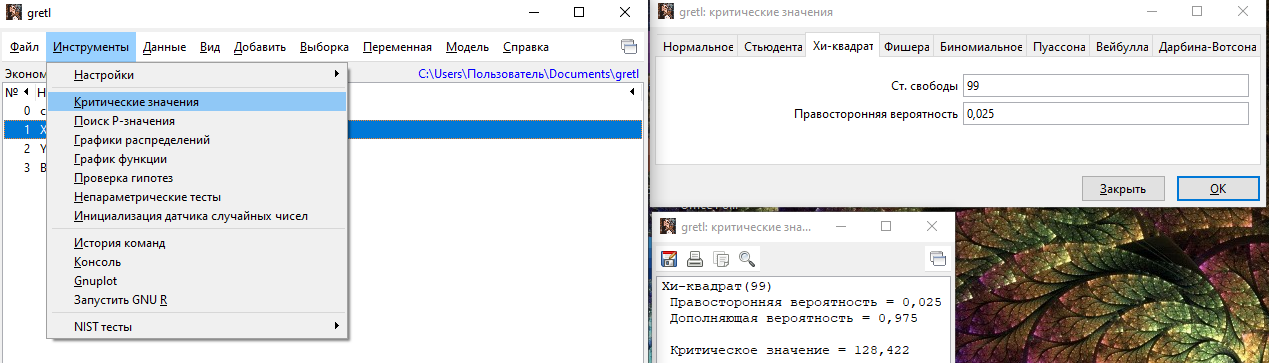



5. Проверка равенства математического ожидания нормально распределенной случайной величины некоторому значению µ.
В Gretl удобно проверять статистические гипотезы. Для этого: Инструменты – Проверка гипотез – Среднее.



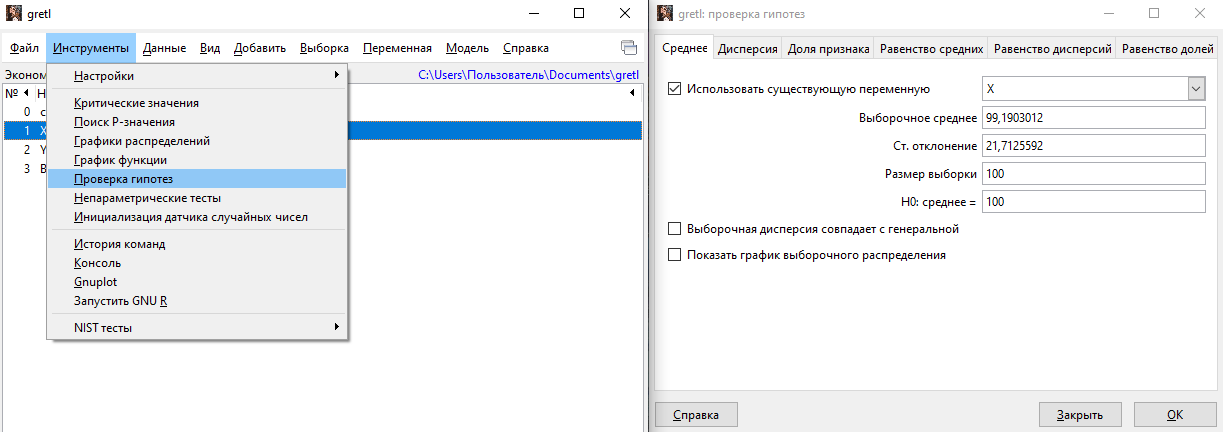
Если использовать существующую переменную, то заполнить нужно только поле «H0: среднее=», где и следует указать μ:











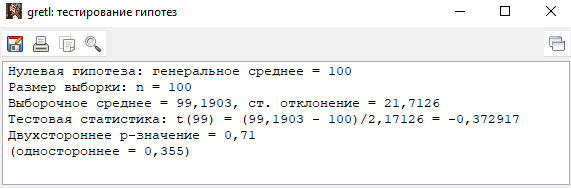
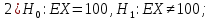
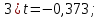
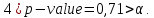
(при такой H₁ используется двухстороннее p-value)

Вывод: H₀ не отвергается. Данные не противоречат тому, что E(X)=100.
Проверим теперь 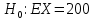против другой альтернативной гипотезы:

---

Смотрите также файлы

• Отчет по производственной практике научноисследовательская работа.docx

• 24. 10. 22 Понедельник 25. 10. 22 Вторник 26. 10. 22 Среда.docx

• Об одной задаче сопряжения для уравнения составного и гиперболического типов четвертого порядка.docx

• 3. Наиболее благоприятным диапазоном значений относительной влажности воздуха для человека является .doc

• Физиологические свойства миокарда и процессов, детерминированных этими свойствами.docx