5.Выборочный коэффициент корреляции Пирсона рассчитывается по формуле:



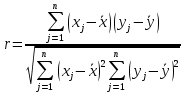
Вычисления можно оформить в виде таблицы:

№
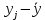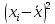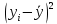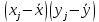1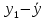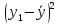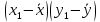
…	…		…		…		…
n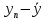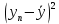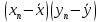
		Сумма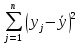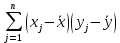
		Выборочный коэффициент корреляции Пирсона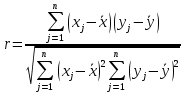

---

Для расчета в Excel используется функция:

=КОРРЕЛ(массив значений X; массив значений Y)
6. Ранговый коэффициент корреляции Спирмена.

Рассмотренный ранее коэффициент корреляции Пирсона неустойчив к выбросам (одна-единственная ошибка в данных может изменить вывод о характере связи). Также он не годится в том случае, если зависимость между X и Y является монотонной, но нелинейной. От этих недостатков свободен коэффициент корреляции Спирмена.
Расположим n пар наблюдений (x_i, y_i) по убыванию (или по возрастанию) x_i. Тогда первой будет пара с наибольшим значением фактора х, а n-й – с наименьшим. Припишем паре, стоящей на j-м месте число R(x_j) = j, называемое рангом по X. В том случае, когда для j-го, j+1-го, …, j+k-го мест значение x одинаково, ранг соответствующих пар полагается равным:



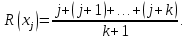
Аналогичным образом определяется R(y_j) - ранг поY.

Коэффициент ранговой корреляции Спирмена определяется формулой:



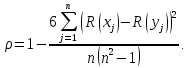
По своей сути это обычный коэффициент корреляции Пирсона, но рассчитанный не по значениям x_jи y_j, а по их рангам.

№	x	y	R(x)	R(y)	R(x)-R(y)	(R(x)-R(y))2
1	x1	y1	R(x1)	R(y1)	R(x1)-R(y1)	(R(x1)-R(y1))2
…	…	…	…	…	…	…
n	xn	yn	R(xn)	R(yn)	R(xn)-R(yn)	(R(xn)-R(yn))2
					Сумма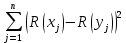
					Ранговый коэффициент корреляции Спирмена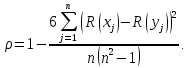

---

Для нахождения рангов в Excel используется функция

=РАНГ(значение X; массив значений X)

После нахождения рангов по X и по Yможно рассчитать коэффициент корреляции Спирмена с помощью функции:

=КОРРЕЛ(массив рангов по X; массив рангов по Y)
Все проделанные вычисления можно выполнить автоматически, используя пакет анализа MS Excel. Предварительно потребуется установить надстройку "Анализ данных".
Инструкция установке:

https://support.office.com/ru-ru/article/Загрузка-пакета-анализа-в-excel-6a63e598-cd6d-42e3-9317-6b40ba1a66b4
II. Проверка статистических гипотез
Статистическая гипотеза - это утверждение относительно значений параметров распределения элементов генеральной совокупности (параметров распределения случайной величины), из которой мы сделали случайную выборку.
Гипотеза, которую мы первоначально считаем истинной и проверяем, называется нулевой и обозначается H₀. Гипотеза, в пользу которой мы можем отвергнуть нулевую, называется альтернативной и обозначается H₁.
Правило, по которому решают, отвергнуть нулевую гипотезу в пользу альтернативной или не отвергнуть, называют статистическим критерием.
Возможные решения:

Решение \ Действительность	Верна H0	Верна H1
Принять H0	Правильное решение	Ошибка 2-го рода
Принять H1	Ошибка 1-го рода	Правильное решение

Вероятность ошибки первого рода (отвергнуть нулевую гипотезу тогда, когда она является истинной), называется уровнем значимости и обозначается α.
Критерии, как правило, основаны на некоторой тестовой статистике T - функции случайной выборки. Тестовая статистика строится таким образом, чтобы ее распределение в том случае, когда верна нулевая гипотеза, было известным.
Все пространство значений, которые может принимать с.в. T, делится на две взаимодополняющие области – область принятия нулевой гипотезы и область отклонения основной гипотезы (т.н. критическая область). Эти области зависят от уровня значимости α. Значение Т_α, разделяющее область принятия H₀ и критическую область, называется критическим значением.
Критические области обычно односторонние (правосторонние или левосторонние) или двусторонние (в частности, симметричные относительно 0).

---

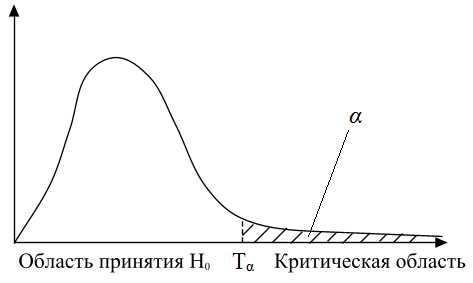
Правосторонняя критическая область
Если верна нулевая гипотеза, то вероятность того, что с.в. T попадет в критическую область, равна α. Как правило, в качестве α выбирают какое-либо маленькое число (обычно это 0,1, 0,05 или 0,01).
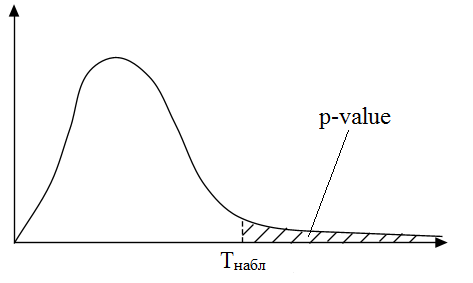
По выборке рассчитывается наблюдаемое значение тестовой статистики T_набл. Если оно попадает в критическую область, то H₀ отвергают в пользу H₁. Если T_набл попадает в область принятия, то H₀ не отвергают.
Наблюдаемый уровень значимости (p-value) – это такой уровень значимости, при котором T_набл оказывается на границе критической области и области принятия H₀. Если p-value<α, то H₀ отвергают в пользу H₁. Если же p-value>α, то H₀ не отвергают.


Проверка некоторых статистических гипотез

1. Проверка равенства математического ожидания нормально распределенной случайной величины некоторому значению µ:
1) Выбирается уровень значимости α.

2) Нулевая гипотеза 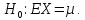Альтернативная гипотеза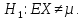

3) Рассчитывается наблюдаемое значение t-статистики:



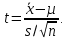
Если верна нулевая гипотеза, то t имеет распределение Стьюдента T(n-1) (аргумент в скобках называется "числом степеней свободы").

4.1) Наблюдаемое значение t_набл сравнивается с критическим значением t_α,n-1 (критическая область двусторонняя). Если |t_набл| > t_α,n-1, то нулевая гипотеза отвергается. Наблюдения противоречат тому, что EX=µ.

4.2) Для наблюдаемого значения t_набл определяется p-value (критическая область двусторонняя). Если p-значение < α, нулевая гипотеза отвергается. Наблюдения противоречат тому, что EX=µ.
Критическое значение t_α,n-1 (для двусторонней критической области) в Excel можно найти с помощью формулы:

= СТЬЮДЕНТ.ОБР.2Х(уровень значимости; размер выборки - 1)

Значение p-value можно определить с помощью формулы:

=СТЬЮДЕНТ.РАСП.2Х(|t_набл| ; размер выборки - 1)

---

Вариант этого теста с другой альтернативной гипотезой:

1) Выбирается уровень значимости α.

2) Нулевая гипотеза Альтернативная гипотеза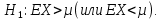

3) Рассчитывается наблюдаемое значение t-статистики:



Если верна нулевая гипотеза, то t имеет распределение Стьюдента T(n-1) (аргумент в скобках называется "числом степеней свободы").

4.1) Наблюдаемое значение t_набл сравнивается с критическим значением t_α,n-1 (критическая область правосторонняя в случае (>) и левосторонняя в случае (<)). Если t_набл > t_α,n-1 (или t_набл < t_α,n-1), то нулевая гипотеза отвергается. Наблюдения противоречат тому, что EX=a.

4.2) Для наблюдаемого значения t_набл определяется p-value (критическая область правосторонняя в случае (>) и левосторонняя в случае (<)). Если p-значение < α, нулевая гипотеза отвергается. Наблюдения противоречат тому, что EX=µ.
Критическое значение t_α,n-1 (для правосторонней критической области) в Excel можно найти с помощью формулы:

= СТЬЮДЕНТ.ОБР(1 - уровень значимости; размер выборки - 1)
Критическое значение t_α,n-1 (для левосторонней критической области) в Excel можно найти с помощью формулы:

= СТЬЮДЕНТ.ОБР(уровень значимости; размер выборки - 1)
Значение p-value (правосторонняя критическая область) можно определить с помощью формулы:

=1-СТЬЮДЕНТ.РАСП(t_набл; размер выборки - 1; ИСТИНА)
Значение p-value (левосторонняя критическая область) можно определить с помощью формулы:

=СТЬЮДЕНТ.РАСП(t_набл; размер выборки - 1; ИСТИНА)
2. Тест Харке-Бера (Jarque-Bera test). С помощью теста проверяется гипотеза о нормальности распределения:

1) Выбирается уровень значимости α.

2) Нулевая гипотеза H₀: распределение нормальное (SKEW=0, KURT=0).

Альтернативная гипотеза H₁: распределение отличается от нормального (SKEW≠0, KURT≠0).

3) Рассчитывается наблюдаемое значение статистики JB:



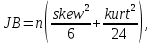
где skew и kurt – выборочные коэффициенты асимметрии и эксцесса.

Если верна нулевая гипотеза, то JB имеет распределение хи-квадрат χ²(2).

4.1) Наблюдаемое значение JB_набл сравнивается с критическим значением

---

Смотрите также файлы

• Отчет по производственной практике научноисследовательская работа.docx

• 24. 10. 22 Понедельник 25. 10. 22 Вторник 26. 10. 22 Среда.docx

• Об одной задаче сопряжения для уравнения составного и гиперболического типов четвертого порядка.docx

• 3. Наиболее благоприятным диапазоном значений относительной влажности воздуха для человека является .doc

• Физиологические свойства миокарда и процессов, детерминированных этими свойствами.docx