Показателем надежности называется численное значение критерия.

1. 
   Критерии надежности невосстанавливаемых систем и элементов
   

Отказ технического объекта является событием случайным, а время до его наступления является случайной величиной. Поэтому надежность характеризуется комплексом некоторых статистических величин. Основной характеристикой надежности невосстанавливаемой системы и ее элементов является функция распределения продолжительности безотказной работы F(t) при t ≥ 0. На ее основании определяются все остальные критерии надежности, а именно:

P(t) - вероятность безотказной работы в течение времени t;

Q(t) - вероятность отказа в течение времени t;

f(t) - плотность распределения времени безотказной работы;

λ(t) - интенсивность отказа в момент времени t;

T₁ - среднее время безотказной работы (средняя наработка до отказа);

Λ(t) - функция ресурса;

t_γ – γ - процентный ресурс.

Вероятностью безотказной работы P(t) называется вероятность того, что объект не откажет в течение времени t. Величина P(t) является убывающей функцией времени и имеет свойства:

0 ≤ P(t) ≤ 1; P(0) = 1; P(∞) = 0.

В результате опытов и в ходе эксплуатации накапливаются статистические данные об отказах. По этим данным величина P(t) может быть определена, как:

P^*(t) = N(t) / N₀ = (N₀ - n(t)) / N₀,

где N₀ – общее число испытанных объектов; N(t) - число исправно работавших объектов в момент времени t; n(t) - число отказавших объектов в момент времени t.

Индексом «*» обозначаются величины, полученные по статистическим данным.

Вероятность безотказной работы является интервальной оценкой, т.к. характеризует надежность в интервале времени от 0 до t. Она достаточно просто определяется и хорошо характеризует надежность объекта. При помощи этой величины определяются многие важные показатели техники, такие, как эффективность, безопасность, живучесть и риск.

Вероятностью отказа Q(t) называется вероятность того, что объект обязательно откажет в течение времени t. Эта величина определяется как:

Q(t) = 1 - P(t).

Плотность распределения времени безотказной работы f(t) - это плотность распределения случайной величины времени до отказа.

---

Это точечная характеристика, наиболее полно характеризующая надежность объекта в данный текущий момент времени.

По статистическим данным величина f^*(t) определяется путем сравнения данных, полученных для работы объекта в течение времени t и времени t + Δt. При этом считается, что интервал Δt достаточно мал. Тогда:

f^*(t) = n(t, t + Δt) / (N₀·Δt) = (N(t) - N (t + Δt )) / (N₀·Δt) = (Р(t) - Р (t + Δt )) / Δt,

где n(t, t + Δt) – число отказавших объектов за промежуток времени от t до t + Δt; N₀ – общее число испытанных объектов; N(t) - число исправно работавших объектов к моменту времени t; N (t + Δt ) - число исправно работавших объектов к моменту времени t + Δt; Р(t) - вероятность безотказной работы в течение времени t; Р(t + Δt) - вероятность безотказной работы в течение времени t + Δt.

Величина f(t) показывает, как часто случаются отказы с течением времени.

Интенсивностью отказов λ(t) называется отношение плотности распределения времени безотказной работы f(t) к вероятности безотказной работы объекта Р(t):

λ(t) = f(t) / Р(t).

По статистическим данным величина λ^*(t) определяется, как:

λ^*(t) = n(t, t + Δt) / (N_ср·Δt),

где N_ср – среднее число исправно работавших объектов в интервале времени (t, t + Δt).

N_ср = (N(t) + N (t + Δt )) / 2.

В ряде случаев вероятность безотказной работы Р(t) через интенсивность отказов λ(t) может быть найдена из выражения:

Р(t) = е ^{- λ(t)·t}.

Для сложных технических систем, таких как контактная сеть, интенсивность отказов λ(t) является одним из основных критериев надежной работы. Это вызвано тем, что интенсивность отказов обладает хорошей наглядностью, достаточно просто определяется расчетным путем и позволяет легко определить другие величины, характеризующие надежность систем и их элементов.

Опыт эксплуатации объектов ЭСЖТ показывает, что в большинстве случаев имеют место три периода, характеризующиеся различным уровнем интенсивности отказов и разными закономерностями изменения интенсивности отказов во времени. Типичное распределение интенсивности отказов по времени эксплуатации объекта имеет вид, представленный на рисунке 1.

λ(t)



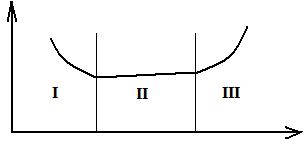
Рисунок 1 λ(t) - характеристика из трех типичных периодов:

I – приработка; II

---

– нормальная эксплуатация; III – старение

Первый период эксплуатации называется приработкой. В этот период интенсивность отказов высока, что объясняется недостаточным качеством поступающих в эксплуатацию изделий. Изделия со скрытыми дефектами, не выявленными в процессе производства, контроля и испытаний, теряют работоспособность в начале эксплуатации.

---

Второй период эксплуатации называется нормальной эксплуатацией. В этот период интенсивность отказов практически не зависит от наработки изделия. Изделия отказывают, как правило, внезапно из-за случайных причин, не учтенных при их проектировании (повышенные нештатные нагрузки, попадание посторонних предметов, нарушение правил эксплуатации и т.п.).

Третий период эксплуатации называется периодом старений. В этот период интенсивность отказов существенно возрастает. Причиной тому служит износ изделий и их составных частей, накопление в них незначительных повреждений, способных в сумме вызвать отказ.

Имея распределение интенсивности отказов, мы можем с достаточной степенью достоверности предугадать поведение объекта в эксплуатации и своевременно принять меры по предотвращению отказа. Например, путем своевременной замены, ремонта или регулировки.

Средним временем безотказной работы (средней наработкой до отказа) T₁ называется математическое ожидание времени безотказной работы объекта:

Т₁ = М(t).

По статистическим данным об отказах величина Т^* ₁ определяется , как:

Т^*₁ =( _i )/ n_от,

где t_i – время безотказной работы i-го объекта; n_от – число отказов объектов при работе всех испытанных объектов.

Между средним временем безотказной работы объекта Т₁ и вероятностью его безотказной работы существует зависимость вида:

Т₁ = dt.

Функция ресурса Λ(t) определяется, как:

Λ(t) = - ln = dt.

Упрощенно функция ресурса определяется как интенсивность отказов за время, умноженная на продолжительность этого времени:

Λ(t) = λ(t)· t.

γ - процентный ресурс t_γ – это наработка, в течении которой не происходит отказа с вероятностью γ /100, что выражается соотношением:

Р(t_γ) = γ /100.

1. 
   Критерии надежности восстанавливаемых систем и элементов
   

---

Надежность восстанавливаемых объектов оценивается при помощи тех же критериев. что и надежность восстанавливаемых объектов. Это объясняется тем, что в процессе работы восстанавливаемые объекты могут считаться невосстанавливаемыми, т.к. их ремонт во время работы в большинстве случаев невозможен. Однако для восстанавливаемых объектов используется целый ряд дополнительных критериев надежности, а именно:

Т – среднее время работы между отказами (средняя наработка на отказ);

Т_в – среднее время восстановления;

ω(t) – параметр потока отказов;

К_г(t) – функция готовности;

К_п(t) – функция простоя;

К_г – коэффициент готовности;

К_г – коэффициент простоя.

Среднее время работы между отказами Т (средняя наработка на отказ) – это отношение средней суммарной наработки к числу отказов при длительной работе. По статистическим данным величина Т^* определяется, как:

Т^* =( _i )/ n_от,

где t_i – время безотказной работы i-го объекта; n_от – число отказов объектов при работе всех испытанных объектов.

Среднее время восстановления Т_в – это отношение среднего суммарного времени восстановления объектов, к среднему числу восстановлений при длительной работе объектов.

По статистическим данным величина Т^* _в определяется, как:

Т^*_в =( _в )/ n_в,

где N_в – общее число восстановлений объектов; t_в– время восстановления работы i-го объекта; n_в – число восстановлений при работе всех испытанных объектов.

Параметром потока отказов ω(t) называется скорость изменения (первая производная) среднего числа отказов в момент времени t.

По статистическим данным величина ω*(t) определяется как отношение числа отказавших объектов в единицу времени к общему числу испытанных объектов N₀, при условии, что отказавшие объекты заменяются на исправные и вновь ставятся на испытание:

ω*(t) = n(t, t + Δt) / (N₀·Δt).

Функцией готовности К_г(t) называется вероятность того, что восстанавливаемая система исправна в момент времени t.

---

Смотрите также файлы

• Содержание Введение 3 Особенности применения упрощенной системы налогообложения 4 Цели и задачи аудита применения усно 8 Методика аудиторской проверки ведения операций в рамках усно 9 Заключение 12 Библиографический список 13 Введение.doc

• Классный час народов многодружба одна.doc

• О. Конт 3 леуметтану з алдына ылым ретінде мына асырда пайда болды 19асырда 4 Социология.docx

• Технология реабилитационной работы с людьми, страдающими алкоголизмом.rtf

• 1 Содержание стр.docx