ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВРЕМЕНИ ДО ОТКАЗА

Для практических расчетов показателей надежности системы электроснабжения и ее элементов используются различные законы распределения времени до отказа. Выбор того или иного закона осуществляется исходя из физической сущности наблюдаемых явлений. Рассмотрим наиболее часто применяемые законы.

1. 
   Экспоненциальный закон распределения
   

Экспоненциальное или показательное распределение времени до отказа характерно для работы многих объектов контактной сети на этапе нормальной работы, т.е. с момента окончания приработки до момента проявления постепенных отказов, вызванных старением.

Экспоненциальный закон распределения является однопараметрическим – имеет один параметр, при помощи которого можно описать изменение всех остальных интересующих нас величин. Этим параметром является интенсивность отказов λ. Для экспоненциального закона справедливо выражение λ = const, что означает постоянство величины интенсивности отказов на всем интервале рассматриваемого времени. Другие критерии надежности определяются при помощи выражений:

Р(t) = е ^{- λ·t}.

Q(t) = 1 - е ^{- λ·t}.

f(t) = λ·е ^{- λ·t}.

T₁ = 1/λ.

Λ(t) = λ·t.

t_γ = -(1/ λ)·(ln γ/100).

Пример: Время безотказной работы питающего зажима контактной сети подчинено экспоненциальному закону с параметром распределения λ = 0,000005 час^-1. Определить показатели надежности питающего зажима при его работе в течении 8760 часов (1 года).

P(t) = Р(t) = е ^{- λ·t} = 0,9571.

Q(t) = 1 - е ^{- λ·t} = 0,0429.

f(t) = λ·е ^{- λ·t} = 0,00000479 час^-1.

T₁ = 1/λ = 200000 час.

Λ(t) = λ·t = 0,0438

Для γ = 5 t_γ = -200000· ln 0,05 = 599146 час.

Для случая экспоненциального закона вероятность безотказной работы с ростом времени наработки убывает по экспоненте (рисунок 1).



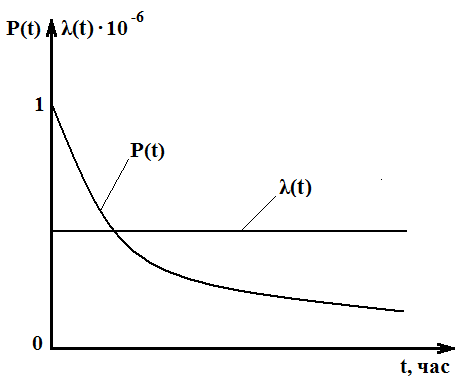
Рисунок 1. Характер изменения вероятности безотказной работы P(t) и интенсивности отказов λ(t) при экспоненциальном законе распределения времени до отказа

В ряде случаев необходимо вычислять математическое ожидание М(Х), дисперсию D(X) и среднее квадратическое отклонение σ(X). Для экспоненциального закона распределения эти величины определяются, как:

---

М(Х) = 1/λ; D(X) = 1/λ²; σ(X) = 1/λ.

2. 
   Нормальный закон распределения
   

Нормальное распределение времени до отказа или распределение Гаусса является наиболее общим законом распределения. Согласно теории больших чисел любое распределение всегда подчиняется нормальному закону в том случае, когда на объект оказывают влияние многие примерно однозначные факторы. Таким образом, нормальное распределение охватывает весь жизненный цикл объекта, а не только его отдельные этапы. Для рассмотренного выше экспоненциального закона распределения характерным являлся этап нормальной работы.

Нормальный закон распределения является двухпараметрическим – имеет два параметра, при помощи которых можно описать изменение всех остальных интересующих нас величин. Этими параметрами являются математическое ожидание m и среднее квадратическое отклонение σ времени безотказной работы элемента.

Математическая запись функции плотности вероятности безотказной работы при нормальном распределении имеет вид:

_{2 2}

f(t) = 1 / (σ· π)·е^{-(t – m ) / (2 σ )} , - ∞ ≤ t ≤ + ∞.

Этому выражению соответствует график плотности вероятности безотказной работы, представленный в виде y = f(t) на рисунке 2.

Для данного распределения вероятность безотказной работы определяется, как:

_{2 2}

P(t) = ^{-( t – m ) / (2 σ )}·dt = 0,5 – Ф₀((t – m)/σ),

где Ф₀ – функция Лапласа, значение которой определяется по таблицам.



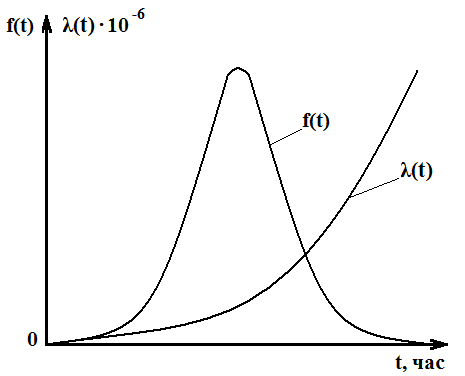
Рисунок 2. Характер изменения плотности вероятности безотказной работы f(t) и интенсивности отказов λ(t) при нормальном законе распределения времени до отказа

3. 
   Усеченный нормальный закон распределения
   

В случае, когда случайная величина изменяется в диапазоне 0 ≤ t ≤∞, применяется усеченное нормальное распределение. При этом функция плотности вероятности безотказной работы определяется, как:

_{2 2}

f(t) = с / (σ₀·

---

π)·е^{-(t – mо ) / (2 σо )} , 0 ≤ t ≤ + ∞.

Усеченное нормальное распределение также является двухпараметрическим и зависит от математического ожидания m₀ и среднего квадратического отклонения σ₀ времени безотказной работы элемента. Величина m₀ соответствует максимальному значению функции f(t) и называется модой.

Коэффициент с определяется из выражения:

с = 1 / (0,5 – Ф₀(m₀ /σ₀))

Между величинами m ,σ и m₀ , σ₀ существуют связи, вида:

_____________

m = m₀ + k·σ₀; σ₀ = σ₀·√(1+k·m_о/σ_о–k²) ,

_{2 2}

где k = (с / π)·е^{-( mо ) / (2 σо )} .

4. 
   Логарифмически нормальный закон распределения
   

Логарифмически нормальный закон распределения используется для описания случайных величин, представляющих собой произведение достаточно большого числа случайных величин.

Логарифмически нормальное распределение является двухпараметрическим и зависит от двух параметров μ и s.

Функция плотности вероятности безотказной работы определяется, как:

_{2 2}

f(t) = 1/ (st· π)·е^{-(lnt – μ) / (2 s )}.

Между величинами m ,σ и μ, s существуют связи, вида:

_{2 2 2}

m = е^{0,5(2 μ + s )}; σ = (е^{(2μ + s )} ·(е^s – 1))^0,5

5. 
   Закон распределения Вейбулла
   

Логарифмически нормальный закон распределения используется для описания процессов усталостных разрушений. Распределение Вейбулла является двухпараметрическим с параметром формы α и параметром масштаба β.

Функция плотности вероятности безотказной работы определяется, как:

_α

f(t) = α·t^{α - 1}· е^-(t / ^β) / β^α.

Математическое ожидание и среднее квадратическое отклонение определяются из выражений:

m = βГ(1 + 1/ α); σ = β(Г(1 + 2/ α) – Г²(1 + 1/ α))^0,5,

где Г = - гамма функция.

Распределение Вейбулла является универсальным, поскольку при определенных значениях параметра α оно превращается в другие распределения. При α = 1 распределение превращается в экспоненциальное; при α < 1функции плотности и интенсивности отказав убывающие; при α >1функция

---

интенсивности отказав возрастающая; при α = 2 функция интенсивности отказав линейная; при α = 3,3 распределение близко к нормальному распределению.

ЛИТЕРАТУРА:

1. 
   Надежность и диагностика систем электроснабжения железных дорог: Учебник для вузов ж/д транспорта/ А.В. Ефимов, А.Г. Галкин. – М.: УМК МПС России, 2000, 512 с.
   

ЛЕКЦИЯ №3

Время: 2 часа

ЦЕЛЬ ЗАНЯТИЯ: Рассмотреть надежность системы электроснабжения как сложной технической системы с большим числом состояний, познакомиться с разработкой моделей надежности функционирования системы электроснабжения и изучить методы обеспечения и повышения ее надежности.

УЧЕБНЫЕ ВОПРОСЫ:

ВВЕДЕНИЕ – 5 мин.

1. 
   АНАЛИЗ НАДЕЖНОСТИ СИСТЕМЫ ЭЛЕКТРОСНАБЖЕНИЯ КАК СЛОЖНОЙ ТЕХНИЧЕСКОЙ СИСТЕМЫ С БОЛЬШИМ ЧИСЛОМ СОСТОЯНИЙ – 20 мин.
   
2. 
   РАЗРАБОТКА МОДЕЛЕЙ НАДЕЖНОСТИ ФУНКЦИОНИРОВАНИЯ СИСТЕМЫ ЭЛЕКТРОСНАБЖЕНИЯ – 20 мин.
   
3. 
   МЕТОДЫ ОБЕСПЕЧЕНИЯ И ПОВЫШЕНИЯ НАДЕЖНОСТИ СИСТЕМЫ ЭЛЕКТРОСНАБЖЕНИЯ. ПРОБЛЕМЫ СОЗДАНИЯ ВЫСОКОНАДЕЖНЫХ СИСТЕМ. АБСОЛЮТНО НАДЕЖНЫЕ СИСТЕМЫ – 5 мин.
   

ЗАКЛЮЧЕНИЕ – 5 мин.

ЛИТЕРАТУРА

1. 
   АНАЛИЗ НАДЕЖНОСТИ СИСТЕМЫ ЭЛЕКТРОСНАБЖЕНИЯ КАК СЛОЖНОЙ ТЕХНИЧЕСКОЙ СИСТЕМЫ С БОЛЬШИМ ЧИСЛОМ СОСТОЯНИЙ
   

Система электроснабжения является сложной системой, включающей в себя большое количество различных элементов и устройств. Кроме этого, в процессе технической эксплуатации системы электроснабжения используется большое количество машин, приборов и механизмов. Существенную роль играют люди, участвующие в обеспечении жизненного цикла системы электроснабжения, начиная от ее проектирования до момента снятия с эксплуатации. В результате система электроснабжения, как сложная техническая система, с точки зрения надежности характеризуется следующими основными свойствами:

- большое количество функционально связанных между собой элементов;

- наличие естественной и искусственной избыточности;

- многофункциональность;

- восстанавливаемость;

- неоднозначность понятия «отказ»;

- неодновременность работы элементов.

В соответствии с этими свойствами, основными характеристиками такой системы, определяемыми ее надежностью, являются качество, эффективность, безопасность, живучесть, риск, готовность и долговечность.

---

Для обеспечения высокой надежности системы электроснабжения как сложной технической системы необходимо решить ряд задач, таких как:

- научное обоснование критериев и показателей надежности системы электроснабжения;

- разработка моделей обеспечения надежности функционирования системы электроснабжения и алгоритмов их практической реализации;

- разработка инженерных методов анализа надежности устройств системы электроснабжения на всех этапах их жизненного цикла;

- практическое обеспечение высокой надежности системы электроснабжения.

Как было отмечено выше для системы электроснабжения, как сложной многофункциональной системы, не существует единственного критерия, достаточно полно характеризующего ее надежность. Анализ необходимых свойств системы электроснабжения, таких как ее качество, эффективность, безопасность, живучесть, риск, готовность и долговечность позволяет выделить основные критерии, описывающие надежность как комплексное свойство.

Так, например, для достижения заданной эффективности системы необходимо гарантировать определенное значение вероятности безотказной работы, для обеспечения долговечности – среднее время безотказной работы, для обеспечения готовности – определенное значение коэффициента готовности.

Мы знаем, что все критерии надежности связаны между собой строгими математическими зависимостями, по этому, задавая требования на множество критериев необходимо эти зависимости учитывать. Если этого не делать, то между заданными характеристиками возникнут очевидные противоречия.

Пример. Время безотказной работы питающего зажима контактной сети подчинено экспоненциальному закону. Для обеспечения заданной эффективности работы зажима зададим на интервале времени 8760 часов (1 год) значение вероятности безотказной работы Р(t) = 0,9571, а для обеспечения долговечности питающего зажима зададим значение среднего времени безотказной работы Т₁ = 100000 часов.

Для экспоненциального закона вероятность безотказной работы Р(t) = е ^-λ·t. Подставляя заданные значения, получим равенство 0,9571= е ^-λ·100000. Находим величину интенсивности отказов λ = 5·10^-6 час. По этой величине определим среднее время безотказной работы T

---

Смотрите также файлы

• Содержание Введение 3 Особенности применения упрощенной системы налогообложения 4 Цели и задачи аудита применения усно 8 Методика аудиторской проверки ведения операций в рамках усно 9 Заключение 12 Библиографический список 13 Введение.doc

• Классный час народов многодружба одна.doc

• О. Конт 3 леуметтану з алдына ылым ретінде мына асырда пайда болды 19асырда 4 Социология.docx

• Технология реабилитационной работы с людьми, страдающими алкоголизмом.rtf

• 1 Содержание стр.docx