Файл: Расчет валов на статическую, усталостную прочность и жесткость Рекомендовано редакционноиздательским советом угату в качестве учебного пособия уфа 200 3.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 254
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 и 2 (рис. 5.4, а, б). Построим эпюры изгибающих моментов 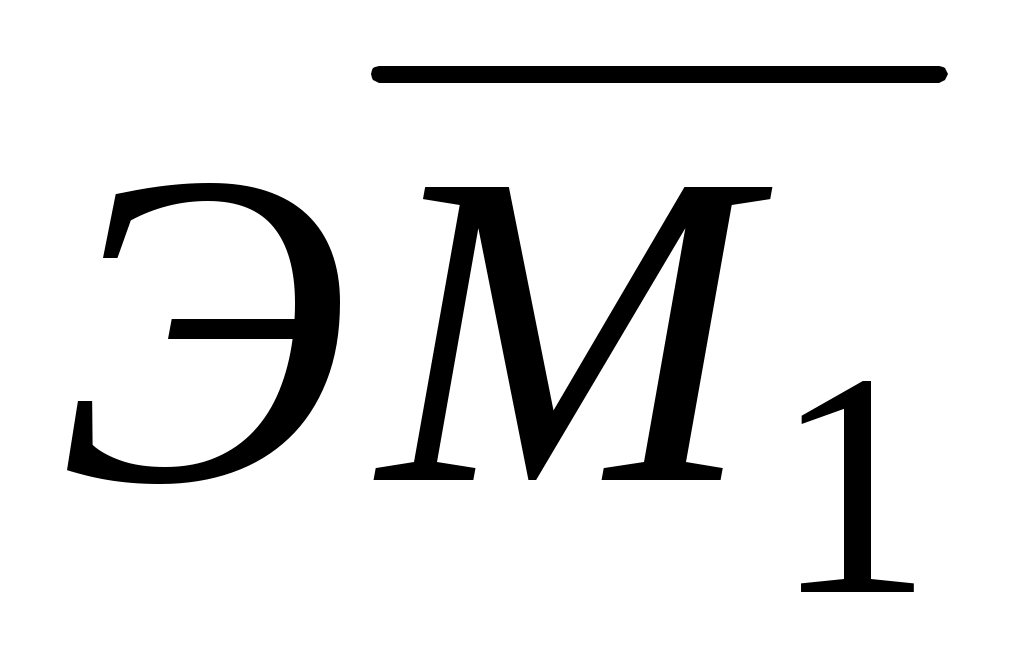 и
и 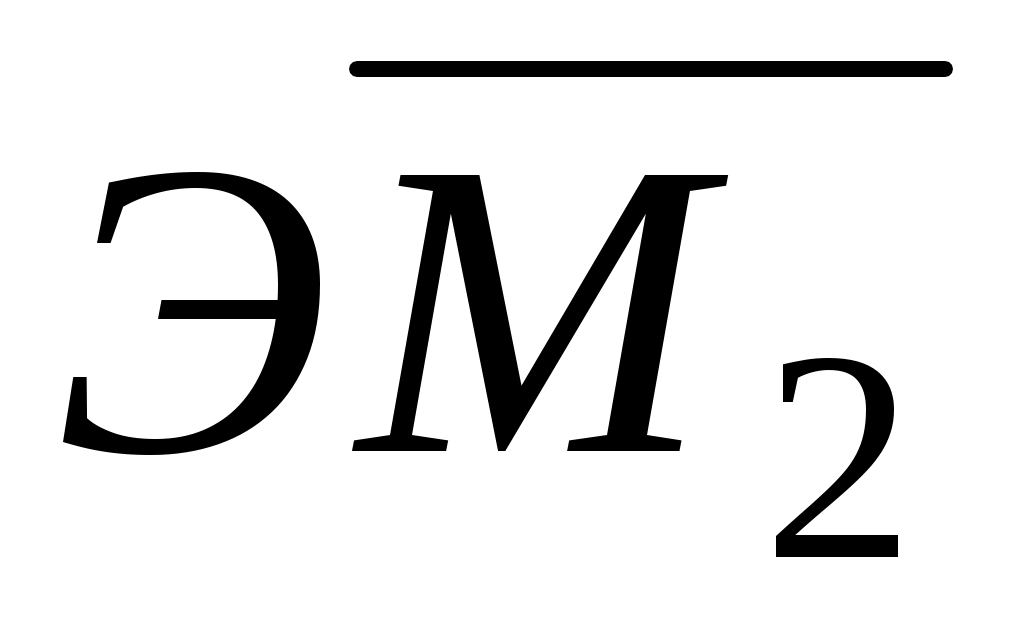 для этих состояний (рис. 5.4, в, г).
для этих состояний (рис. 5.4, в, г).
Разобьем эпюру изгибающих моментов ЭМz на элементарные фигуры, площади которых обозначим 1, 2, 3, 4 (рис. 5.4, д). Определим положения центров тяжести с1, с2, с3, с4 фигур. Вычислим значения площадей iи ординат ji, взятых под с1, с2, с3, с4 на эпюрах
ji, взятых под с1, с2, с3, с4 на эпюрах 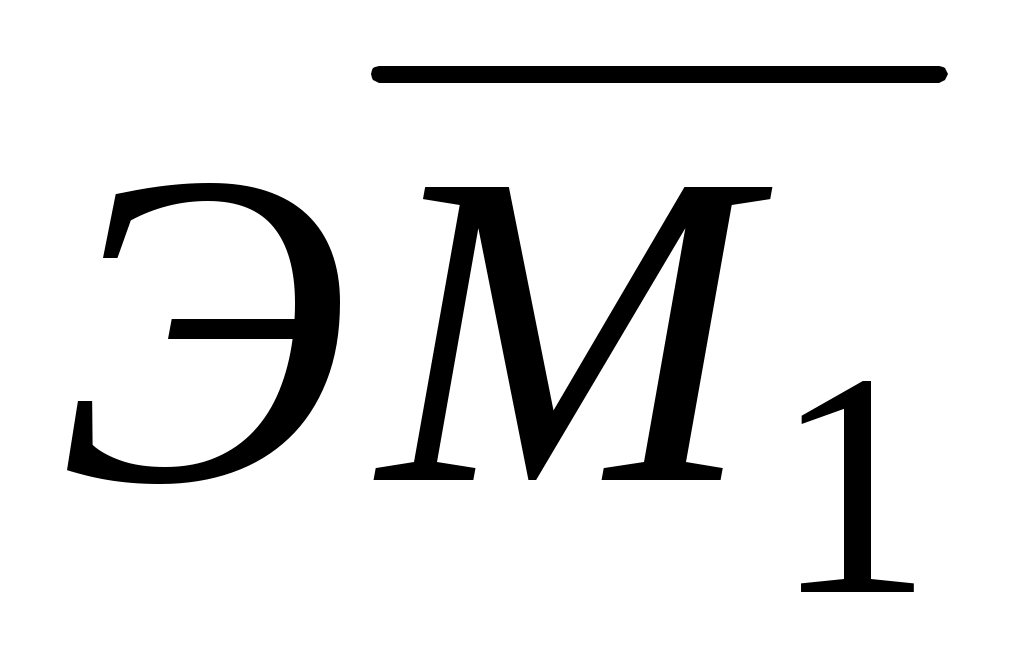 и
и 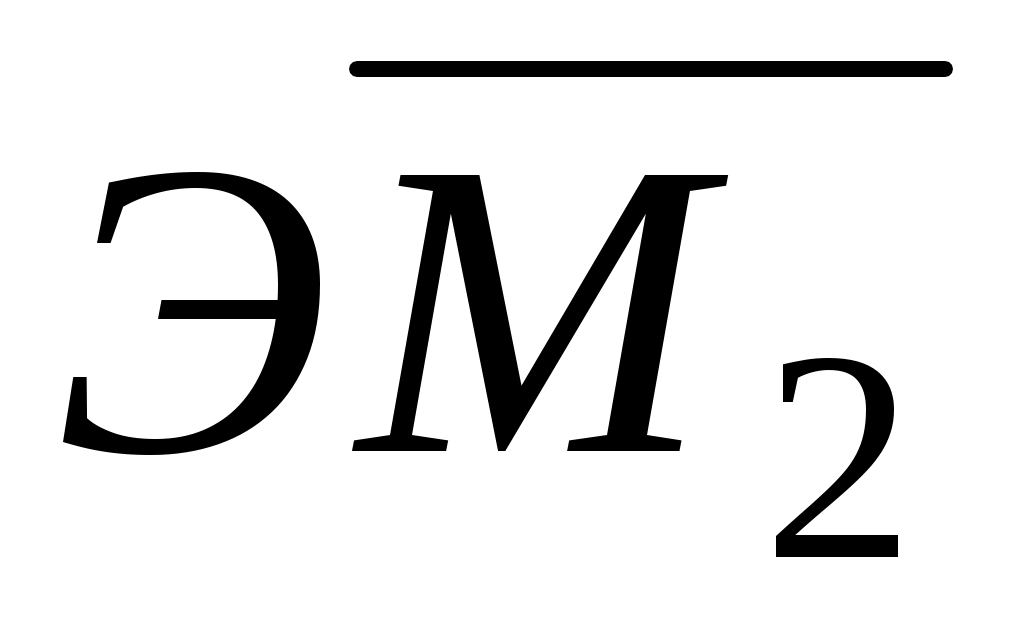 (индекс jсоответствует номеру “единичного” состояния, а i – номеру фигуры). Занесем значения iи
(индекс jсоответствует номеру “единичного” состояния, а i – номеру фигуры). Занесем значения iи  ji в табл. 5.1 (i =1, 2, 3, 4; j=1, 2).
ji в табл. 5.1 (i =1, 2, 3, 4; j=1, 2).
Таблица 5.1
Вычислим перемещения fyA и fyD:
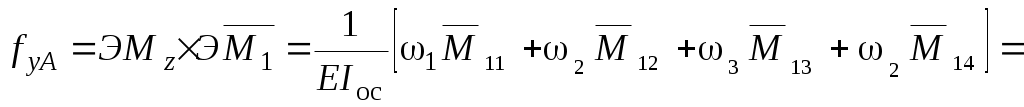
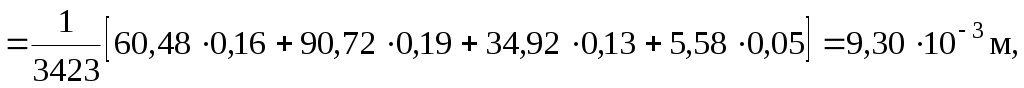
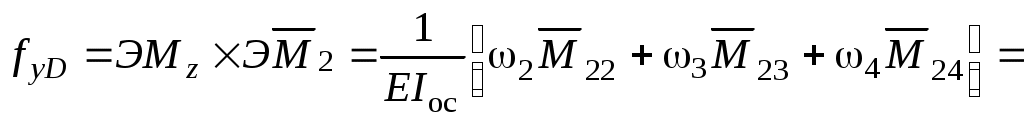
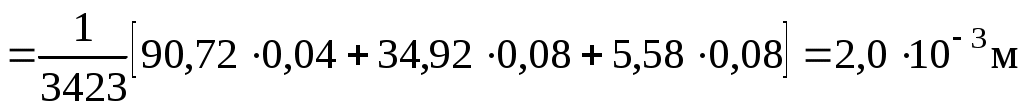 .
.
Горизонтальная плоскость. Разобьем эпюру изгибающих моментов ЭМy на элементарные фигуры , площади которых 5, 6, 7, 8 (рис. 5.4, е). Вычислим значения этих площадей, определим их положения центров тяжести с5, с6, с7, с8. Найдем ординаты ji, взятые под с5, с6, с7, с8 на эпюрах
ji, взятые под с5, с6, с7, с8 на эпюрах  и
и  . Занесем значения площадей iи ординат
. Занесем значения площадей iи ординат  ji в табл. 5.1 (i =5, 6, 7, 8; j=1, 2).
ji в табл. 5.1 (i =5, 6, 7, 8; j=1, 2).
Вычислим горизонтальные перемещения fzA и fzD:
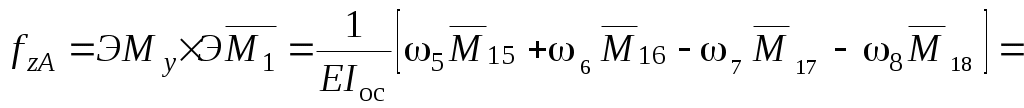
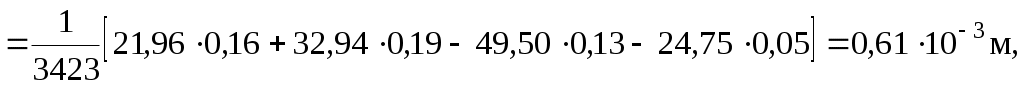
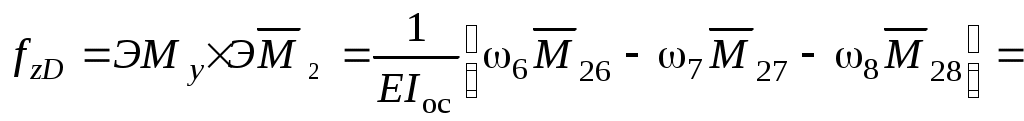
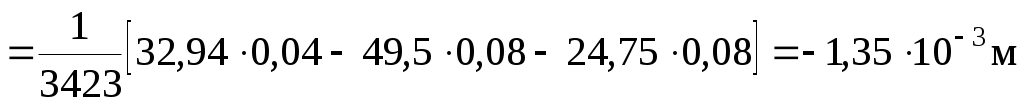 .
.
Найдем полные перемещения fA и fD в точках A и D:
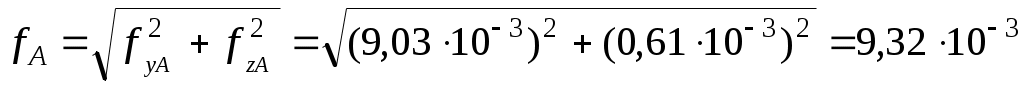 м,
м,
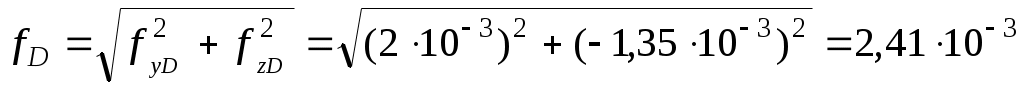 м.
м.
2.2. Расчет углов поворотов в опорах
Для определения угловых перемещений в сечениях С и В в приложим с этих сечениях единичные моменты М = 1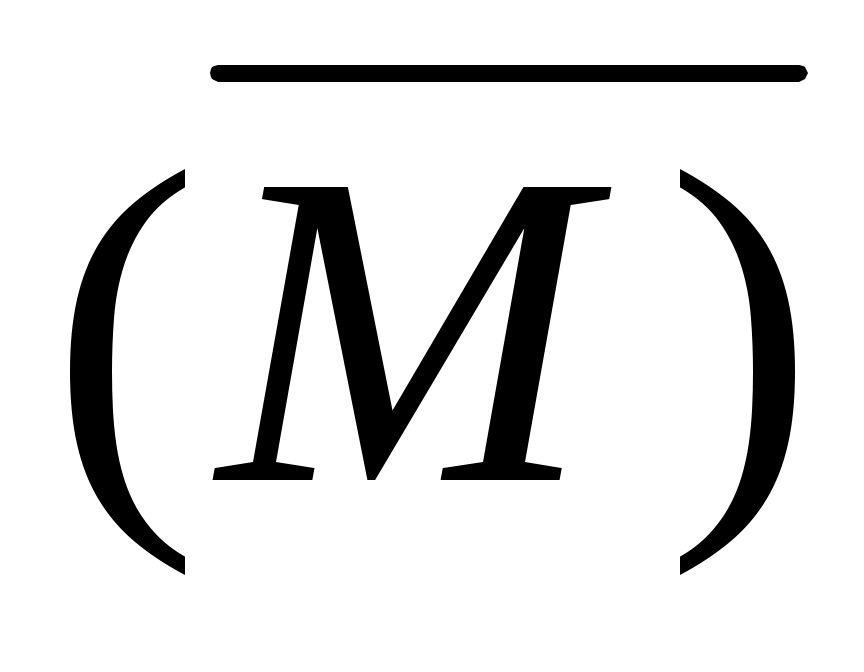
. Получим “единичные” состояния 3 и 4 (рис. 5.4, ж, з). Построим эпюры изгибающих моментов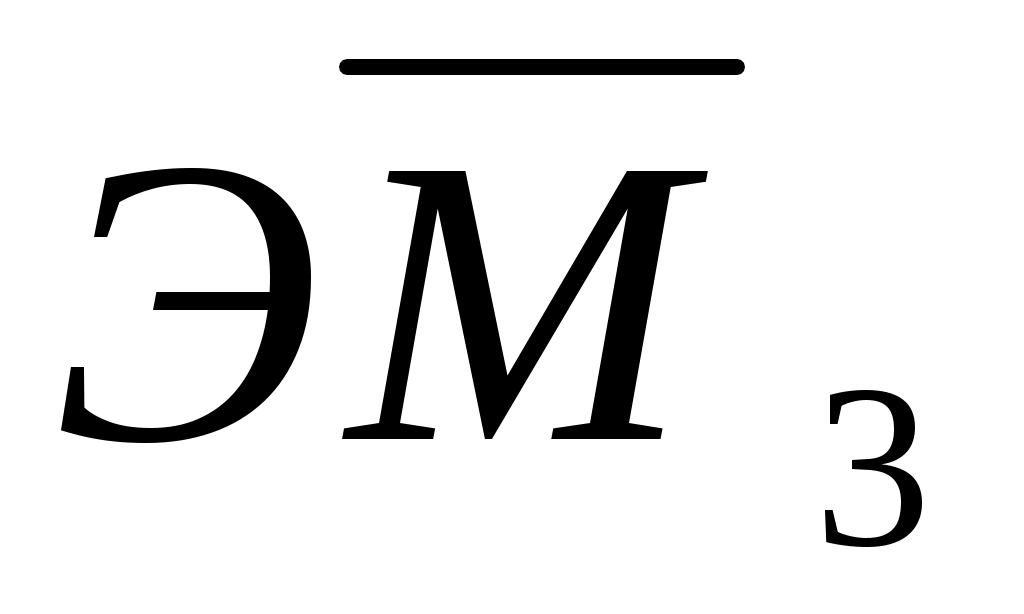 ,
, 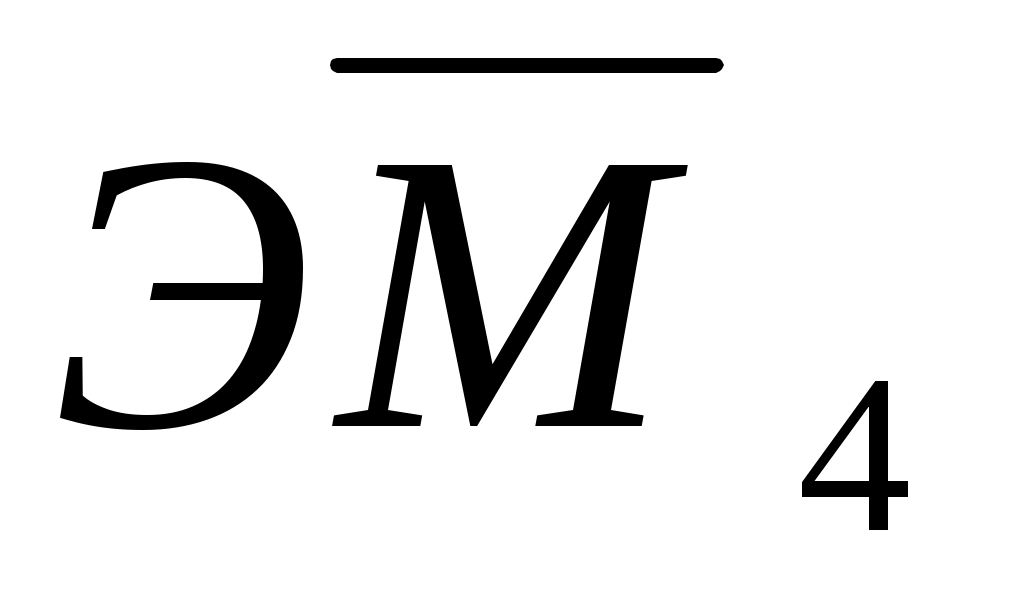 для этих состояний (рис. 5.4, и, к).
для этих состояний (рис. 5.4, и, к).
Вертикальная плоскость. Определим значения ординат ji на эпюрах
ji на эпюрах 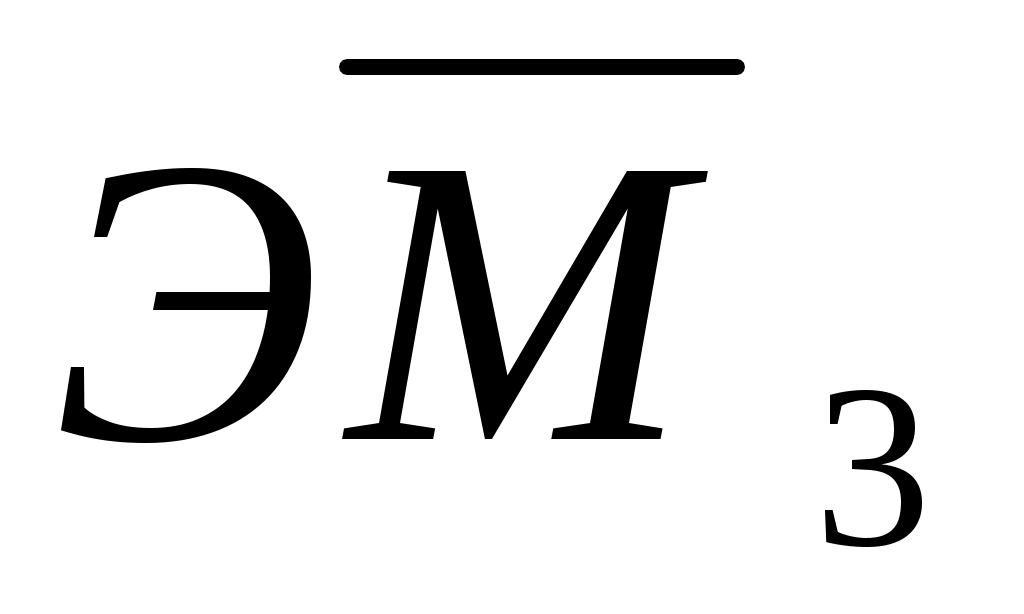 ,
, 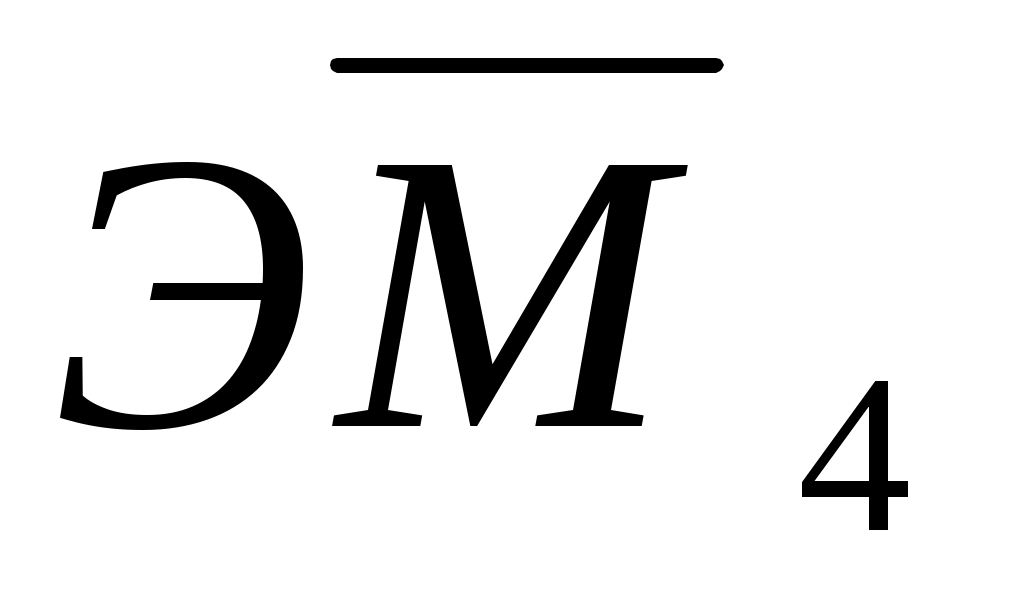 , взятых под центрами тяжести с1, с2, с3, с4 площадей 1, 2, 3, 4 эпюры ЭМz (рис. 5.4, и, к) и занесем их в табл. 5.1 (i =1, 2, 3, 4; j=3, 4).
, взятых под центрами тяжести с1, с2, с3, с4 площадей 1, 2, 3, 4 эпюры ЭМz (рис. 5.4, и, к) и занесем их в табл. 5.1 (i =1, 2, 3, 4; j=3, 4).
Угловые перемещения в сечениях С и В относительно оси z равны:
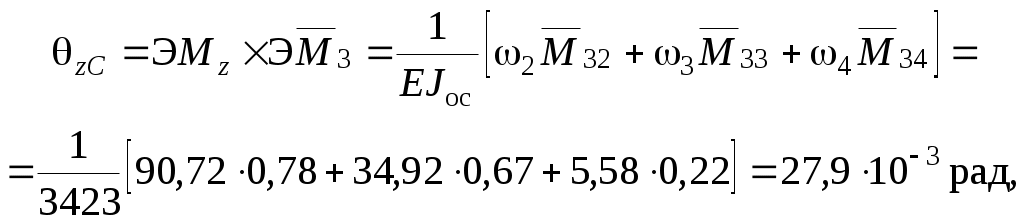
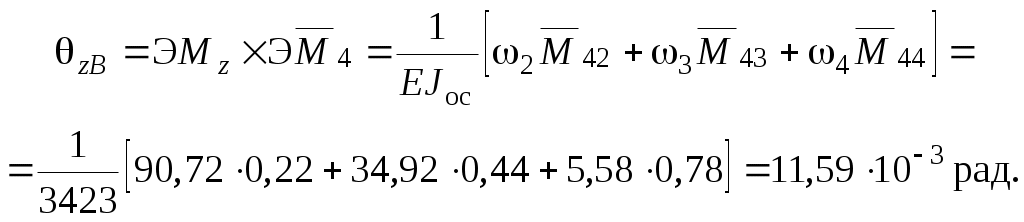
Горизонтальная плоскость. Найдем ординаты ji на эпюрах
ji на эпюрах 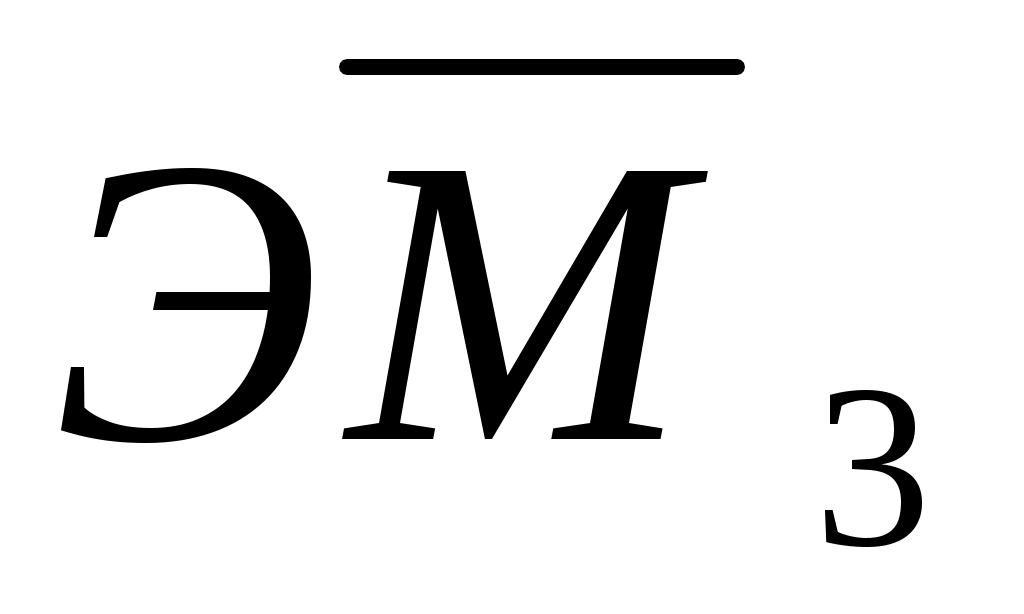 и
и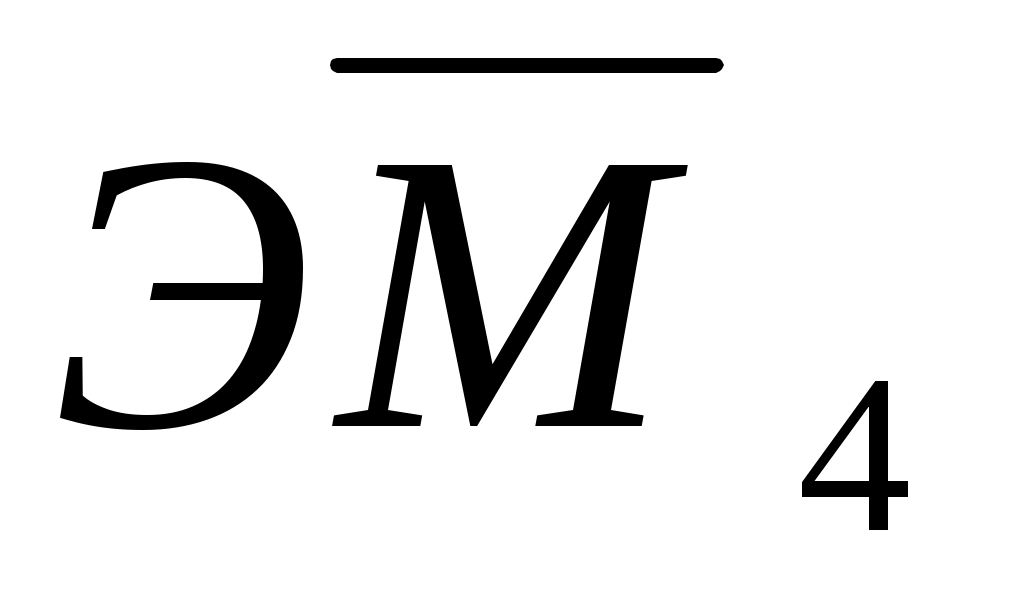 , взятые под с5, с6, с7, с8 . Занесем значения площадей iи ординат
, взятые под с5, с6, с7, с8 . Занесем значения площадей iи ординат  ji в табл. 5.1 (i =5, 6, 7, 8; j=3, 4).
ji в табл. 5.1 (i =5, 6, 7, 8; j=3, 4).
Вычислим угловые перемещения в сечениях С и В:
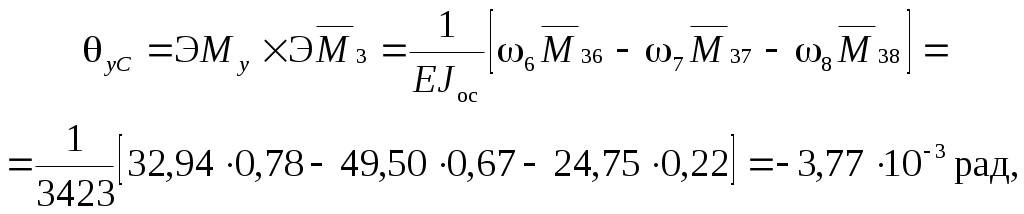
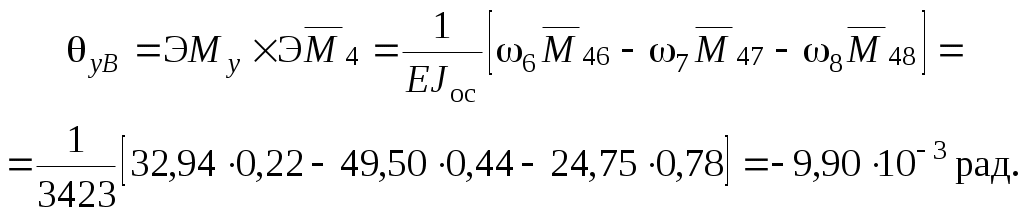
Найдем полные углы поворота в опорах:
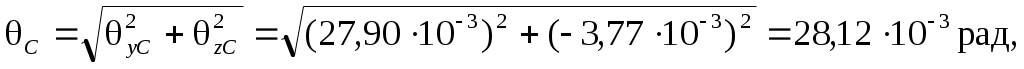
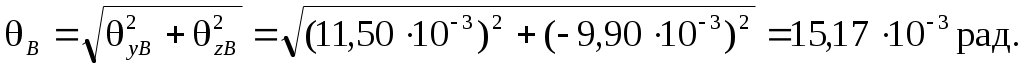
2.3 Расчет на изгибную жесткость. Уточнение диаметра вала.
Определим допускаемое значение прогибов [ f] = (1,0…5,0)10-4l0 , при l0 = 0,54 м примем [
f] = 3·10-4·0,54 = 1,62·10-4 м.
Будем считать, что в неподвижной опоре С установлен радиальноупорный шариковый подшипник, в подвижной В – радиальный роликовый. Тогда допускаемые углы поворота [B] = 0,005 рад, [C] = 0,0025 рад [см. прил.I, табл.2].
Проверим выполнение условий жесткости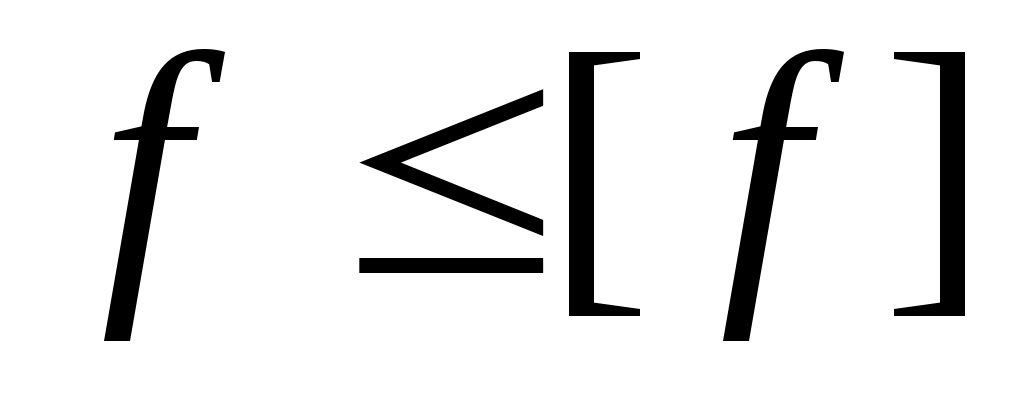 и
и 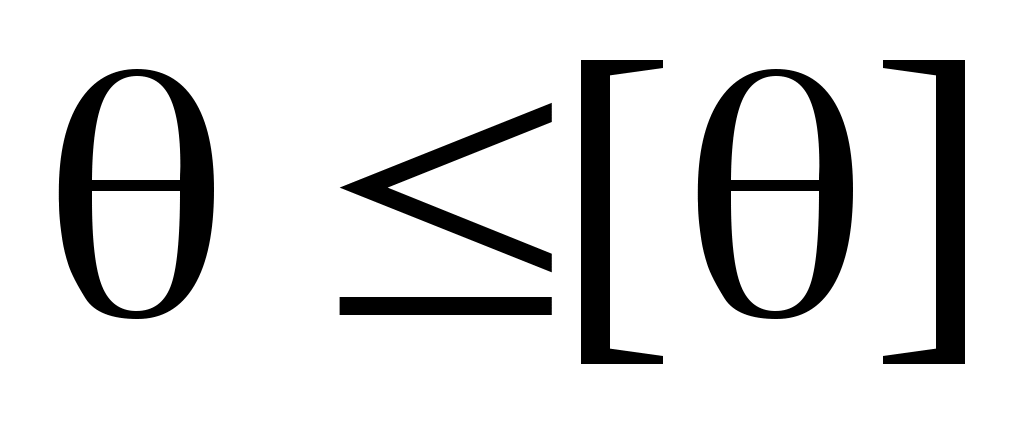 :
:
– в сечении А: fA = 9,32·10-3 м > [ f] = 1,62·10-4 м;
– в сечении D: fD = 2,41·10-4 м > [ f] = 1,62·10-4 м;
– в сечении C: C = 28,12·10-3 м > [] = 5·10-3 рад;
– в сечении В: В = 15,17·10-3 м > [] = 2,5·10-3 рад.
Видно, что условие жесткости не выполняется в сечении А и D по прогибам, а в сечении В и С по углам поворота. Уточним диаметр вала:
– в сечении А:
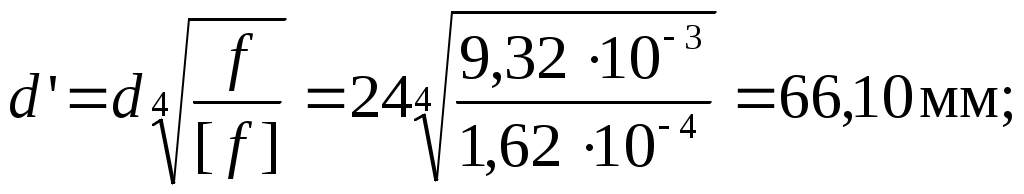
– в сечении С:
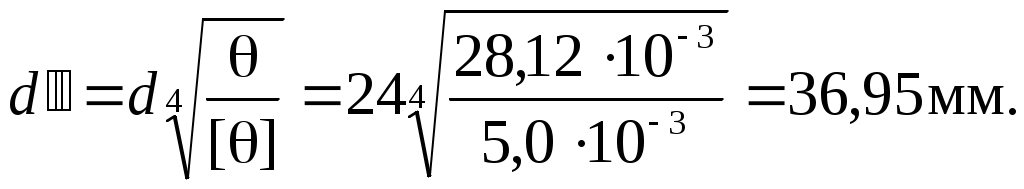
3. Расчет вала на усталостную прочность.
3.1 Выбор типа соединения в опасном сечении вала.
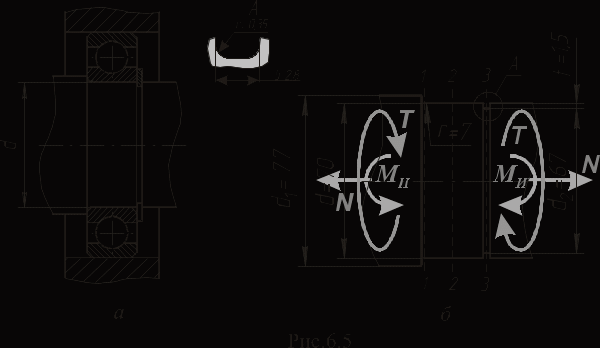
Опасное сечение находится в месте опоры С. Конструктивное оформление участка вала в месте посадки подшипника показано на рис.5.5, а.
Определим основные размеры вала в опасном сечении (рис. 5.5, б):
- диаметр упорного буртика d1 =(1,1…1,2)d=(1,1…1,2) 70=(77…84) мм;
- радиус галтельного перехода r=(0,1…0,2)d=(0,1…0,2)70=(7…14) мм;
- размеры канаки для установки стопорного кольца: ширина проточки b=(0,04…0,07)d=(0,04…0,07)70=(2,8…4,9) мм; глубина проточки t=(0,02…0,03)d=(0,02…0,03)70=(1,4…2,1) мм.
Примем: d1=77 мм, r=7 мм, b=2,8 мм, t=1,4 мм, r2=0,35 мм, d2=(d–
–2t)=(70 – 2∙1,4)=67 мм.
Характеристики материала 40ХНМА [3]: предел прочности в=(1100…1700) МПа; предел текучести Т=(850…1600) МПа; предел выносливости -1=(500…700) МПа; -1=(270…350) МПа. Примем в=1400МПа, Т=1150 МПа, -1 = 580 МПа, -1 = 314 МПа.
3.2 Определение числа расчетных сечений и концентраторов напряжений.
Концентраторами напряжений являются: галтельный переход (сечение 1-1), посадка подшипника с натягом (сечение 2-2), выточка для стопорного кольца (сечение 3- 3). Таким образом имеем три расчетных сечения.
3.3 Расчет характеристик цикла для нормальных и касательных напряжений в расчетных сечениях.
В опасном сечении вала действуют: нормальная сила N = 880 Н, изгибающий момент Ми = 536 Нм и крутящий момент Т = 420 Нм. В точках сечения возникают нормальные напряжения от изгиба и = Ми/Wос и растяжения N = N/A, а также касательные напряжения = T/Wp. При этом нормальные напряжения меняются по асимметричному циклу с амплитудой a = и и средним напряжением m = N, касательные напряжения по пульсирующему циклу a = m = /2.
Сечение 1-1. Геометрические характеристики сечения для диаметра d=70 мм: площадь
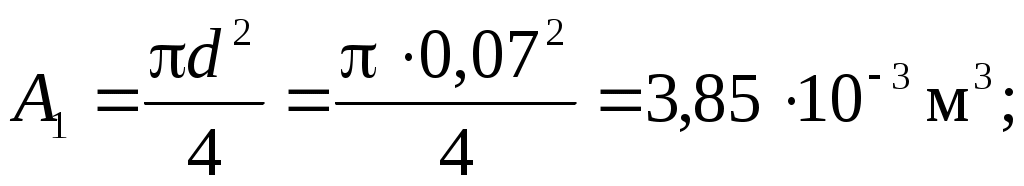
осевой момент сопротивления
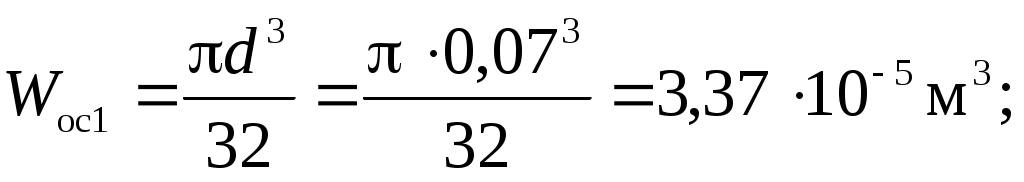
полярный момент сопротивления
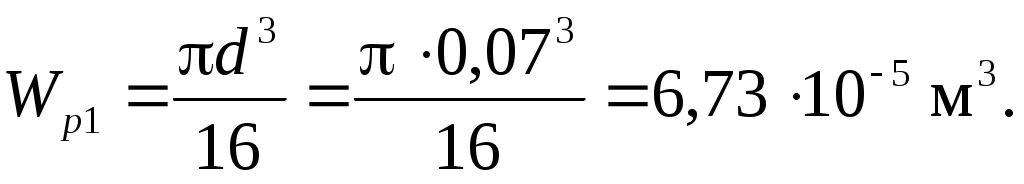
Так как в сечении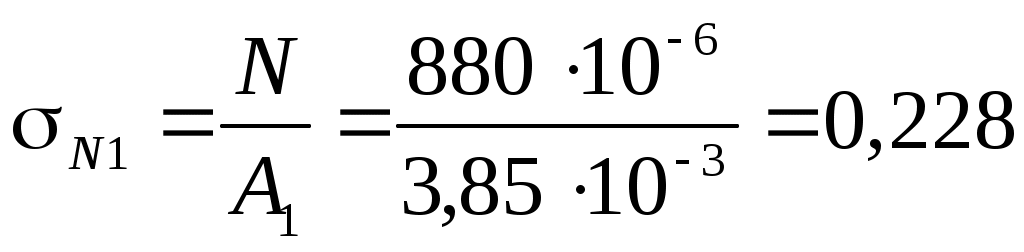 МПа, то нормальные напряжения меняются по асимметричному циклу с амплитудой
МПа, то нормальные напряжения меняются по асимметричному циклу с амплитудой
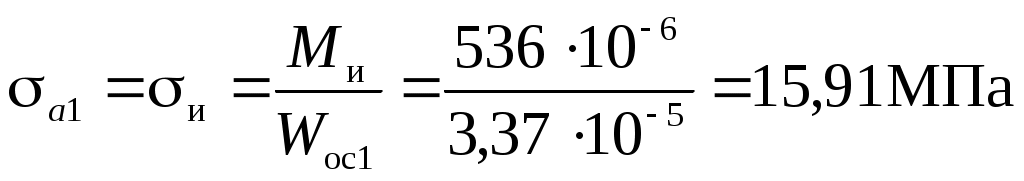
и средние значения
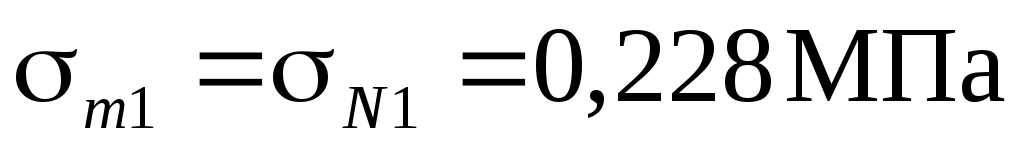 .
.
Касательные напряжения меняются по пульсирующему циклу:
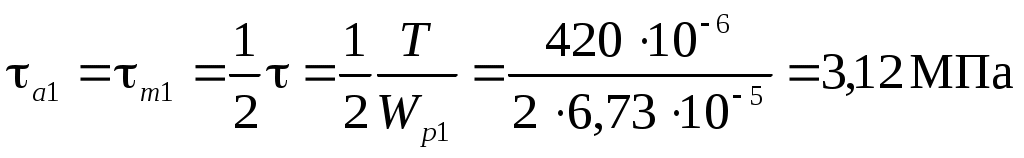 .
.
Сечение 2-2. Геометрические характеристики сечения для диаметра d=70 мм: площадь
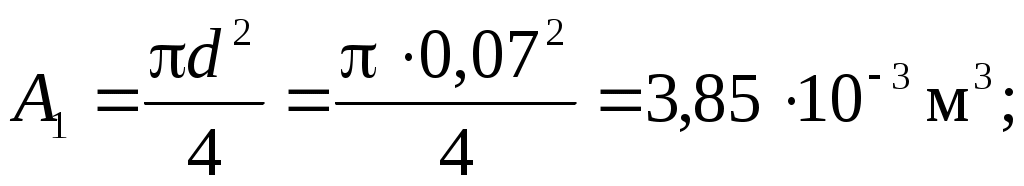
Разобьем эпюру изгибающих моментов ЭМz на элементарные фигуры, площади которых обозначим 1, 2, 3, 4 (рис. 5.4, д). Определим положения центров тяжести с1, с2, с3, с4 фигур. Вычислим значения площадей iи ординат
Таблица 5.1
| i | Площади фигур i, Нм2 | Ордината | |||
| Номер состояния j | |||||
| 1 | 2 | 3 | 4 | ||
| 1 | 60,48 | 0,16 | 0 | 0 | 0 |
| 2 | 90,72 | 0,19 | 0,04 | 0,78 | 0,22 |
| 3 | 34,92 | 0,13 | 0,08 | 0,67 | 0,44 |
| 4 | 5,58 | 0,05 | 0,08 | 0,22 | 0,78 |
| 5 | 21,96 | 0,16 | 0 | 0 | 0 |
| 6 | 32,94 | 0,19 | 0,04 | 0,78 | 0,22 |
| 7 | 49,50 | 0,13 | 0,08 | 0,67 | 0,44 |
| 8 | 24,75 | 0,05 | 0,08 | 0,22 | 0,78 |
Вычислим перемещения fyA и fyD:
Горизонтальная плоскость. Разобьем эпюру изгибающих моментов ЭМy на элементарные фигуры , площади которых 5, 6, 7, 8 (рис. 5.4, е). Вычислим значения этих площадей, определим их положения центров тяжести с5, с6, с7, с8. Найдем ординаты
Вычислим горизонтальные перемещения fzA и fzD:
Найдем полные перемещения fA и fD в точках A и D:
2.2. Расчет углов поворотов в опорах
Для определения угловых перемещений в сечениях С и В в приложим с этих сечениях единичные моменты М = 1
. Получим “единичные” состояния 3 и 4 (рис. 5.4, ж, з). Построим эпюры изгибающих моментов
Вертикальная плоскость. Определим значения ординат
Угловые перемещения в сечениях С и В относительно оси z равны:
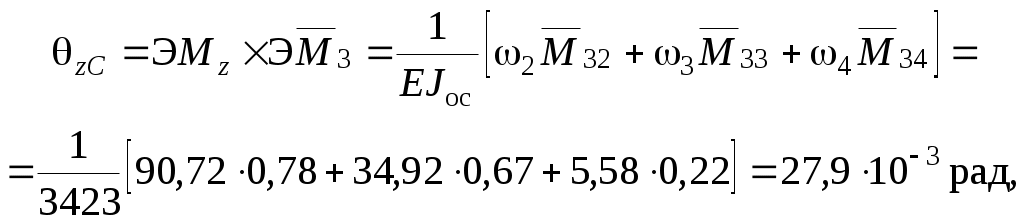
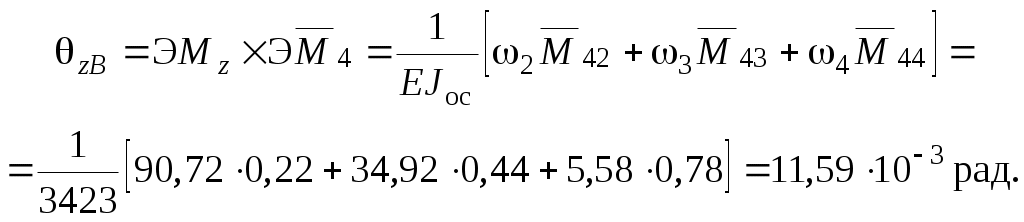
Горизонтальная плоскость. Найдем ординаты
Вычислим угловые перемещения в сечениях С и В:
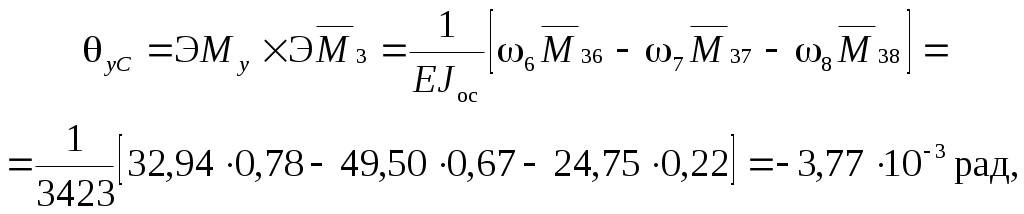
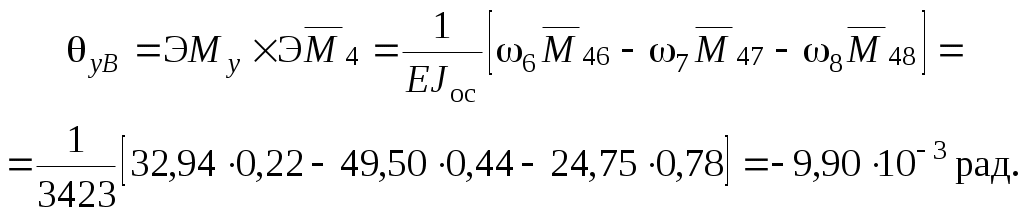
Найдем полные углы поворота в опорах:
2.3 Расчет на изгибную жесткость. Уточнение диаметра вала.
Определим допускаемое значение прогибов [ f] = (1,0…5,0)10-4l0 , при l0 = 0,54 м примем [
f] = 3·10-4·0,54 = 1,62·10-4 м.
Будем считать, что в неподвижной опоре С установлен радиальноупорный шариковый подшипник, в подвижной В – радиальный роликовый. Тогда допускаемые углы поворота [B] = 0,005 рад, [C] = 0,0025 рад [см. прил.I, табл.2].
Проверим выполнение условий жесткости
– в сечении А: fA = 9,32·10-3 м > [ f] = 1,62·10-4 м;
– в сечении D: fD = 2,41·10-4 м > [ f] = 1,62·10-4 м;
– в сечении C: C = 28,12·10-3 м > [] = 5·10-3 рад;
– в сечении В: В = 15,17·10-3 м > [] = 2,5·10-3 рад.
Видно, что условие жесткости не выполняется в сечении А и D по прогибам, а в сечении В и С по углам поворота. Уточним диаметр вала:
– в сечении А:
– в сечении С:
3. Расчет вала на усталостную прочность.
3.1 Выбор типа соединения в опасном сечении вала.
Опасное сечение находится в месте опоры С. Конструктивное оформление участка вала в месте посадки подшипника показано на рис.5.5, а.
Определим основные размеры вала в опасном сечении (рис. 5.5, б):
- диаметр упорного буртика d1 =(1,1…1,2)d=(1,1…1,2) 70=(77…84) мм;
- радиус галтельного перехода r=(0,1…0,2)d=(0,1…0,2)70=(7…14) мм;
- размеры канаки для установки стопорного кольца: ширина проточки b=(0,04…0,07)d=(0,04…0,07)70=(2,8…4,9) мм; глубина проточки t=(0,02…0,03)d=(0,02…0,03)70=(1,4…2,1) мм.
Примем: d1=77 мм, r=7 мм, b=2,8 мм, t=1,4 мм, r2=0,35 мм, d2=(d–
–2t)=(70 – 2∙1,4)=67 мм.

Характеристики материала 40ХНМА [3]: предел прочности в=(1100…1700) МПа; предел текучести Т=(850…1600) МПа; предел выносливости -1=(500…700) МПа; -1=(270…350) МПа. Примем в=1400МПа, Т=1150 МПа, -1 = 580 МПа, -1 = 314 МПа.
3.2 Определение числа расчетных сечений и концентраторов напряжений.
Концентраторами напряжений являются: галтельный переход (сечение 1-1), посадка подшипника с натягом (сечение 2-2), выточка для стопорного кольца (сечение 3- 3). Таким образом имеем три расчетных сечения.
3.3 Расчет характеристик цикла для нормальных и касательных напряжений в расчетных сечениях.
В опасном сечении вала действуют: нормальная сила N = 880 Н, изгибающий момент Ми = 536 Нм и крутящий момент Т = 420 Нм. В точках сечения возникают нормальные напряжения от изгиба и = Ми/Wос и растяжения N = N/A, а также касательные напряжения = T/Wp. При этом нормальные напряжения меняются по асимметричному циклу с амплитудой a = и и средним напряжением m = N, касательные напряжения по пульсирующему циклу a = m = /2.
Сечение 1-1. Геометрические характеристики сечения для диаметра d=70 мм: площадь
осевой момент сопротивления
полярный момент сопротивления
Так как в сечении
и средние значения
Касательные напряжения меняются по пульсирующему циклу:
Сечение 2-2. Геометрические характеристики сечения для диаметра d=70 мм: площадь