Файл: Расчет валов на статическую, усталостную прочность и жесткость Рекомендовано редакционноиздательским советом угату в качестве учебного пособия уфа 200 3.doc

• 
  среднее напряжение
  

.

(3.21)

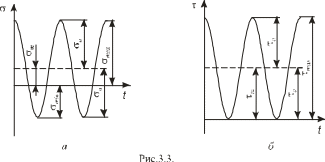
В течение срока службы вал испытывает многократное повторное нагружение и разгрузку, тогда касательные напряжения кручения меняются по пульсирующему циклу (рис. 3.3, б). Параметры такого цикла:

. (3.22)

Выбор расчетных коэффициентов. Коэффициенты k_, ; , ; , ; , , входящие в расчетные зависимости (3.18) для расчета , , выбираются для каждого расчетного сечения по таблицам или графикам, имеющимся в справочной литературе [2-5].

При этом можно также воспользоваться приведенными ниже рекомендациями, используемыми в практических расчетах.

Если имеются справочные данные по теоретическим коэффициентам концентрации напряжений (_ = _max/_ном, _ = _max/_ном), то эффективные коэффициенты концентрации напряжений k_, могут быть оценены согласно зависимости

k =1+q( - 1),

(3.23)

где q – коэффициент чувствительности материала к концентрации напряжений. Он принимается порядка:

---

q = 0,1…0,2 – для литых материалов; q = =0,2…0,4 – для малоуглеродистых сталей и жаропрочных деформируемых сплавов; q = 0,6…0,8 – для легированных сталей; q = 0,8…0,9 – для титановых сплавов; q = 0,3…0,5 – для алюминиевых сплавов.

Коэффициенты влияния состояния поверхностного слоя и могут быть приняты одинаковыми = = и представлены в виде

.

(3.24)

---

В этом произведении коэффициент учитывает влияние на усталостную прочность шероховатости поверхности детали. Он может быть принят: = 1,0 для полированной поверхности; =0,8…0,9 – для шлифованной; = 0,7…0,8 – для тонкого точения и = 0,6…0,7 – для грубого точения и фрезерования.

Коэффициент , учитывающий влияние коррозии, принимается: =1,0 при нормальной атмосфере; = 0,8…0,9 – при наличии следов коррозионного повреждения; = 0,5…0,8 – при эксплуатации детали в морской воде или агрессивной среде.

Коэффициент , характеризующий влияние на усталостную прочность технологического упрочнения поверхности, при наклепе берется порядка = 2,0…2,5; при химико-термической обработке – = 2,0…2,2.

Расчет коэффициентов запаса и оценка усталостной прочности. Для каждого из расчетных сечений по формулам (3.19), (3.18) рассчитываются коэффициенты запаса прочности n_, n_, n_экв, затем проверяется условие (3.17) усталостной прочности и делается необходимый вывод.

При недостаточной прочности вала даются рекомендации по ее повышению.

4	ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЩИТЕ РАБОТЫ

---

1. 
   Какие напряжения возникают в поперечном сечении стержня при изгибе с кручением?
   
2. 
   Как находятся опасные сечения стержня круглого сечения при изгибе с кручением?
   
3. 
   Какие точки круглого поперечного сечения являются опасными при изгибе с кручением? Какое напряженное состояние имеет место в этих точках?
   
4. 
   Как находится величина эквивалентного (приведенного) запаса прочности по различным теориям прочности при изгибе с кручением вала? Сделайте вывод соответствующих формул.
   
5. 
   Как производится расчет на статическую прочность при изгибе с кручением?
   
6. 
   Как оценивается жесткость вала?
   
7. 
   Как находится полный прогиб вала в месте посадки дисков (колес)?
   
8. 
   Как находится полный угол поворота в опоре вала?
   
9. 
   Какими способами могут быть вычислены обобщенные перемещения?
   
10. 
    Как устанавливаются допускаемые значения обобщенного перемещения?
    
11. 
    Что такое действительное (или грузовое) и единичное (или фиктивное) состояние?
    
12. 
    Как производится перемножение эпюр по правилу Верещагина?
    
13. 
    Как по правилу Верещагина производится перемножение эпюр, ограниченных ломаными линиями?
    
14. 
    Какими величинами характеризуется цикл изменения напряжений? Что такое симметричный и асимметричный циклы?
    
15. 
    Что такое кривая усталости (кривая Велера) и как ее строят?
    
16. 
    Что называют пределом усталости (выносливости)?
    
17. 
    Как влияют размеры детали на величину предела усталости? Что такое масштабный фактор и от чего он зависит?
    
18. 
    Что такое эффективный коэффициент концентрации напряжений и коэффициент чувствительности материала к концентрации напряжений? Как они связаны между собой и от каких факторов зависят?
    
19. 
    Как влияет на величину предела усталости характер обработки поверхности детали? Что называется коэффициентом качества поверхности?
    
20. 
    Какой вид имеет условие усталостной прочности?
    
21. 
    Как определяется коэффициент запаса прочности при симметричном и асимметричном циклах в случаях растяжения, сжатия, кручения и изгиба?
    
22. 
    Как определяется коэффициент запаса усталостной прочности вала, работающего на совместное действие изгиба с кручением?
    

5	ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ

---

ЗАДАНИЕ. На вал АВ установлены два зубчатых колеса диаметрами D₁ и D₂, нагруженные усилиями от сопряженных колес (рис 5.1, а).

Необходимо:

- подобрать диаметр вала d из условия статической прочности. В опасном сечении вала построить эпюры нормальных и касательных напряжений и показать напряженное состояние тела в опасной точке.

- произвести расчет вала на жесткость по линейным перемещениям в местах установки колес и по угловым перемещениям в опорах. Уточнить диаметр вала.

- выполнить проверочный расчет вала на усталостную прочность в опасном сечении (рис. 5.1, б, в).


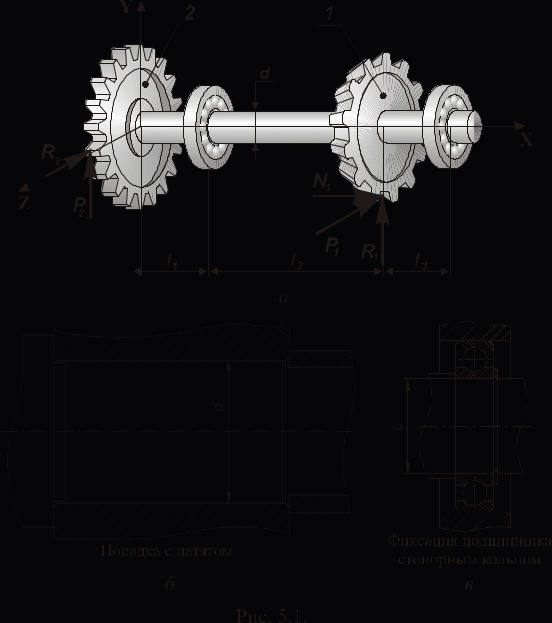
Исходные расчетные данные

N1, кН	R1, кН	P1, кН	l1, м	l2, м	l3, м	D1, м	D2, м	Марка стали
0,88	0,51	2,80	0,24	0,36	0,18	0,30	0,40	40ХНМА

1. 
   проектировочный расчет вала на статическую прочность
   

0. 
   Построение расчетной схемы вала
   

При расчете на статическую прочность представим вал АВ в виде балки на двух опорах. Одну из опор примем шарнирно – неподвижной (сечение С), другую, как наиболее близко расположенную к коническому колесу, - шарнирно – подвижной (сечение В, рис. 5.2, а).

Заменим действие установленных на вал колес соответствующими нагрузками. Векторы радиальных сил R₁ и R₂ перенесем в центр тяжести сечения вала по линии их действия. Векторы окружных сил P₁ и P₂ – параллельно самим себе. При этом появятся два крутящих сосредоточенных момента



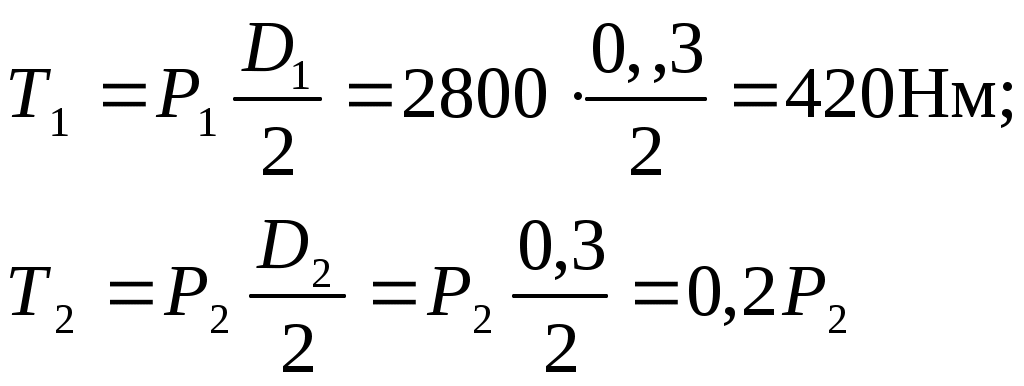
в сечениях A и D соответственно.

Для определения окружного усилия Р₂ запишем уравнение статического равновесия в виде суммы моментов всех сил, действующих на вал, относительно продольной оси

---