ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 957
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
и SM», «SК конъюнкция SM»).
1. Функция готовности Г(t) системы определяет вероятность нахождения системы в работоспособном состоянии в момент t:
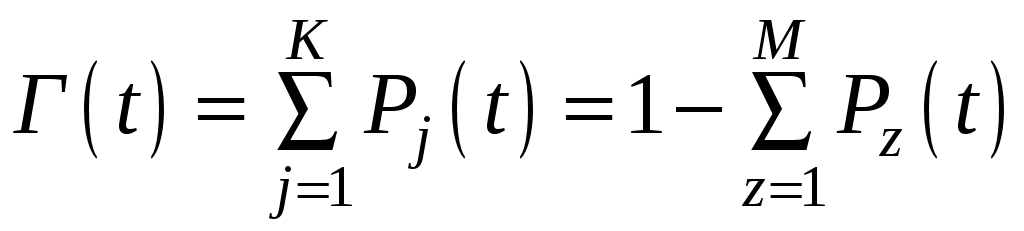, (4.42)
где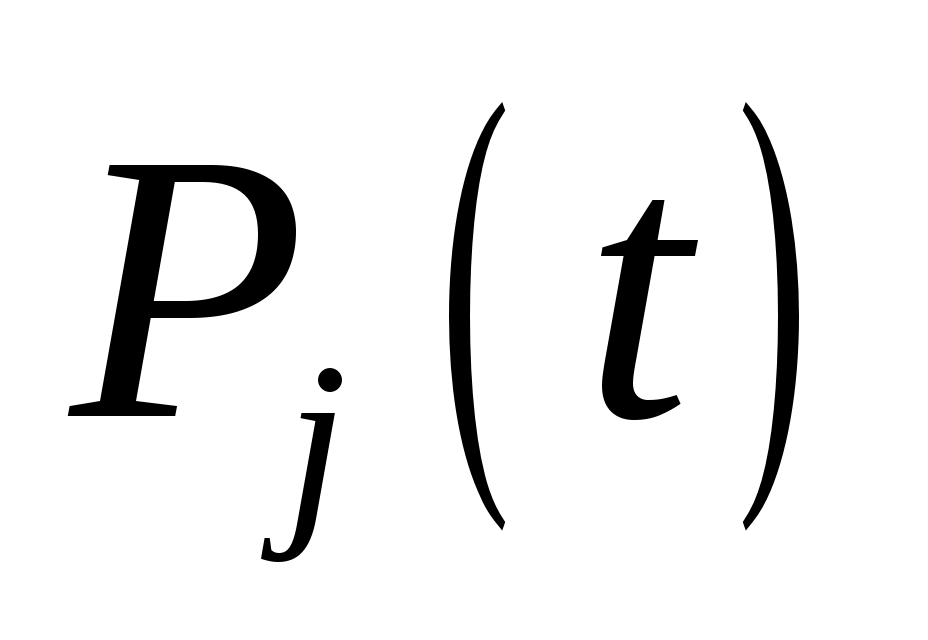
– вероятность нахождения системы в работоспособном j-м состоянии;
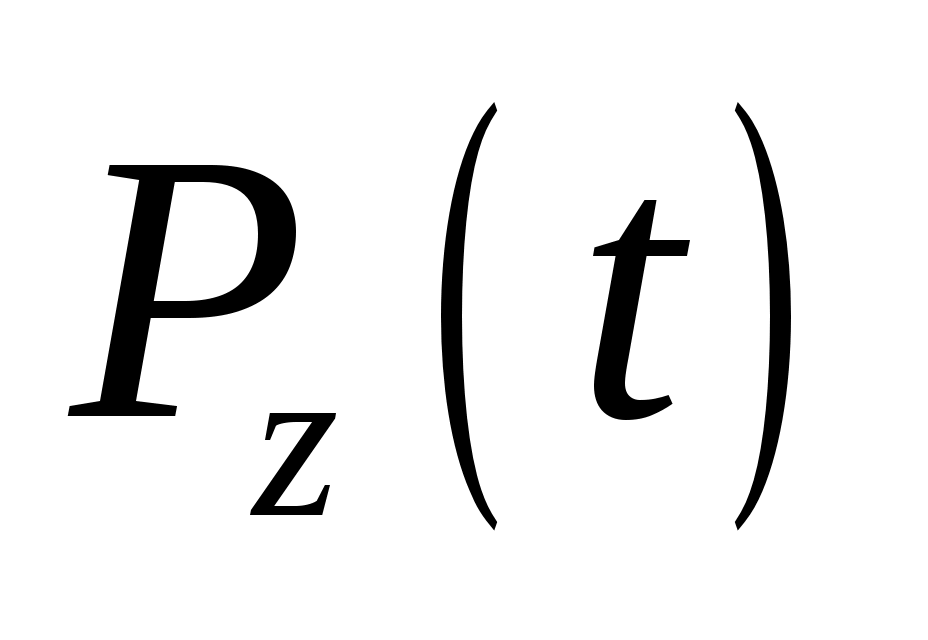– вероятность нахождения системы в неработоспособном z-м состоянии.
2. Функция простоя П(t) системы:
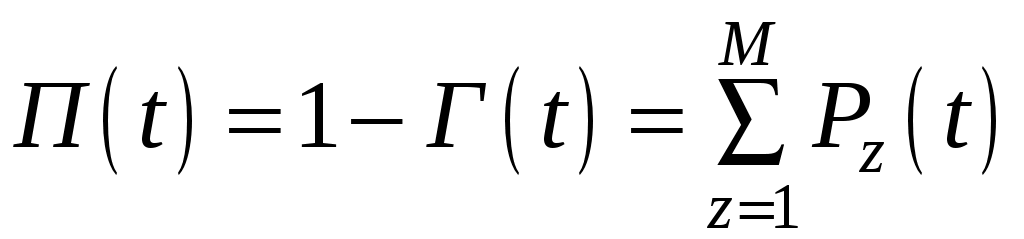. (4.43)
3. Коэффициент готовности kг.ссистемы определяется при установившемся режиме эксплуатации (при t ∞). При t ∞ устанавливается предельный стационарный режим, в ходе которого система переходит из состояния в состояние, но вероятности состояний уже не меняются:
; 
.
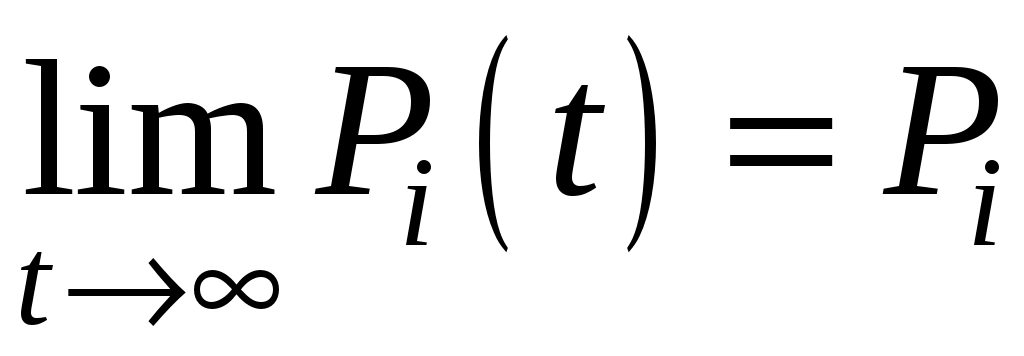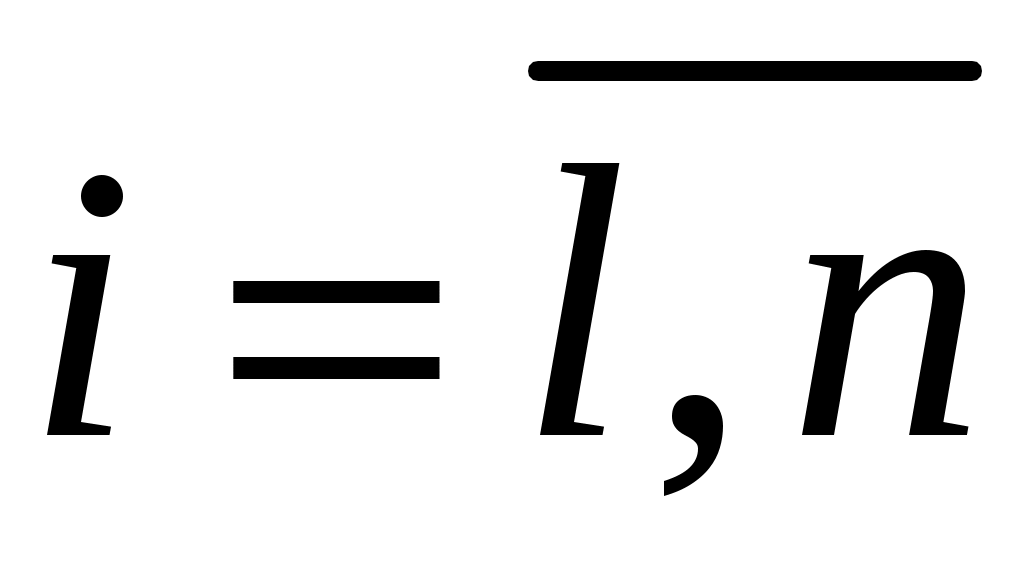Коэффициент готовности kг.сможно рассчитать по системе (4.41) дифференциальных уравнений, приравнивая нулю их левые части dPi(t) / dt = 0, так как Pi= const при t ∞. Тогда система уравнений (4.41) превращается в систему алгебраических уравнений вида:
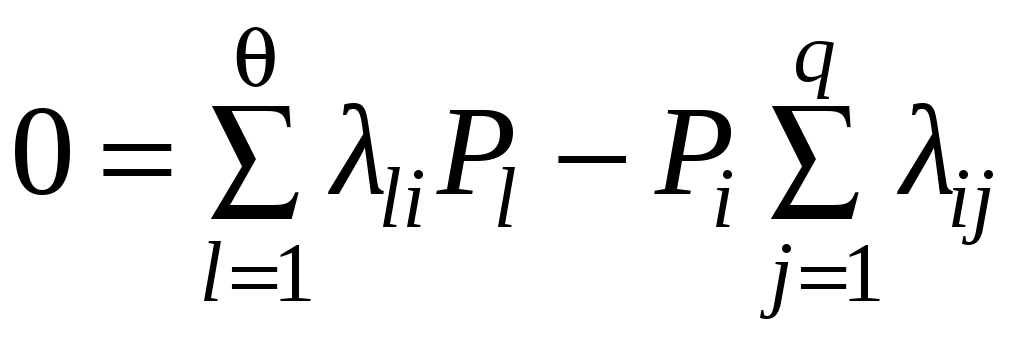, (4.44)
и коэффициент готовности
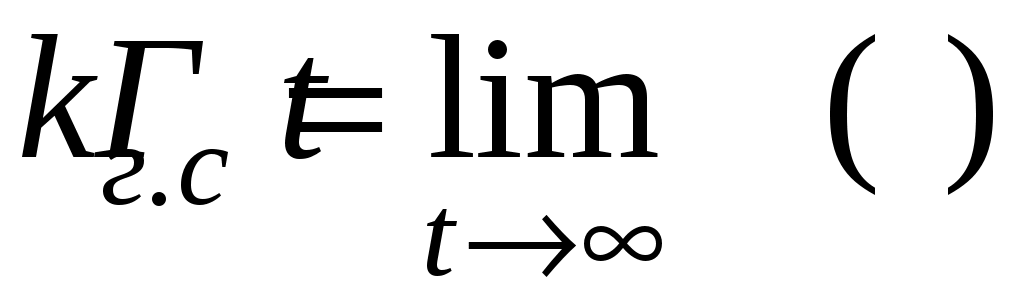(4.45)
есть предельное значение функции готовности при установившемся режиме t→∞.
4. Параметр потока отказов системы:
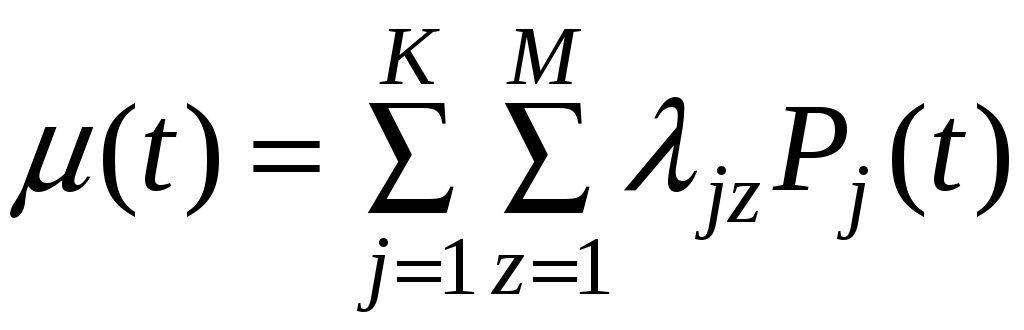, (4.46)
где λjz – интенсивности (обобщенное обозначение) переходов из работоспособного состояния в неработоспособное.
5. Функция потока отказов:
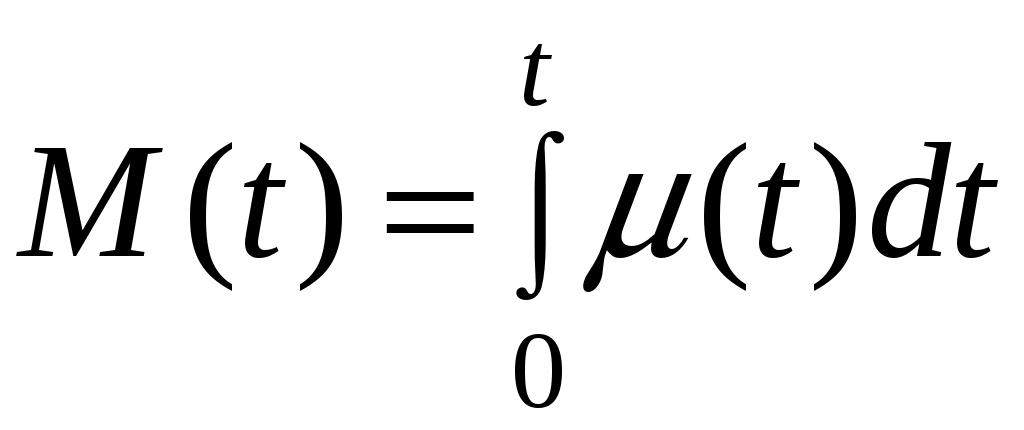. (4.47)
6. Средняя наработка между отказами на интервале t:
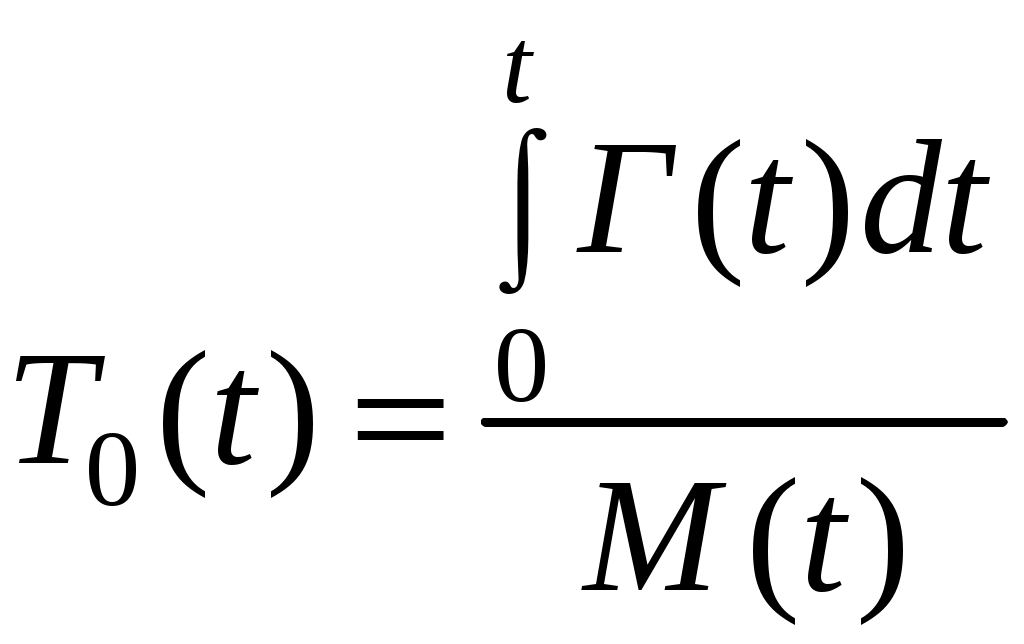. (4.48)
Примечание: при t → ∞, когда Pj
(t = ∞) = Pj(∞) = Pj, средняя наработка между отказами T0= kг.с / μ, где µ(∞) = µ.
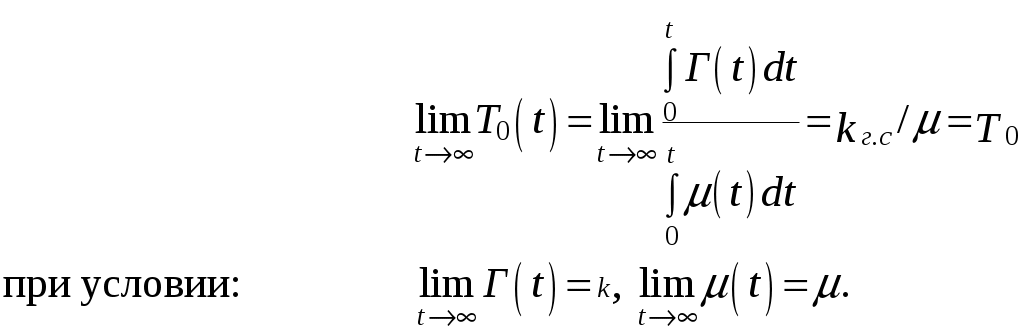
В качестве примера вычисления показателей надежности рассмотрен восстанавливаемый объект, у которого поток отказов простейший (пуассоновский) с параметром потока
μ = λ= 1/ T , (4.49)
а распределение времени восстановления подчиняется экспоненциальному распределению с интенсивностью восстановления
μ = 1/ TВ ,(4.50)
где T – средняя наработка между отказами; TВ – среднее время восстановления.
С
λ
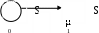остояния элемента: S0 – работоспособное; S1 – неработоспособное
(рис. 4.16); Р0(t) – вероятность работоспособного состояния при t; P1(t) – вероятность неработоспособного состояния при t.
µ
λ
Рис. 4.16. Граф состояний восстанавливаемого объекта
Система дифференциальных уравнений:
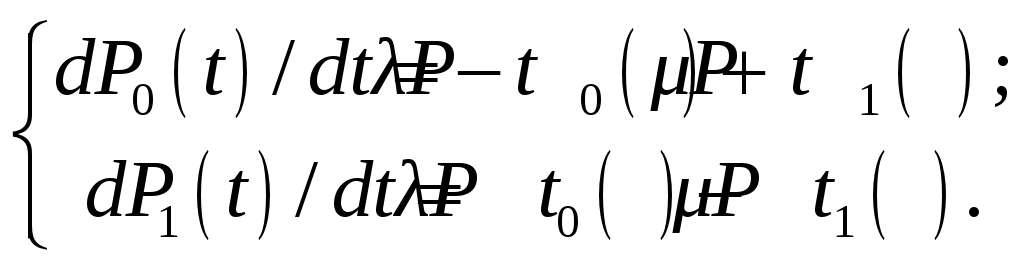(4.51)
Начальные условия: при t = 0 P0(t = 0) = P0(0) = 1; P1(0) = 0.
Поскольку состояния S0и S1представляют полную группу событий, то
P0(t) + P1(t) = 1. (4.52)
Путём выражения P0(t) = 1 – P1(t) и подстановки в (4.51) получено одно дифференциальное уравнение относительно P1(t):
dP1(t)/dt = λ(1 – P1(t)) – μP1(t). (4.53)
Решение уравнения производится с использованием преобразования Лапласа. Преобразование Лапласа для вероятностей состояния
Pi(t):
,
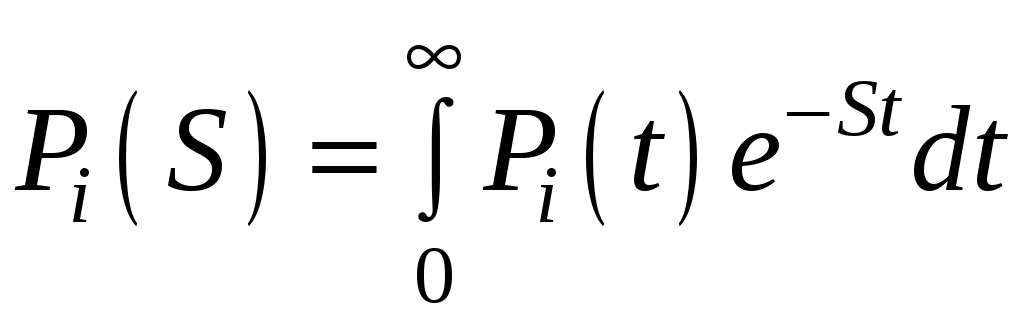где Pi(S) = L{Pi(t)} – изображение вероятности Pi(t).
Преобразование Лапласа для производной dPi(t)/dt:
.
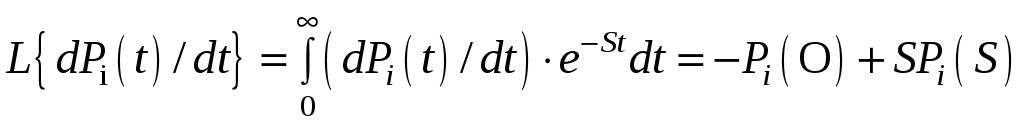После применения преобразования Лапласа к левой и правой частям уравнения получено уравнение изображений:
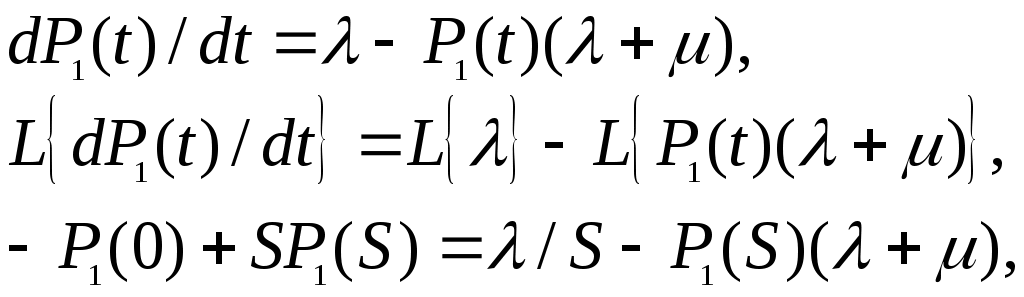
где L{λ} = λ L{1} = λ / S.
При P1(0) = 0
SP1(S) + P1(S)(λ + μ) = λ / S,
P1(S)(S + λ + μ) = λ / S.
Преобразованием приведенных соотношений получено выражение вероятности нахождения объекта в неработоспособном состоянии:
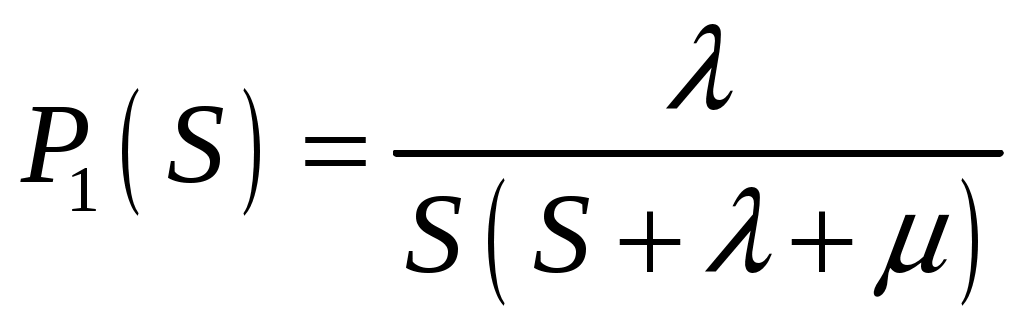. (4.54)
Введение обозначения λ + μ = а позволяет преобразовать правую часть выражения (4.54):
.
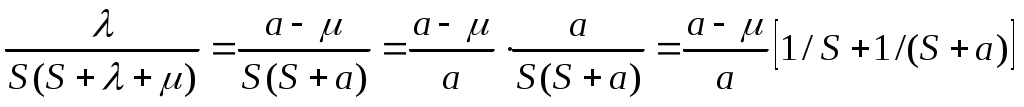Применяя обратное преобразование Лапласа, с учётом L{f(t)} = 1/S,
а также f(t) = 1; L{f(t)} = 1/(S + a), получают f(t) = e–at, после чего находят вероятность пребывания объекта в неработоспособном состоянии в виде выражения:
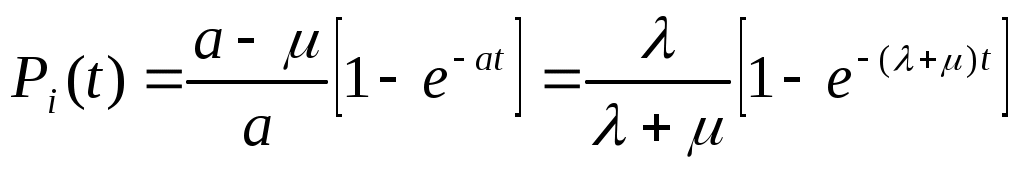. (4.55)
Тогда вероятность нахождения в работоспособном состоянии
P0(t) = 1 – P1(t) равна:
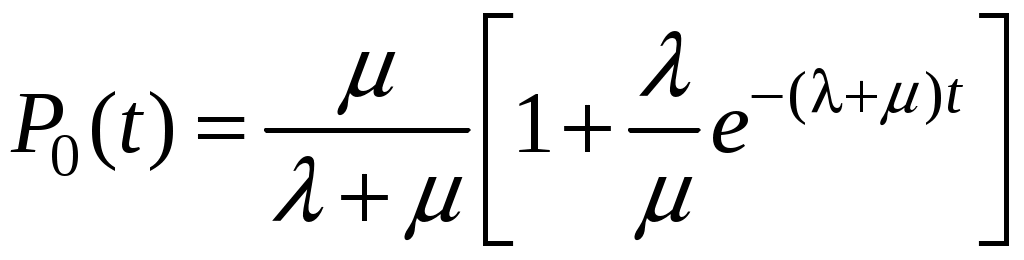. (4.56)
С помощью полученных выражений можно рассчитать вероятность работоспособного состояния и отказа восстанавливаемого объекта в любой мо- мент t.
Коэффициент готовности системы kг.с определяется при установившемся режиме t ∞, при этом Pi(t) = Pi = const, поэтому составляется система алгебраических уравнений с нулевыми левыми частями, поскольку dPi(t)/dt = 0.
Так как kг.с есть вероятность того, что система окажется работоспособной в момент t при t ∞, то из полученной системы уравнений определяется
P0 = kг.
с .
При t ∞ алгебраические уравнения имеют вид:
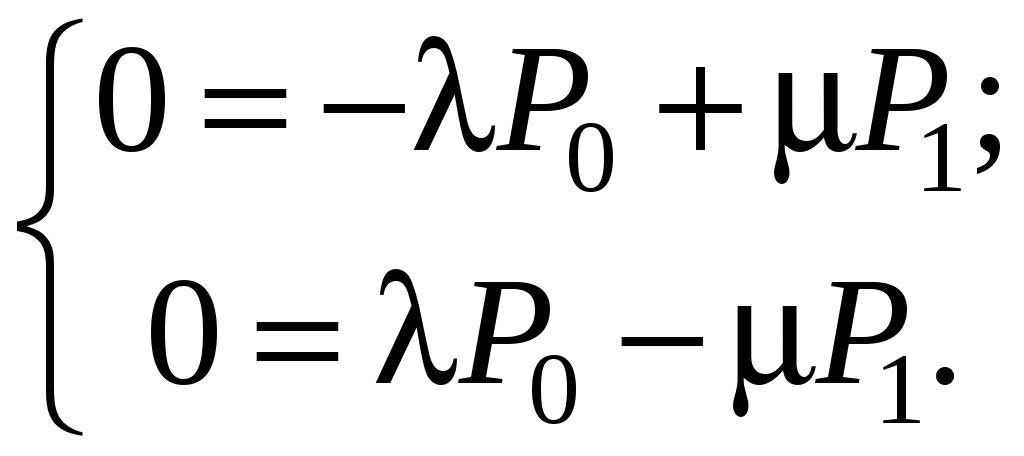(4.57)
Дополнительное уравнение: P0+ P1 = 1.
При P1 = 1 – P0 получается 0 = λP0 – μ(1 – P0), или μ = P0(λ + μ),
откуда
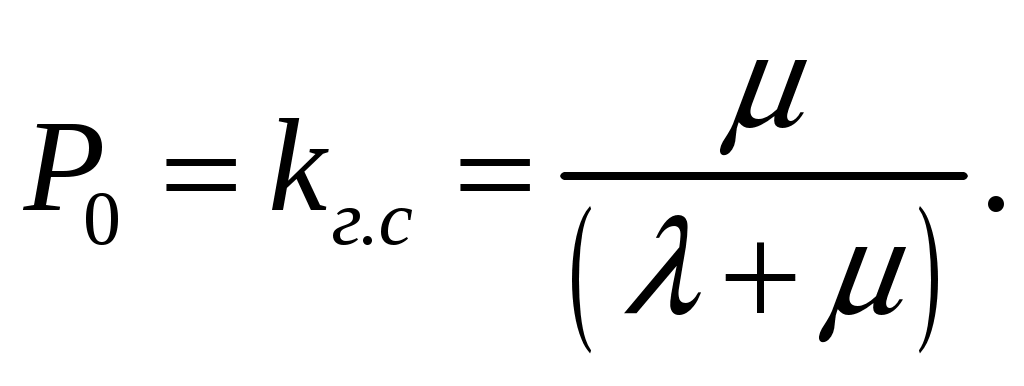(4.58)
Остальные показатели надежности восстанавливаемого элемента:
– функция готовности Г(t) = P0(t);
– функция простоя П(t) = 1 – Г(t) = P1(t);
– параметр потока отказов µ(t) = λP0(t) = λГ(t),
при t ∞ (стационарный установившийся режим восстановления)
µ(t) = µ(∞) = µ = λP0 = λkг.с;
– ведущая функция потока отказов
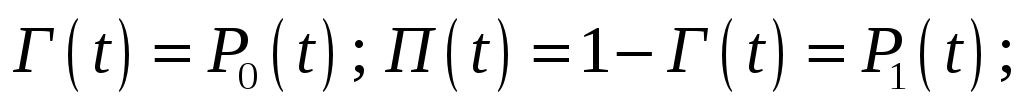
– средняя наработка между отказами t0= kг.с / μ = kг.с /kг = 1/λ.
Метод дифференциальных уравнений может быть использован для расчёта показателей надёжности и невосстанавливаемых объектов (систем).
В этом случае неработоспособные состояния системы являются «поглощающими» и интенсивности λ выхода из этих состояний исключаются.
Для невосстанавливаемого объекта граф состояний имеет вид (рис. 4.17):
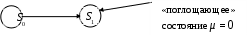
Рис. 4.17. Граф состояний невосстанавливаемого объекта
Система дифференциальных уравнений для данного объекта:
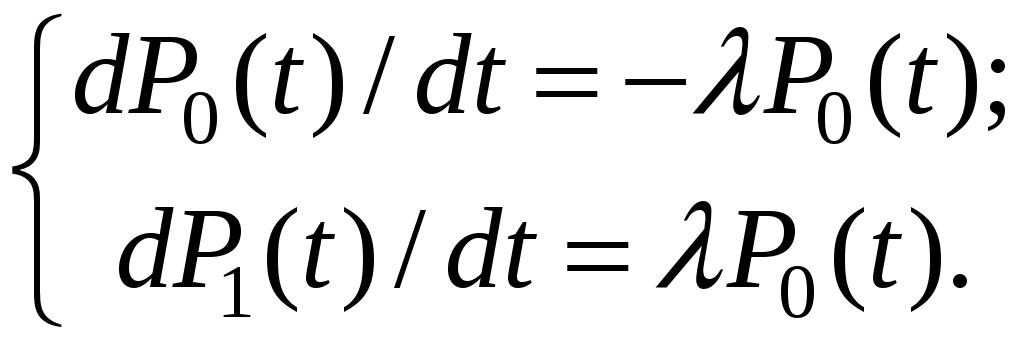
Начальные условия: P0 (0) = 1; P1(0) = 0.
Изображение по Лапласу первого уравнения системы:
;
.
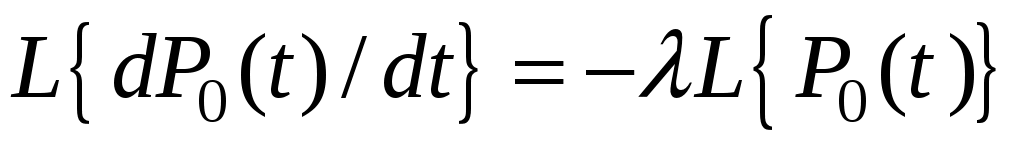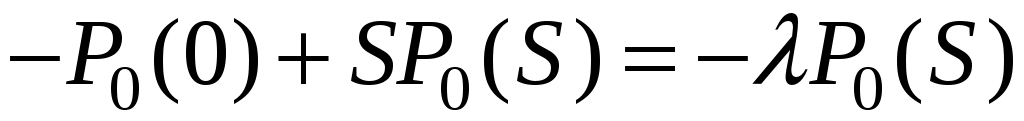После группировки: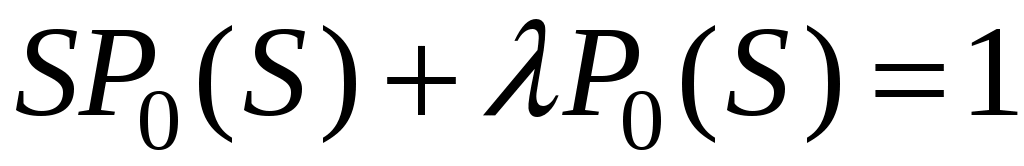
;
,
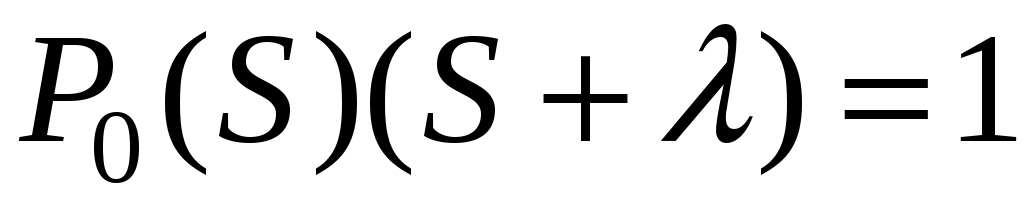откуда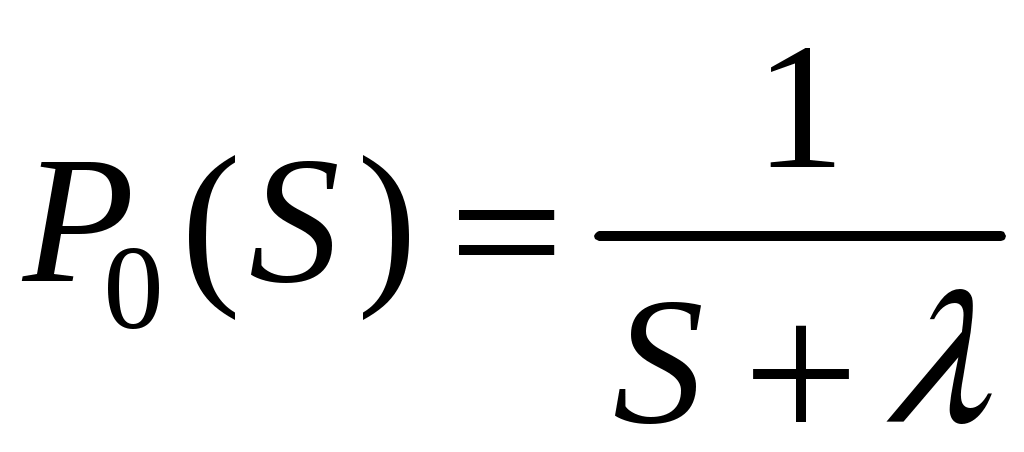
.
Используя обратное преобразование Лапласа, получают
.
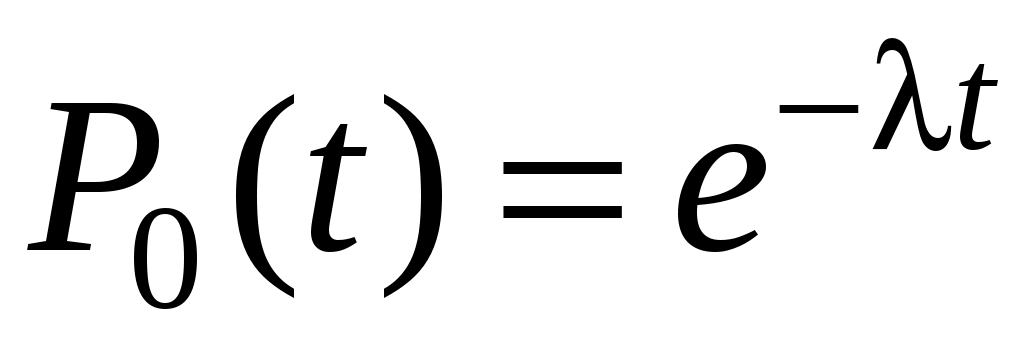4.5.2. Связь логической схемы надёжности с графом состояний
Переход от логической схемы к графу состояний необходим:
– при смене методов расчёта надёжности и сравнении результатов;
– для оценки выигрыша в надёжности при переходе от невосстанавливаемой системы к восстанавливаемой.
Рассматриваются типовые логические структуры надежности. Для невосстанавливаемых систем граф – однонаправленный, переходы характеризуются интенсивностями отказов λ.
Для восстанавливаемых систем в графах состояний добавляются обратные стрелки, соответствующие интенсивностям восстановлений В (табл. 4.4).
Таблица 4.4
Типовые логические структуры надёжности
Структурная
логическая
схема
Графы состоний
Элементы различной надежности
Равнонадежные
элементы
Обозначения на графах состояний:
1 – работоспособное состояние элемента,
0 – неработоспособное состояние элемента.
Контрольные вопросы
1. В чём особенности марковского случайного процесса, на основе которого строится расчётная модель для восстанавливаемых объектов и систем?
2. Назовите основные этапы составления расчётной модели.
3. Поясните мнемоническое правило составления дифференциального уравнения вероятностей состояния (уравнение Колмогорова – Чепмена).
4. Дайте определение и поясните смысл показателей надежности восстанавливаемых объектов и систем.
5. Каковы особенности применения метода дифференциальных уравнений для расчета надежности невосстанавливаемых объектов?
6. На любом из примеров поясните связь графа состояний с логической структурой надёжности.
4.6. Пример расчёта безотказности
с использованием модели «прочность – нагрузка»
1. Рассчитать элемент, на который действует растягивающая нагрузка (рис. 4.18).
Принимается, что растягивающая нагрузка
1. Функция готовности Г(t) системы определяет вероятность нахождения системы в работоспособном состоянии в момент t:
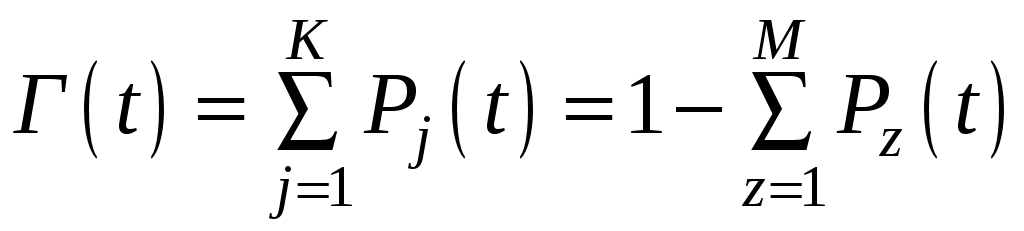, (4.42)где
– вероятность нахождения системы в работоспособном j-м состоянии; – вероятность нахождения системы в неработоспособном z-м состоянии.2. Функция простоя П(t) системы:
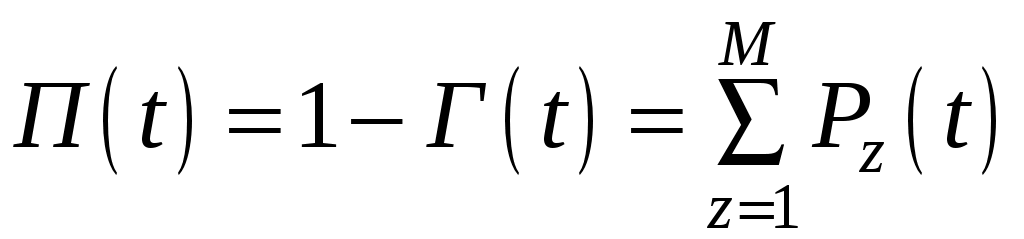. (4.43)3. Коэффициент готовности kг.ссистемы определяется при установившемся режиме эксплуатации (при t ∞). При t ∞ устанавливается предельный стационарный режим, в ходе которого система переходит из состояния в состояние, но вероятности состояний уже не меняются:
; .Коэффициент готовности kг.сможно рассчитать по системе (4.41) дифференциальных уравнений, приравнивая нулю их левые части dPi(t) / dt = 0, так как Pi= const при t ∞. Тогда система уравнений (4.41) превращается в систему алгебраических уравнений вида:
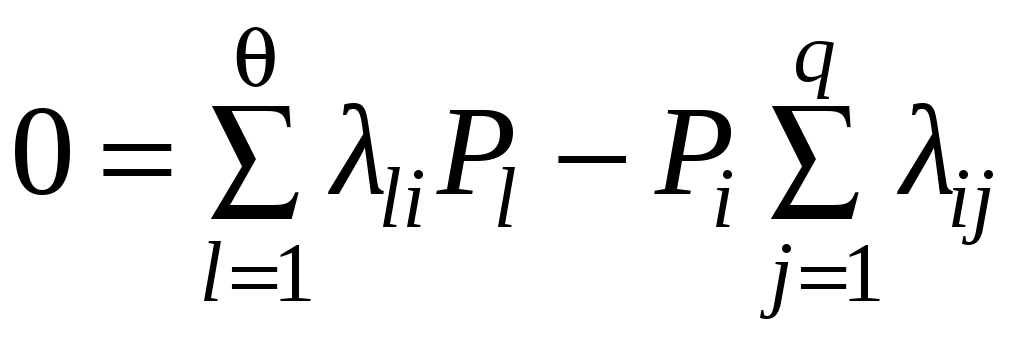, (4.44)и коэффициент готовности
(4.45)есть предельное значение функции готовности при установившемся режиме t→∞.
4. Параметр потока отказов системы:
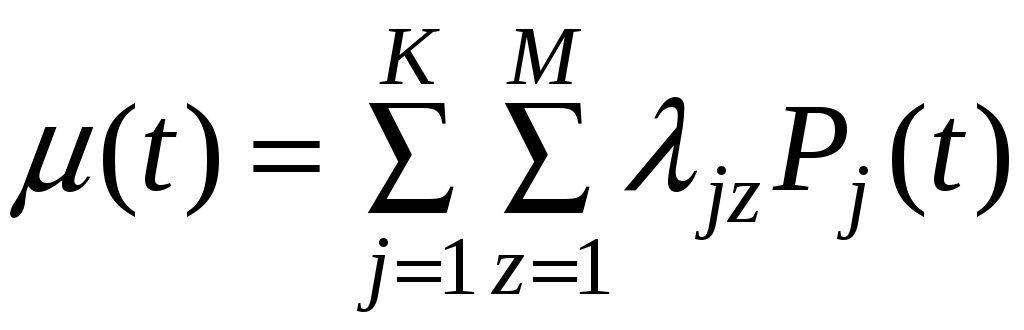, (4.46)где λjz – интенсивности (обобщенное обозначение) переходов из работоспособного состояния в неработоспособное.
5. Функция потока отказов:
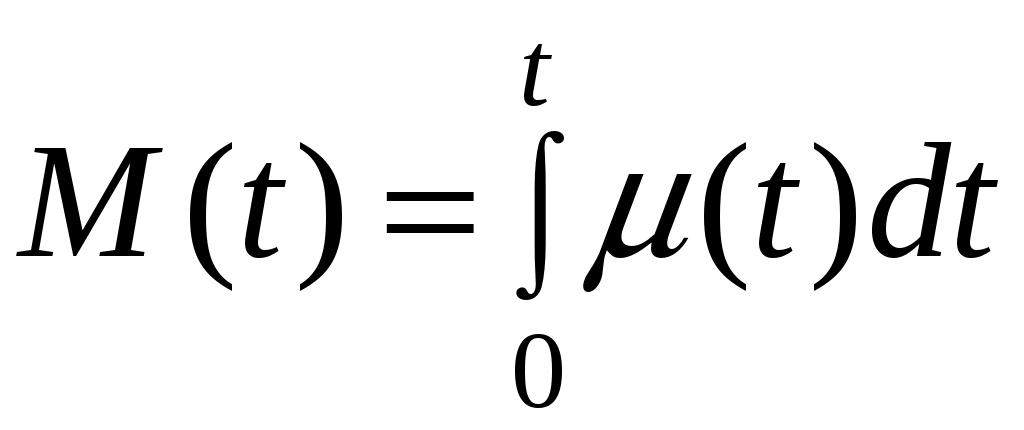. (4.47)6. Средняя наработка между отказами на интервале t:
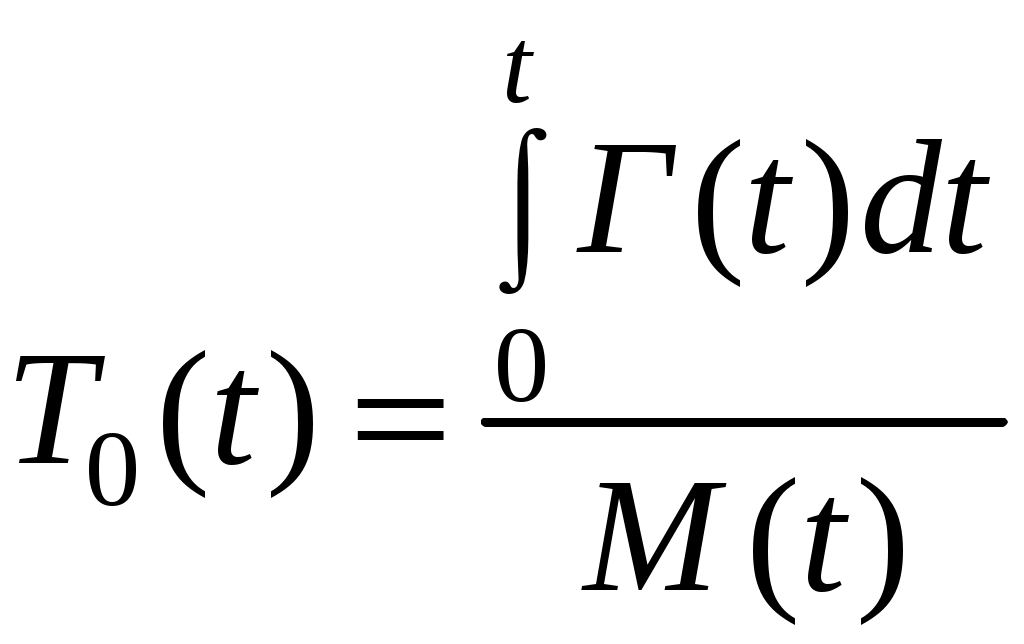. (4.48)Примечание: при t → ∞, когда Pj
(t = ∞) = Pj(∞) = Pj, средняя наработка между отказами T0= kг.с / μ, где µ(∞) = µ.
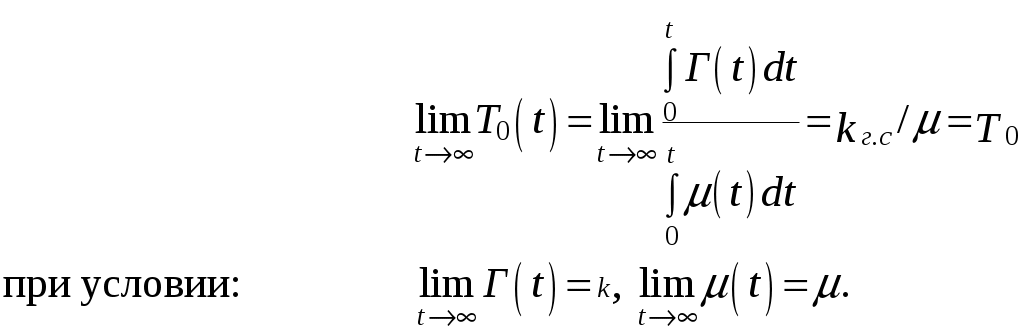
В качестве примера вычисления показателей надежности рассмотрен восстанавливаемый объект, у которого поток отказов простейший (пуассоновский) с параметром потока
μ = λ= 1/ T , (4.49)
а распределение времени восстановления подчиняется экспоненциальному распределению с интенсивностью восстановления
μ = 1/ TВ ,(4.50)
где T – средняя наработка между отказами; TВ – среднее время восстановления.
С
λ
остояния элемента: S0 – работоспособное; S1 – неработоспособное (рис. 4.16); Р0(t) – вероятность работоспособного состояния при t; P1(t) – вероятность неработоспособного состояния при t.
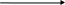
µ
λ
Рис. 4.16. Граф состояний восстанавливаемого объекта
Система дифференциальных уравнений:
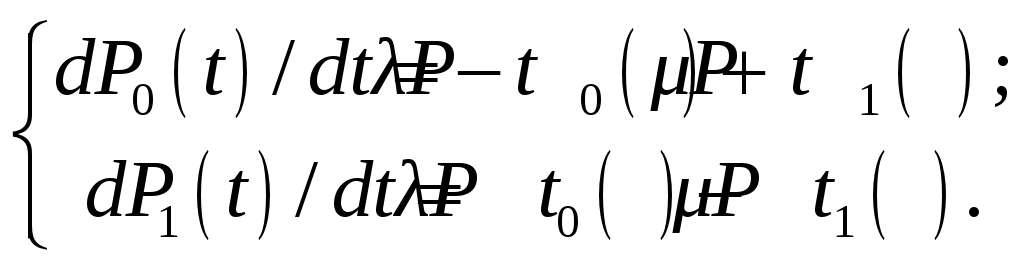(4.51)Начальные условия: при t = 0 P0(t = 0) = P0(0) = 1; P1(0) = 0.
Поскольку состояния S0и S1представляют полную группу событий, то
P0(t) + P1(t) = 1. (4.52)
Путём выражения P0(t) = 1 – P1(t) и подстановки в (4.51) получено одно дифференциальное уравнение относительно P1(t):
dP1(t)/dt = λ(1 – P1(t)) – μP1(t). (4.53)
Решение уравнения производится с использованием преобразования Лапласа. Преобразование Лапласа для вероятностей состояния
Pi(t):
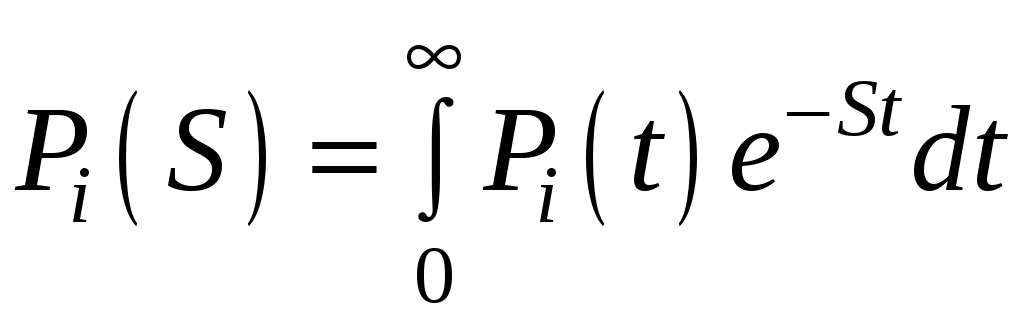,где Pi(S) = L{Pi(t)} – изображение вероятности Pi(t).
Преобразование Лапласа для производной dPi(t)/dt:
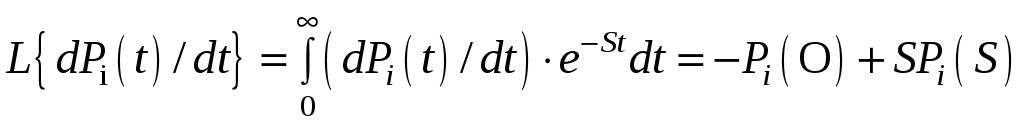.После применения преобразования Лапласа к левой и правой частям уравнения получено уравнение изображений:
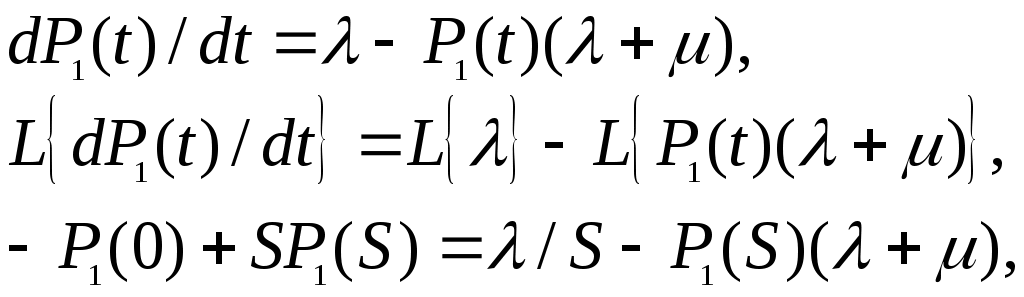
где L{λ} = λ L{1} = λ / S.
При P1(0) = 0
SP1(S) + P1(S)(λ + μ) = λ / S,
P1(S)(S + λ + μ) = λ / S.
Преобразованием приведенных соотношений получено выражение вероятности нахождения объекта в неработоспособном состоянии:
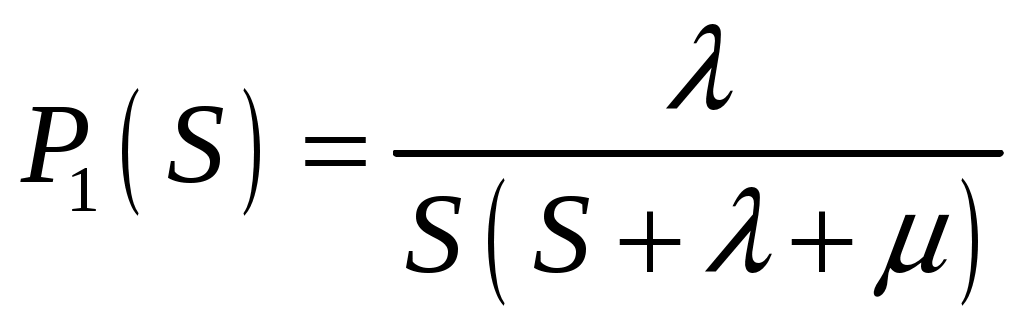. (4.54)Введение обозначения λ + μ = а позволяет преобразовать правую часть выражения (4.54):
.Применяя обратное преобразование Лапласа, с учётом L{f(t)} = 1/S,
а также f(t) = 1; L{f(t)} = 1/(S + a), получают f(t) = e–at, после чего находят вероятность пребывания объекта в неработоспособном состоянии в виде выражения:
. (4.55)Тогда вероятность нахождения в работоспособном состоянии
P0(t) = 1 – P1(t) равна:
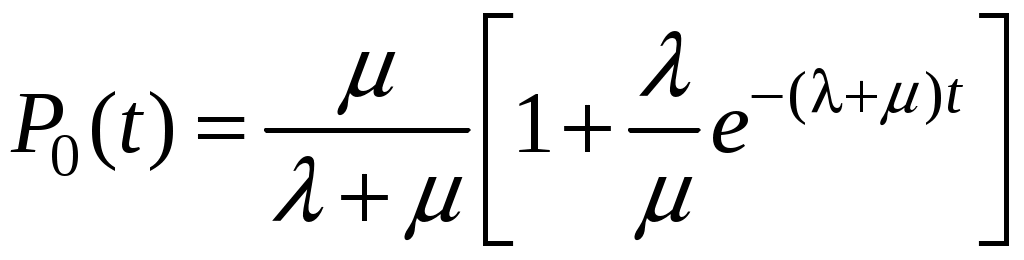. (4.56)С помощью полученных выражений можно рассчитать вероятность работоспособного состояния и отказа восстанавливаемого объекта в любой мо- мент t.
Коэффициент готовности системы kг.с определяется при установившемся режиме t ∞, при этом Pi(t) = Pi = const, поэтому составляется система алгебраических уравнений с нулевыми левыми частями, поскольку dPi(t)/dt = 0.
Так как kг.с есть вероятность того, что система окажется работоспособной в момент t при t ∞, то из полученной системы уравнений определяется
P0 = kг.
с .
При t ∞ алгебраические уравнения имеют вид:
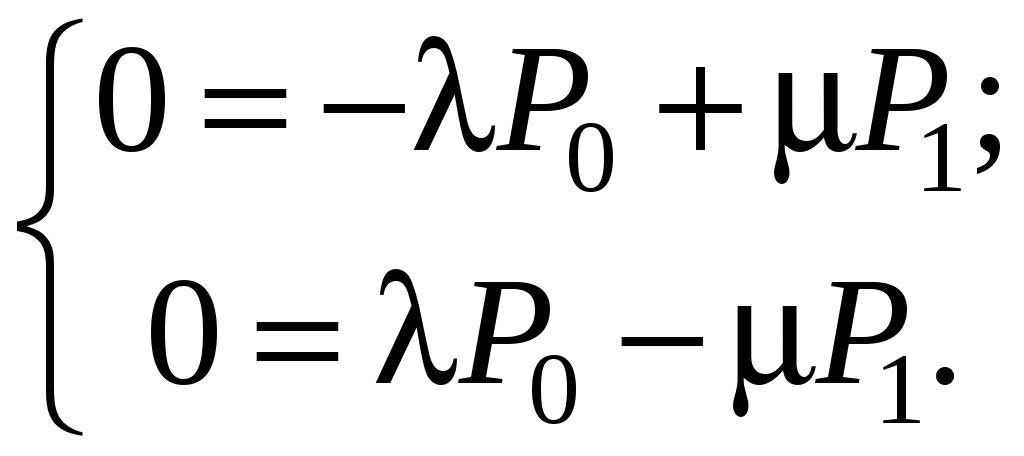(4.57)Дополнительное уравнение: P0+ P1 = 1.
При P1 = 1 – P0 получается 0 = λP0 – μ(1 – P0), или μ = P0(λ + μ),
откуда
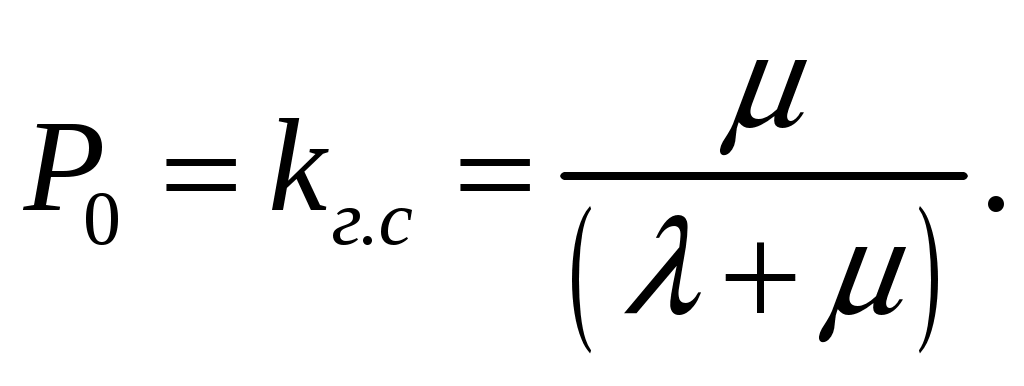(4.58)Остальные показатели надежности восстанавливаемого элемента:
– функция готовности Г(t) = P0(t);
– функция простоя П(t) = 1 – Г(t) = P1(t);
– параметр потока отказов µ(t) = λP0(t) = λГ(t),
при t ∞ (стационарный установившийся режим восстановления)
µ(t) = µ(∞) = µ = λP0 = λkг.с;
– ведущая функция потока отказов
– средняя наработка между отказами t0= kг.с / μ = kг.с /kг = 1/λ.
Метод дифференциальных уравнений может быть использован для расчёта показателей надёжности и невосстанавливаемых объектов (систем).
В этом случае неработоспособные состояния системы являются «поглощающими» и интенсивности λ выхода из этих состояний исключаются.
Для невосстанавливаемого объекта граф состояний имеет вид (рис. 4.17):
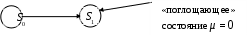
Рис. 4.17. Граф состояний невосстанавливаемого объекта
Система дифференциальных уравнений для данного объекта:
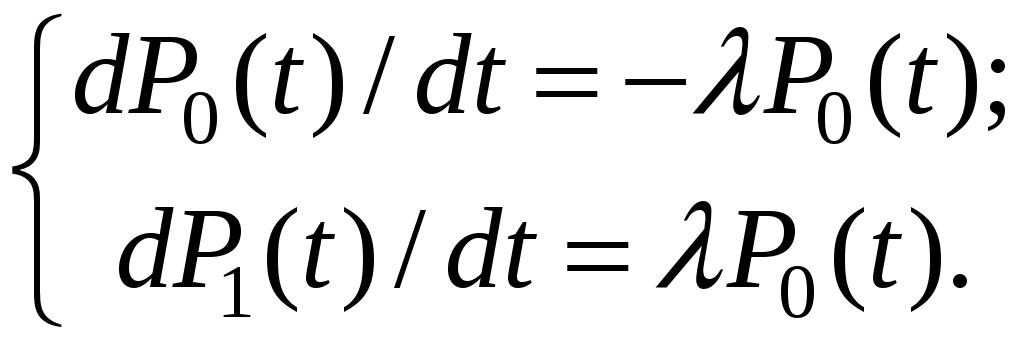
Начальные условия: P0 (0) = 1; P1(0) = 0.
Изображение по Лапласу первого уравнения системы:
; .После группировки:
; ,откуда
.
Используя обратное преобразование Лапласа, получают
.4.5.2. Связь логической схемы надёжности с графом состояний
Переход от логической схемы к графу состояний необходим:
– при смене методов расчёта надёжности и сравнении результатов;
– для оценки выигрыша в надёжности при переходе от невосстанавливаемой системы к восстанавливаемой.
Рассматриваются типовые логические структуры надежности. Для невосстанавливаемых систем граф – однонаправленный, переходы характеризуются интенсивностями отказов λ.
Для восстанавливаемых систем в графах состояний добавляются обратные стрелки, соответствующие интенсивностям восстановлений В (табл. 4.4).
Таблица 4.4
Типовые логические структуры надёжности
Структурная
логическая
схема
Графы состоний
Элементы различной надежности
Равнонадежные
элементы
Обозначения на графах состояний:
1 – работоспособное состояние элемента,
0 – неработоспособное состояние элемента.
Контрольные вопросы
1. В чём особенности марковского случайного процесса, на основе которого строится расчётная модель для восстанавливаемых объектов и систем?
2. Назовите основные этапы составления расчётной модели.
3. Поясните мнемоническое правило составления дифференциального уравнения вероятностей состояния (уравнение Колмогорова – Чепмена).
4. Дайте определение и поясните смысл показателей надежности восстанавливаемых объектов и систем.
5. Каковы особенности применения метода дифференциальных уравнений для расчета надежности невосстанавливаемых объектов?
6. На любом из примеров поясните связь графа состояний с логической структурой надёжности.
4.6. Пример расчёта безотказности
с использованием модели «прочность – нагрузка»
1. Рассчитать элемент, на который действует растягивающая нагрузка (рис. 4.18).
Принимается, что растягивающая нагрузка