ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 879
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
t = ∞. Это не является существенным недостатком, если T≥ 3S, так как площадь, очерченная уходящими в бесконечность ветвями кривой плотности, очень мала. Так, вероятность отказа за период времени до Т = –3S составляет всего 0,135 % и обычно не учитывается в расчетах. Наибольшая ордината кривой плотности распределения равна 0,399/S (рис. 4.6).
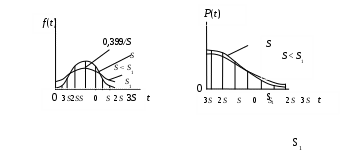
а) б)
Рис. 4.6. Функция плотности вероятности (а) и интегральная функция
вероятности нормального распределения (б)
Вероятность отказа при таком распределении определяется интегральной функцией
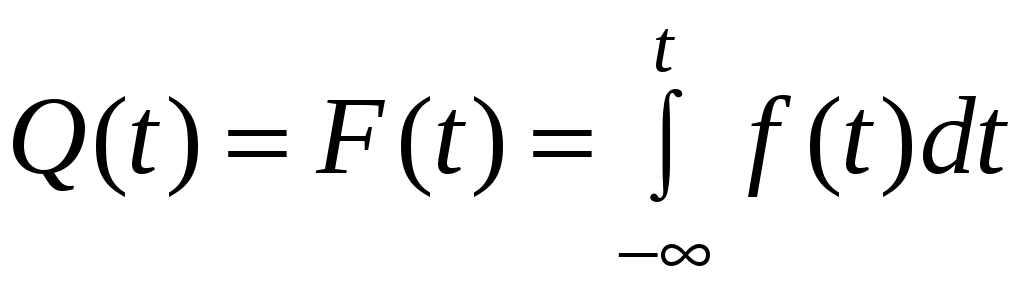. (4.13)
Вероятность безотказной работы
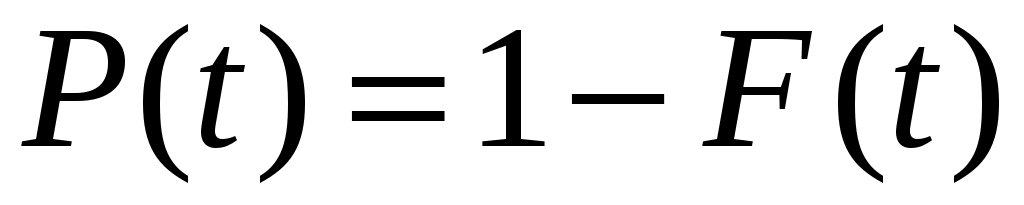, (4.14)
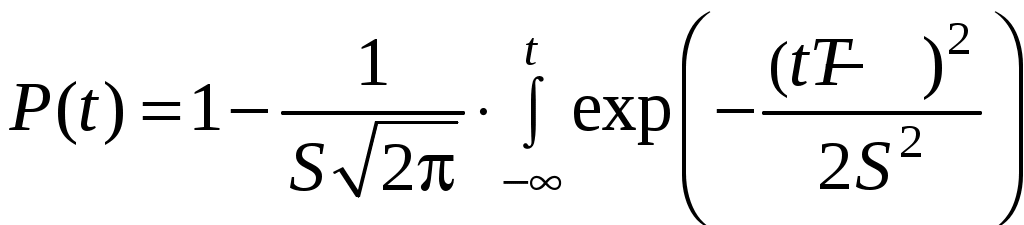. (4.15)
Вычисление интегралов заменяют использованием таблиц значений P(t) в зависимости от квантили нормированного нормального распределения
(табл. 4.2):
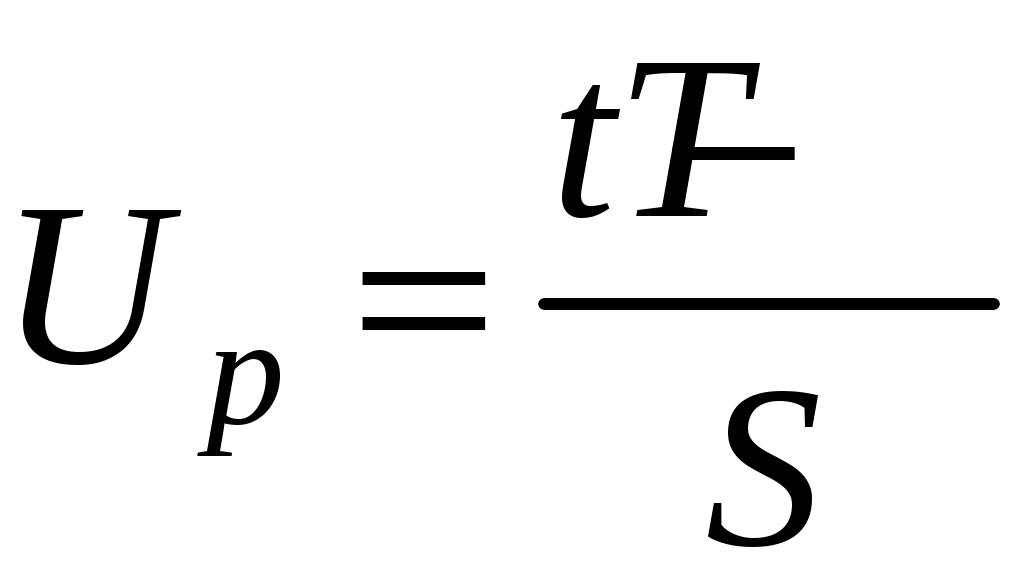. (4.16)
Помимо прямой задачи, т. е. оценки вероятности безотказной работы за данную наработку, зачастую требует решения обратное определение наработки, соответствующей заданной вероятности безотказной работы.
Значение этой наработки определяют также с помощью квантили:
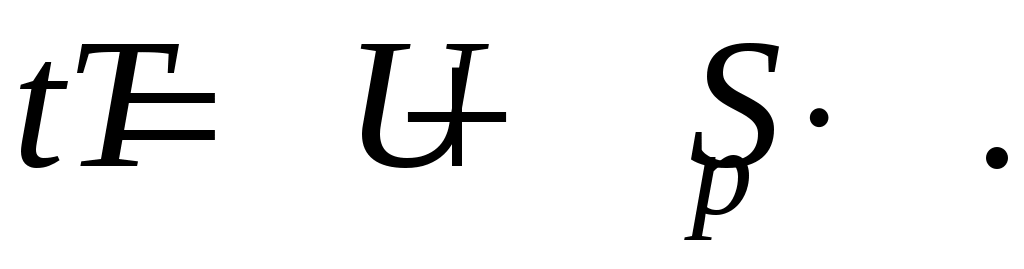(4.17)
Таблица 4.2
Нормальное распределение
Применение нормального закона ограничено, если мала вероятность отрицательных значений времени безотказной работы, заданная в виде:
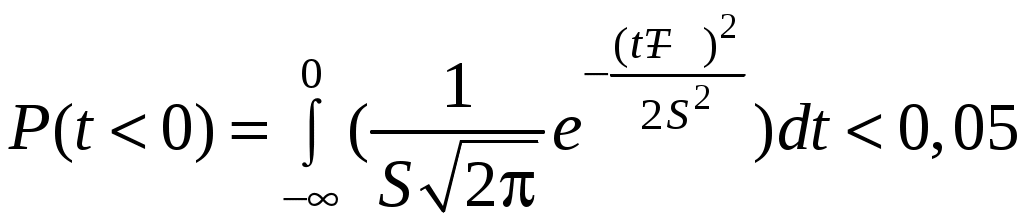. (4.18)
Если вероятность отрицательных значений времени безотказной работы оказывается достаточно большой величиной, то нормальное распределение для расчетов надёжности использовать нельзя. В этом случае переходят к логарифмически нормальному распределению вероятности безотказной работы.
При большем разбросе значений случайной величины T область возможных значений ограничивается слева (0, ∞) и используется усеченное нормальное распределение.
Все рассмотренные далее законы распределения наработки до отказа используются на практике для описания надёжности «стареющих» объектов, подверженных отказам вследствие износа.
4.3.2. Усеченное нормальное распределение
Усеченным нормальным распределением называется распределение, получаемое из классического нормального при ограничении интервала возможных значений наработки до отказа.
Известно, что корректность использования классического нормального распределения наработки достигается при Т ≥ 3S.
При малых значениях Т и большом S может возникать ситуация, когда функция f(t) «покрывает» своей левой ветвью область отрицательных наработок (рис. 4.7).
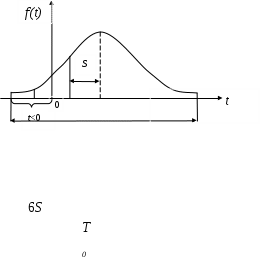
Рис. 4.7. Функция плотности вероятности усеченного нормального распределения
Таким образом, нормальное распределение, являясь общим случаем распределения случайной величины в диапазоне (–∞; +∞), лишь в частности (при определенных условиях) может быть использовано для моделей надёжности.
В общем случае усечение может быть:
левым – (0; +∞),
двусторонним – (t1, t2).
Для рассмотрения количественных характеристик надёжности при усеченном нормальном распределении вводится нормирующий множитель, чтобы сохранить условие нормирования плотности вероятности:
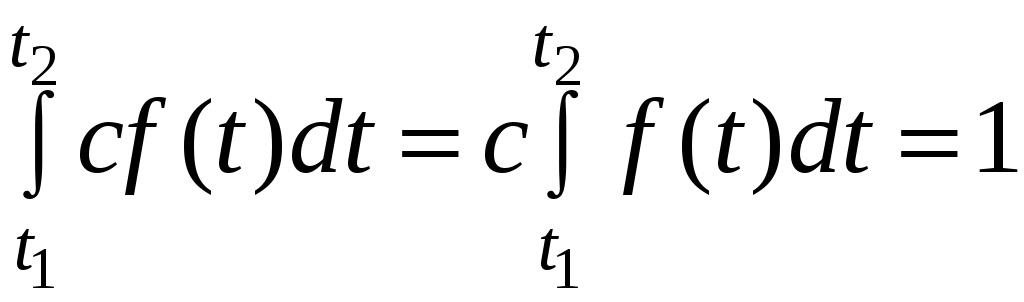, (4.19)
где
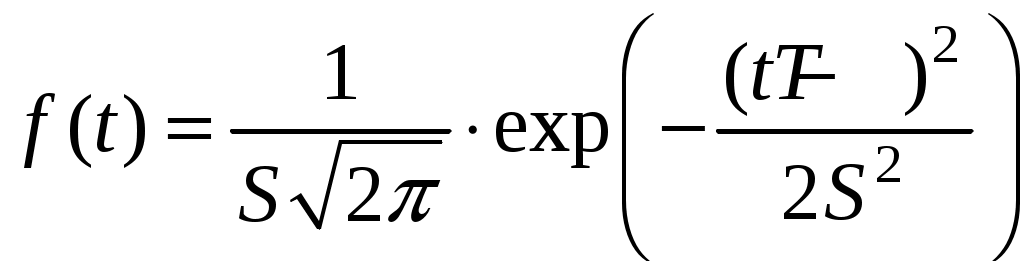, (4.20)
откуда
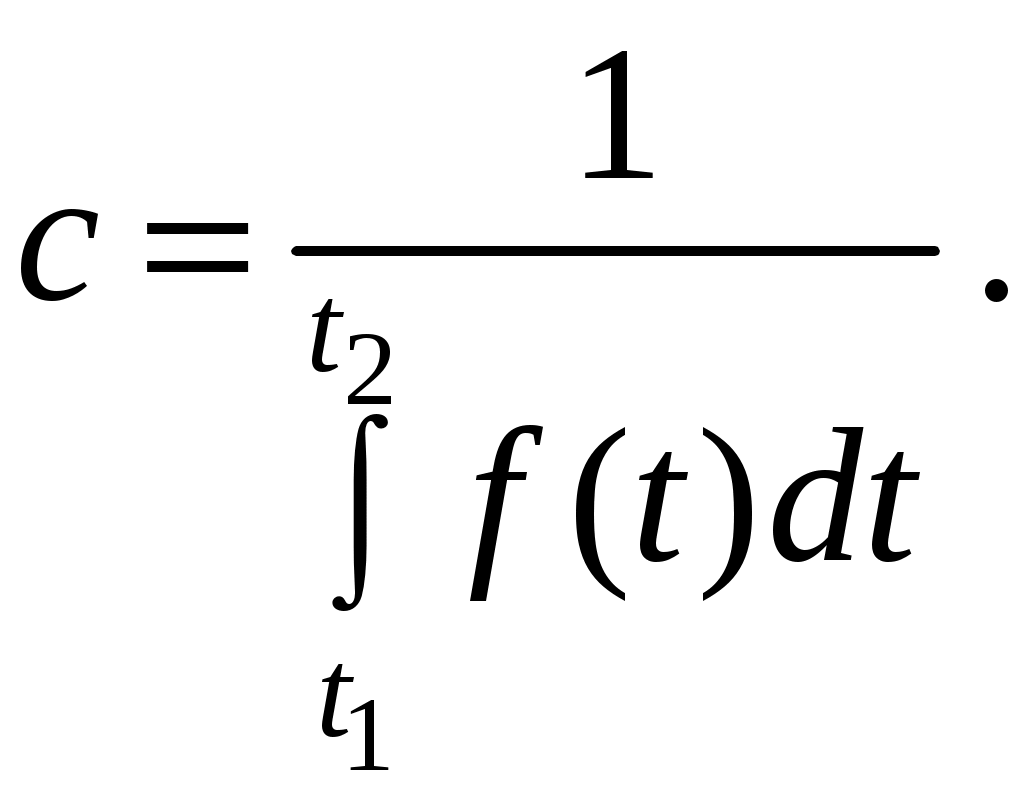
(4.21)
Переходя от случайной величины Т = {t} к величине X = {x}
x2 = (t2 –Т)/S,x1 = (t1 – Т)/S ,
получают
,
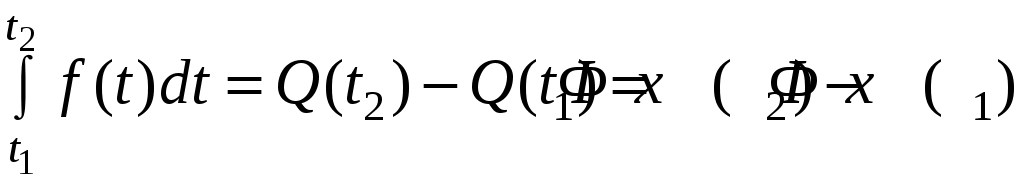откуда
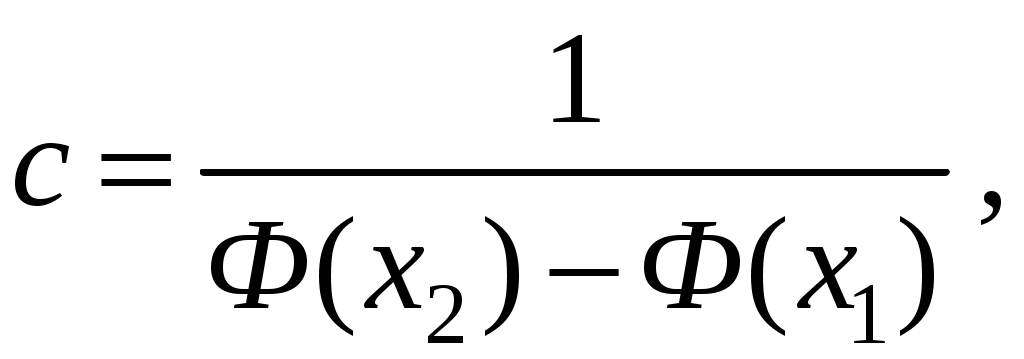(4.22)
где Ф(х) – интеграл Лапласа.
.
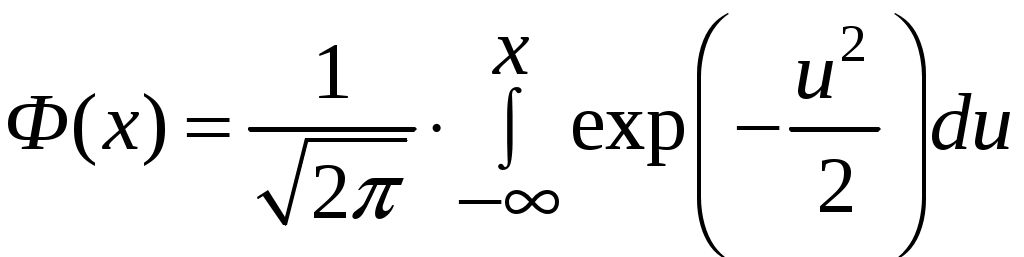Усеченный нормальный закон распределения применяется для описания постепенных отказов объектов, что характерно для «стареющих» объектов.
Поскольку [Ф(x2)–Ф(x1)] < 1, то c> 1, поэтому f1(t) > f2(t). Здесь f1(t) – функция плотности распределения отказов для нормального закона распределения, f2(t) – функция плотности распределения отказов для усеченного нормального закона распределения. Кривая f1(t) выше, чем f2(t), так как площади под кривыми f1(t) и f2(t) одинаковы и равны 1 (рис. 4.8):
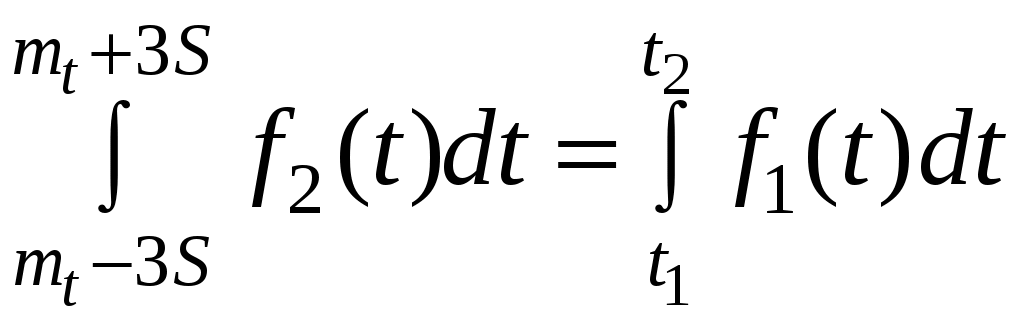(с погрешностью ≤ 1 %).
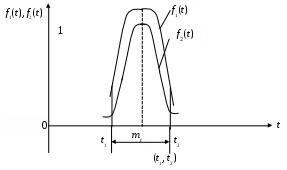
Рис. 4.8. Функция плотности распределения отказов
для нормального закона распределения f1(t) и функция плотности распределения отказов
для усеченного нормального закона распределения f2(t)
К
0
онтрольные вопросы
1. Почему распределение Гаусса называется нормальным?
2. Поясните влияние параметров распределения: математического ожидания и дисперсии по виду кривой плотности распределения отказов.
3. При каких условиях правильно использовать классическое нормальное распределение, а при каких – усечённое нормальное распределение?
4.3.3. Логарифмически нормальное распределение
При логарифмически нормальном распределении нормально распределенным является логарифм (lg t) случайной величины Т, а не сама эта величина.
Это распределение обеспечивает более точное, чем нормальное распределение, описание наработки до отказа тех объектов, у которых отказ возникает вследствие усталости, например подшипников качения, электронных ламп и пр.
Оно используется при обработке опытных данных об усталостной долговечности металлов, времени безотказной работы некоторых объектов.
Логарифмически нормальное распределение позволяет описывать течение времени безотказной работы объектов, имеющих свойство «упрочняться» по ходу времени эксплуатации. «Упрочнение» проявляется в постепенном уменьшении скорости износа.
Плотность распределения выражается зависимостью
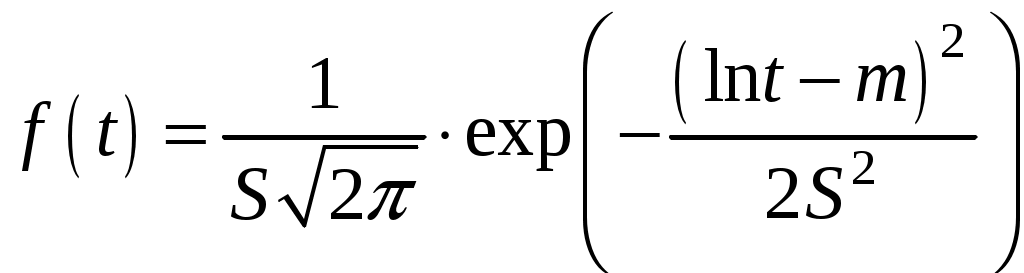. (4.23)
Параметры m и S по результатам N испытаний принимаются:
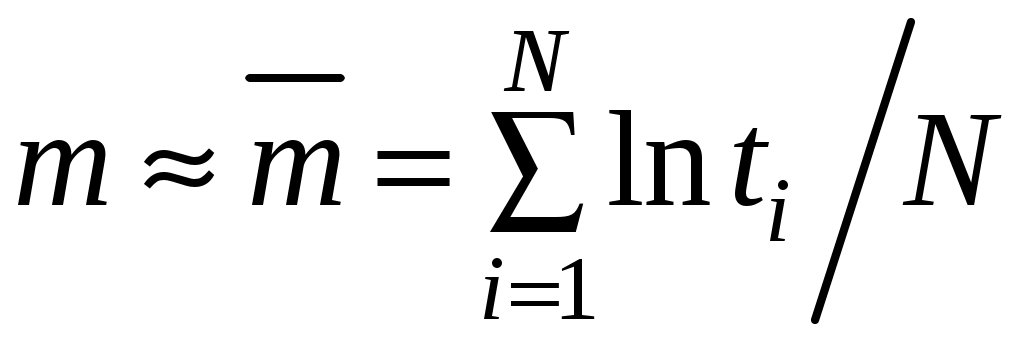, (4.24)
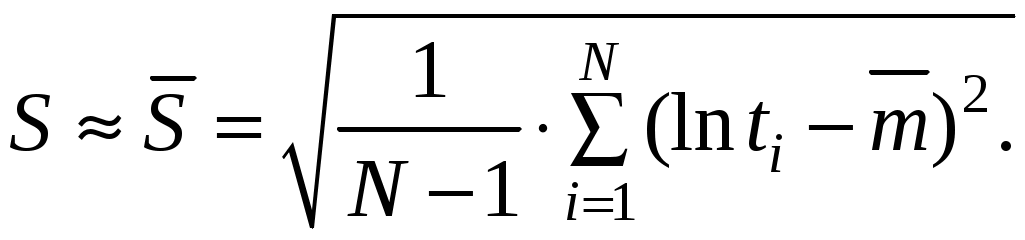(4.25)
Вероятность безотказной работы можно определить по таблице нормального распределения (см. табл. 4.2) в зависимости от значения квантили:
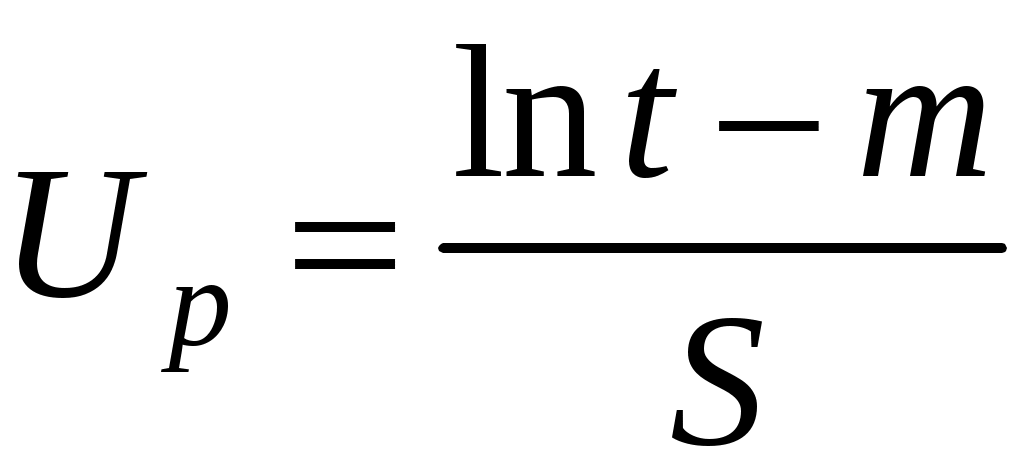. (4.26)
Математическое ожидание наработки до отказа:
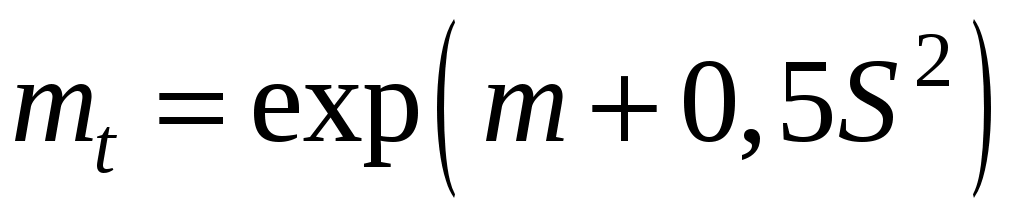. (4.27)
Среднее квадратическое отклонение
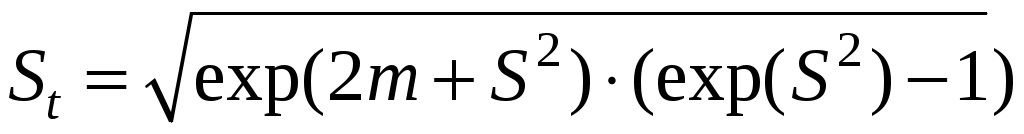. (4.28)
Графики изменения показателей надежности при логарифмически нормальном распределении приведены на рис. 4.9.
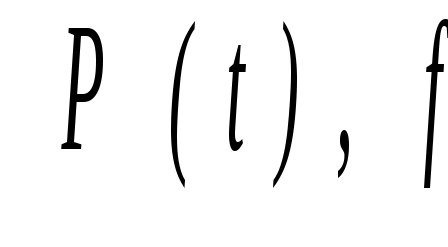
Рис. 4.9. Графики функций показателей безотказности
при логарифмически нормальном распределении
4.3.4. Гамма-распределение
Гамма-распределение времени безотказной работы описывает схему непрерывного, постепенного износа, при котором отказ не наступает вследствие первого же повреждения, а является следствием накопления повреждений. Каждое из этих повреждений происходит по схеме мгновенного повреждения.
Граничными условиями применения гамма-распределения являются следующие:
– средняя скорость износа устройства постоянна;
– средняя скорость износа подвержена случайным вариациям;
– начальное качество исследуемых устройств полностью однородно.
Случайная величина наработки до отказа Tимеет гамма-распределение с параметрами α(масштабный параметр) и β(параметр формы), где
,
>
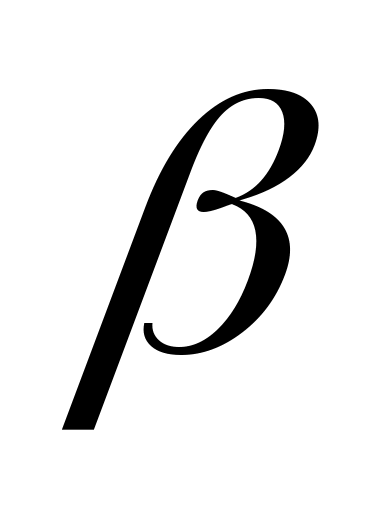0, причём
– целое число, если функция плотности распределения описывается выражением:
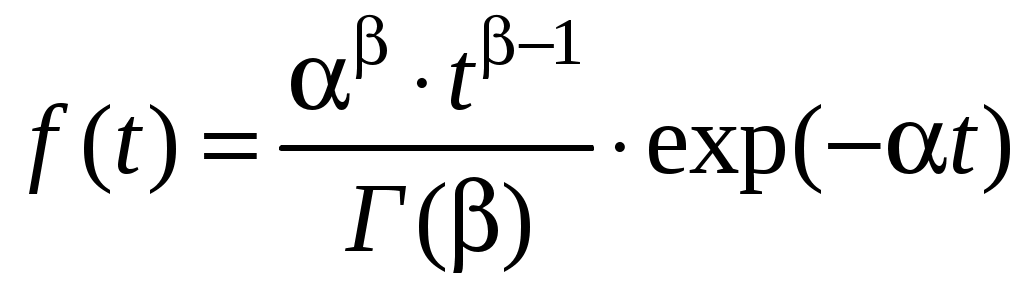, (4.29)
где Г(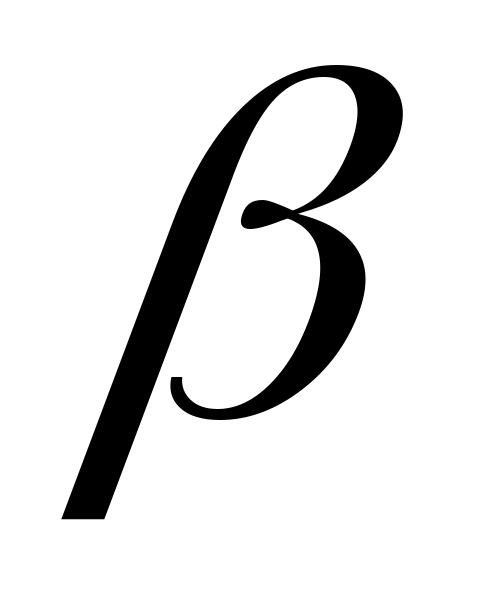
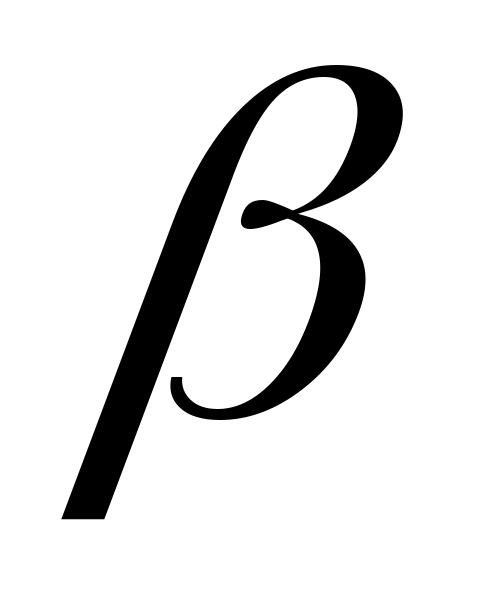) = ( – 1)! – гамма-функция Эйлера.
Очевидно, что при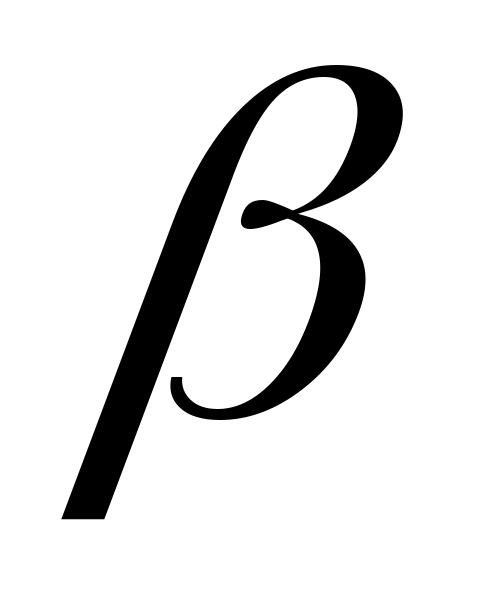 = 1 выражение (4.29) упрощается до вида 
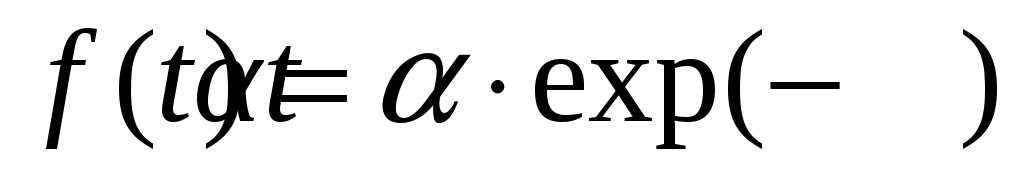, соответствующего экспоненциальному распределению.
Гамма-распределение наиболее хорошо описывает распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону.
При больших значениях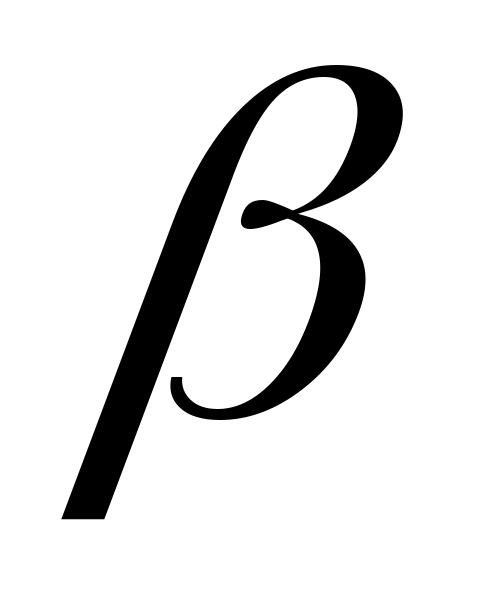 гамма-распределение сходится к нормальному распределению с параметрами: 
, 
.
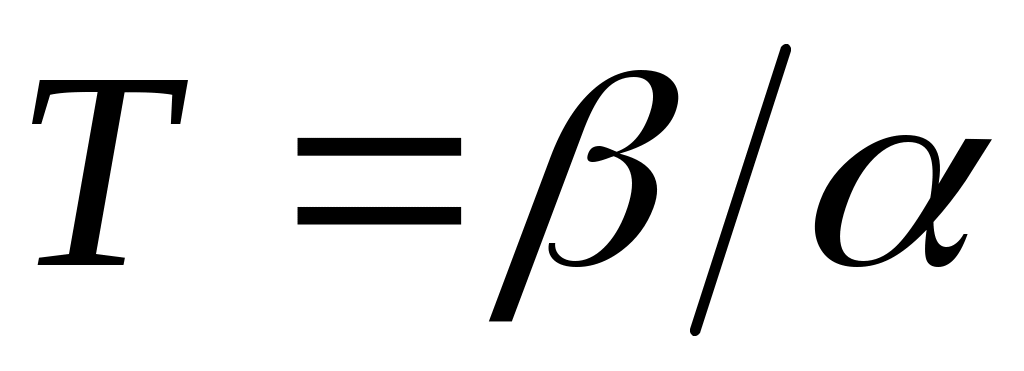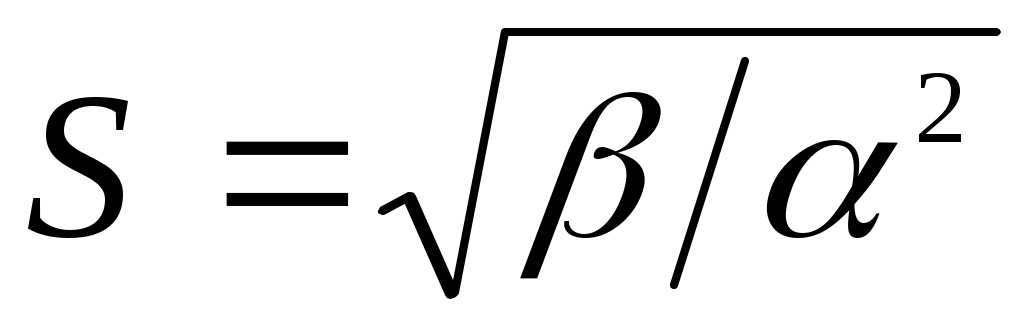Графики изменения показателей надежности при гамма-распределении приведены на рис. 4.10.
Числовые характеристики наработки до отказа:
– средняя наработка (математическое ожидание наработки) до отказа
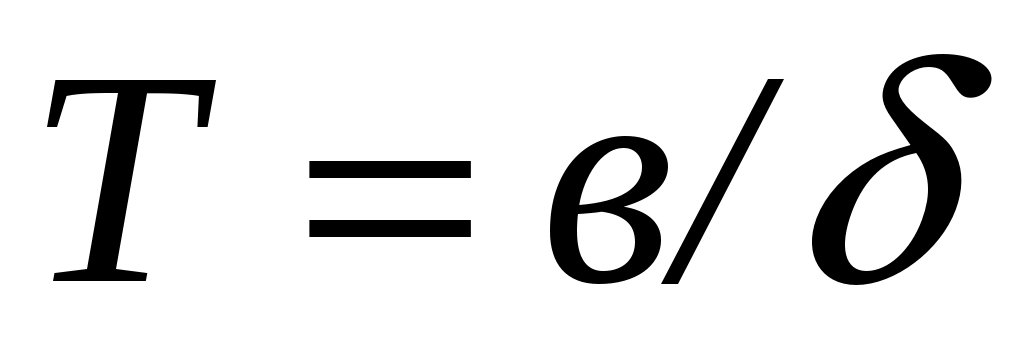,(4.30)
– дисперсия наработки до отказа
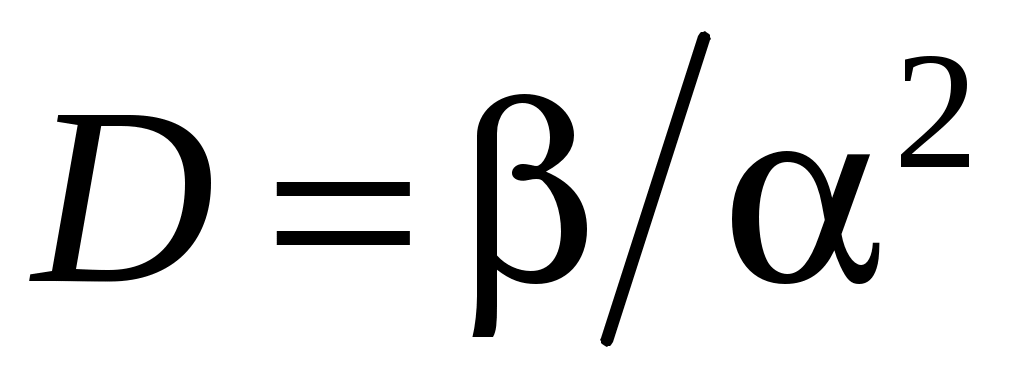. (4.31)
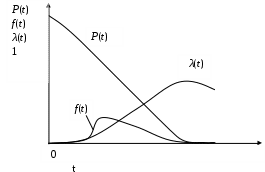
Рис. 4.10. Графики изменения показателей надежности при гамма-распределении
4.3.5. Распределение Вейбулла – Гнеденко
Распределение Вейбулла – Гнеденко довольно универсально, охватывает путем варьирования параметров широкий диапазон случаев изменения вероятностей. Наряду с логарифмическим нормальным распределением оно удовлетворительно описывает наработку деталей по усталостным разрушениям, наработку до отказа подшипников, радиодеталей. Используется для оценки надежности деталей и узлов машин, в частности автомобилей, подъемно-транспортных и других машин. Применяется также для оценки надежности по приработочным отказам.
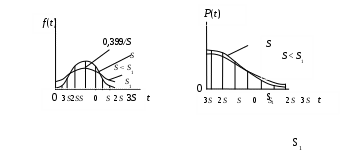
а) б)
Рис. 4.6. Функция плотности вероятности (а) и интегральная функция
вероятности нормального распределения (б)
Вероятность отказа при таком распределении определяется интегральной функцией
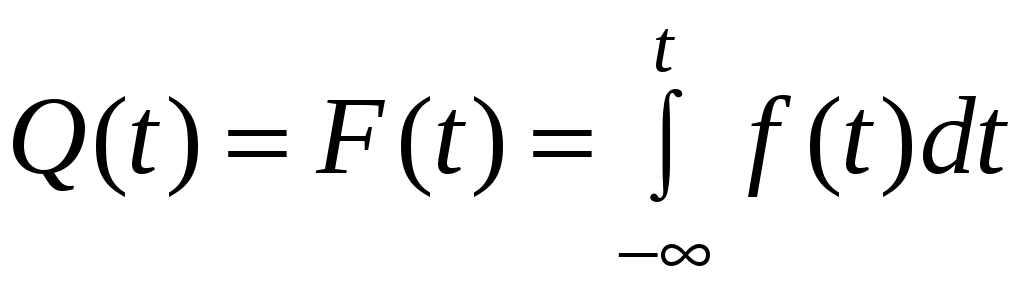. (4.13)Вероятность безотказной работы
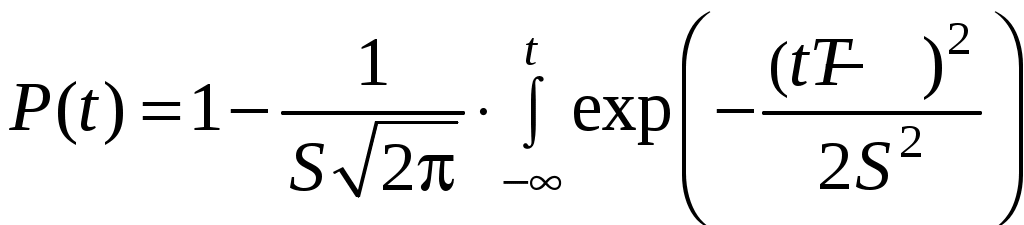, (4.14) . (4.15)Вычисление интегралов заменяют использованием таблиц значений P(t) в зависимости от квантили нормированного нормального распределения
(табл. 4.2):
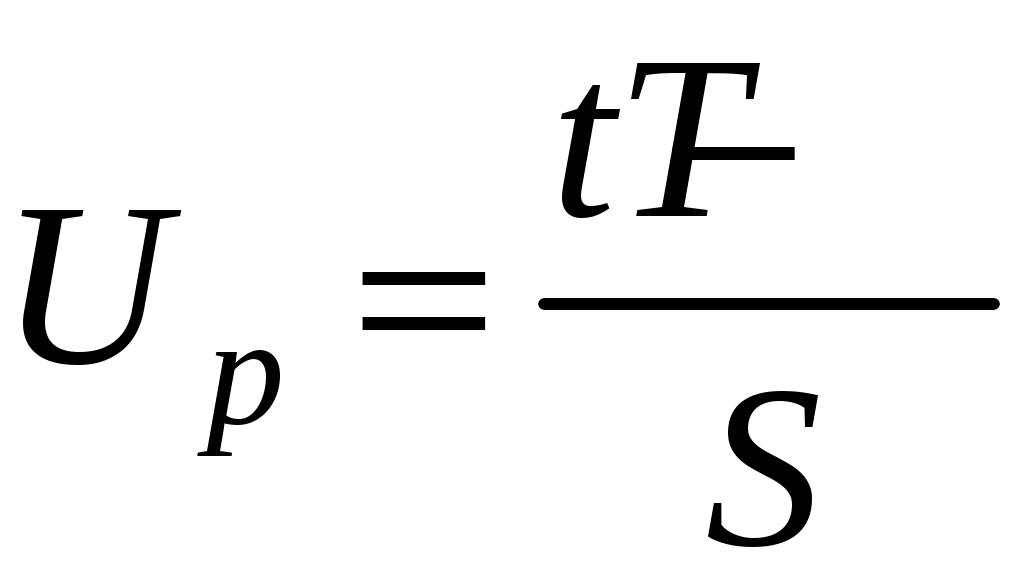. (4.16)Помимо прямой задачи, т. е. оценки вероятности безотказной работы за данную наработку, зачастую требует решения обратное определение наработки, соответствующей заданной вероятности безотказной работы.
Значение этой наработки определяют также с помощью квантили:
(4.17)Таблица 4.2
Нормальное распределение
| Квантиль Up | Вероятность безотказной работы P(t) | Квантиль Up | Вероятность безотказной работы P(t) |
| 0,0 | 0,5000 | –1,282 | 0,9000 |
| –0,1 | 0,5398 | –1,400 | 0,9192 |
| –0,2 | 0,5793 | –1,600 | 0,9452 |
| –0,3 | 0,6179 | –1,800 | 0,9641 |
| –0,4 | 0,6552 | –2,000 | 0,9772 |
| –0,5 | 0,6915 | –2,200 | 0,9861 |
| –0,6 | 0,7257 | –2,236 | 0,9900 |
| –0,7 | 0,7580 | –2,500 | 0,9938 |
| –0,8 | 0,7881 | –3,090 | 0,9990 |
| –0,9 | 0,8159 | –3,500 | 0,9998 |
| –1,0 | 0,8413 | –3,719 | 0,9999 |
Применение нормального закона ограничено, если мала вероятность отрицательных значений времени безотказной работы, заданная в виде:
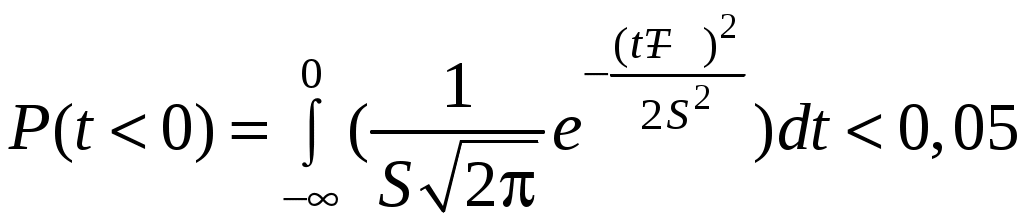. (4.18)Если вероятность отрицательных значений времени безотказной работы оказывается достаточно большой величиной, то нормальное распределение для расчетов надёжности использовать нельзя. В этом случае переходят к логарифмически нормальному распределению вероятности безотказной работы.
При большем разбросе значений случайной величины T область возможных значений ограничивается слева (0, ∞) и используется усеченное нормальное распределение.
Все рассмотренные далее законы распределения наработки до отказа используются на практике для описания надёжности «стареющих» объектов, подверженных отказам вследствие износа.
4.3.2. Усеченное нормальное распределение
Усеченным нормальным распределением называется распределение, получаемое из классического нормального при ограничении интервала возможных значений наработки до отказа.
Известно, что корректность использования классического нормального распределения наработки достигается при Т ≥ 3S.
При малых значениях Т и большом S может возникать ситуация, когда функция f(t) «покрывает» своей левой ветвью область отрицательных наработок (рис. 4.7).
Рис. 4.7. Функция плотности вероятности усеченного нормального распределения
Таким образом, нормальное распределение, являясь общим случаем распределения случайной величины в диапазоне (–∞; +∞), лишь в частности (при определенных условиях) может быть использовано для моделей надёжности.
В общем случае усечение может быть:
левым – (0; +∞),
двусторонним – (t1, t2).
Для рассмотрения количественных характеристик надёжности при усеченном нормальном распределении вводится нормирующий множитель, чтобы сохранить условие нормирования плотности вероятности:
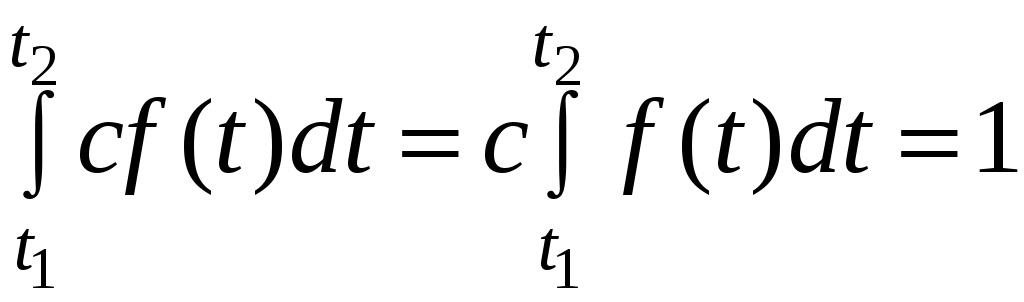, (4.19)где
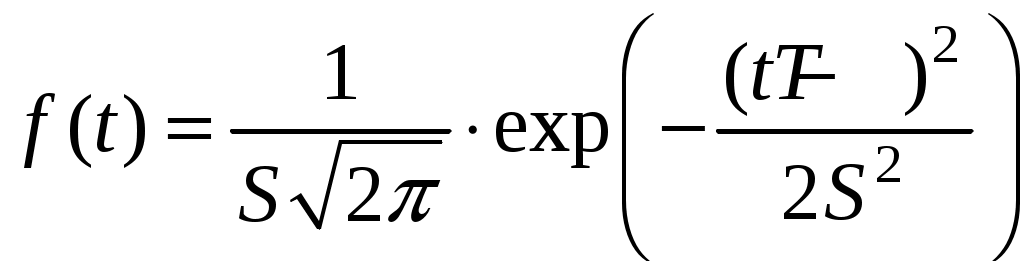, (4.20)откуда
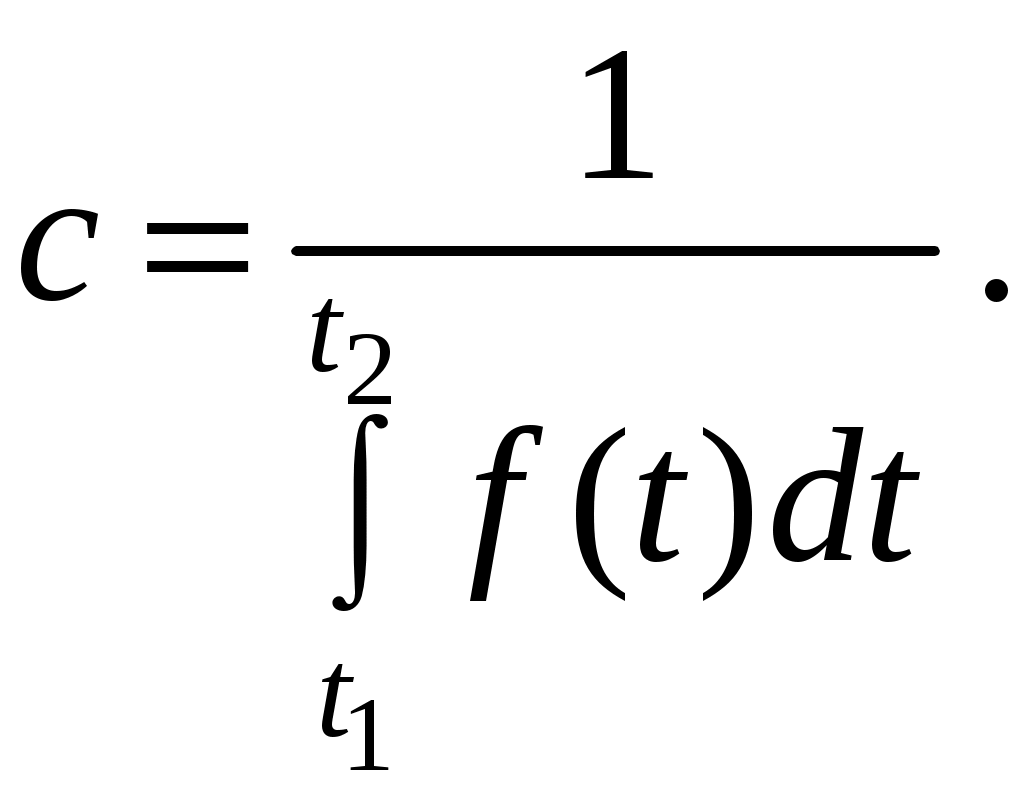
(4.21)
Переходя от случайной величины Т = {t} к величине X = {x}
x2 = (t2 –Т)/S,x1 = (t1 – Т)/S ,
получают
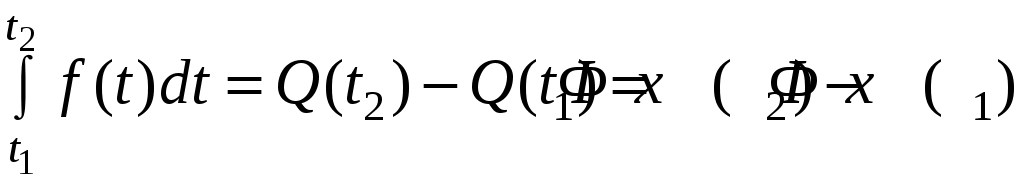,откуда
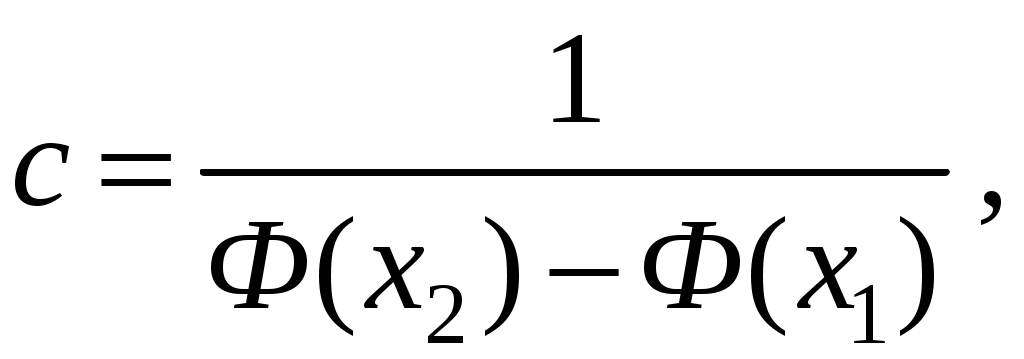(4.22)где Ф(х) – интеграл Лапласа.
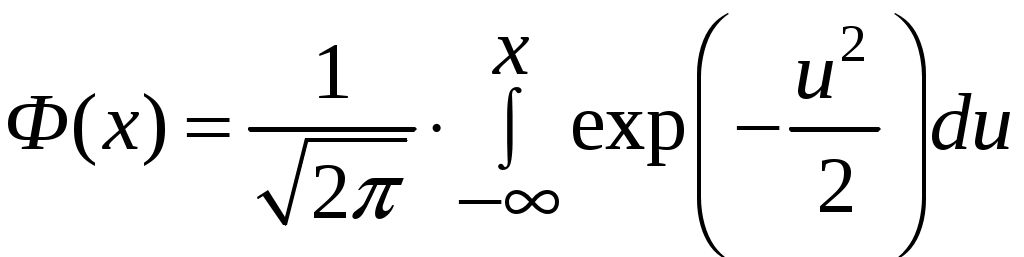.Усеченный нормальный закон распределения применяется для описания постепенных отказов объектов, что характерно для «стареющих» объектов.
Поскольку [Ф(x2)–Ф(x1)] < 1, то c> 1, поэтому f1(t) > f2(t). Здесь f1(t) – функция плотности распределения отказов для нормального закона распределения, f2(t) – функция плотности распределения отказов для усеченного нормального закона распределения. Кривая f1(t) выше, чем f2(t), так как площади под кривыми f1(t) и f2(t) одинаковы и равны 1 (рис. 4.8):
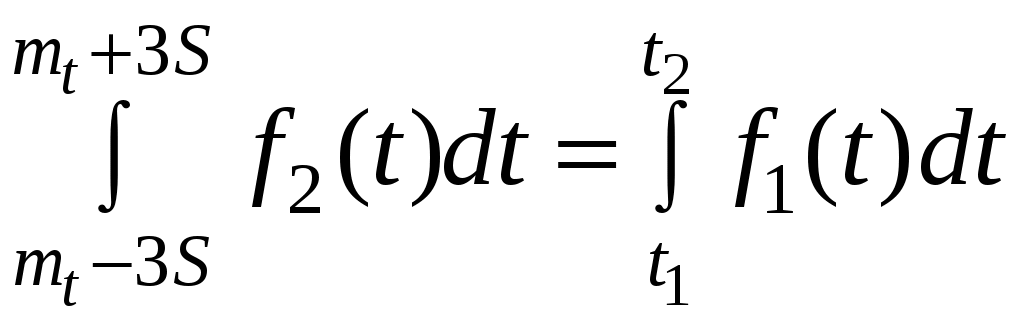(с погрешностью ≤ 1 %). Рис. 4.8. Функция плотности распределения отказов
для нормального закона распределения f1(t) и функция плотности распределения отказов
для усеченного нормального закона распределения f2(t)
К
0
онтрольные вопросы
1. Почему распределение Гаусса называется нормальным?
2. Поясните влияние параметров распределения: математического ожидания и дисперсии по виду кривой плотности распределения отказов.
3. При каких условиях правильно использовать классическое нормальное распределение, а при каких – усечённое нормальное распределение?
4.3.3. Логарифмически нормальное распределение
При логарифмически нормальном распределении нормально распределенным является логарифм (lg t) случайной величины Т, а не сама эта величина.
Это распределение обеспечивает более точное, чем нормальное распределение, описание наработки до отказа тех объектов, у которых отказ возникает вследствие усталости, например подшипников качения, электронных ламп и пр.
Оно используется при обработке опытных данных об усталостной долговечности металлов, времени безотказной работы некоторых объектов.
Логарифмически нормальное распределение позволяет описывать течение времени безотказной работы объектов, имеющих свойство «упрочняться» по ходу времени эксплуатации. «Упрочнение» проявляется в постепенном уменьшении скорости износа.
Плотность распределения выражается зависимостью
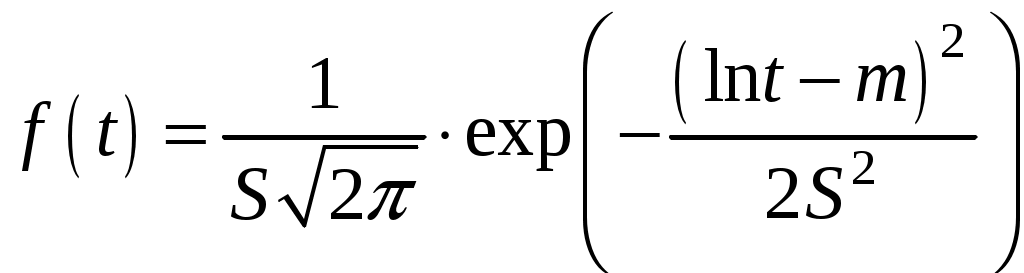. (4.23)Параметры m и S по результатам N испытаний принимаются:
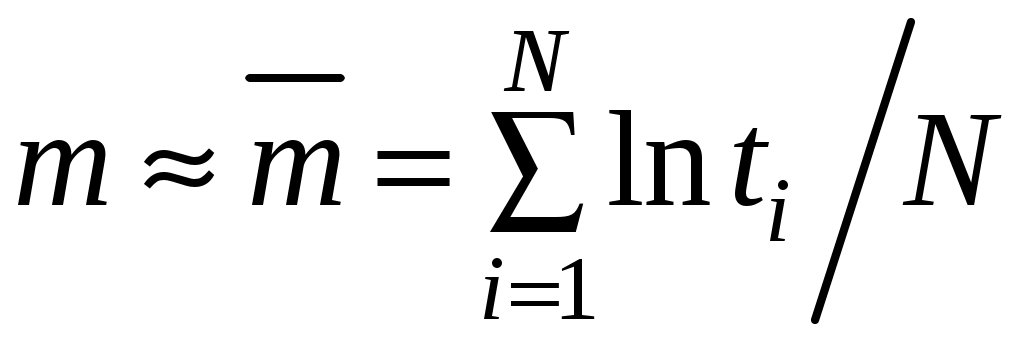, (4.24) 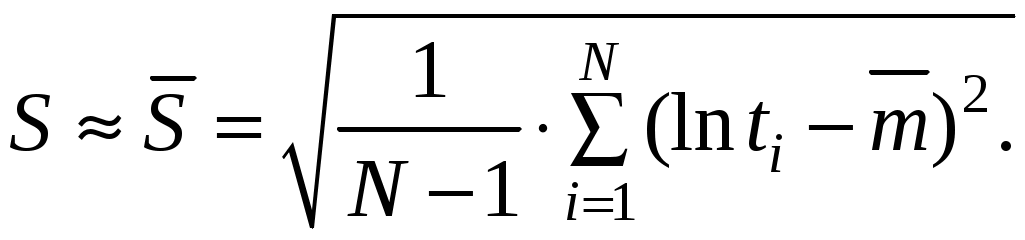(4.25)Вероятность безотказной работы можно определить по таблице нормального распределения (см. табл. 4.2) в зависимости от значения квантили:
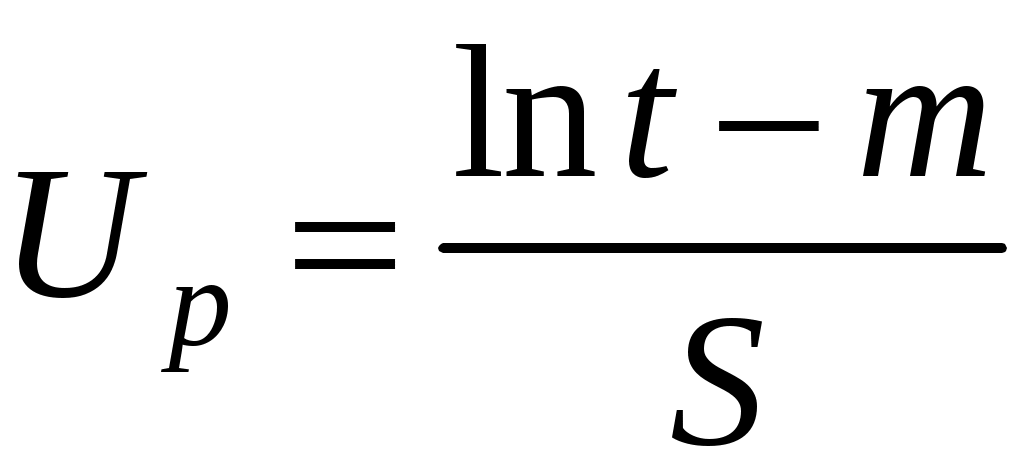. (4.26)Математическое ожидание наработки до отказа:
. (4.27)Среднее квадратическое отклонение
. (4.28)Графики изменения показателей надежности при логарифмически нормальном распределении приведены на рис. 4.9.
Рис. 4.9. Графики функций показателей безотказности
при логарифмически нормальном распределении
4.3.4. Гамма-распределение
Гамма-распределение времени безотказной работы описывает схему непрерывного, постепенного износа, при котором отказ не наступает вследствие первого же повреждения, а является следствием накопления повреждений. Каждое из этих повреждений происходит по схеме мгновенного повреждения.
Граничными условиями применения гамма-распределения являются следующие:
– средняя скорость износа устройства постоянна;
– средняя скорость износа подвержена случайным вариациям;
– начальное качество исследуемых устройств полностью однородно.
Случайная величина наработки до отказа Tимеет гамма-распределение с параметрами α(масштабный параметр) и β(параметр формы), где
, >
0, причём
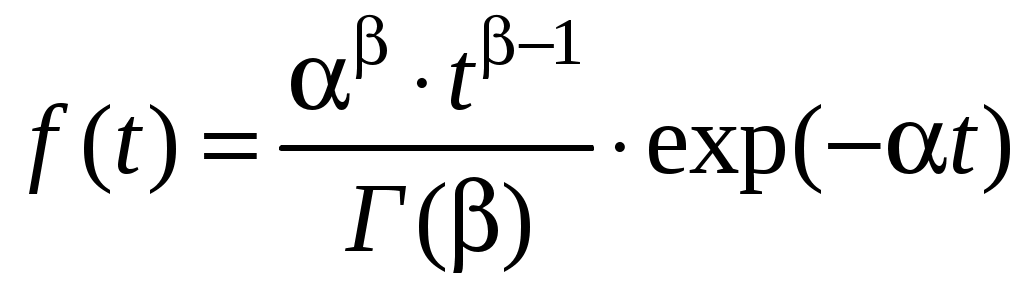– целое число, если функция плотности распределения описывается выражением: , (4.29)где Г(
) = ( – 1)! – гамма-функция Эйлера. Очевидно, что при
= 1 выражение (4.29) упрощается до вида , соответствующего экспоненциальному распределению.Гамма-распределение наиболее хорошо описывает распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону.
При больших значениях
гамма-распределение сходится к нормальному распределению с параметрами: , .Графики изменения показателей надежности при гамма-распределении приведены на рис. 4.10.
Числовые характеристики наработки до отказа:
– средняя наработка (математическое ожидание наработки) до отказа
,(4.30)– дисперсия наработки до отказа
. (4.31) Рис. 4.10. Графики изменения показателей надежности при гамма-распределении
4.3.5. Распределение Вейбулла – Гнеденко
Распределение Вейбулла – Гнеденко довольно универсально, охватывает путем варьирования параметров широкий диапазон случаев изменения вероятностей. Наряду с логарифмическим нормальным распределением оно удовлетворительно описывает наработку деталей по усталостным разрушениям, наработку до отказа подшипников, радиодеталей. Используется для оценки надежности деталей и узлов машин, в частности автомобилей, подъемно-транспортных и других машин. Применяется также для оценки надежности по приработочным отказам.