Файл: Учебное пособие в двух частях Часть Основы теории.doc

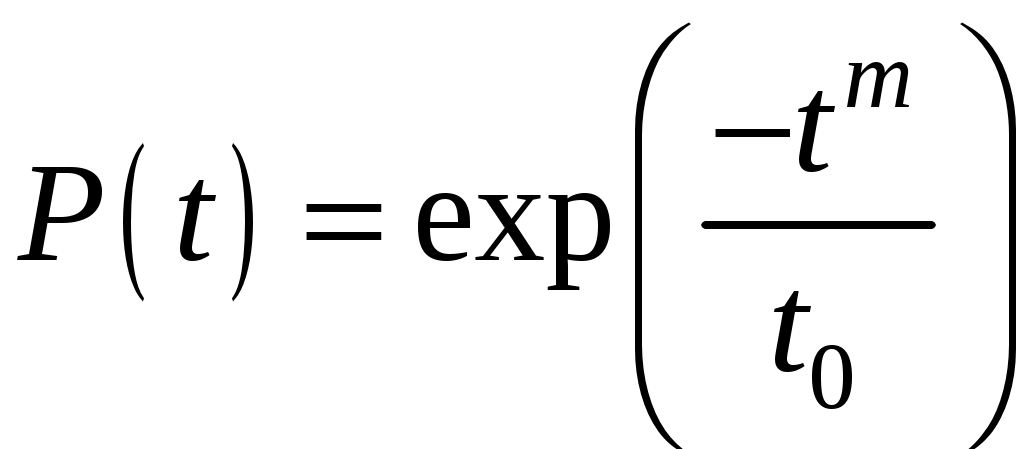. (4.32)

(Здесь t₀– значение времени, при котором плотность вероятности максимальна, в теории вероятностей носит название мода).

Интенсивность отказов

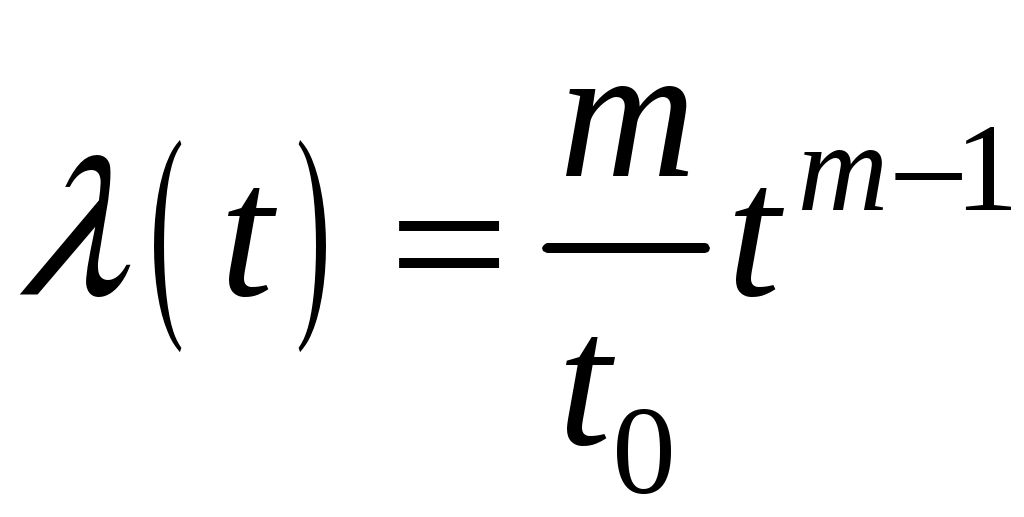. (4.33)

Плотность распределения

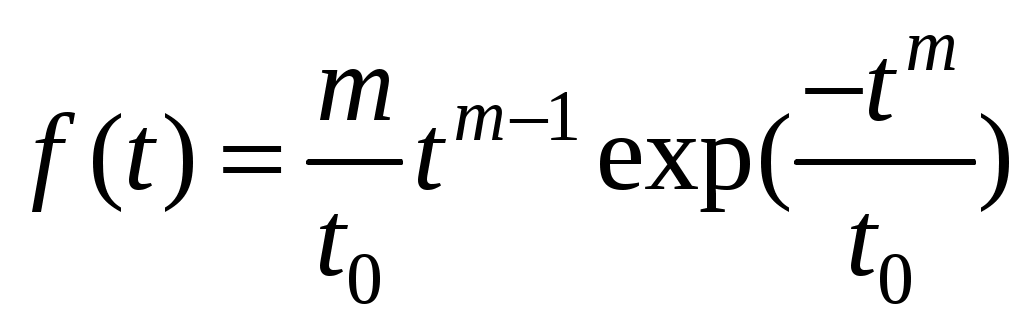. (4.34)

Из формул (4.33) и (4.34) видно, что распределение Вейбулла – Гнеденко имеет два параметра: параметр формы m >1 и параметр масштаба t₀.

Математическое ожидание и среднее квадратическое отклонение рассчитываются соответственно по формулам:

, (4.35)

, (4.36)

где b_m и с_m – коэффициенты, выбираемые по табл. 4.3.
Таблица 4.3

_{Коэффициенты для расчёта параметров mt и st}

Параметр формы m	1/m	b_m	с_m	Коэффициент вариации
0,400	2,5	3,32	10,4	3,14
0,455	2,2	2,42	6,22	2,57
0,500	2,0	2,00	4,47	2,24
0,556	1,8	1,68	3,26	1,94
0,625	1,6	1,43	2,39	1,67
0,833	1,2	1,10	1,33	1,21
1,2	0,833	0,941	0,787	0,837
1,6	0,625	0,897	0,574	0,640
2,0	0,500	0,887	0,463	0,523
2,5	0,400	0,886	0,380	0,428

Возможность и универсальность распределения Вейбулла – Гнеденко видны из следующих пояснений (рис. 4.11).

а)

б)

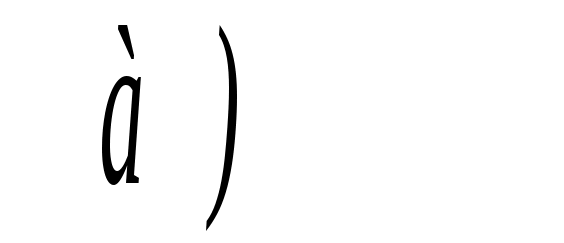
Рис. 4.11. Основные характеристики распределения Вейбулла – Гнеденко при разных
параметрах m: а – плотность вероятности f(t); б – интенсивность отказов λ(t)
При m< 1 функции λ(t) и f(t) наработки до отказа убывающие.

При m = 1 распределение превращается в экспоненциальное, λ(t) = const
и f(t) – убывающая функция.

При m > 1 функция f(t) – одновершинная, функция λ(t) непрерывно возрастающая, при 1 < m < 2 – с выпуклостью вверх, а при m > 2 – с выпуклостью вниз.

При m = 2 функция λ(t) является линейной и распределение Вейбулла –Гнеденко превращается в распределение Рэлея.

При m = 3,3 распределение Вейбулла – Гнеденко близко к нормальному.

Кроме рассмотренных законов распределения, в качестве моделей надёжности объектов могут использоваться и другие, например распределение Рэлея, распределение Эрланга и т. д. [53].
Контрольные вопросы

1. Перечислить виды распределений, описывающих надёжность в период постепенных отказов.

2. Для описания надёжности каких объектов используется логарифмически нормальное распределение?

3. Какой из параметров в выражении плотности распределения отказов при гамма-распределении наработки является параметром формы, а какой –параметром масштаба?

4.4. Совместное действие внезапных
и постепенных отказов

Вероятность безотказной работы изделия за период t, если до этого оно проработало время Т, по теореме умножения вероятностей:

P(t) = P_в(t) · P_п(t) , (4.37)

где

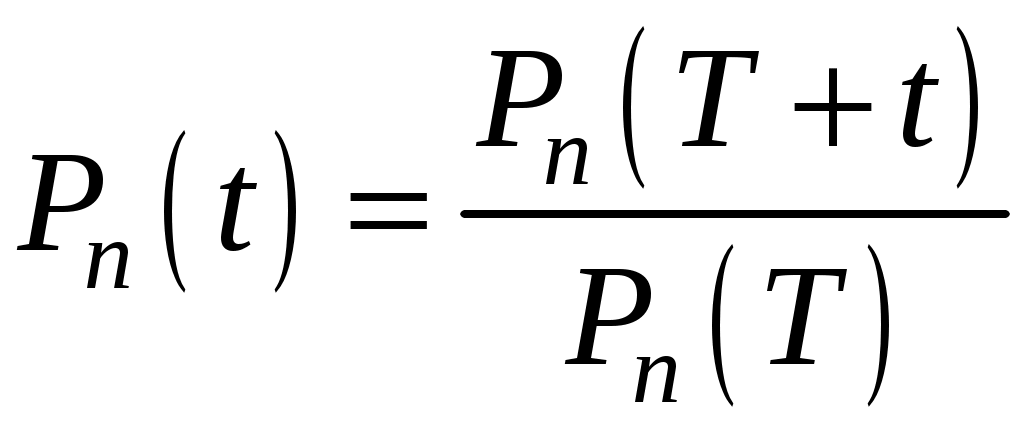– вероятности отсутствия внезапных и постепенных отказов соответственно.

, (4.38)

. (4.39)

На рис. 4.12 показаны вероятности отсутствия внезапных отказов и кривая вероятности безотказной работы при совместном действии внезапных и постепенных отказов.

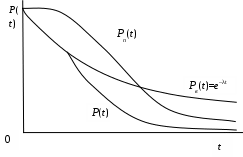
Рис. 4.12. Совместное действие внезапных и постепенных отказов
Вначале, когда интенсивность постепенных отказов низка, кривая P(t) соответствует кривой P_в(t), затем резко снижается.
4.5. Надёжность восстанавливаемых объектов.
Постановка задачи. Общая расчётная модель

При расчёте показателей надёжности восстанавливаемых объектов и систем наиболее распространено допущение:

– экспоненциальное распределение наработки между отказами;

– экспоненциальное распределение времени восстановления.

Допущение во многом справедливо, поскольку, во-первых, экспоненциальное распределение наработки описывает функционирование системы на участке нормальной эксплуатации, во-вторых, экспоненциальное распределение описывает процесс без «предыстории».

Применение экспоненциального распределения для описания процесса восстановления позволяет при независимых отказах представить анализируемые системы в виде марковских систем.

При экспоненциальном распределении наработки между отказами и времени восстановления расчёт надёжности производится методом дифференциальных уравнений для вероятностей состояний (уравнений Колмогорова –Чепмена).

Случайный процесс в какой-либо физической системе S называется марковским (рис. 4.13), если он обладает следующим свойством: для любого момента t₀ вероятность состояния системы в будущем (t > t₀) зависит только от состояния в настоящем (t = t₀) и не зависит от того, когда и каким образом система пришла в это состояние (иначе: при фиксированном настоящем будущее не зависит от предыстории процесса – прошлого).
t < t₀ t > t₀

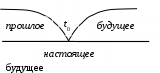
Рис. 4.13. Состояние системы
Для марковского процесса «будущее» зависит от «прошлого» только через «настоящее», т. е. будущее протекание процесса зависит только от тех прошедших событий, которые повлияли на состояние процесса в настоящий
момент.

Марковский процесс, как процесс без последействия, не означает полной независимости от прошлого, поскольку оно проявляется в настоящем.

В общем случае для системы S необходимо иметь математическую модель в виде множества состояний системы S₁, S₂, … , S_n

, в которых она может находиться при отказах и восстановлениях элементов.

Для рассмотрения принципа составления модели введены допущения:

– отказавшие элементы системы (или сам рассматриваемый объект) немедленно восстанавливаются (начало восстановления совпадает с моментом отказа);

– отсутствуют ограничения на число восстановлений;

– если все потоки событий, переводящих систему (объект) из состояния в состояние, являются пуассоновскими (простейшими), то случайный процесс переходов будет марковским процессом с непрерывным временем и дискретными состояниями S₁, S₂, … , S_n.

Основные правила составления модели:

1. Модель изображают в виде графа состояний.

Элементы графа:

а) кружки (вершины графа S₁, S₂, … , S_n) – возможные состояния системы S, возникающие при отказах элементов; б) стрелки – возможные направления переходов из одного состояния S_iв другое S_j.

Над/под стрелками указываются интенсивности переходов.

Рис. 4.14. Примеры графа: S₀ – работоспособное состояние; S₁– состояние отказа
«Петлей» обозначаются задержки в том или ином состоянии S₀и S₁, а именно:

S₀– исправное состояние продолжается;

S₁– состояние отказа продолжается (в дальнейшем петли на графах не рассматривают).

Граф состояний отражает конечное (дискретное) число возможных состояний системы S₁, S₂, …, S_n. Каждая из вершин графа соответствует одному из состояний.

2. Для описания случайного процесса перехода состояний (отказ/восстановление) применяют вероятности состояний P₁(t),P₂(t), … ,P_i(t),… ,P_n(t), где P_i(t) – вероятность нахождения системы в момент t в i-м состоянии, т. е. P_i(t) = P{S(t) = S_i}.

Очевидно, что для любого t

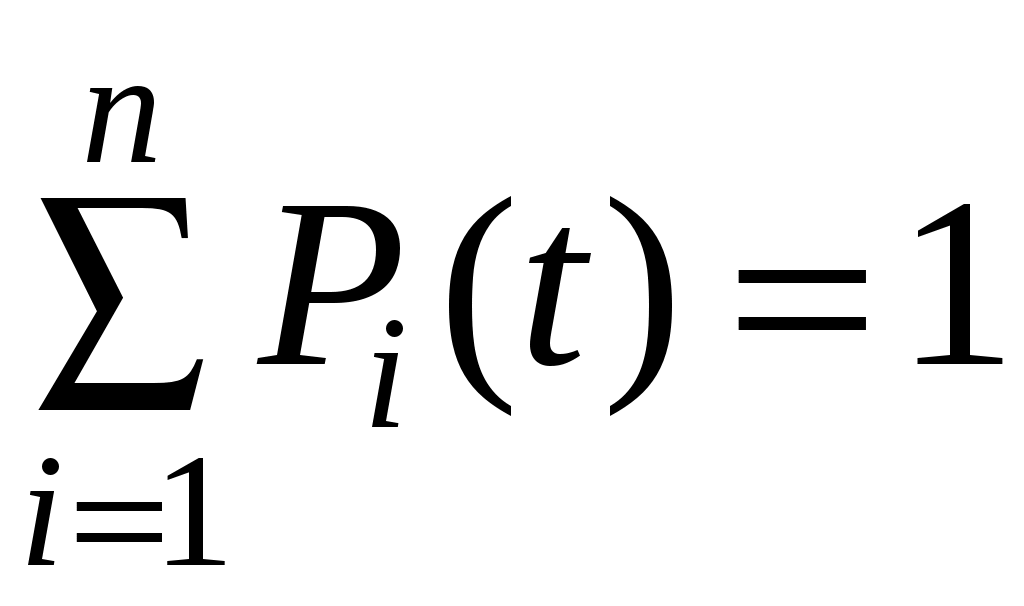. (4.40)

3. По графу состояний составляется система обыкновенных дифференциальных уравнений первого порядка (уравнений Колмогорова – Чепмена), имеющих вид:

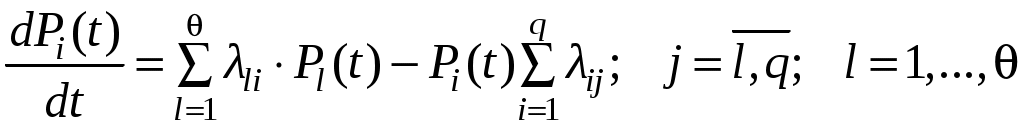
. (4.41)

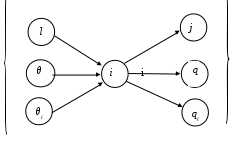
Рис. 4.15. Граф состояний
В общем случае интенсивности потоков λ_ij и μ_ij могут зависеть от вре-мени t.

При составлении дифференциальных уравнений пользуются простым мнемоническим правилом:

а) в левой части записывается производная по времени t от P_i(t);

б) в правой части число членов равно числу стрелок, соединяющих рассматриваемое состояние с другими состояниями;

в) каждый член правой части равен произведению интенсивности перехода на вероятность того состояния, из которого выходит стрелка;

г) знак произведения положителен, если стрелка входит (направлена острием) в рассматриваемое состояние, и отрицателен, если стрелка выходит из него.

Проверкой правильности составления уравнений является равенство нулю суммы правых частей уравнений.

4. Чтобы решить систему дифференциальных уравнений для вероятностей состояний P₁(t), P₂(t), …, P_i(t), …, P_n(t), необходимо задать начальное значение вероятностей P₁(0), P₂(t), …, P_i(0), …, P_n(0); при t = 0 их сумма равна единице:

.

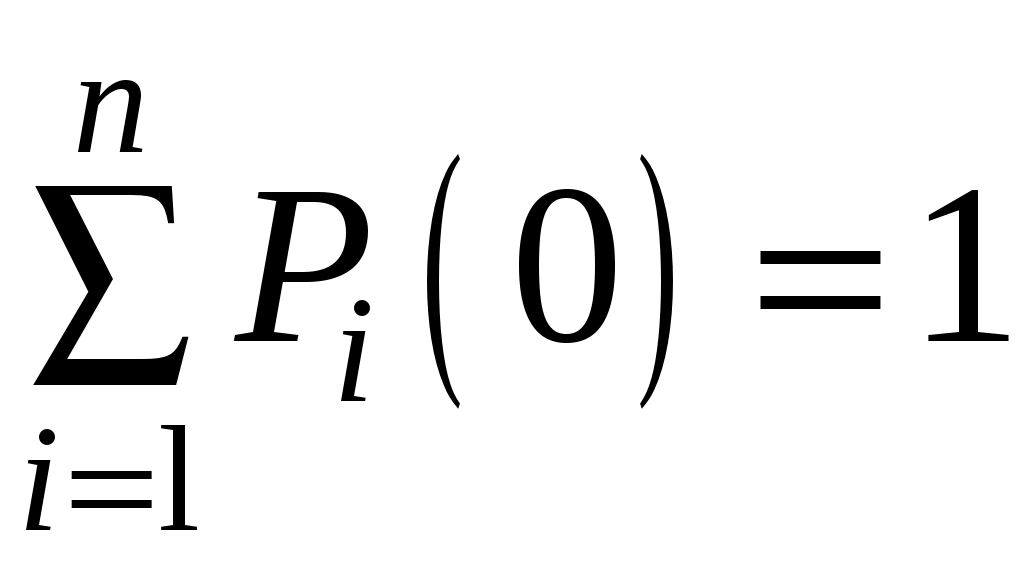Если в начальный момент t = 0 состояние системы известно, например, S(t = 0) = S_i, то P_i(0) = 1, а остальные равны нулю.

4.5.1. Показатели надёжности восстанавливаемых объектов

Все состояния системы S можно разделить на подмножества:

S_К S – подмножество состояний j =