Файл: Г. В. Савицкая Анализ хозяйственной деятельности предприятия.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 1267
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= ΔЧР × ГВф; ΔВПгв = ЧРпл × ΔГВ;
На графиках этим отклонениям соответствуют разные прямоугольники, так как при разных вариантах подстановки величина дополнительного прироста, результативного показателя, равная прямоугольнику ABCD, относится в первом случае к величине влияния годовой выработки, а во втором — к величине влияния количества рабочих. В результате этого величина влияния одного фактора преувеличивается, а другого — приуменьшается, что вызывает неоднозначность оценки влияния факторов, особенно в тех случаях, когда дополнительный прирост довольно существенный, как в нашем примере.
Чтобы избавиться от этого недостатка, в детерминированном факторном анализе используется интегральный метод, который применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида
Y =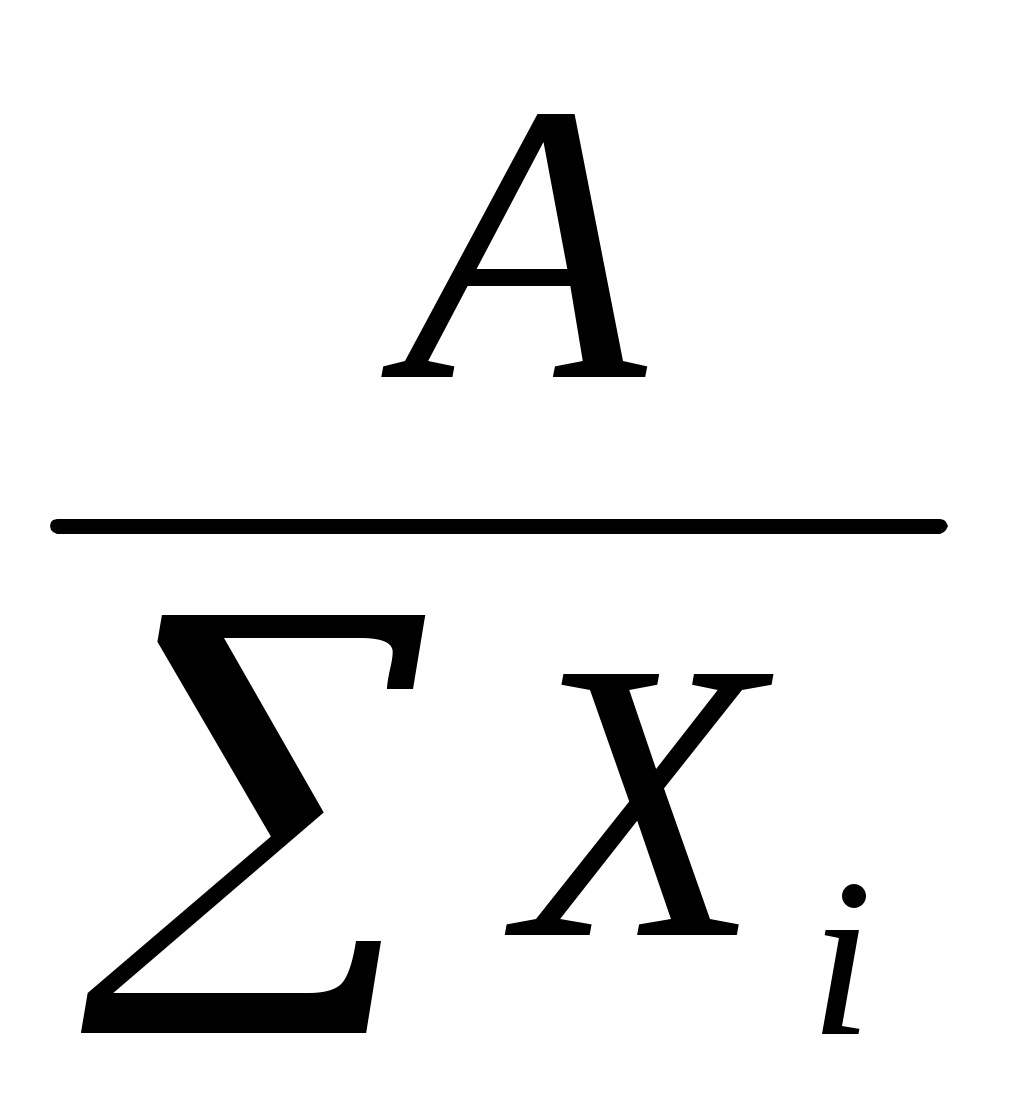
.
Использование этого способа позволяет получать более точные результаты расчета влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния факторов потому, что в данном случае результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, который образовался от взаимодействия факторов, раскладывается между ними поровну.
На первый взгляд может показаться, что для распределения дополнительного прироста достаточно взять его половину или часть, соответствующую количеству факторов. Но это сделать чаще всего сложно, так как факторы могут действовать в разных направлениях. Поэтому, применяя этот метод в АХД, пользуются готовыми алгоритмами, разработанными М.И. Бакановым и А.Д. Шереметом [5]. Приведем основные из них для разных моделей.
1. F = ХY
ΔFх = ΔХY0 + 1/2ΔХΔY; или АFх= 1/2ΔХ(Y0+ Y1);
ΔFу = ΔYХ0 +1/2 ΔХΔY; или ΔFу = 1/2 ΔY(Х0 + X1).
В нашем примере (см. табл. 6.1) расчет проводится следующим образом:
ΔВПчр = 200 × 160 + 1/2 (200 × 40) = 36 000 тыс. руб.;
ΔВПгв = 40 × 1000 + 1/2 (200 × 40) = 44 000 тыс. руб.
2. F = ХYZ
ΔFx= 1/2ΔХ(Y0Z1 + Y1Z
0) + l/3ΔХΔYΔZ;
ΔFу = 1/2ΔY(X0Z1 + X1Z0) + l/3ΔХΔYΔZ;
ΔFz = 1/2ΔZ(X0Y1 + Х1Y0) + l/3ΔХΔYΔZ.
Пример: ВП = ЧР×Д×ДВ:
ΔВПчр = 1/2 × 200(250 × 781,25 + 256 × 640) + 1/3 × 200 × 6 × 141,25 =+35 972;
ΔВПд = l/2 × 6 (1000 × 781,25 + 1200 × 640) + 1/3 × 200 × 6 × 141,25 = +4 704;
ΔВПдв= 1/2 × 141,25 (1000 × 256 + 1200 × 250) + 1/3 × 200 × 6 × 141,25 = 39 324
Всего +80 000 тыс. руб.
3. F= ХYZG
ΔFх = 1/6ΔХ{3Y0Z0G0+ Y1G0(Z1+ ΔZ) + G1Z0(Y1+ ΔY) + Z1Y0(G1 + ΔG)} +
+ 1/4 ΔХΔYΔZΔG;
ΔFу = 1/6ΔY{3Х0Z0G0 + ХlG0(Z1 + ΔZ) + G1Z0(X1 + ΔX) + Z1Х0(G1+ ΔG)} +
+ 1/4 ΔХΔYΔZΔG;
ΔFz = 1/6ΔZ{3Х0Y0G0 + G1X0(Y1 + ΔY) + Y1G0(X1 + ΔХ) + Х1Y0(G1+ ΔG)} +
+ 1/4 ΔXΔYΔZΔG;
ΔFg = 1/6 ΔG{3X0Y0Z0 + Z1X0(Y1+ ΔY) + Y1Z0(Х1 +ΔХ) + ХlY0(Zl+ ΔZ)} +
+ 1/4 ΔХΔYΔZΔG;
Пример: ВП = ЧР × Д × П × ЧВ:
ΔВПчр = 1/6 × 200 {3 × 250 × 8 × 80 + 256 × 80 (7,6 – 0,4) + 102,8 × 8 (256 +
+ 6) + 7,6 × 250 (102,796 + 22,796)} + 1/4 × 200 × 6 (–0,4) × 22,796 = +36 049 тыс. руб.;
ΔВПд = 1/6 × 6{3 × 1000 × 8 × 80 + 1200 × 80(7,6 – 0,4) + 102,796 × 8(1200 +
+ 200) + 7,6 × 1000 (102,796 + 22,796)} + 1/4 × 200 × 6 (–0,4) × 22,796 =
= +4714 тыс. руб.;
ΔВПп = 1/6 × (–0,4) {3 × 1000 × 250 × 80 + 102,796 × 1000 × (256 + 6) + 256 ×
× 80 (1200 + 200) + 1200 × 250 (102,796 + 22,796)} + 1/4 × 200 × 6 (-0,4) ×
× 22,796 = –10 221,5 тыс. руб.;
ΔВПчв = 1/6 × 22,769 {3 × 1000 × 250 × 8 + 7,6 × 1000 (256 + 6) + 256 ×
× 8(1200 + 200) + 1200 × 250 (7,6 – 0,4)} + 1∕4 × 200 × 6 (–0,4) × 22,796 =
= 49 458,5 тыс. руб.
Для расчета влияния факторов в кратных и смешанных моделях используются следующие рабочие формулы,
1. Вид факторной модели:
F =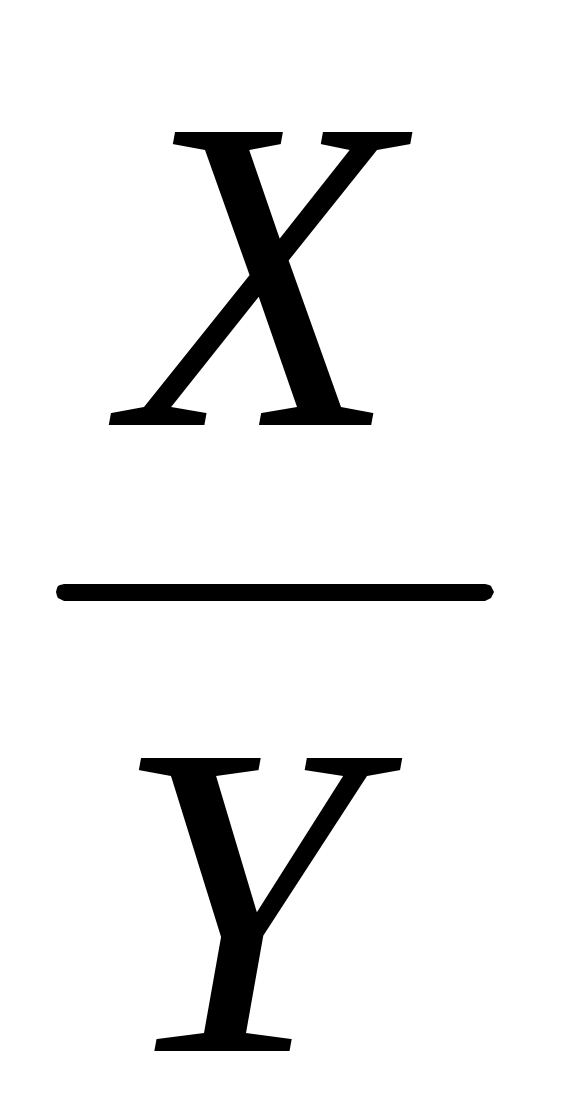
ΔFx =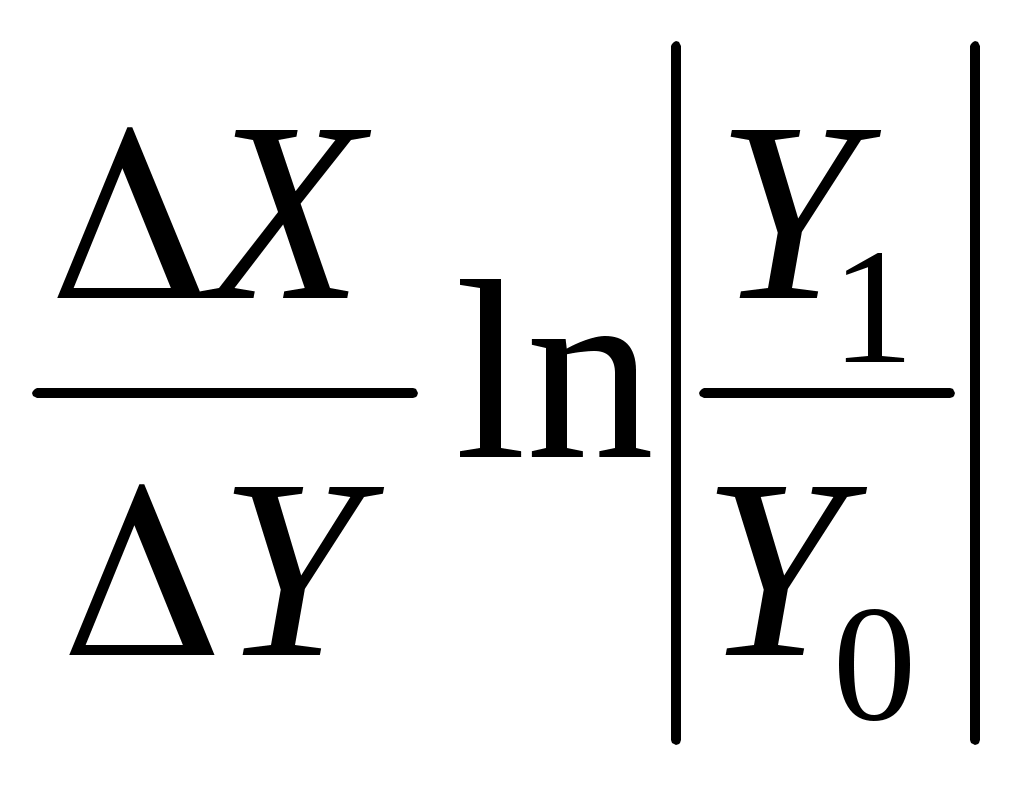
; ΔFy = ΔFобщ – ΔFx.
Пример:
ГВ =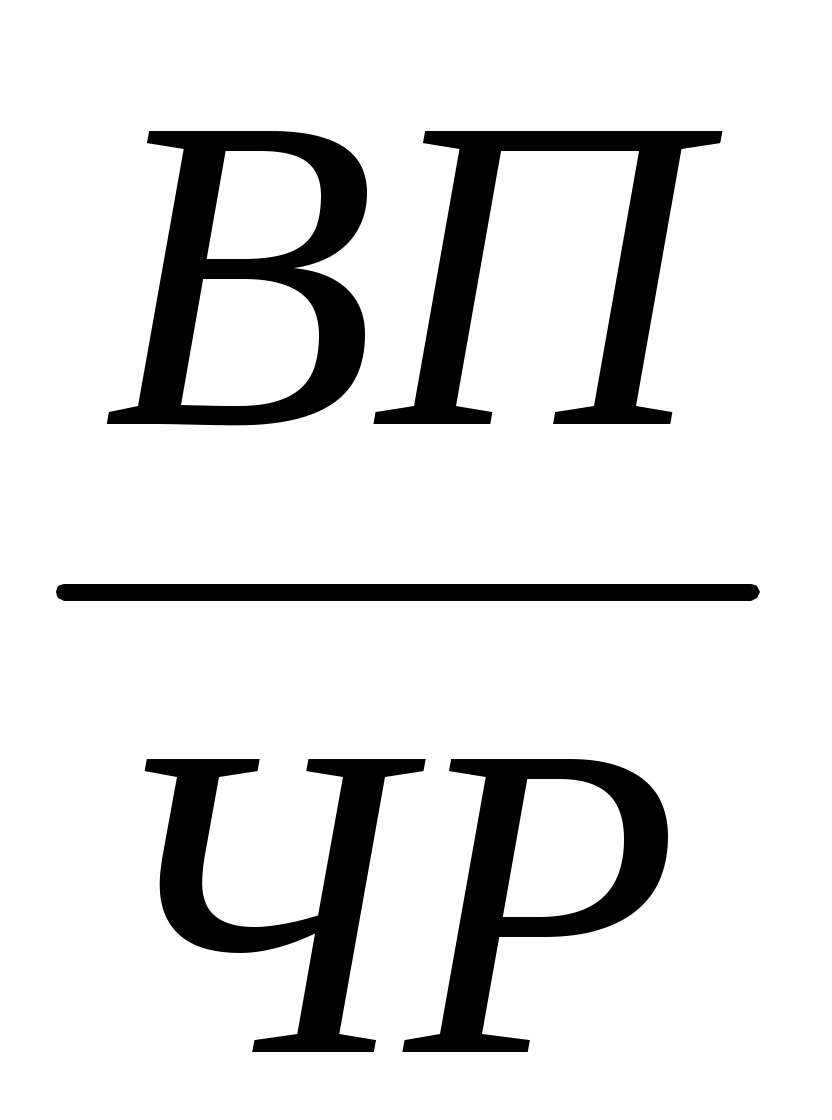
; ГВпл =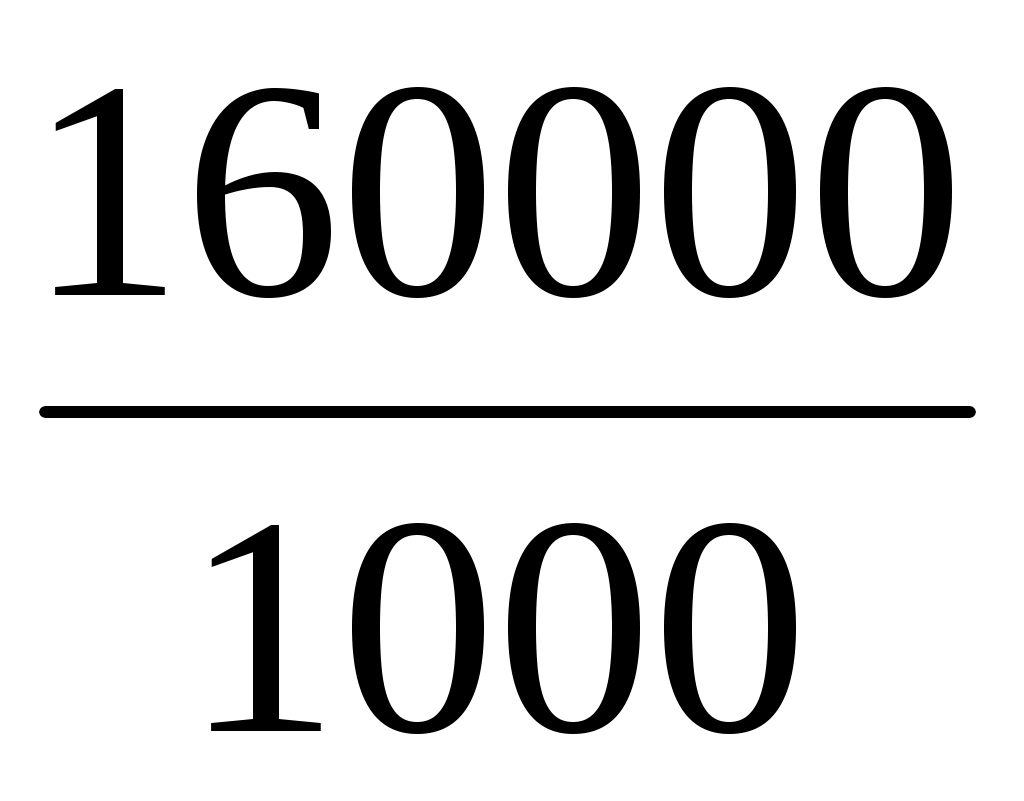
= 160; ГВф = 
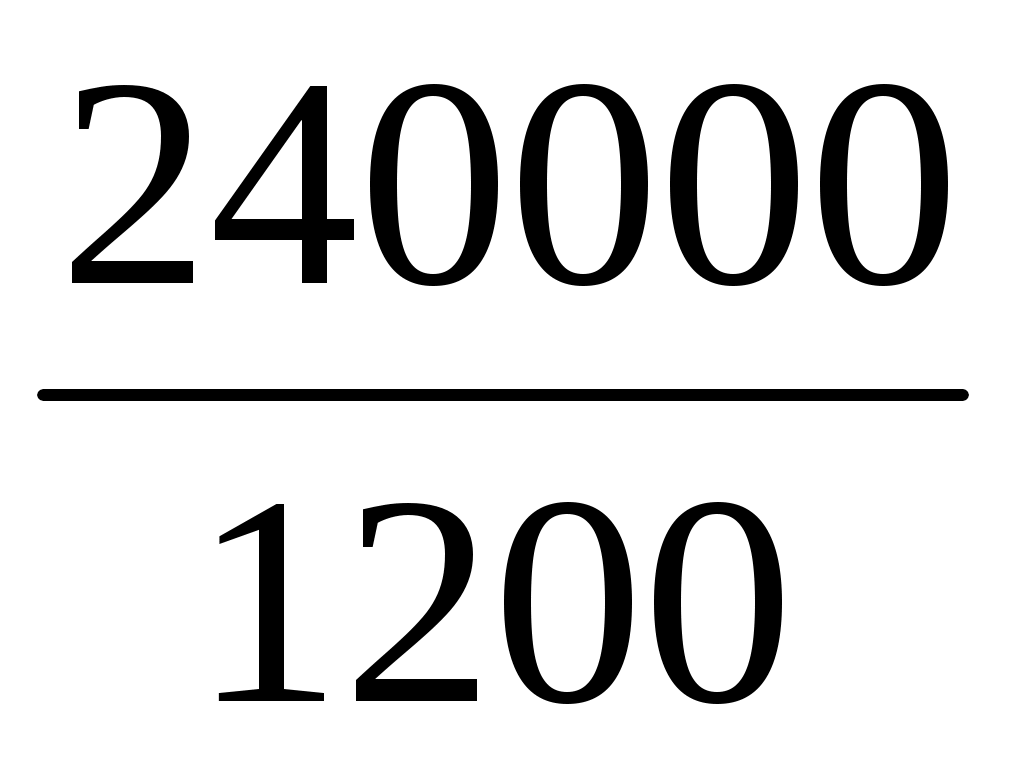= 200;
ΔГВвп =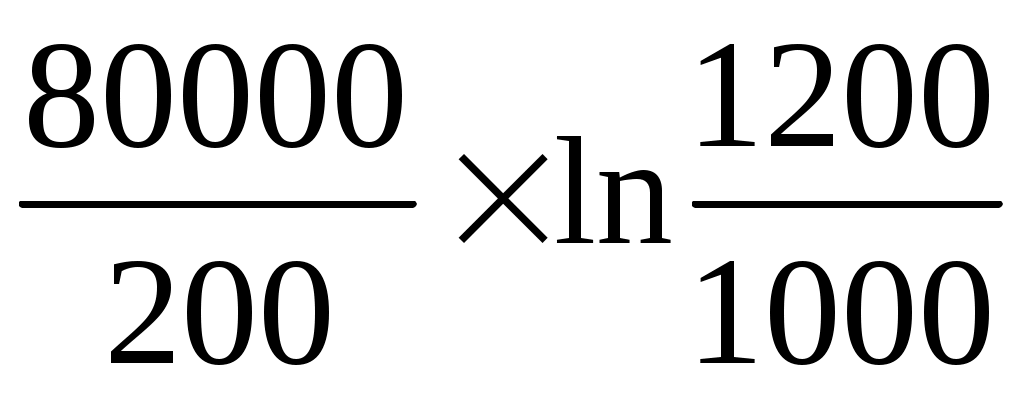
= 400 × ln1,2 = 400 × 0,182 = +73 тыс. руб.;
ΔГВчр = (200 – 160) –73 = 40 – 73 = –33 тыс. руб.
2. Вид факторной модели:
F =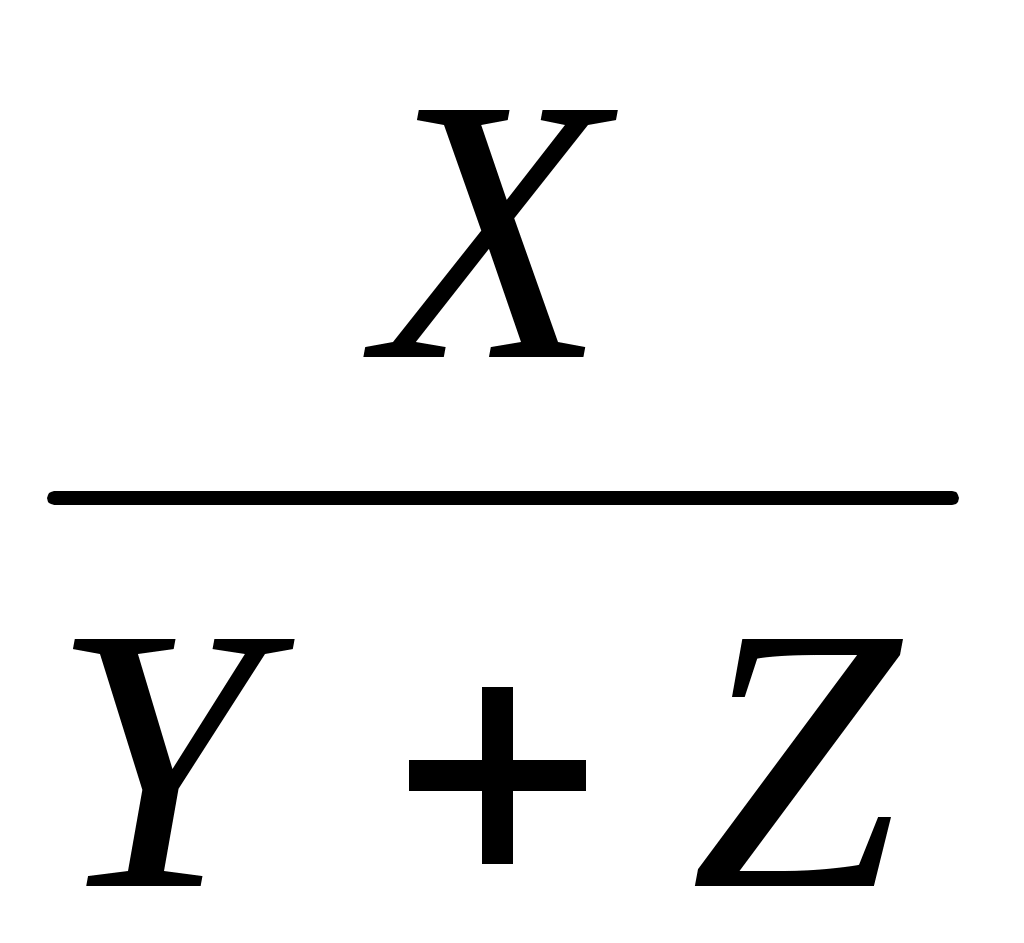
ΔFx =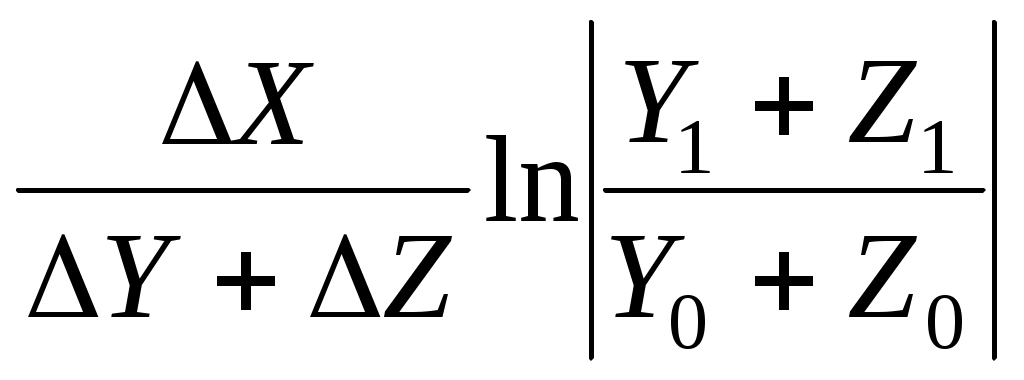
; ΔFy = 
;
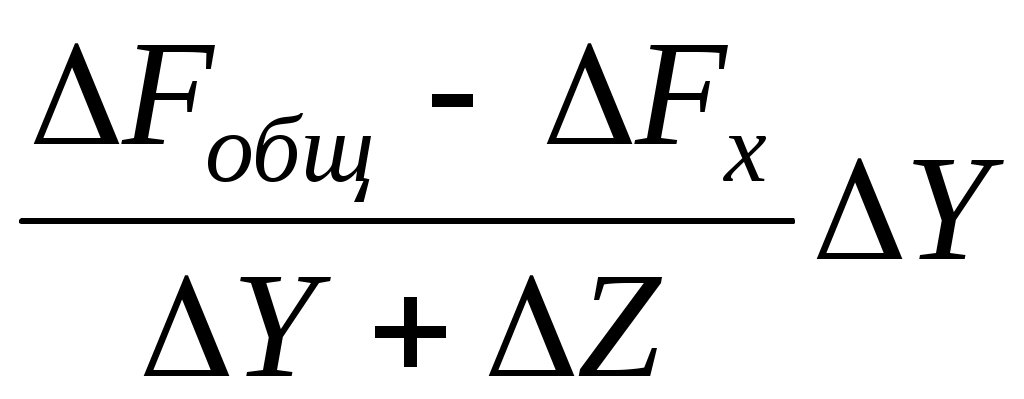ΔFz =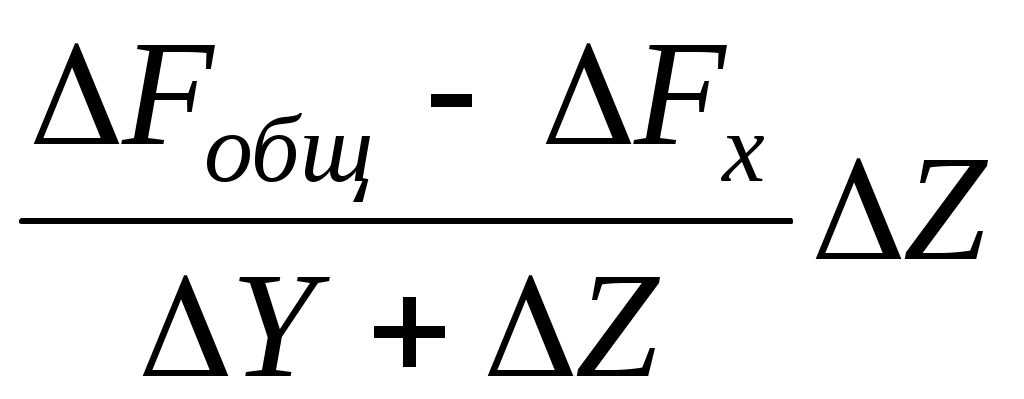
3. Вид факторной модели:
F =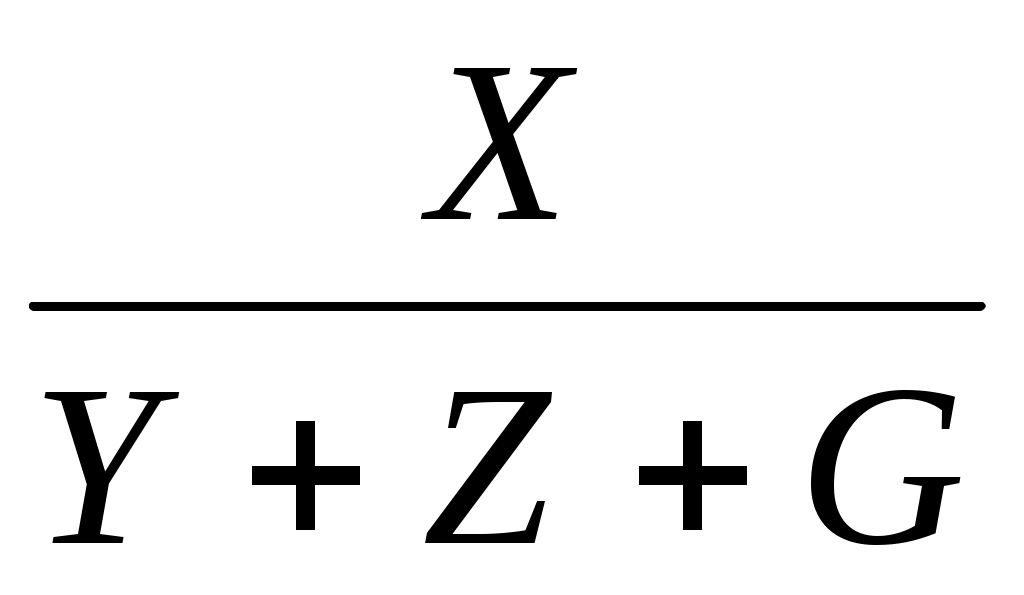
ΔFx =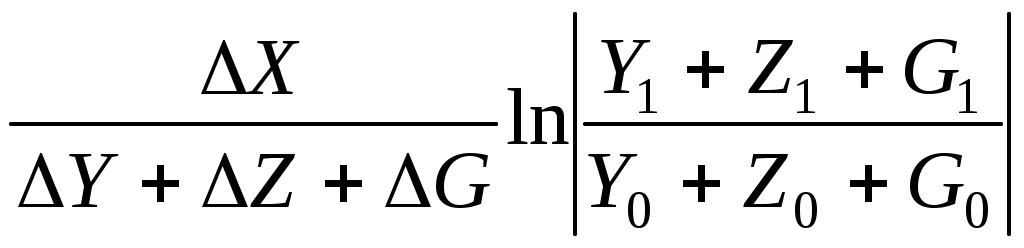
;
ΔFy =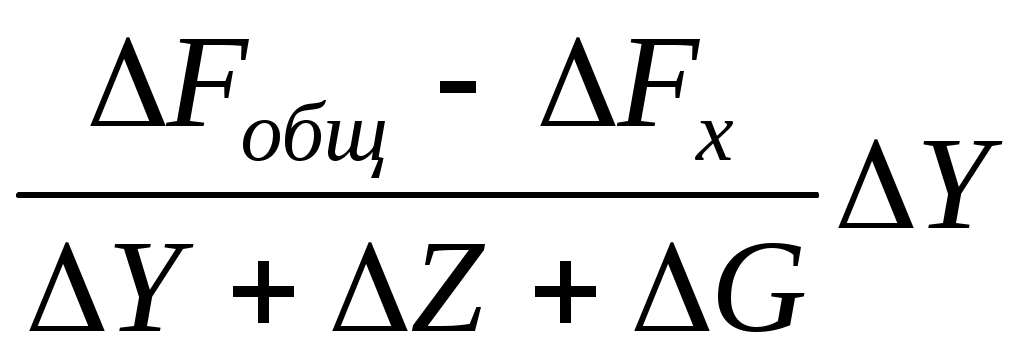
; ΔFz = 
;
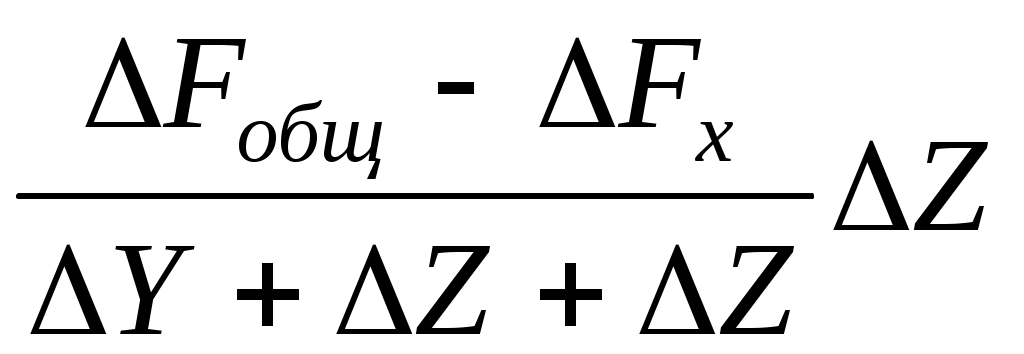ΔFg =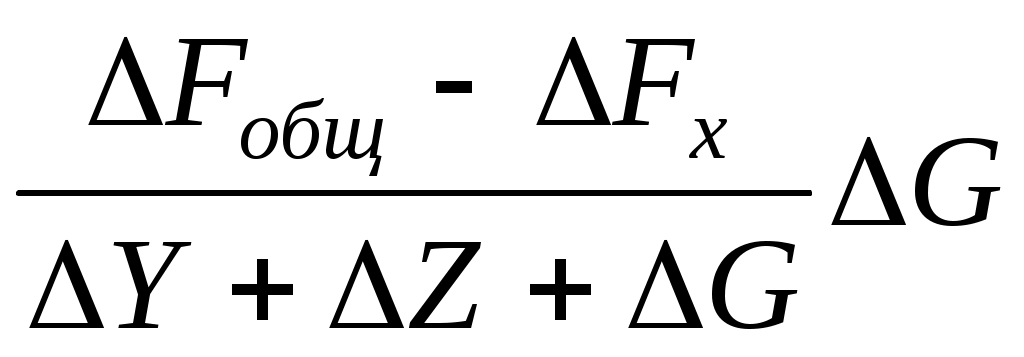
.
Таким образом, использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и сделать не очень сложные расчеты с помощью калькулятора или компьютера в Excel. При этом достигается более высокая точность расчетов.
6.7. Способ логарифмирования в анализе хозяйственной деятельности
Сущность, сфера применения и отличительные черты способа логарифмирования. Алгоритмы расчета влияния факторов этим способом.
Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. В данном случае результат расчета, как и при интегрировании, не зависит от месторасположения факторов в модели и по сравнению с интегральным методом обеспечивается еще более высокая точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В этом его преимущество, а недостаток — в ограниченности сферы применения.
В отличие от интегрального метода при логарифмировании используются не абсолютные приросты показателей, а индексы их роста (снижения).
Математически этот метод описывается следующим образом. Допустим, что результативный показатель можно представить в виде произведения трех факторов: f = xyz. Прологарифмировав обе части равенства, получим
lgf= lgx + lgy + lgz.
Учитывая, что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, произведем замену абсолютных их значений на индексы:
lg(f1/f0) = lg(x1/x0) + lg(y1/y0) + lg(z1/z0);
или
lgIf = lgIx + lgIy + lgIz.
Разделив обе части равенства на lgIf и умножив на Δf получим:
Δf =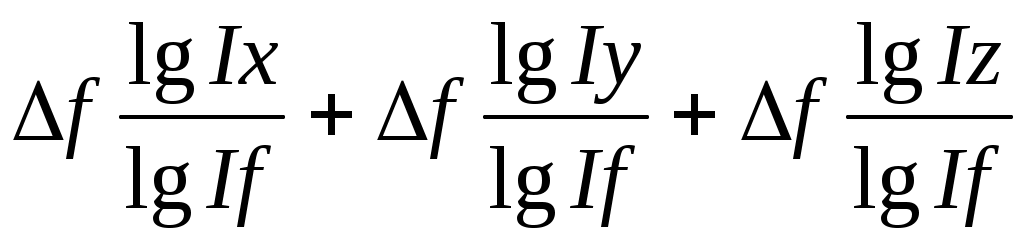
= Δfx + Δfy + Δfz.
Отсюда влияние факторов определяется следующим образом:
Δfx =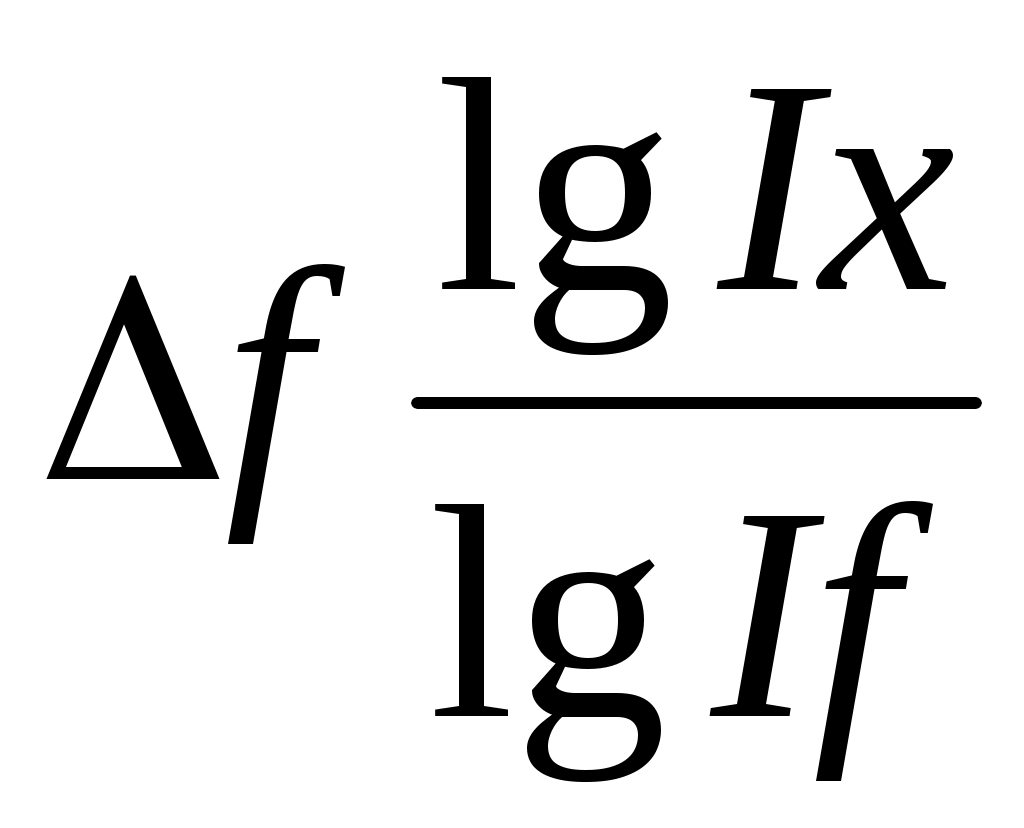
; Δfy = 
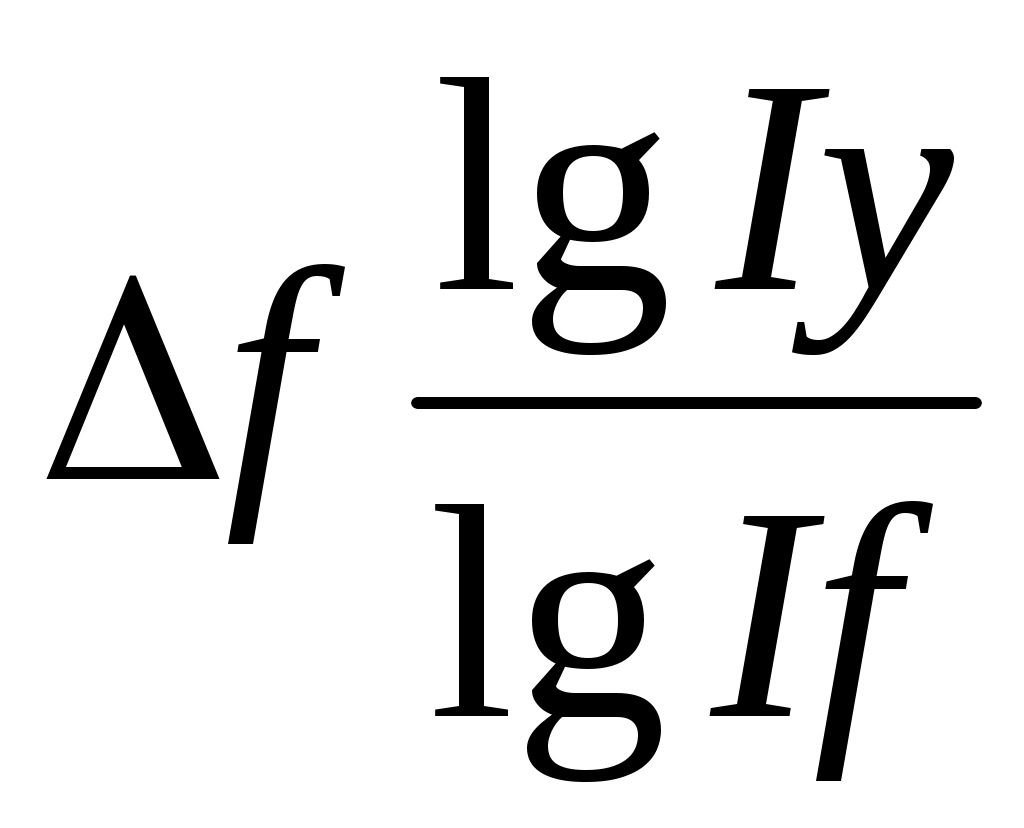; Δfz = 
.
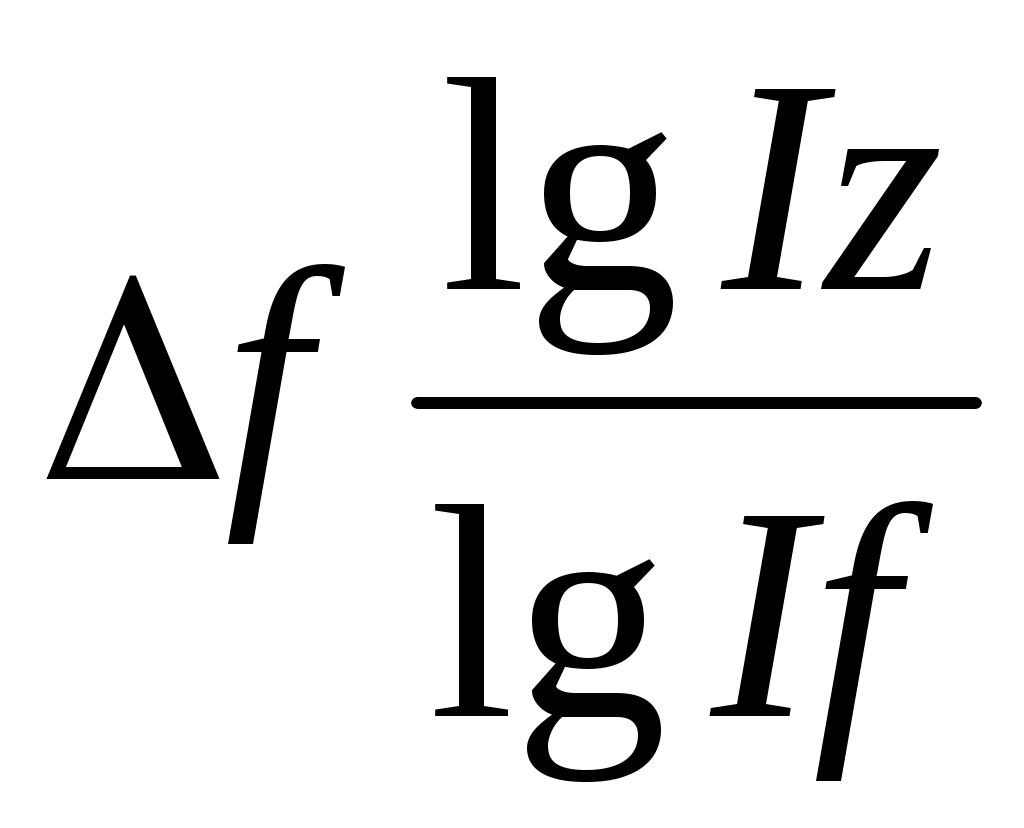Из формул вытекает, что общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму индекса результативного показателя. И не имеет значения, какой логарифм используется — натуральный или десятичный.
Используя данные табл. 6.1, вычислим прирост валовой продукции за счет численности рабочих (ЧР),количества отработанных дней одним рабочим за год (Д)и среднедневной выработки (ДВ) по факторной модели:
ВП = ЧР × Д × ДВ.
ΔВПчр = ΔВПобщ ×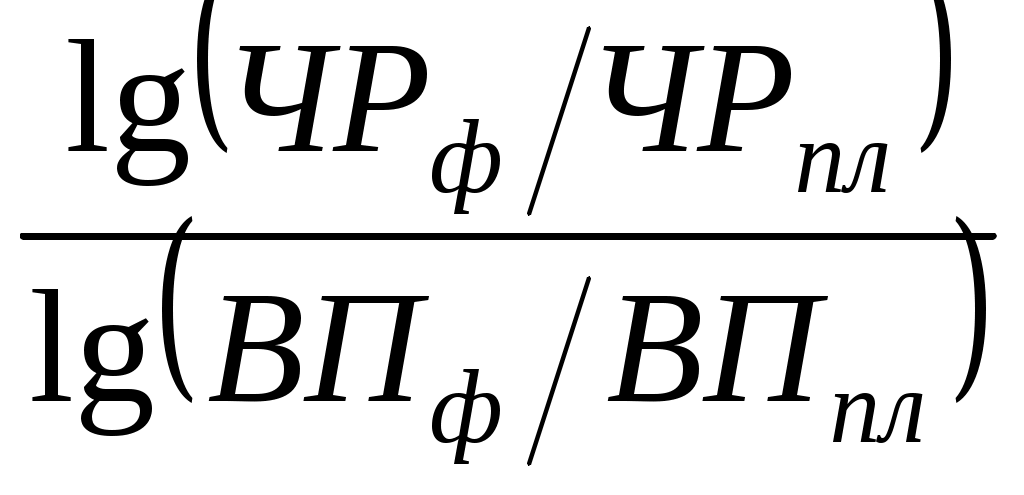
= 80 000 × 
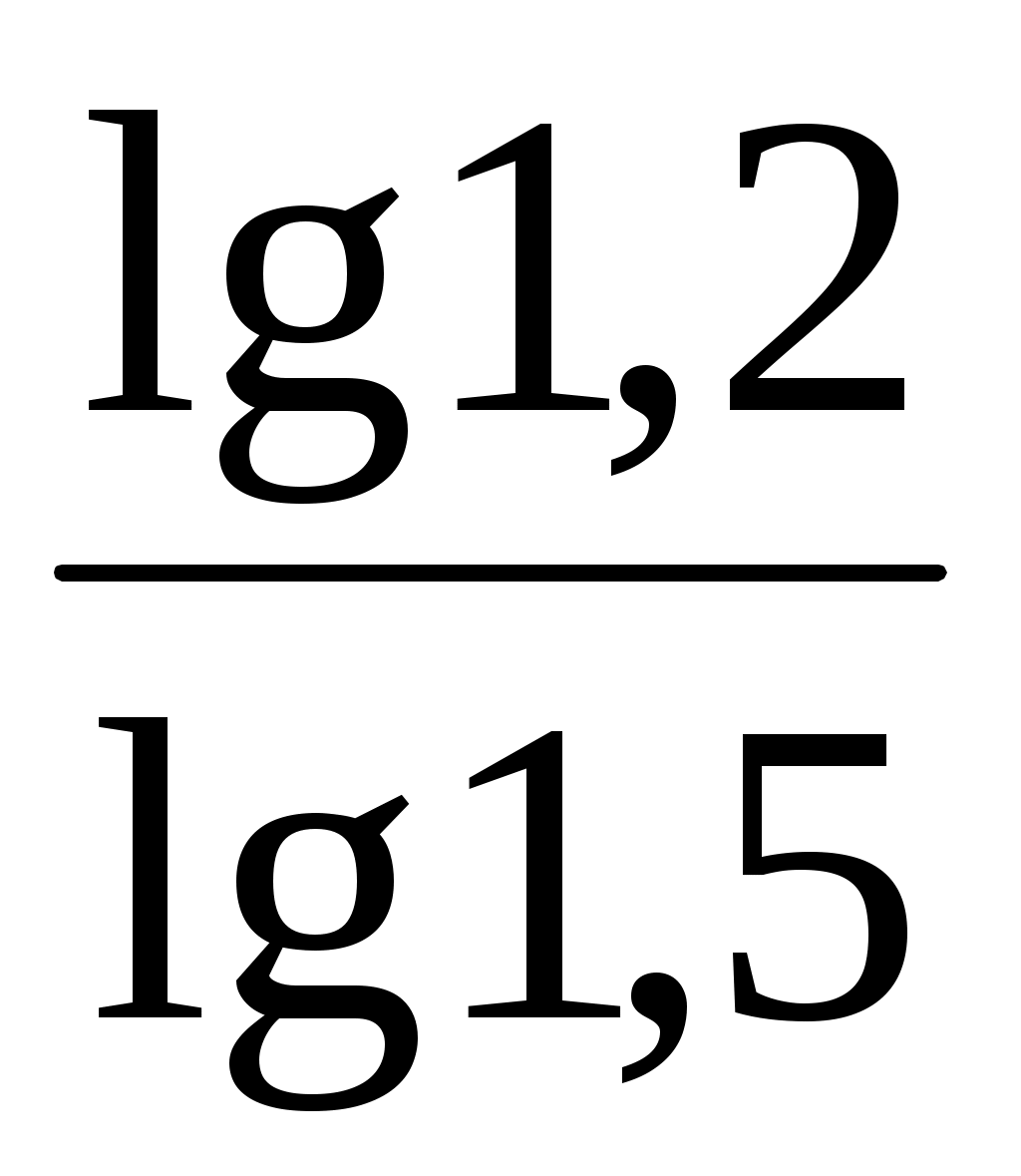= +35 973 тыс. руб.;
ΔВПд = ΔВПобщ ×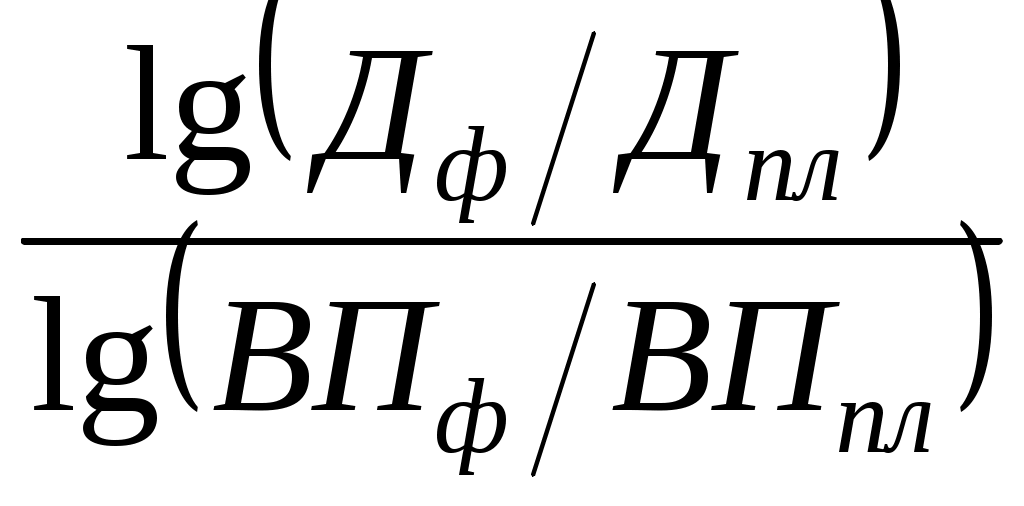
=80 000 × 
= +
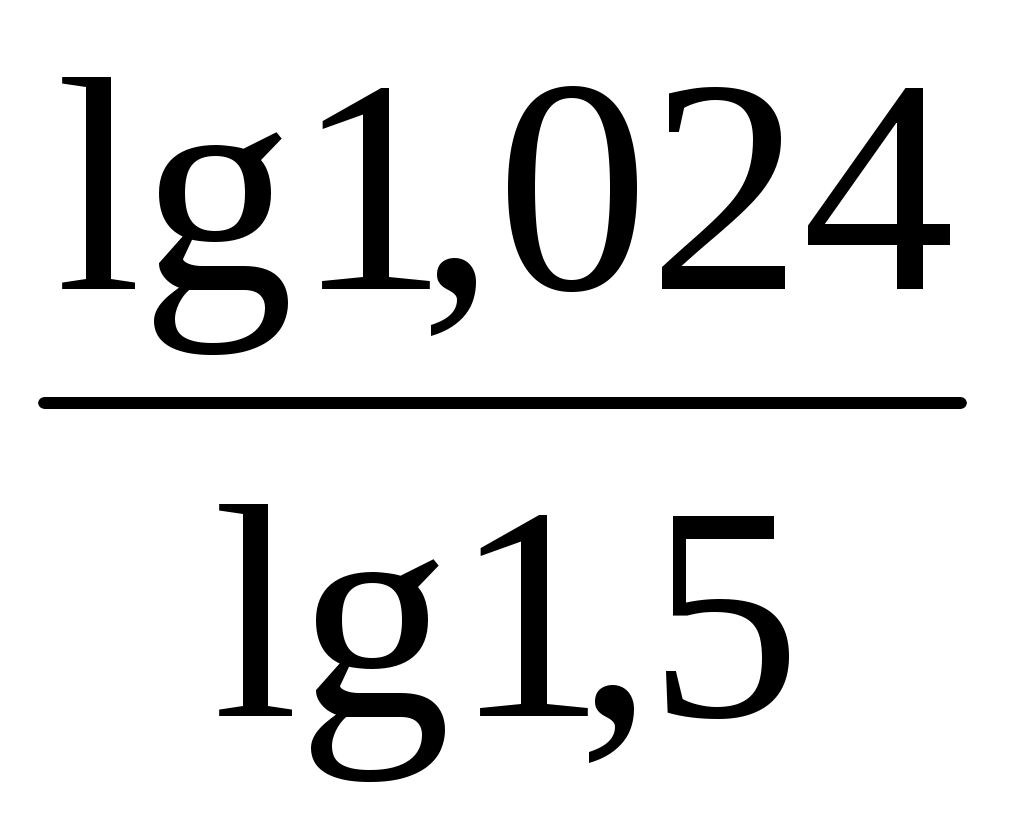4 680 тыс. руб.;
ΔВПдв = ΔВПобщ ×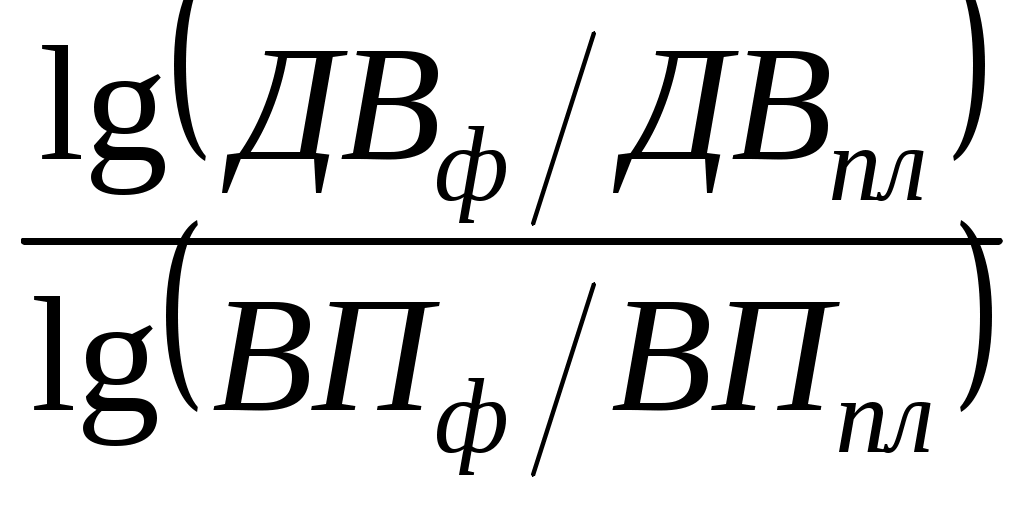
=80 000 × 
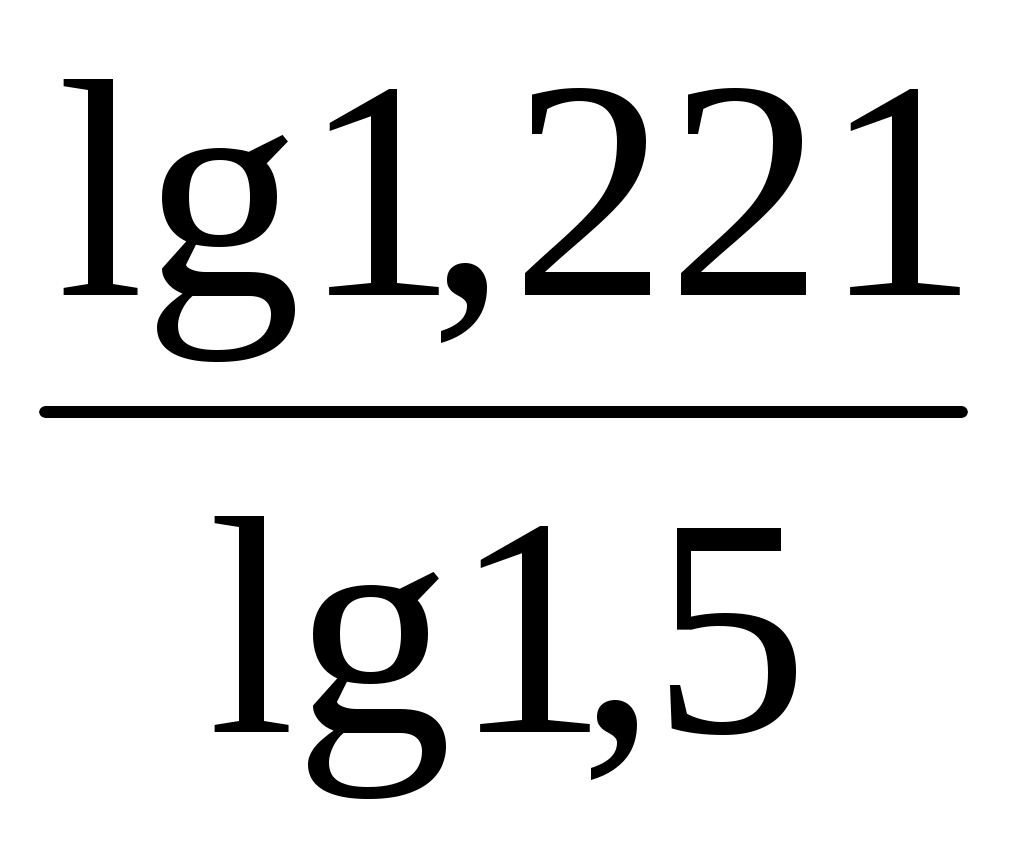= +39 347 тыс. руб.;
ΔВПобщ = ΔВПчр × ΔВПд × ΔВПдв.= 35 973 + 4680 + 39 347 = 80 000 тыс. руб.
Сравнив полученные результаты расчета влияния факторов разными способами по данной факторной модели, можно убедиться в преимуществе способа логарифмирования. Это выражается в относительной простоте вычислений и повышении точности расчетов.
Рассмотрев основные приемы детерминированного факторного анализа и сферу их применения, результаты можно систематизировать в виде следующей матрицы:
На графиках этим отклонениям соответствуют разные прямоугольники, так как при разных вариантах подстановки величина дополнительного прироста, результативного показателя, равная прямоугольнику ABCD, относится в первом случае к величине влияния годовой выработки, а во втором — к величине влияния количества рабочих. В результате этого величина влияния одного фактора преувеличивается, а другого — приуменьшается, что вызывает неоднозначность оценки влияния факторов, особенно в тех случаях, когда дополнительный прирост довольно существенный, как в нашем примере.
Чтобы избавиться от этого недостатка, в детерминированном факторном анализе используется интегральный метод, который применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида
Y =
.Использование этого способа позволяет получать более точные результаты расчета влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния факторов потому, что в данном случае результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, который образовался от взаимодействия факторов, раскладывается между ними поровну.
На первый взгляд может показаться, что для распределения дополнительного прироста достаточно взять его половину или часть, соответствующую количеству факторов. Но это сделать чаще всего сложно, так как факторы могут действовать в разных направлениях. Поэтому, применяя этот метод в АХД, пользуются готовыми алгоритмами, разработанными М.И. Бакановым и А.Д. Шереметом [5]. Приведем основные из них для разных моделей.
1. F = ХY
ΔFх = ΔХY0 + 1/2ΔХΔY; или АFх= 1/2ΔХ(Y0+ Y1);
ΔFу = ΔYХ0 +1/2 ΔХΔY; или ΔFу = 1/2 ΔY(Х0 + X1).
В нашем примере (см. табл. 6.1) расчет проводится следующим образом:
ΔВПчр = 200 × 160 + 1/2 (200 × 40) = 36 000 тыс. руб.;
ΔВПгв = 40 × 1000 + 1/2 (200 × 40) = 44 000 тыс. руб.
2. F = ХYZ
ΔFx= 1/2ΔХ(Y0Z1 + Y1Z
0) + l/3ΔХΔYΔZ;
ΔFу = 1/2ΔY(X0Z1 + X1Z0) + l/3ΔХΔYΔZ;
ΔFz = 1/2ΔZ(X0Y1 + Х1Y0) + l/3ΔХΔYΔZ.
Пример: ВП = ЧР×Д×ДВ:
ΔВПчр = 1/2 × 200(250 × 781,25 + 256 × 640) + 1/3 × 200 × 6 × 141,25 =+35 972;
ΔВПд = l/2 × 6 (1000 × 781,25 + 1200 × 640) + 1/3 × 200 × 6 × 141,25 = +4 704;
ΔВПдв= 1/2 × 141,25 (1000 × 256 + 1200 × 250) + 1/3 × 200 × 6 × 141,25 = 39 324
Всего +80 000 тыс. руб.
3. F= ХYZG
ΔFх = 1/6ΔХ{3Y0Z0G0+ Y1G0(Z1+ ΔZ) + G1Z0(Y1+ ΔY) + Z1Y0(G1 + ΔG)} +
+ 1/4 ΔХΔYΔZΔG;
ΔFу = 1/6ΔY{3Х0Z0G0 + ХlG0(Z1 + ΔZ) + G1Z0(X1 + ΔX) + Z1Х0(G1+ ΔG)} +
+ 1/4 ΔХΔYΔZΔG;
ΔFz = 1/6ΔZ{3Х0Y0G0 + G1X0(Y1 + ΔY) + Y1G0(X1 + ΔХ) + Х1Y0(G1+ ΔG)} +
+ 1/4 ΔXΔYΔZΔG;
ΔFg = 1/6 ΔG{3X0Y0Z0 + Z1X0(Y1+ ΔY) + Y1Z0(Х1 +ΔХ) + ХlY0(Zl+ ΔZ)} +
+ 1/4 ΔХΔYΔZΔG;
Пример: ВП = ЧР × Д × П × ЧВ:
ΔВПчр = 1/6 × 200 {3 × 250 × 8 × 80 + 256 × 80 (7,6 – 0,4) + 102,8 × 8 (256 +
+ 6) + 7,6 × 250 (102,796 + 22,796)} + 1/4 × 200 × 6 (–0,4) × 22,796 = +36 049 тыс. руб.;
ΔВПд = 1/6 × 6{3 × 1000 × 8 × 80 + 1200 × 80(7,6 – 0,4) + 102,796 × 8(1200 +
+ 200) + 7,6 × 1000 (102,796 + 22,796)} + 1/4 × 200 × 6 (–0,4) × 22,796 =
= +4714 тыс. руб.;
ΔВПп = 1/6 × (–0,4) {3 × 1000 × 250 × 80 + 102,796 × 1000 × (256 + 6) + 256 ×
× 80 (1200 + 200) + 1200 × 250 (102,796 + 22,796)} + 1/4 × 200 × 6 (-0,4) ×
× 22,796 = –10 221,5 тыс. руб.;
ΔВПчв = 1/6 × 22,769 {3 × 1000 × 250 × 8 + 7,6 × 1000 (256 + 6) + 256 ×
× 8(1200 + 200) + 1200 × 250 (7,6 – 0,4)} + 1∕4 × 200 × 6 (–0,4) × 22,796 =
= 49 458,5 тыс. руб.
Для расчета влияния факторов в кратных и смешанных моделях используются следующие рабочие формулы,
1. Вид факторной модели:
F =
ΔFx =
; ΔFy = ΔFобщ – ΔFx.Пример:
ГВ =
; ГВпл =
= 160; ГВф = = 200;ΔГВвп =
= 400 × ln1,2 = 400 × 0,182 = +73 тыс. руб.;ΔГВчр = (200 – 160) –73 = 40 – 73 = –33 тыс. руб.
2. Вид факторной модели:
F =
ΔFx =
; ΔFy = ;ΔFz =
3. Вид факторной модели:
F =
ΔFx =
;ΔFy =
; ΔFz = ;ΔFg =
.Таким образом, использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и сделать не очень сложные расчеты с помощью калькулятора или компьютера в Excel. При этом достигается более высокая точность расчетов.
6.7. Способ логарифмирования в анализе хозяйственной деятельности
Сущность, сфера применения и отличительные черты способа логарифмирования. Алгоритмы расчета влияния факторов этим способом.
Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. В данном случае результат расчета, как и при интегрировании, не зависит от месторасположения факторов в модели и по сравнению с интегральным методом обеспечивается еще более высокая точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В этом его преимущество, а недостаток — в ограниченности сферы применения.
В отличие от интегрального метода при логарифмировании используются не абсолютные приросты показателей, а индексы их роста (снижения).
Математически этот метод описывается следующим образом. Допустим, что результативный показатель можно представить в виде произведения трех факторов: f = xyz. Прологарифмировав обе части равенства, получим
lgf= lgx + lgy + lgz.
Учитывая, что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, произведем замену абсолютных их значений на индексы:
lg(f1/f0) = lg(x1/x0) + lg(y1/y0) + lg(z1/z0);
или
lgIf = lgIx + lgIy + lgIz.
Разделив обе части равенства на lgIf и умножив на Δf получим:
Δf =
= Δfx + Δfy + Δfz.Отсюда влияние факторов определяется следующим образом:
Δfx =
; Δfy = ; Δfz = .Из формул вытекает, что общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму индекса результативного показателя. И не имеет значения, какой логарифм используется — натуральный или десятичный.
Используя данные табл. 6.1, вычислим прирост валовой продукции за счет численности рабочих (ЧР),количества отработанных дней одним рабочим за год (Д)и среднедневной выработки (ДВ) по факторной модели:
ВП = ЧР × Д × ДВ.
ΔВПчр = ΔВПобщ ×
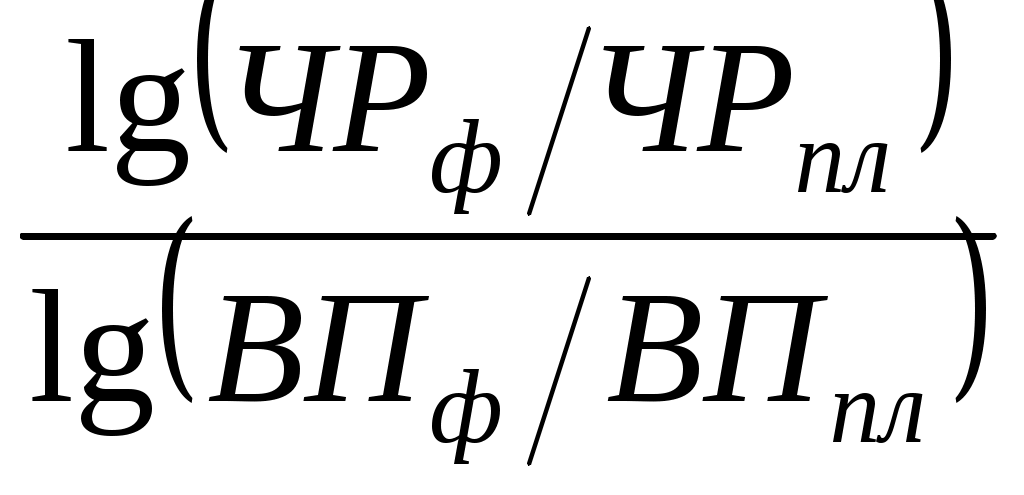= 80 000 × = +35 973 тыс. руб.;ΔВПд = ΔВПобщ ×
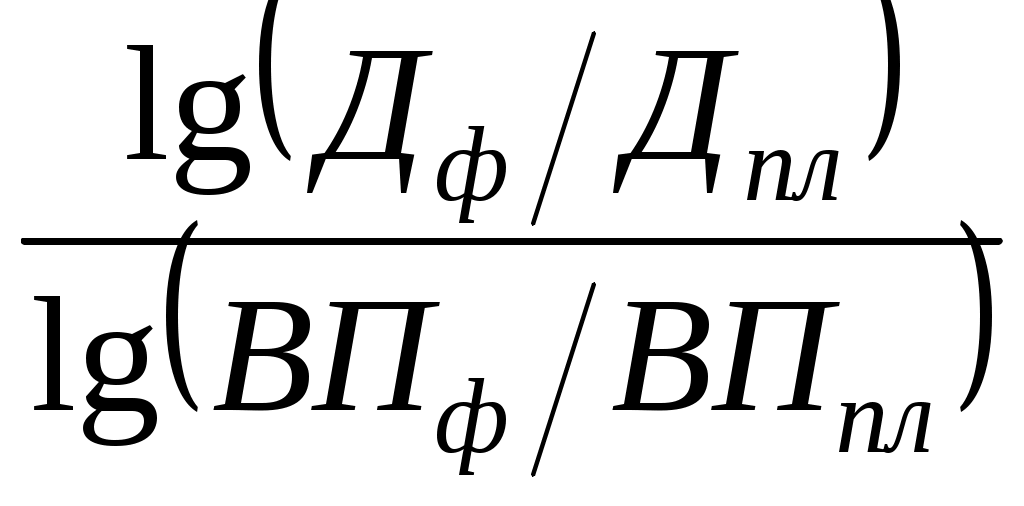=80 000 × = +
4 680 тыс. руб.;
ΔВПдв = ΔВПобщ ×
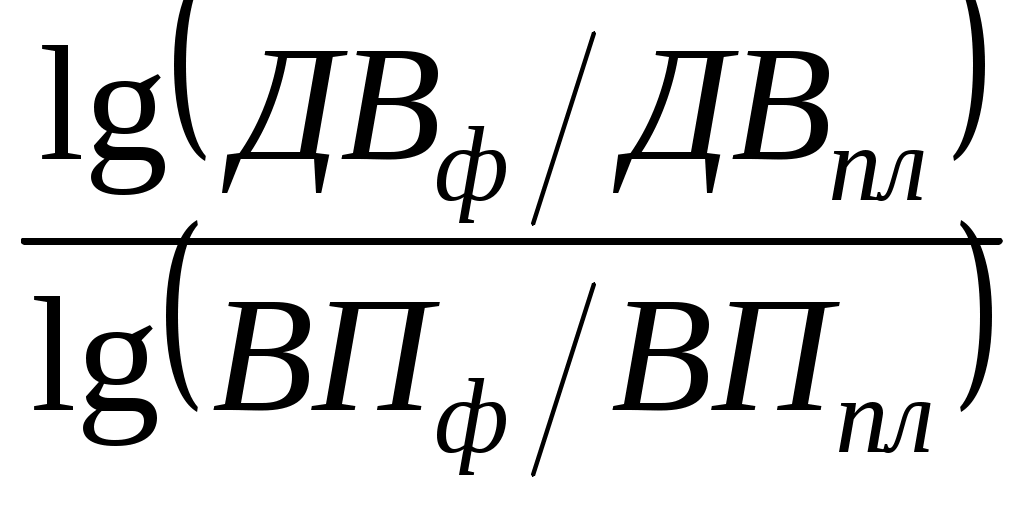=80 000 × = +39 347 тыс. руб.;ΔВПобщ = ΔВПчр × ΔВПд × ΔВПдв.= 35 973 + 4680 + 39 347 = 80 000 тыс. руб.
Сравнив полученные результаты расчета влияния факторов разными способами по данной факторной модели, можно убедиться в преимуществе способа логарифмирования. Это выражается в относительной простоте вычислений и повышении точности расчетов.
Рассмотрев основные приемы детерминированного факторного анализа и сферу их применения, результаты можно систематизировать в виде следующей матрицы:
| Прием | | Модели | | |
| Мультипликативные | Аддитивные | Кратные | Смешанные | |
| Цепной подстановки | + | + | + | + |
| Индексный | + | – | + | - |
| Абсолютных разниц | + | – | – | Y=а(b–с) |
| Относительных разниц | + | – | – | Y=(а–b)с |
| Пропорционального деления (долевого участия) | – | + | – | Y=а/∑xi |
| Интегральный | + | – | + | Y=а/∑xi |
| Логарифмирования | + | – | – | – |