Файл: Г. В. Савицкая Анализ хозяйственной деятельности предприятия.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 1272
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
у), для чего в полученное уравнение нужно подставить значения х и х2по каждой возрастной группе (табл. 7.3).
Т а б л и ц а 7.3
Расчет исходных данных для определения корреляционного отношения при криволинейных зависимостях
Подставив полученные значения в формулу (7.9),. определим величину корреляционного отношения:
η =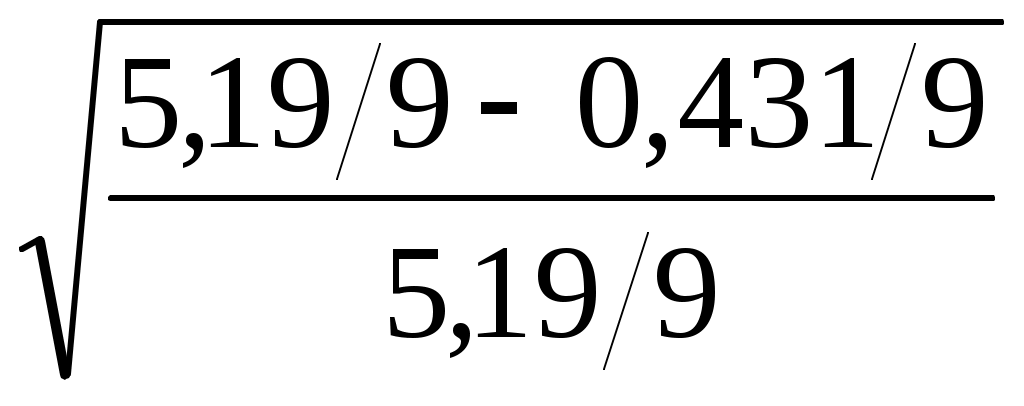
= 
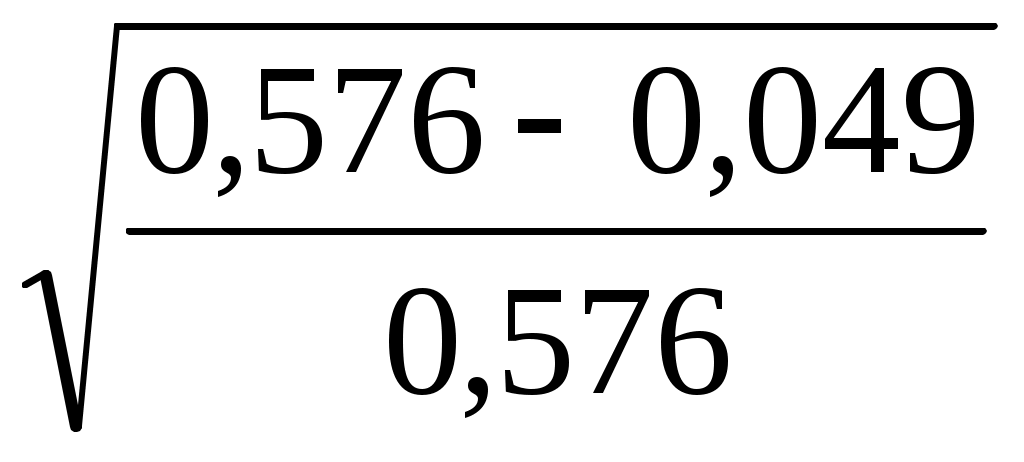= 0,956.
В заключение необходимо отметить
, что мы рассмотрели использование способов парной корреляции только на двух примерах. Однако эта методика может быть использована для исследования соотношений между разными экономическими показателями, что позволяет значительно углубить знания об изучаемых явлениях, определить место и роль каждого фактора в изменении уровня исследуемого показателя.
7.3. Методика множественного корреляционного анализа
Необходимость применения многофакторного корреляционного анализа. Этапы многофакторного корреляционного анализа. Правила отбора факторов для корреляционной модели. Обоснование необходимого объема выборки данных для корреляционного анализа. Сбор и статистическая оценка исходной информации. Способы обоснования уравнения связи. Основные показатели связи в корреляционном анализе и их интерпретация. Сущность парных (общих), частных и множественных коэффициентов корреляции и детерминации. Оценка значимости коэффициентов корреляции. Порядок расчета уравнения множественной регрессии. Интерпретация его параметров. Назначение коэффициентов эластичности и стандартизированных бетта-коэффициентов.
Экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества факторов. Как правило, каждый фактор в отдельности не определяет изучаемое явление во всей полноте. Только комплекс факторов в их взаимосвязи может дать более или менее полное представление о характере изучаемого явления.
Многофакторный корреляционный анализ состоит из нескольких этапов. На первом этапе определяются факторы, которые оказывают воздействие на изучаемый показатель, и отбираются наиболее существенные для корреляционного анализа.
На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа.
На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, то есть подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости.
На четвертом этапе проводится расчет основных показателей связи корреляционного анализа.
На пятом этапе дается статистическая оценка результатов корреляционного анализа и практическое их применение.
Отбор факторов для корреляционного анализа является очень важным моментом в экономическом анализе. От того, насколько правильно он сделан, зависит точность выводов по итогам анализа. Главная роль при отборе факторов принадлежит теории, а также практическому опыту анализа. При этом необходимо придерживаться следующих правил.
1. При отборе факторов в первую очередь следует учитывать причинно-следственные связи между показателями, так как только они раскрывают сущность изучаемых явлений. Анализ же таких факторов, которые находятся только в математических соотношениях с результативным показателем, не имеет практического смысла.
2. При создании многофакторкой корреляционной модели необходимо отбирать самые значимые факторы, которые оказывают решающее воздействие на результативный показатель, так как охватить все условия и обстоятельства практически невозможно. Факторы, которые имеют критерий надежности по Стьюденту меньше табличного, не рекомендуется принимать в расчет.
3. Все факторы должны быть количественно измеримы, т.е. иметь единицу измерения, и информация о них должна содержаться в учете и отчетности.
4. В корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем имеет криволинейный характер.
5. Не рекомендуется включать в корреляционную модель взаимосвязанные факторы. Если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из них необходимо исключить, иначе это приведет к искажению результатов анализа.
6. Нежелательно включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер.
Большую помощь при отборе факторов для корреляционной модели оказывают аналитические группировки, способ сопоставления параллельных и динамических рядов, линейные графики. Благодаря им можно определить наличие, направление и форму зависимости между изучаемыми показателями. Отбор факторов можно производить также в процессе решения задачи корреляционного анализа на основе оценки их значимости по критерию Стьюдента, о котором будет сказано ниже.
Исходя из перечисленных выше требований и используя названные способы отбора факторов, для многофакторной корреляционной модели уровня рентабельности (Y) подобраны следующие факторы, которые оказывают наиболее существенное влияние на ее уровень:
х1— материалоотдача, руб.;
х2 — фондоотдача, коп.;
х3— производительность труда (среднегодовая выработка продукции на одного работника), тыс. руб.;
х4— продолжительность оборота оборотных средств предприятия, дни;
х5— удельный вес продукции высшей категории качества, %.
Поскольку корреляционная связь с достаточной выразительностью и полнотой проявляется только в массе наблюдений, объем выборки данных должен быть достаточно большим, так как только в массе наблюдений сглаживается влияние других факторов. Чем большая совокупность объектов исследуется, тем точнее результаты анализа.
Учитывая это требование, влияние перечисленных факторов на уровень рентабельности исследуется на примере 40 предприятий.
Следующим этапом анализа является сбор и статистическая оценка исходной информации, которая будет использоваться в корреляционном анализе. Собранная исходная информация должна быть проверена на достоверность, однородность и соответствие закону нормального распределения.
В первую очередь необходимо убедиться в достоверности информации, насколько она соответствует объективной действительности. Использование недостоверной, неточной информации приведет к неправильным результатам анализа и выводам.
Одно из условий корреляционного анализа — однородность исследуемой информации относительно распределения ее около среднего уровня. Если в совокупности имеются группы объектов, которые значительно отличаются от среднего уровня, то это говорит о неоднородности исходной информации.
Критерием однородности информации служит среднеквадратическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю.
Среднеквадратическое отклонение показывает абсолютное отклонение индивидуальных значений от среднеарифметической. Оно определяется по формуле
σ =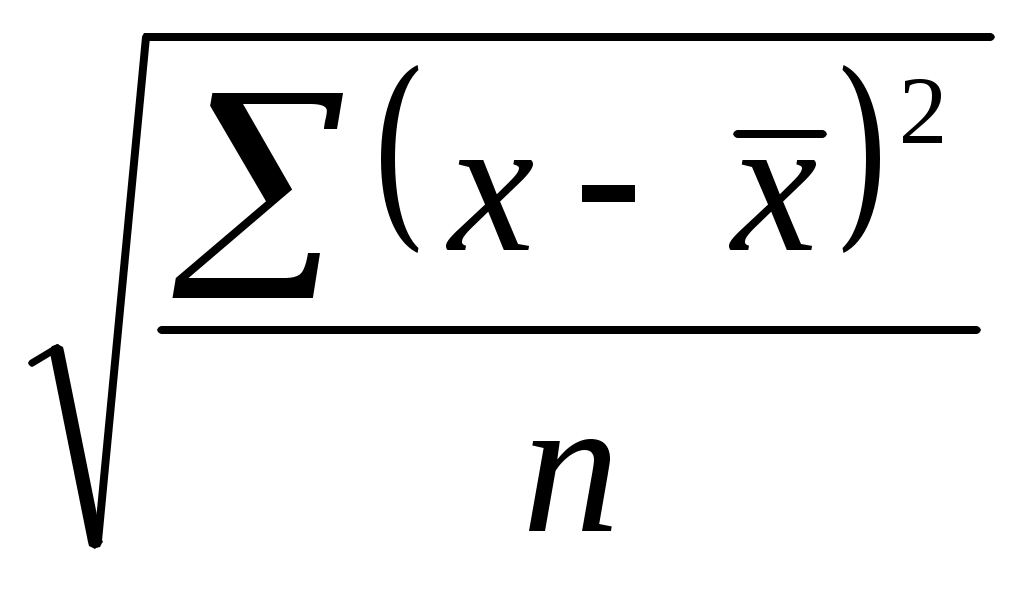
(7.10)
Коэффициент вариации характеризует относительную меру отклонения отдельных значений от среднеарифметической. Он рассчитывается по формуле
V =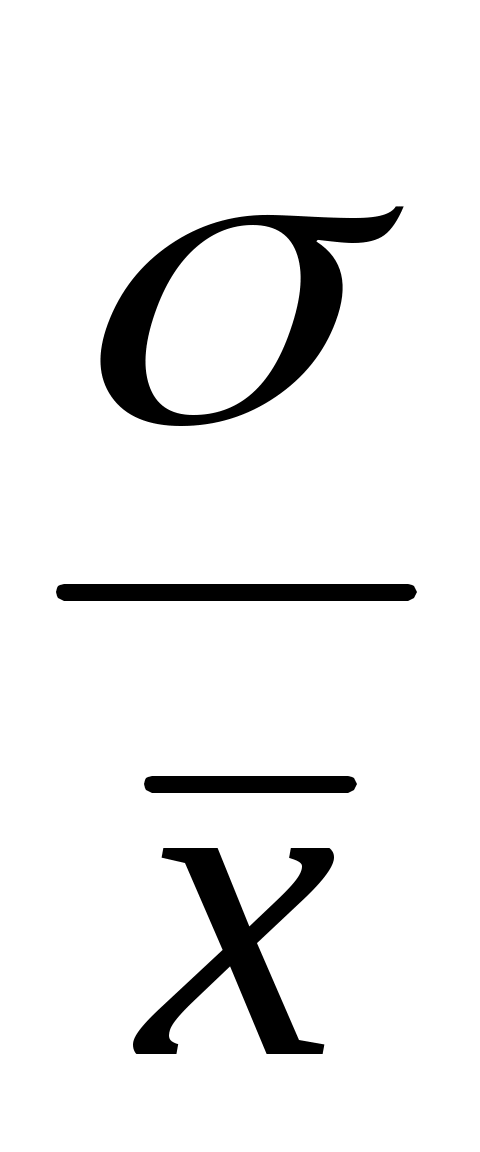
×100 (7.11)
Чем больше коэффициент вариации, тем относительно больший разброс и меньшая выравненность изучаемых объектов. Изменчивость вариационного ряда принято считать незначительной, если вариация не превышает 10 %, средней — если составляет 10-20 %, значительной — если она больше 20 %, но не превышает 33 %. Если же вариация выше 33 %, то это говорит о неоднородности информации и необходимости исключения нетипичных наблюдений, которые обычно бывают в первых и последних ранжированных рядах выборки.
В нашем примере (табл. 7.4) самая высокая вариация по х5 (V = 22,98), но она не превышает 33 %. Значит, исходная информация является однородной и ее можно использовать для дальнейших расчетов.
На основании самого высокого показателя вариации можно определить необходимый объем выборки данных для корреляционного анализа по следующей формуле:
n =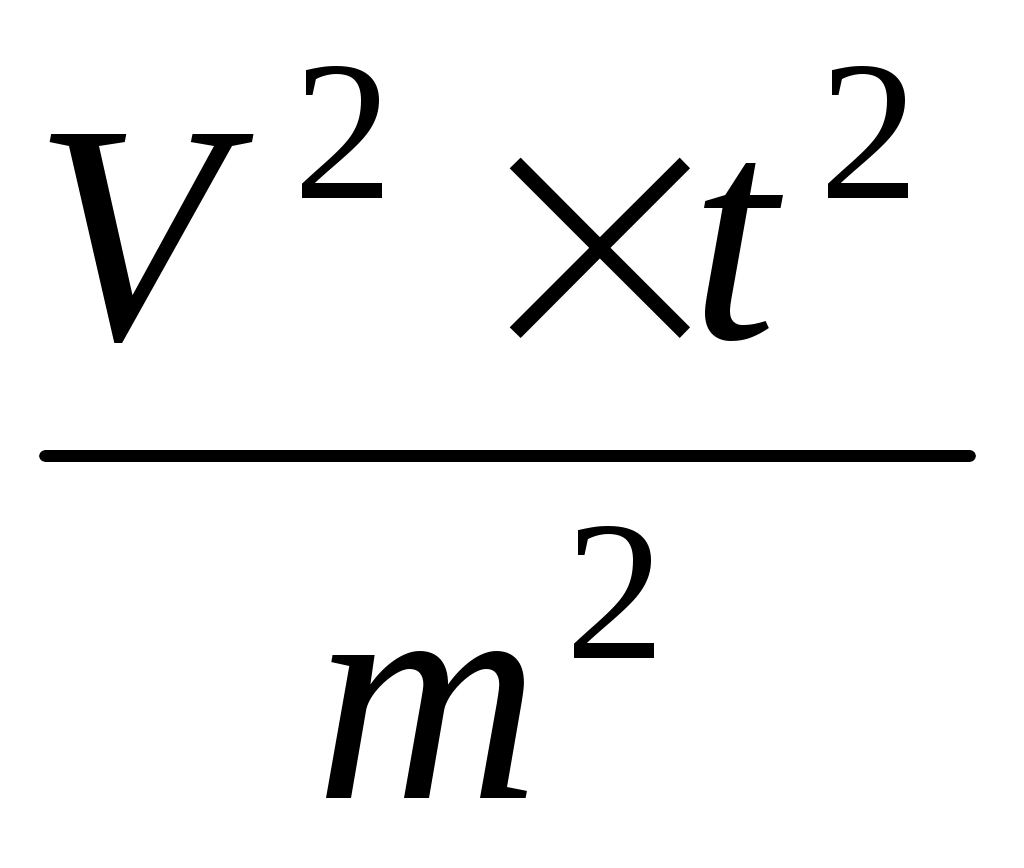
= 
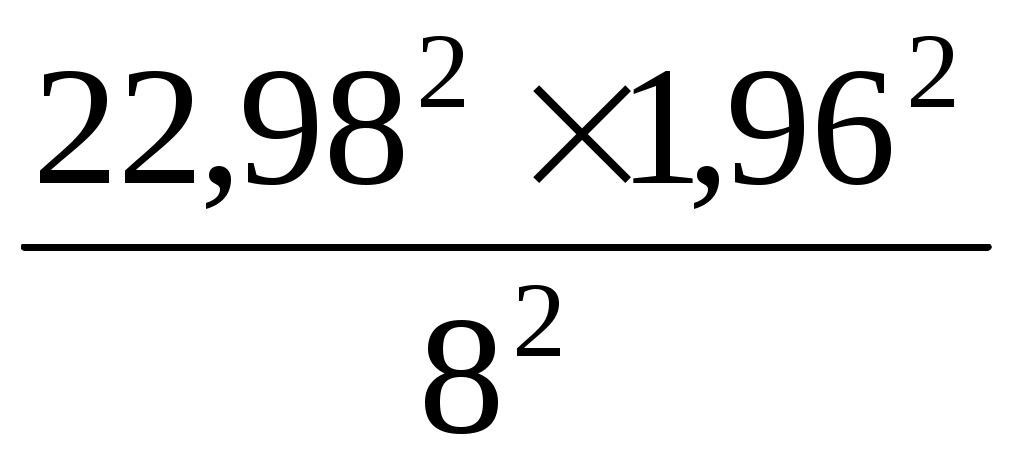= 32, (7.12)
где п — необходимый объем выборки данных;
V — вариация, %;
t — показатель надежности связи, который при уровне вероятности Р = 0,05 равен 1,96;
т — показатель точности расчетов (для экономических расчетов допускается ошибка 5 %.
Значит, принятый в расчет объем выборки (40 предприятий) является достаточным для проведения корреляционного анализа.
Таблица 7.4
Показатели статистической характеристики исходной информации
Т а б л и ц а 7.3
Расчет исходных данных для определения корреляционного отношения при криволинейных зависимостях
| у | ух | у-  | (y-  )2 | у - ух | (у-ух)2 |
| 4,2 | 3,93 | -0,9 | 0,81 | 0,27 | 0,073 |
| 4,8 | 4,9 | -0,3 | 0,09 | -0,1 | 0,01 |
| 5,3 | 5,55 | 0,2 | 0,04 | -0,25 | 0,062 |
| 6 | 5,95 | 0,9 | 0,81 | 0,05 | 0,003 |
| 6,2 | 6,05 | 1,1 | 1,21 | 0,15 | 0,022 |
| 5,8 | 5,9 | +0,7 | 0,49 | -0,1 | 0,01 |
| 5,3 | 5,43 | 0,2 | 0,04 | -0,13 | 0,017 |
| 4,4 | 4,78 | -0,7 | 0,49 | -0,38 | 0,144 |
| 4 | 3,7 | -1,1 | 1,21 | 0,3 | 0,09 |
| 46 | 46 | - | 5,19 | - | 0,431 |
Подставив полученные значения в формулу (7.9),. определим величину корреляционного отношения:
η =
= = 0,956.В заключение необходимо отметить
, что мы рассмотрели использование способов парной корреляции только на двух примерах. Однако эта методика может быть использована для исследования соотношений между разными экономическими показателями, что позволяет значительно углубить знания об изучаемых явлениях, определить место и роль каждого фактора в изменении уровня исследуемого показателя.
7.3. Методика множественного корреляционного анализа
Необходимость применения многофакторного корреляционного анализа. Этапы многофакторного корреляционного анализа. Правила отбора факторов для корреляционной модели. Обоснование необходимого объема выборки данных для корреляционного анализа. Сбор и статистическая оценка исходной информации. Способы обоснования уравнения связи. Основные показатели связи в корреляционном анализе и их интерпретация. Сущность парных (общих), частных и множественных коэффициентов корреляции и детерминации. Оценка значимости коэффициентов корреляции. Порядок расчета уравнения множественной регрессии. Интерпретация его параметров. Назначение коэффициентов эластичности и стандартизированных бетта-коэффициентов.
Экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества факторов. Как правило, каждый фактор в отдельности не определяет изучаемое явление во всей полноте. Только комплекс факторов в их взаимосвязи может дать более или менее полное представление о характере изучаемого явления.
Многофакторный корреляционный анализ состоит из нескольких этапов. На первом этапе определяются факторы, которые оказывают воздействие на изучаемый показатель, и отбираются наиболее существенные для корреляционного анализа.
На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа.
На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, то есть подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости.
На четвертом этапе проводится расчет основных показателей связи корреляционного анализа.
На пятом этапе дается статистическая оценка результатов корреляционного анализа и практическое их применение.
Отбор факторов для корреляционного анализа является очень важным моментом в экономическом анализе. От того, насколько правильно он сделан, зависит точность выводов по итогам анализа. Главная роль при отборе факторов принадлежит теории, а также практическому опыту анализа. При этом необходимо придерживаться следующих правил.
1. При отборе факторов в первую очередь следует учитывать причинно-следственные связи между показателями, так как только они раскрывают сущность изучаемых явлений. Анализ же таких факторов, которые находятся только в математических соотношениях с результативным показателем, не имеет практического смысла.
2. При создании многофакторкой корреляционной модели необходимо отбирать самые значимые факторы, которые оказывают решающее воздействие на результативный показатель, так как охватить все условия и обстоятельства практически невозможно. Факторы, которые имеют критерий надежности по Стьюденту меньше табличного, не рекомендуется принимать в расчет.
3. Все факторы должны быть количественно измеримы, т.е. иметь единицу измерения, и информация о них должна содержаться в учете и отчетности.
4. В корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем имеет криволинейный характер.
5. Не рекомендуется включать в корреляционную модель взаимосвязанные факторы. Если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из них необходимо исключить, иначе это приведет к искажению результатов анализа.
6. Нежелательно включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер.
Большую помощь при отборе факторов для корреляционной модели оказывают аналитические группировки, способ сопоставления параллельных и динамических рядов, линейные графики. Благодаря им можно определить наличие, направление и форму зависимости между изучаемыми показателями. Отбор факторов можно производить также в процессе решения задачи корреляционного анализа на основе оценки их значимости по критерию Стьюдента, о котором будет сказано ниже.
Исходя из перечисленных выше требований и используя названные способы отбора факторов, для многофакторной корреляционной модели уровня рентабельности (Y) подобраны следующие факторы, которые оказывают наиболее существенное влияние на ее уровень:
х1— материалоотдача, руб.;
х2 — фондоотдача, коп.;
х3— производительность труда (среднегодовая выработка продукции на одного работника), тыс. руб.;
х4— продолжительность оборота оборотных средств предприятия, дни;
х5— удельный вес продукции высшей категории качества, %.
Поскольку корреляционная связь с достаточной выразительностью и полнотой проявляется только в массе наблюдений, объем выборки данных должен быть достаточно большим, так как только в массе наблюдений сглаживается влияние других факторов. Чем большая совокупность объектов исследуется, тем точнее результаты анализа.
Учитывая это требование, влияние перечисленных факторов на уровень рентабельности исследуется на примере 40 предприятий.
Следующим этапом анализа является сбор и статистическая оценка исходной информации, которая будет использоваться в корреляционном анализе. Собранная исходная информация должна быть проверена на достоверность, однородность и соответствие закону нормального распределения.
В первую очередь необходимо убедиться в достоверности информации, насколько она соответствует объективной действительности. Использование недостоверной, неточной информации приведет к неправильным результатам анализа и выводам.
Одно из условий корреляционного анализа — однородность исследуемой информации относительно распределения ее около среднего уровня. Если в совокупности имеются группы объектов, которые значительно отличаются от среднего уровня, то это говорит о неоднородности исходной информации.
Критерием однородности информации служит среднеквадратическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю.
Среднеквадратическое отклонение показывает абсолютное отклонение индивидуальных значений от среднеарифметической. Оно определяется по формуле
σ =
(7.10)Коэффициент вариации характеризует относительную меру отклонения отдельных значений от среднеарифметической. Он рассчитывается по формуле
V =
×100 (7.11)Чем больше коэффициент вариации, тем относительно больший разброс и меньшая выравненность изучаемых объектов. Изменчивость вариационного ряда принято считать незначительной, если вариация не превышает 10 %, средней — если составляет 10-20 %, значительной — если она больше 20 %, но не превышает 33 %. Если же вариация выше 33 %, то это говорит о неоднородности информации и необходимости исключения нетипичных наблюдений, которые обычно бывают в первых и последних ранжированных рядах выборки.
В нашем примере (табл. 7.4) самая высокая вариация по х5 (V = 22,98), но она не превышает 33 %. Значит, исходная информация является однородной и ее можно использовать для дальнейших расчетов.
На основании самого высокого показателя вариации можно определить необходимый объем выборки данных для корреляционного анализа по следующей формуле:
n =
= = 32, (7.12)где п — необходимый объем выборки данных;
V — вариация, %;
t — показатель надежности связи, который при уровне вероятности Р = 0,05 равен 1,96;
т — показатель точности расчетов (для экономических расчетов допускается ошибка 5 %.
Значит, принятый в расчет объем выборки (40 предприятий) является достаточным для проведения корреляционного анализа.
Таблица 7.4
Показатели статистической характеристики исходной информации
| Номер переменной | Среднеарифметическое значение | Среднеквадратическое отклонение | Вариация, % | Асимметрия | Эксцесс | Ошибка | |
| асимметрии | эксцесса | ||||||
| Y | 27,15 | 2,85 | 10,5 | 0,20 | -1,16 | 0,37 | 0,73 |
| х1 | 2,77 | 0,28 | 10,08 | 0,36 | -0,81 | 0,37 | 0,73 |
| х2 | 92,57 | 8,70 | 9,39 | 0,24 | -0,69 | 0,37 | 0,73 |
| х3 | 8,46 | 0,59 | 7,00 | 0,10 | -0,52 | 0,37 | 0,73 |
| х4 | 17,77 | 2,76 | 15,55 | 0,72 | -0,08 | 0,37 | 0,73 |
| х5 | 31,68 | 7,28 | 22,98 | 0,63 | -0,13 | 0,37 | 0,73 |