Файл: Г. В. Савицкая Анализ хозяйственной деятельности предприятия.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 1280
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
его оплаты. Поэтому в общем виде взаимосвязь между уровнем рентабельности и уровнем оплаты труда будет прямой. Если взять непосредственную связь между этими показателями при условии неизменности производительности труда и других факторов, то получится, что при повышении оплаты труда рентабельность понижается. Здесь уже обратная зависимость и частный коэффициент корреляции будет со знаком минус.
Т а б л и ц а 7.7
Матрица частных коэффициентов корреляции
Таким образом, с помощью парных и частных коэффициентов корреляции можно получить представление о тесноте связи между изучаемыми явлениями в общих и непосредственных соприкосновениях.
Значительный интерес представляют коэффициенты корреляции, характеризующие взаимосвязь факторов между собой. Как уже отмечалось, в корреляционную модель надо подбирать независимые между собой факторы. Если коэффициент корреляции двух факторов выше 0,85, то один из них необходимо исключить из модели. Исследование матрицы коэффициентов корреляции позволяет сделать вывод, что в данную модель включены факторы, не очень тесно связанные между собой.
При изучении тесноты связи надо иметь в виду
, что величина коэффициентов корреляции является случайной, зависящей от объема выборки. Известно, что с уменьшением количества наблюдений надежность коэффициентов корреляции падает, и наоборот, при увеличении количества наблюдений надежность коэффициентов корреляции возрастает.
Значимость коэффициентов корреляции проверяется по критерию Стьюдента:
t =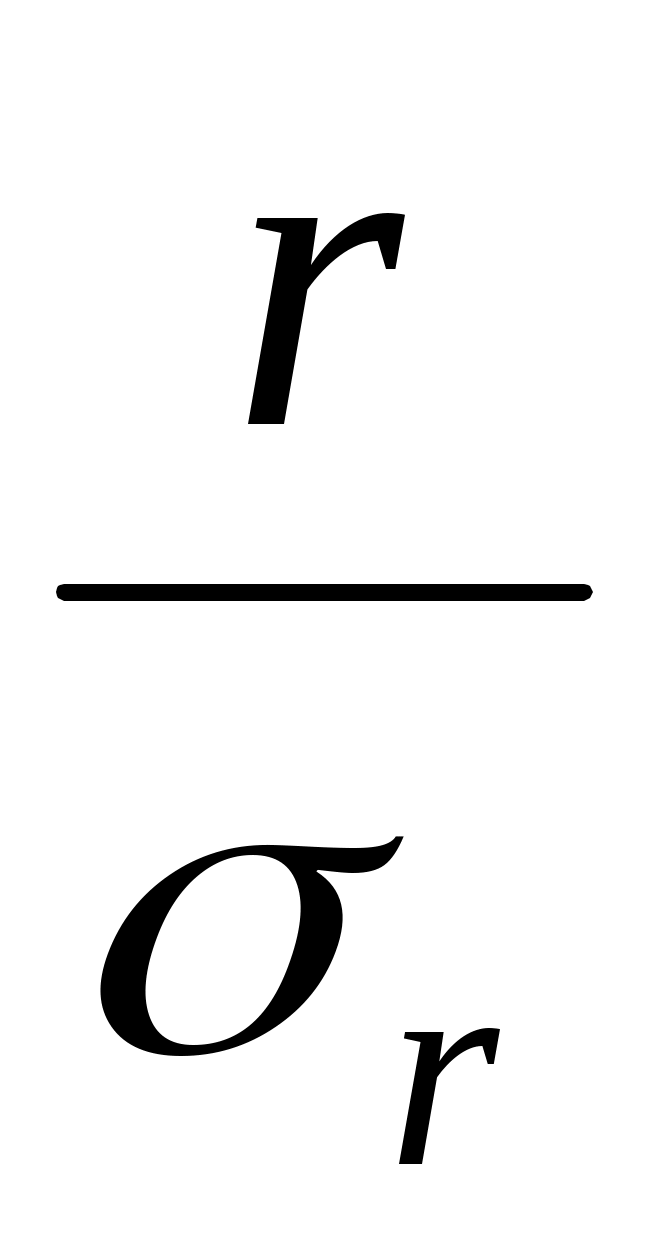
= 0,59 ∕ 0,103 = 5,72 (7.18)
где σr — среднеквадратическая ошибка коэффициента корреляции, которая определяется по формуле
σr =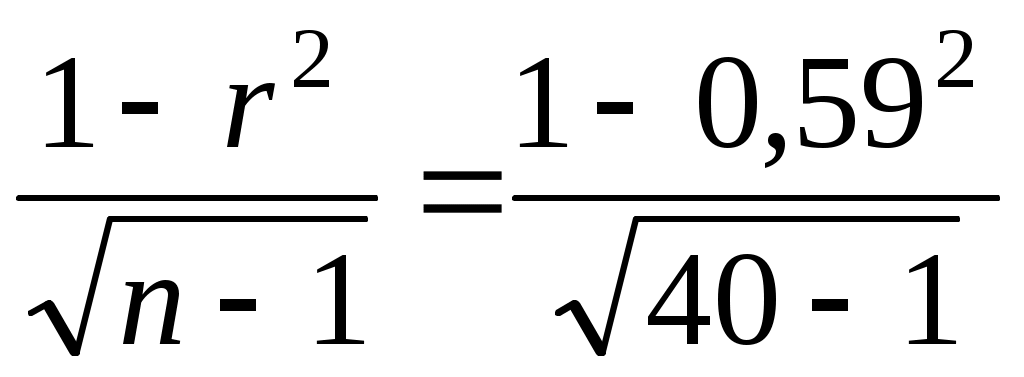
= 0,103. (7.19)
Если расчетное значение t выше табличного, то можно сделать заключение о том, что величина коэффициента корреляции является значимой. Табличные значения t находят по таблице значений критериев Стьюдента. При этом учитываются количество степеней свободы V = (n – 1) и уровень доверительной вероятности (в экономических расчетах обычно 0,05 или 0,01). В нашем примере количество степеней свободы равно n – 1 = 40 – 1 = 39. При уровне доверительной вероятности P = 0,05; t = 2,02. Поскольку t-фактическое (табл. 7.8)во всех случаях выше t-табличного, связь между результативным и факторными показателями является надежной, а величина коэффициентов корреляции — значимой.
Т а б л и ц а 7.8
Фактические значения критерия Стьюдента
Следующий этап корреляционного анализа — расчет уравнения связи (регрессии). Решение проводится обычно шаговым способом. Сначала в расчет принимается один фактор, который оказывает наиболее значимое влияние на результативный показатель, потом второй, третий и т.д. И на каждом шаге рассчитываются уравнение связи, множественный коэффициент корреляции и детерминации, F-отношение (критерий Фишера), стандартная ошибка и другие показатели, с помощью которых оценивается надежность уравнения связи. Величина их на каждом шаге сравнивается с предыдущей. Чем выше величина коэффициентов множественной корреляции, детерминации и критерия Фишера и чем ниже величина стандартной ошибки, тем
точнее уравнение связи описывает зависимости, сложившиеся между исследуемыми показателями. Если добавление следующих факторов не улучшает оценочных показателей связи, то надо их отбросить, т.е. остановиться на том уравнении, где эти показатели наиболее оптимальны.
Сравнивая результаты на каждом шаге (табл.7.9), мы можем сделать вывод, что наиболее полно описывает зависимости между изучаемыми показателями пятифакторная модель, полученная на пятом шаге. В результате уравнение связи имеет вид
Yх= 0,49 +3,65x1 +0,09x2 + 1,02x3 – 0,122x4 + 0,052x5.
Коэффициенты уравнения показывают количественное воздействие каждого фактора на результативный показатель при неизменности других. В данном случае можно дать следующую интерпретацию полученному уравнению: рентабельность повышается на 3,65 % при увеличении материалоотдачи на 1 руб.; на 0,09 % — с ростом фондоотдачи на 1 коп.; на 1,02 % — с повышением среднегодовой выработки продукции на одного работника на 1 тыс. руб.; на 0,052 % — при увеличении удельного веса продукции высшей категории качества на 1%. С увеличением продолжительности оборота средств на 1 день рентабельность снижается в среднем на 0,122 %.
Таблица 7.9
Результаты расчета уравнения связи
Коэффициенты регрессии в уравнении связи имеют разные единицы измерения, что делает их несопоставимыми, если возникает вопрос о сравнительной силе воздействия факторов на результативный показатель. Чтобы привести их в сопоставимый вид, все переменные уравнения регрессии выражают в долях среднеквадратического отклонения, другими словами, рассчитывают стандартизированные коэффициенты регрессии. Их еще называют бетта-коэффициентами по символу, который принят для их обозначения (β).
Бетта-коэффициенты и коэффициенты регрессии связаны следующим отношением:
βi =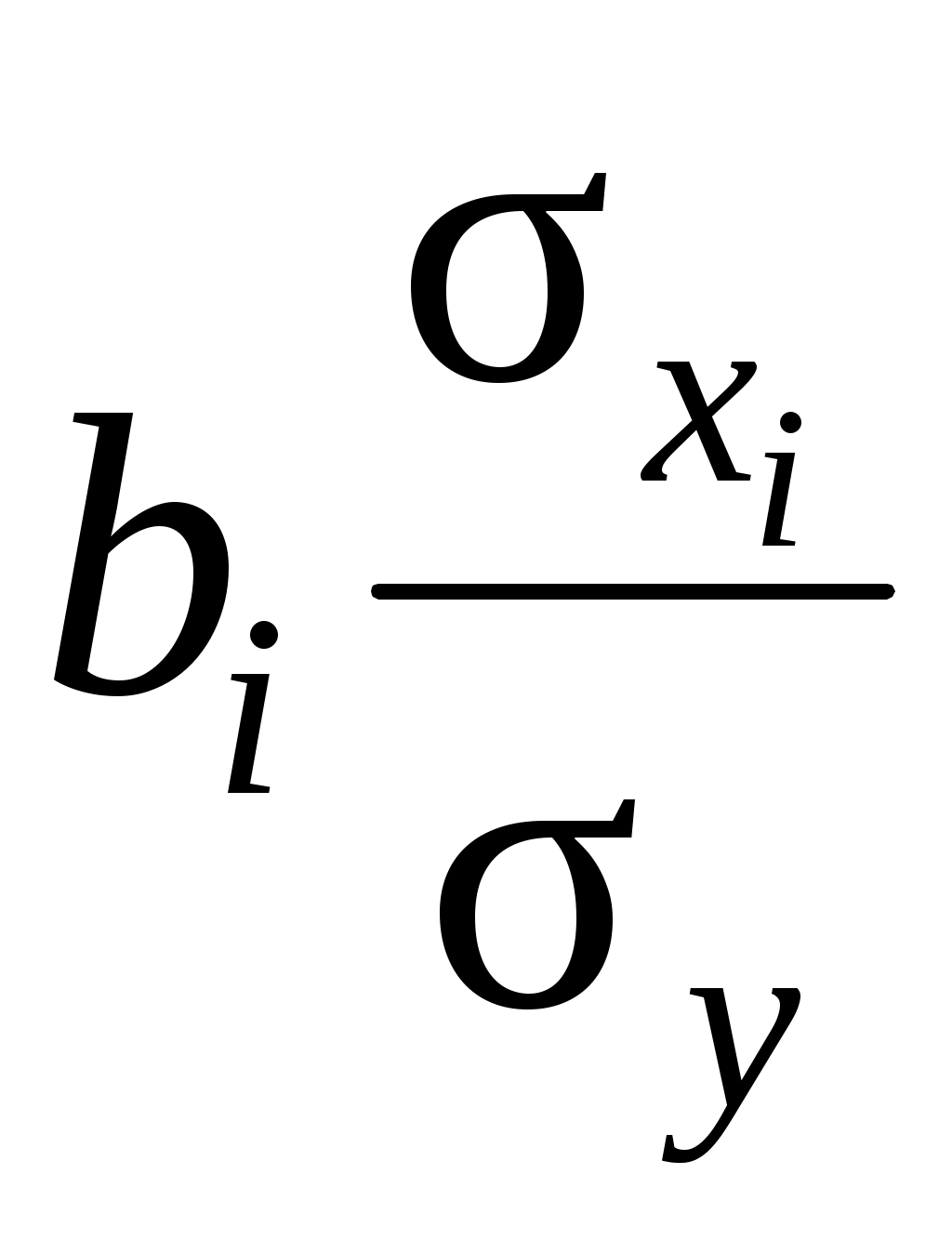
. (7.20)
Бетта-коэффициенты показывают, что если величина фактора увеличится на одно среднеквадратическое отклонение, то соответствующая зависимая переменная увеличится или уменьшится на долю своего среднеквадратического отклонения. Сопоставление бетта-коэффициентов позволяет сделать вывод сравнительной степени воздействия каждого фактора на величину результативного показателя. В нашем примере наибольшее влияние на уровень рентабельности оказывают материалоотдача, фондоотдача и производительность труда (табл. 7.10);
По аналогии можно сопоставить и коэффициенты эластичности, которые рассчитываются по формуле
Э =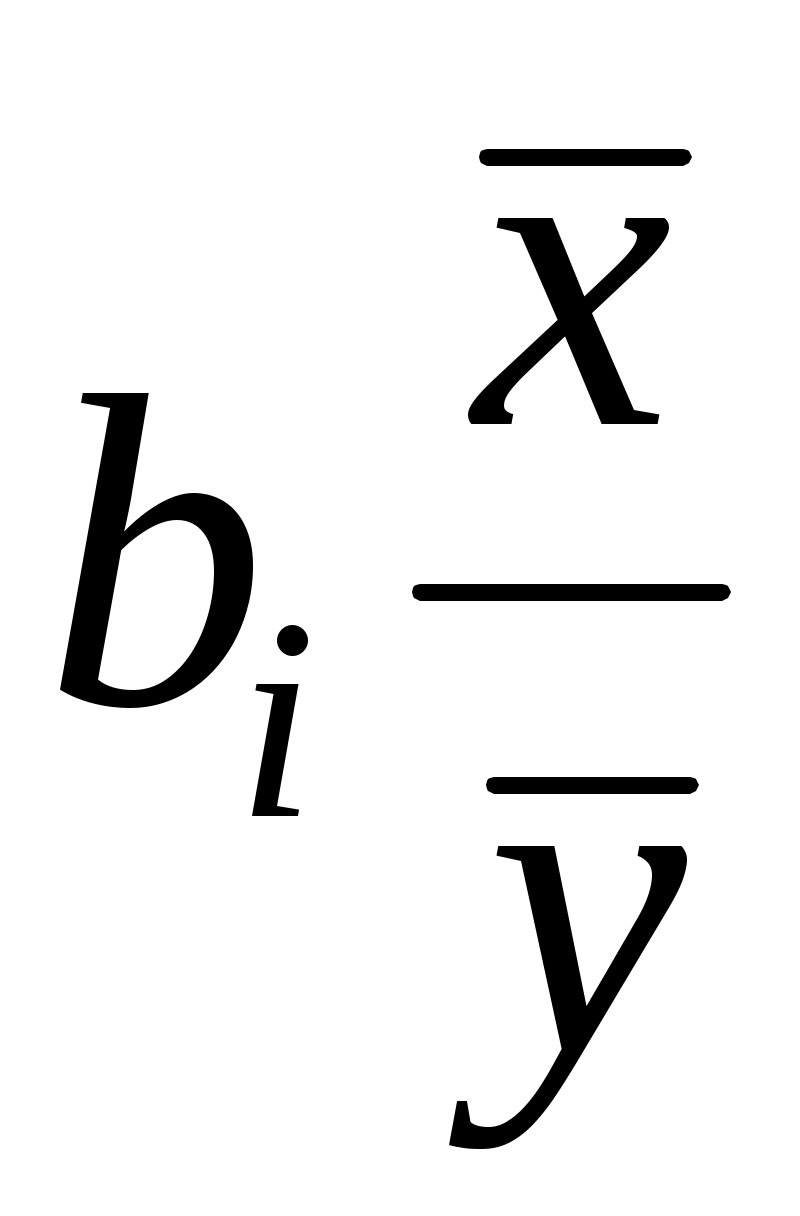
. (7.21
Коэффициенты эластичности показывают, на сколько процентов в среднем изменяется функция с изменением аргумента на 1%.
Т а б л и ц а 7.10
Коэффициенты эластичности и бетта-коэффициенты
Согласно данным табл. 7.10, рентабельность возрастает на 0,374% при увеличении уровня материалоотдачи на 1%, на 0,308% — при повышении фондоотдачи на 1% и т.д.
7.4. Методика оценки и практического применения результатов корреляционного анализа
Необходимость оценки уравнения связи. Показатели, которые применяются для оценки уравнения связи. Методика их расчета и интерпретация. Использование уравнения связи для оценки деятельности предприятия, определения влияния факторов на прирост результативного показателя подсчета резервов и планирования его уровня.
Для того чтобы убедиться в надежности уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для этого используются критерий Фишера (F-отношение), средняя ошибка аппроксимации коэффициенты множественной корреляции (R)и детерминации (D).
Критерий Фишера рассчитывается следующим образом:
F=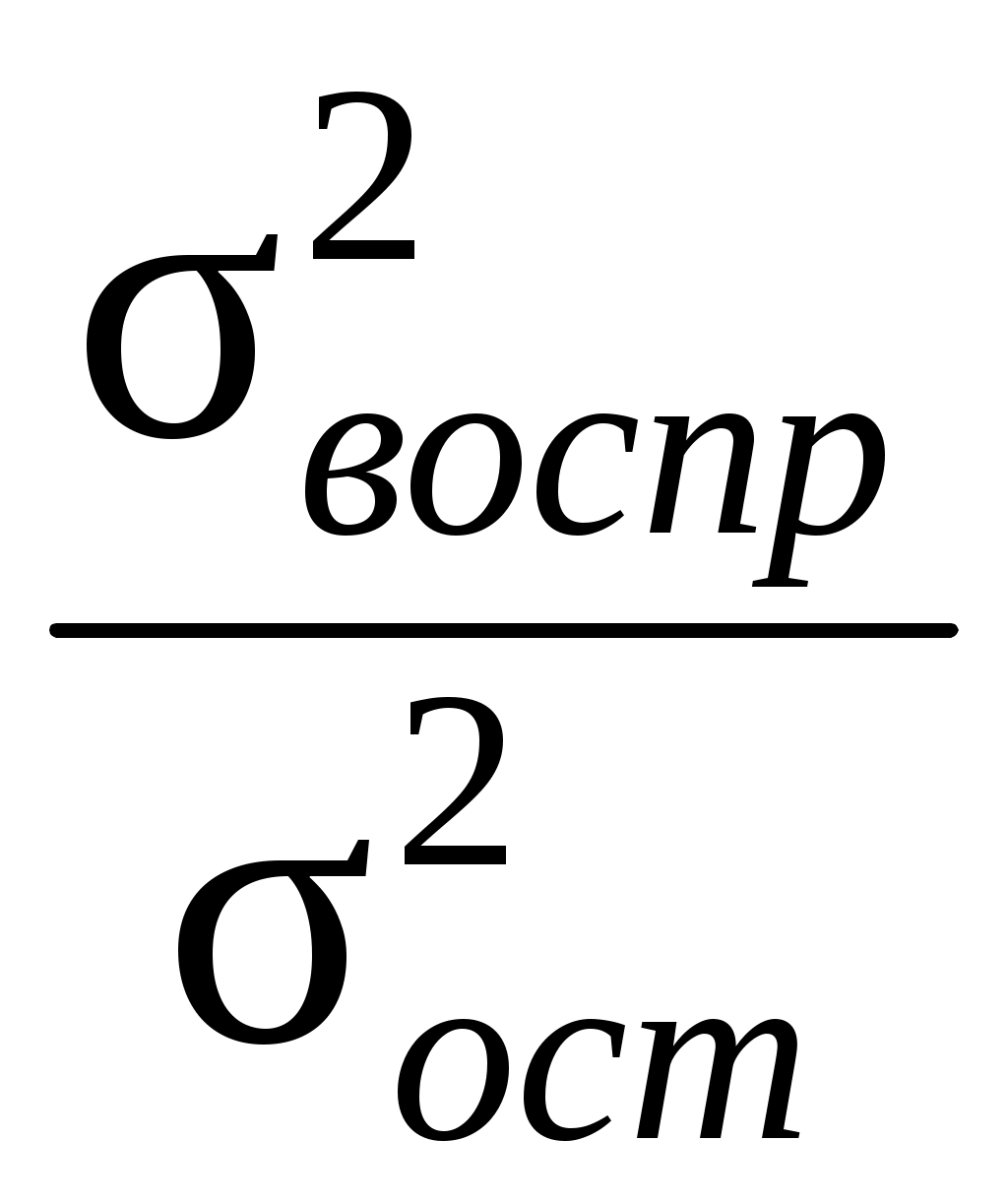
,
= 
; 
= 
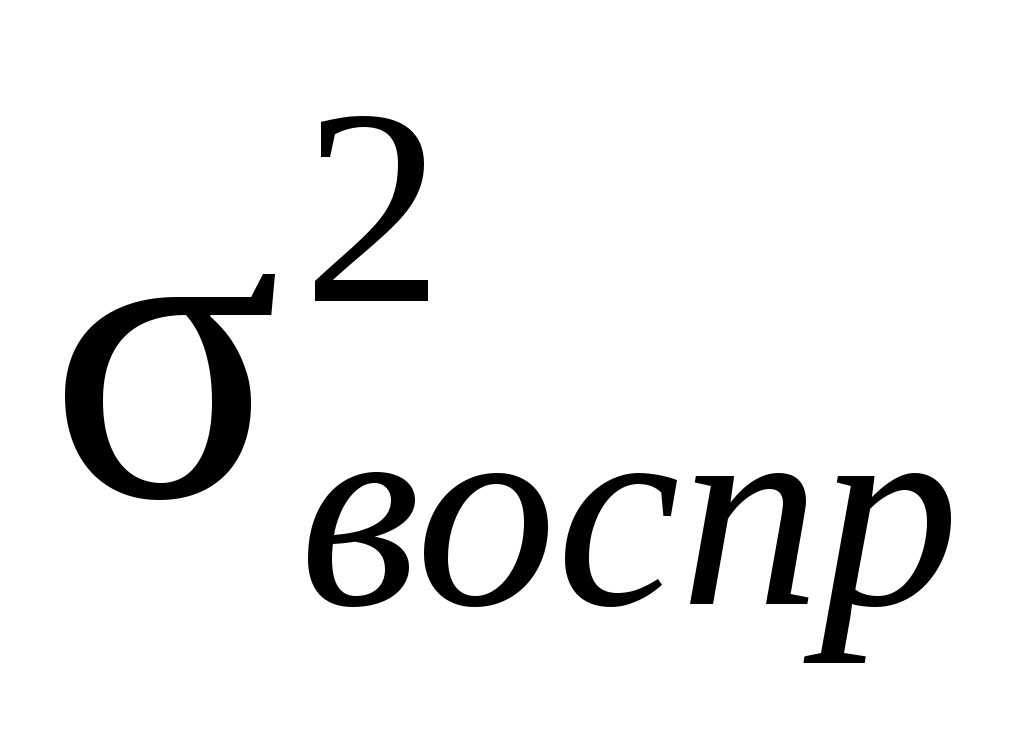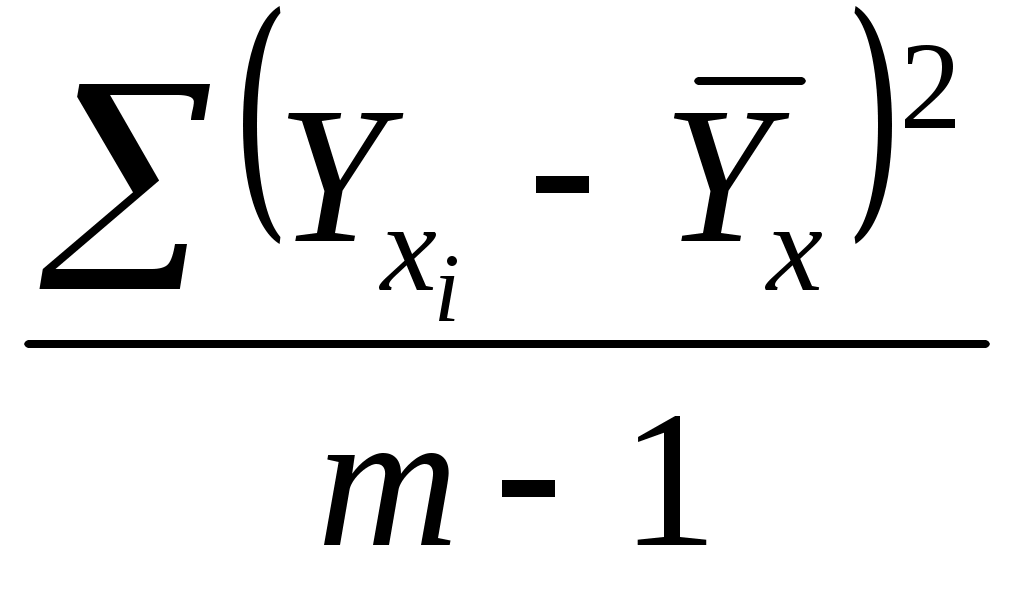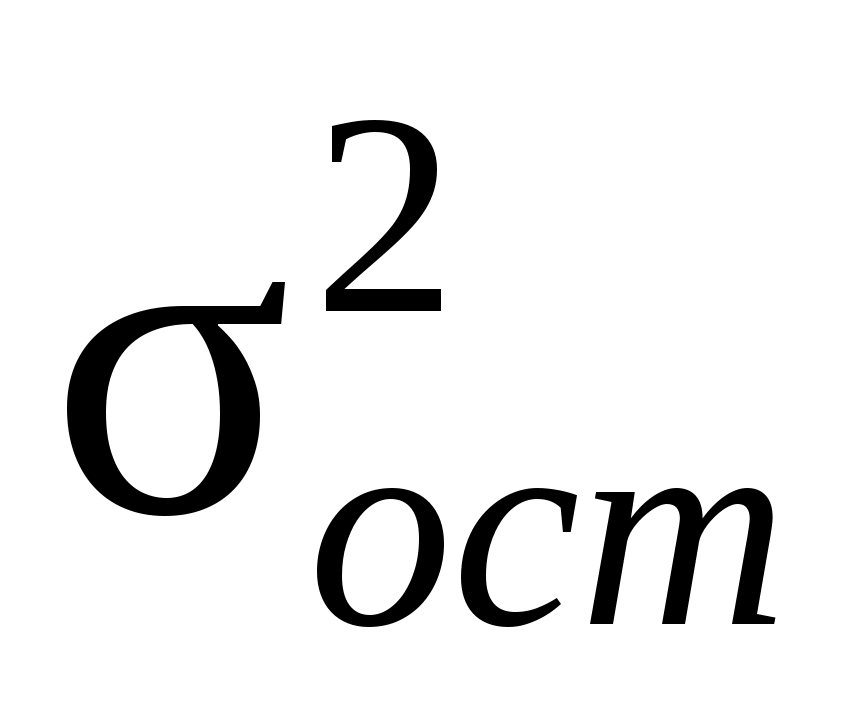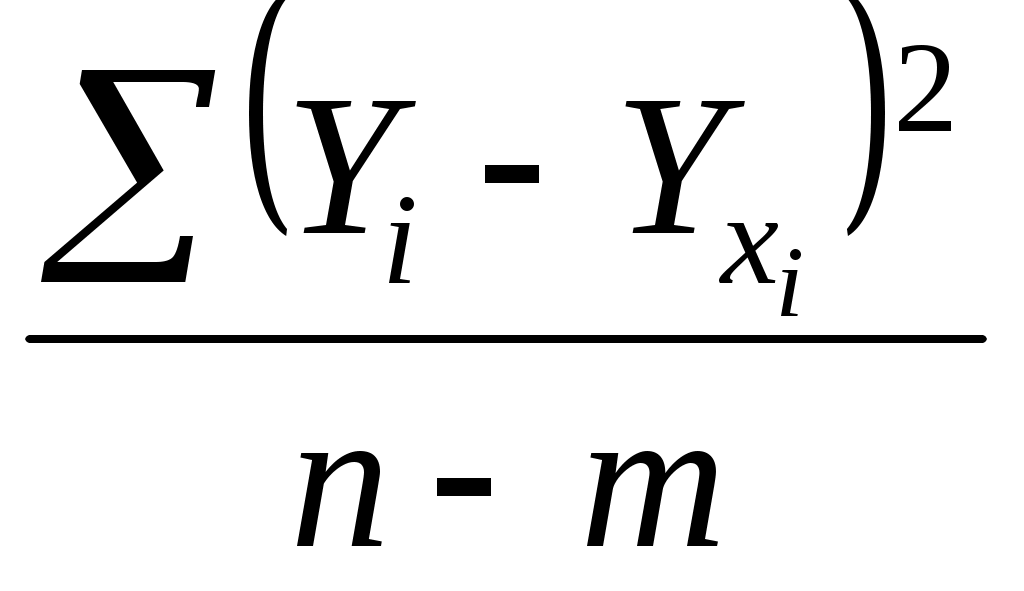; (7.22)
где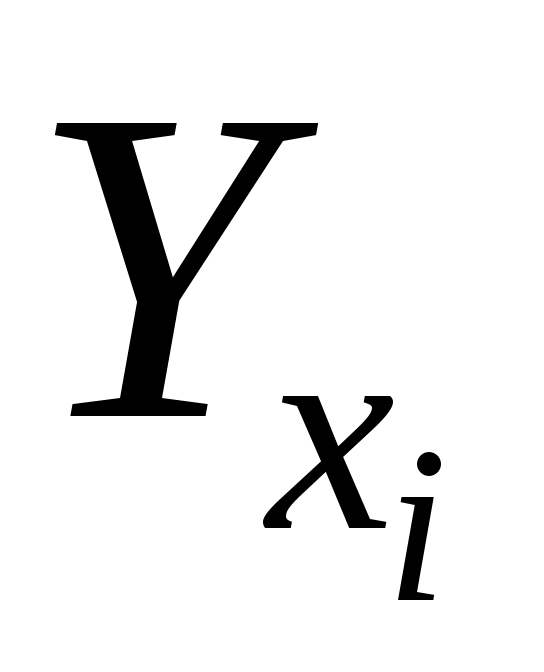
.— индивидуальные значения результативного показателя, рассчитанные по уравнению;
ух— среднее значение результативного показателя, рассчитанное по уравнению;
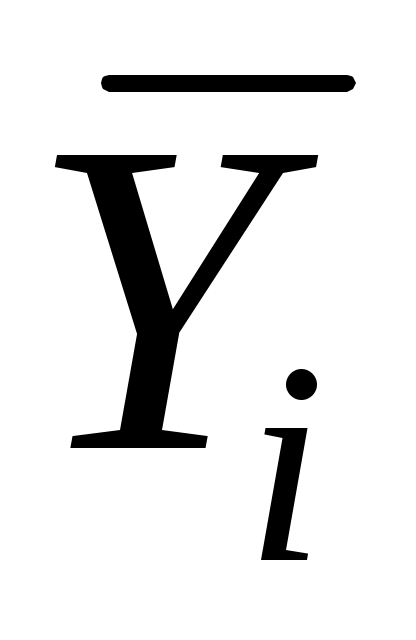— фактическиеиндивидуальные значения результативного показателя;
т — количество параметров в уравнении связи, учитывая свободный член уравнения;
п — количество наблюдений (объем выборки).
Фактическая величина F-отношения сопоставляется с табличной и делается заключение о надежности связи. В нашем примере величина F-отношения на пятом шаге равна 95,67.F-теоретическое рассчитано по таблице значений F. При уровне вероятности Р = 0,05 и количестве степеней свободы [(т - 1) = (6 – 1) = 5, (n – т ) = 40 – 6 = 34] оно будет составлять 2,49. Поскольку Fфакт > Fтабл , то гипотеза об отсутствии связи между рентабельностью и исследуемыми факторами отклоняется.
Для статистической оценки точности уравнения связи используется также
Т а б л и ц а 7.7
Матрица частных коэффициентов корреляции
| Показатель | y | x1 | x2 | x3 | x4 | x5 |
| y | 1 | | | | | |
| x1 | 0,59 | 1 | | | | |
| x2 | 0,48 | -0,136 | 1 | | | |
| x3 | 0,39 | 0,019 | 0,003 | 1 | | |
| x4 | -0,36 | 0,090 | -0,14 | -0,14 | 1 | |
| x5 | 0,31 | 0,098 | 0,16 | 0,48 | 0,082 | 1 |
Таким образом, с помощью парных и частных коэффициентов корреляции можно получить представление о тесноте связи между изучаемыми явлениями в общих и непосредственных соприкосновениях.
Значительный интерес представляют коэффициенты корреляции, характеризующие взаимосвязь факторов между собой. Как уже отмечалось, в корреляционную модель надо подбирать независимые между собой факторы. Если коэффициент корреляции двух факторов выше 0,85, то один из них необходимо исключить из модели. Исследование матрицы коэффициентов корреляции позволяет сделать вывод, что в данную модель включены факторы, не очень тесно связанные между собой.
При изучении тесноты связи надо иметь в виду
, что величина коэффициентов корреляции является случайной, зависящей от объема выборки. Известно, что с уменьшением количества наблюдений надежность коэффициентов корреляции падает, и наоборот, при увеличении количества наблюдений надежность коэффициентов корреляции возрастает.
Значимость коэффициентов корреляции проверяется по критерию Стьюдента:
t =
= 0,59 ∕ 0,103 = 5,72 (7.18)где σr — среднеквадратическая ошибка коэффициента корреляции, которая определяется по формуле
σr =
= 0,103. (7.19)Если расчетное значение t выше табличного, то можно сделать заключение о том, что величина коэффициента корреляции является значимой. Табличные значения t находят по таблице значений критериев Стьюдента. При этом учитываются количество степеней свободы V = (n – 1) и уровень доверительной вероятности (в экономических расчетах обычно 0,05 или 0,01). В нашем примере количество степеней свободы равно n – 1 = 40 – 1 = 39. При уровне доверительной вероятности P = 0,05; t = 2,02. Поскольку t-фактическое (табл. 7.8)во всех случаях выше t-табличного, связь между результативным и факторными показателями является надежной, а величина коэффициентов корреляции — значимой.
Т а б л и ц а 7.8
Фактические значения критерия Стьюдента
| Номер переменной | x1 | x2 | x3 | x4 | x5 |
| t-фактическое | 5,72 | 3,9 | 2,9 | 2,6 | 2,16 |
Следующий этап корреляционного анализа — расчет уравнения связи (регрессии). Решение проводится обычно шаговым способом. Сначала в расчет принимается один фактор, который оказывает наиболее значимое влияние на результативный показатель, потом второй, третий и т.д. И на каждом шаге рассчитываются уравнение связи, множественный коэффициент корреляции и детерминации, F-отношение (критерий Фишера), стандартная ошибка и другие показатели, с помощью которых оценивается надежность уравнения связи. Величина их на каждом шаге сравнивается с предыдущей. Чем выше величина коэффициентов множественной корреляции, детерминации и критерия Фишера и чем ниже величина стандартной ошибки, тем
точнее уравнение связи описывает зависимости, сложившиеся между исследуемыми показателями. Если добавление следующих факторов не улучшает оценочных показателей связи, то надо их отбросить, т.е. остановиться на том уравнении, где эти показатели наиболее оптимальны.
Сравнивая результаты на каждом шаге (табл.7.9), мы можем сделать вывод, что наиболее полно описывает зависимости между изучаемыми показателями пятифакторная модель, полученная на пятом шаге. В результате уравнение связи имеет вид
Yх= 0,49 +3,65x1 +0,09x2 + 1,02x3 – 0,122x4 + 0,052x5.
Коэффициенты уравнения показывают количественное воздействие каждого фактора на результативный показатель при неизменности других. В данном случае можно дать следующую интерпретацию полученному уравнению: рентабельность повышается на 3,65 % при увеличении материалоотдачи на 1 руб.; на 0,09 % — с ростом фондоотдачи на 1 коп.; на 1,02 % — с повышением среднегодовой выработки продукции на одного работника на 1 тыс. руб.; на 0,052 % — при увеличении удельного веса продукции высшей категории качества на 1%. С увеличением продолжительности оборота средств на 1 день рентабельность снижается в среднем на 0,122 %.
Таблица 7.9
Результаты расчета уравнения связи
| № п.п. | | Уравнение связи R | D | F | е |
| Шаг 1 (введен х1) | Yх= 5,81 + 7,68x1 | 0,59 | 0,35 | 50,3 | 1,895 |
| Шаг 2 (введен х2) | Yх= –1,11 + 5,12 x1 + 0,15 x2 | 0,75 | 0,56 | 57,6 | 1,548 |
| Шаг З (введен х3) | Yх= –6,84 + 3,93 x1 + 0,11х2 + l,53х3 | 0,84 | 0,72 | 71,3 | 1,408 |
| Шаг 4 (введен х4) | Yх= –2,44 + 3,89x1 + 0,10x2 + l,37x3 – 0,12x4 | 0,88 | 0,77 | 88,8 | 1,398 |
| Шаг 5 (введен х5) | Yх= 0,49 + 3,65x1 + 0,09х2 + 1,02x3 –0,122x4 + 0,052x5 | 0,92 | 0,85 | 95,67 | 1,358 |
Коэффициенты регрессии в уравнении связи имеют разные единицы измерения, что делает их несопоставимыми, если возникает вопрос о сравнительной силе воздействия факторов на результативный показатель. Чтобы привести их в сопоставимый вид, все переменные уравнения регрессии выражают в долях среднеквадратического отклонения, другими словами, рассчитывают стандартизированные коэффициенты регрессии. Их еще называют бетта-коэффициентами по символу, который принят для их обозначения (β).
Бетта-коэффициенты и коэффициенты регрессии связаны следующим отношением:
βi =
. (7.20)Бетта-коэффициенты показывают, что если величина фактора увеличится на одно среднеквадратическое отклонение, то соответствующая зависимая переменная увеличится или уменьшится на долю своего среднеквадратического отклонения. Сопоставление бетта-коэффициентов позволяет сделать вывод сравнительной степени воздействия каждого фактора на величину результативного показателя. В нашем примере наибольшее влияние на уровень рентабельности оказывают материалоотдача, фондоотдача и производительность труда (табл. 7.10);
По аналогии можно сопоставить и коэффициенты эластичности, которые рассчитываются по формуле
Э =
. (7.21Коэффициенты эластичности показывают, на сколько процентов в среднем изменяется функция с изменением аргумента на 1%.
Т а б л и ц а 7.10
Коэффициенты эластичности и бетта-коэффициенты
| Номер переменной | x1 | x2 | x3 | x4 | x5 |
| Коэффициент эластичности | 0,374 | 0,308 | 0,318 | -0,080 | 0,061 |
| Бетта-коэффициент | 0,359 | 0,275 | 0,213 | -0,118 | 0,133 |
Согласно данным табл. 7.10, рентабельность возрастает на 0,374% при увеличении уровня материалоотдачи на 1%, на 0,308% — при повышении фондоотдачи на 1% и т.д.
7.4. Методика оценки и практического применения результатов корреляционного анализа
Необходимость оценки уравнения связи. Показатели, которые применяются для оценки уравнения связи. Методика их расчета и интерпретация. Использование уравнения связи для оценки деятельности предприятия, определения влияния факторов на прирост результативного показателя подсчета резервов и планирования его уровня.
Для того чтобы убедиться в надежности уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для этого используются критерий Фишера (F-отношение), средняя ошибка аппроксимации коэффициенты множественной корреляции (R)и детерминации (D).
Критерий Фишера рассчитывается следующим образом:
F=
, = ; = ; (7.22)где
.— индивидуальные значения результативного показателя, рассчитанные по уравнению; ух— среднее значение результативного показателя, рассчитанное по уравнению;
— фактическиеиндивидуальные значения результативного показателя; т — количество параметров в уравнении связи, учитывая свободный член уравнения;
п — количество наблюдений (объем выборки).
Фактическая величина F-отношения сопоставляется с табличной и делается заключение о надежности связи. В нашем примере величина F-отношения на пятом шаге равна 95,67.F-теоретическое рассчитано по таблице значений F. При уровне вероятности Р = 0,05 и количестве степеней свободы [(т - 1) = (6 – 1) = 5, (n – т ) = 40 – 6 = 34] оно будет составлять 2,49. Поскольку Fфакт > Fтабл , то гипотеза об отсутствии связи между рентабельностью и исследуемыми факторами отклоняется.
Для статистической оценки точности уравнения связи используется также