Следующее требование к исходной информации — соответствие

---

ее закону нормального распределения. Согласно этому закону, основная масса исследуемых сведений по каждому показателю должна быть сгруппирована около ее среднего значения, а объекты с очень маленькими значениями или с очень большими должны встречаться как можно реже. График нормального распределения информации имеет следующий вид (рис. 7.1).



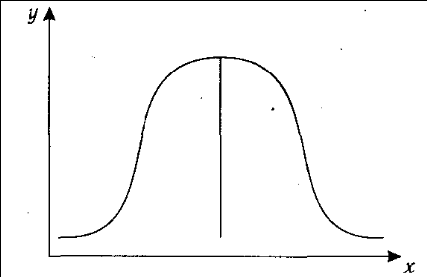
Рис. 7.1. График нормального распределения информации
Для количественной оценки степени отклонения информации от нормального распределения служит отношение показателя асимметрии к ее ошибке и отношение показателя эксцесса к его ошибке.

Показатель асимметрии (А)и его ошибка (т_а)рассчитываются по следующим формулам:

A = ; m_a= . (7.13)

Показатель эксцесса (Е)и его ошибка (т_е)рассчитываются следующим образом:

E = ; m_e= ; или m_e= 2m_a . (7.14)

В симметричном распределении А = 0. Отличие от нуля указывает на наличие асимметрии в распределении данных около средней величины. Отрицательная асимметрия свидетельствует о том, что преобладают данные с большими значениями, а с меньшими значениями встречаются значительно реже. Положительная асимметрия показывает, что чаще встречаются данные с небольшими значениями.

В нормальном распределении показатель эксцесса Е = 0. Если Е > 0, то данные густо сгруппированы около средней, образуя островершинность. Если Е < 0, то кривая распределения будет плосковершинной. Однако когда отношения А/m_аи Е/т_еменьше 3, то асимметрия и эксцесс не имеют существенного значения и исследуемая информация подчиняется закону нормального распределения.

В нашем примере (табл. 7.4) во всех случаях отношения А/m_аи Е/т_е не превышают 3. Значит, исходная информация соответствует этому закону.

После отбора факторов и оценки исходной информации важной задачей в корреляционном анализе является

---

моделирование связи между факторными и результативными показателями, т.е. подбор соответствующего уравнения, которое наилучшим образом описывает изучаемые зависимости.

Для его обоснования используются те же приемы, что и для установления наличия связи: аналитические группировки, линейные графики и др. Если связь всех факторных показателей с результативным носит прямолинейный характер, то для записи этих зависимостей можно использовать линейную функцию:

Y_х = а + b₁х₁ + b₂х₂ + b₃х₃+ ... + b_nх_n . (7.15)

Если связь между результативным и факторными показателями носит криволинейных характер, то может быть использована степенная функция:

Y_х = . (7.16)

или логарифмическая:

lgY_x = b₀ + b₁lg x₁ + b₂lg x₂ + … + b_nlg x_n. (7.17)

Приведенные модели выгодны тем, что их параметрам можно дать экономическое объяснение {интерпретацию). В линейной модели коэффициенты показывают, на сколько единиц изменяется результативный показатель с изменением факторного на единицу в абсолютном выражении, в степенных и логарифмических — в процентах.

В случаях, когда трудно обосновать форму зависимости, решение задачи можно провести по разным моделям и сравнить полученные результаты. Адекватность разных моделей фактическим зависимостям проверяется по критерию Фишера, показателю средней ошибки аппроксимации и величине множественного коэффициента детерминации, о которых речь пойдет несколько позже (см. § 7.4).

Изучение взаимосвязей между исследуемыми факторами и уровнем рентабельности показало, что все зависимости в нашем примере имеют прямолинейный характер. Поэтому для их описания использована линейная функция.

Решение задачи многофакторного корреляционного анализа проводится на ПЭВМ по типовым программам.

Сначала формируется матрица исходных данных (табл. 7.5), в первой колонке которой записывается порядковый номер наблюдения, во второй — результативный показатель (

---

у),а в следующих — факторные показатели (x_i).

Эти сведения вводятся в ПЭВМ и рассчитываются матрицы парных и частных коэффициентов корреляции, уравнение множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи: критерий Стьюдента, критерий Фишера, средняя ошибка аппроксимации, множественные коэффициенты корреляции и детерминации.

Т а б л и ц а 7.5

Исходные данные для корреляционного анализа

№ п.п.	y	x1	x2	x3	x4	x5
1	22,5	23,8	24,7	32,4	2,40	2,70
2	2,50	3,20	80,0	88,0	87,0	94,4
3	8,00	7,30	7,90	9,90	25,0	23,0
40	22,0	18,0	25,0	22,5	26,0	36,5

Изучая матрицы парных и частных коэффициентов корреляции, можно сделать вывод о тесноте связи между изучаемыми явлениями. Коэффициенты парной корреляции характеризуют тесноту связи между двумя показателями в общем виде с учетом взаимодействия с остальными факторами, определяющими уровень результативного показателя.

Данные табл. 7.6 (первый столбец) свидетельствуют о том, что все факторы оказывают ощутимое воздействие на уровень рентабельности. Особенно тесная связь рентабельности с материалоотдачей, фондоотдачей, качеством продукции и производительностью труда. С увеличением данных показателей уровень рентабельности повышается (прямая связь). При увеличении продолжительности оборота средств рентабельность снижается (обратная связь).

Матрица парных коэффициентов корреляции Т а б л и ц а 7.6

---

Показатель
y	1
x1	0,75	1
x2	0,73	0,34	1
x3	0,74	0,29	0,40	1
x4	-0,51	-0,33	-0,46	-0,45	1
x5	0,72	0,40	0,22	0,36	-0,37	1

Однако необходимо отметить, что парные коэффициенты корреляции получены при условии воздействия других факторов на результат. Чтобы абстрагироваться от их влияния и получить количественную характеристику связи между результативным и факторными показателями в чистом виде, рассчитываются частные коэффициенты корреляции (табл. 7.7).

При сравнении частных коэффициентов корреляции с парными видно, что влияние других факторов на тесноту связи между уровнем рентабельности и исследуемыми факторами довольно значимое: частные коэффициенты корреляции намного ниже парных. Это говорит о том, что факторы, которые входят в данную корреляционную модель, оказывают на рентабельность не только непосредственное влияние, но и косвенное. Поэтому взаимосвязи, очищенные от влияния сопутствующих факторов, получились менее тесными. В некоторых случаях они могут оказаться более тесными, если исключить влияние факторов, которые действуют в противоположном направлении. По этой причине может измениться не только величина коэффициента корреляции, но и направление связи: в общем виде связь может быть прямой, а в чистом — обратной, и наоборот. Объясняется это тем, что при расчете парных коэффициентов корреляции изучается взаимосвязь между результативным и факторным показателем с учетом их взаимодействия и с другими факторами. Например, с повышением уровня оплаты труда рентабельность увеличивается, если темпы роста производительности труда обгоняют темпы роста

---

Смотрите также файлы

• Устойчивость нелинейных систем. Особенности исследования устойчивости нелинейных сау.docx

• 1ВерноБаллов 1,00 из 1,00Отметить вопросТекст вопросаВ образовательных программах, ориентированных на достижение результатов определённого уровня, опыт самостоятельного .pdf

• Общее время решения 80 минут Теоретическая часть 1,4 балла за правильный ответ. Практическая часть, задачи 3,25 балла за правильный ответ.docx

• Тема 12. Кредитная политика Банка России. 12 Сущность и инструменты кредитной политики цб рф.docx

• Задача 1 Расчет лобовой врубки Рассчитать лобовую врубку, изображенную на рисунке, по исходным данным табл. 1.docx