Файл: Г. В. Савицкая Анализ хозяйственной деятельности предприятия.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 1247
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, как в связи с этим изменяются другие исследуемые показатели: возрастают или убывают, и в какой степени.
В табл. 4.7 приведены ранжированные данные об уровне урожайности сельскохозяйственных культур и качестве земли по 20 хозяйствам района. Из таблицы видно, что при повышении качества земли урожайность зерновых культур возрастает, и наоборот.
Таблица 4.7
Зависимость урожайности зерновых культур от качества земли
В экономическом анализе различают следующие виды сравнительного анализа: горизонтальный, вертикальный, трендовый, а также одномерный и многомерный.
Горизонтальный сравнительный анализ используется для определения абсолютных и относительных отклонений фактического уровня исследуемых показателей от базового (планового, прошлого периода, среднего уровня, достижений науки и передового опыта).
С помощью вертикального сравнительного анализа изучается структура экономических явлений и процессов путем расчета удельного веса частей в общем целом (удельный вес собственного капитала в общей его сумме), соотношение частей целого между собой (например, собственного и заемного капитала, основного и оборотного капитала), а также влияние факторов на уровень результативных показателей путем сравнения их величины до и после изменения соответствующего фактора.
Трендовый анализ применяется при изучении относительных темпов роста и прироста показателей за ряд лет к уровню базисного года, т.е. при исследовании рядов динамики.
При одномерном сравнительном анализе сопоставления делаются по одному или нескольким показателям одного объекта или нескольких объектов по одному показателю.
С помощью многомерного сравнительного анализа проводится сопоставление результатов деятельности нескольких предприятий (подразделений) по широкому спектру показателей. Подробнее его сущность рассмотрена в следующем параграфе.
4.2. Многомерные сравнения в анализе хозяйственной деятельности
Задачи, возможности и направления использования многомерных сравнений в АХД. Алгоритм многомерных сравнений.
Многомерный сравнительный анализ необходим для комплексной оценки результатов хозяйствования производственных подразделений, предприятий и т.д. Такая задача встает всегда, когда надо дать обобщающую рейтинговую оценку результатам хозяйствования нескольких предприятий. Это делают вышестоящие органы управления, а также инвесторы и банки для оценки степени финансового риска.
Обобщающая оценка результатов деятельности предприятий обычно проводится по целому комплексу показателей. В связи с этим задача обычно усложняется, поскольку субординация предприятий по разным показателям будет неодинаковой. Например, по объему производительности предприятие будет занимать первое место, по себестоимости — третье, а по уровню рентабельности — пятое и т.д.
Другое направление комплексной оценки — разработка алгоритмов вычислительных процедур, которые бы на основе комплекса показателей обеспечили однозначную оценку результатов хозяйственной деятельности.
Для решения этой задачи довольно широко используются алгоритмы расчета интегральных показателей, основанные на методах "суммы мест", геометрической средней и т.д. Но эти методики имеют существенный недостаток, потому что в них не учитываются весомость определенных показателей и степень различий в их уровне. Наиболее перспективным подходом является использование многомерного сравнительного анализа, основанного на методе эвклидовых расстояний, который позволяет учитывать не только абсолютные величины показателей каждого предприятия, но и степень их близости (дальности) до показателей предприятия-эталона. В связи с этим необходимо координаты сравниваемых предприятий выражать в долях соответствующих координат предприятия эталона, взятого за единицу.
Рассмотрим практическую сторону решения задачи многомерного сравнительного анализа.
Этап 1. Обосновывается система показателей, по которым будут оцениваться результаты хозяйственной деятельности предприятий, собираются данные по этим показателям и формируется матрица исходных данных (табл. 4.8). Исходные данные могут быть представлены как в виде моментных показателей, отражающих состояние предприятия на определенную дату, так и темповых показателей, характеризующих динамику деятельности предприятия и представленных в виде коэффициентов роста. Возможно изучение одновременно и моментных, и темповых показателей.
Этап 2. В табл. 4.8 в каждой графе определяется максимальный элемент, который принимается за единицу. Затем все элементы этой графы (аij) делятся на максимальный элемент эталонного предприятия (max аij). В результате создается матрица стандартизованных коэффициентов (xij), представленных в табл. 4.9:
xij =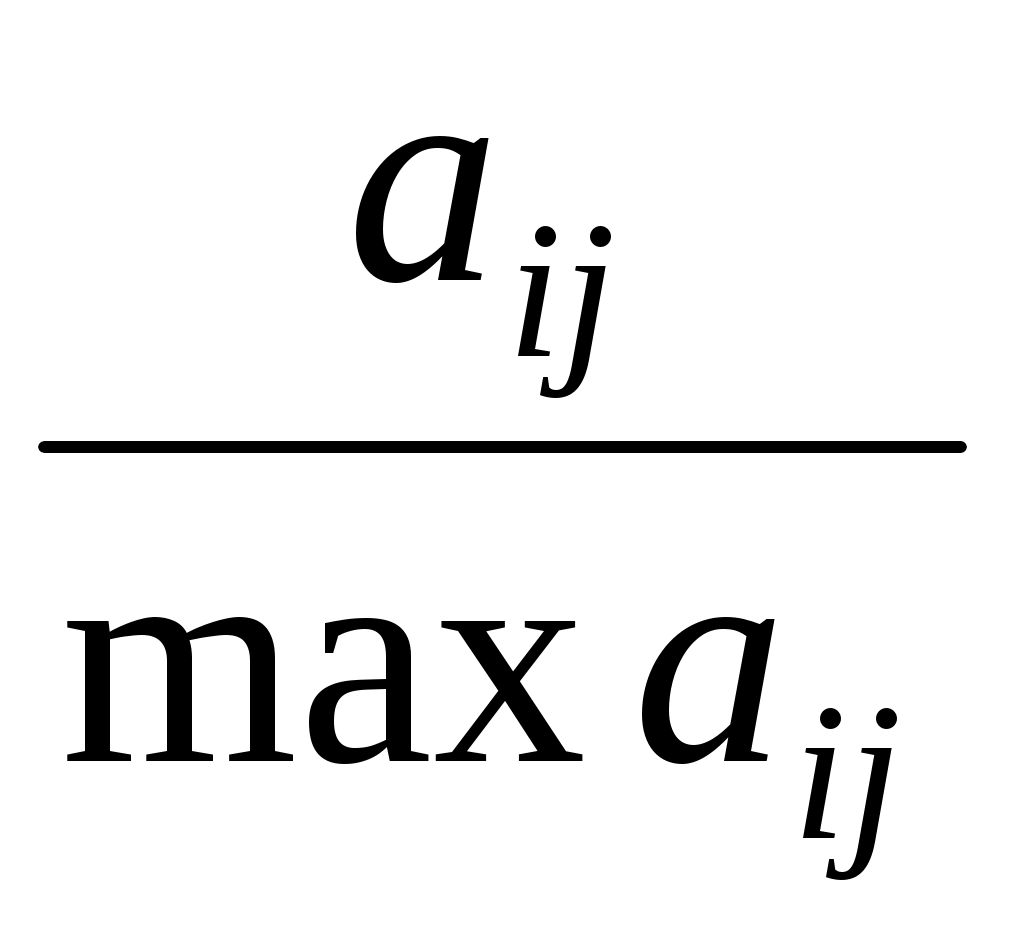
Таблица 4.8
Матрица исходных данных
Таблица 4.9
Матрица стандартизованных коэффициентов (xij)
Эталонное предприятие формируется обычно из совокупности однородных объектов, принадлежащих к одной отрасли. Однако это не исключает возможности выбора предприятия-эталона из совокупности предприятий, принадлежащих к различным отраслям деятельности, так как многие финансовые показатели сопоставимы и для разнородных субъектов хозяйствования.
Если с экономической стороны лучшим является минимальное значение показателя (например, затраты на рубль продукции), то надо изменить шкалу расчета так, чтобы наименьшему результату соответствовала наибольшая величина коэффициента.
Этап 3. Все элементы матрицы координат возводятся в квадрат. Если задача решается с учетом разного веса показателей, тогда полученные квадраты умножаются на величину соответствующих весовых коэффициентов (К),установленных экспертным путем, после чего результаты суммируются по строкам (табл. 4.10):
Rj =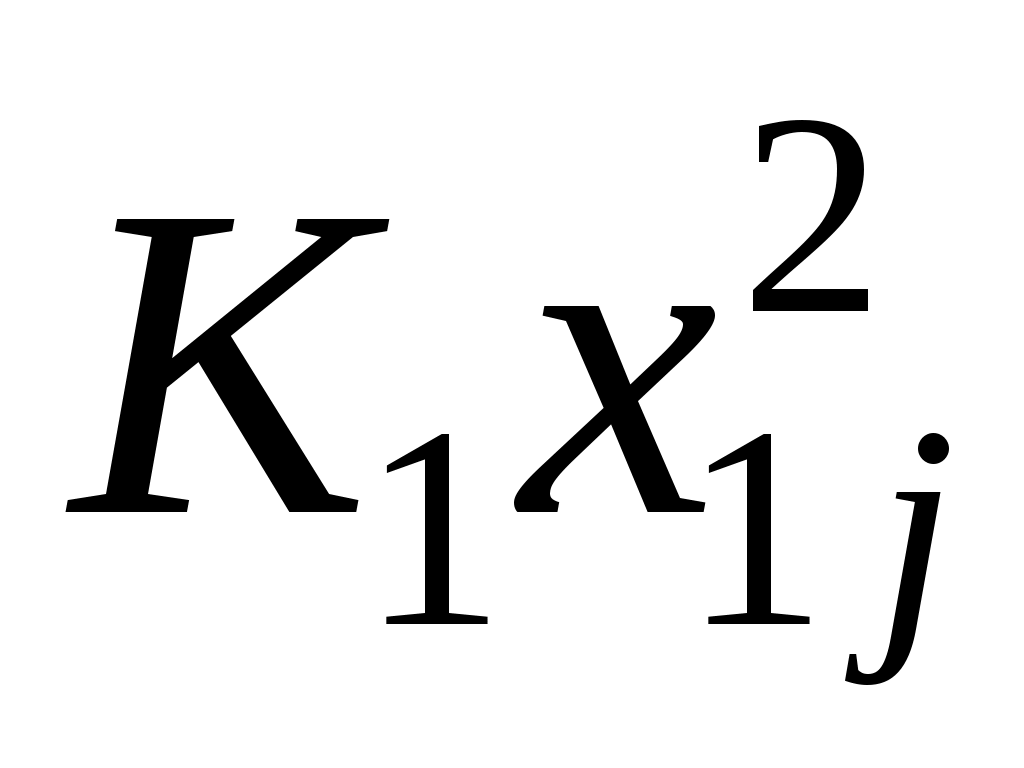 +
+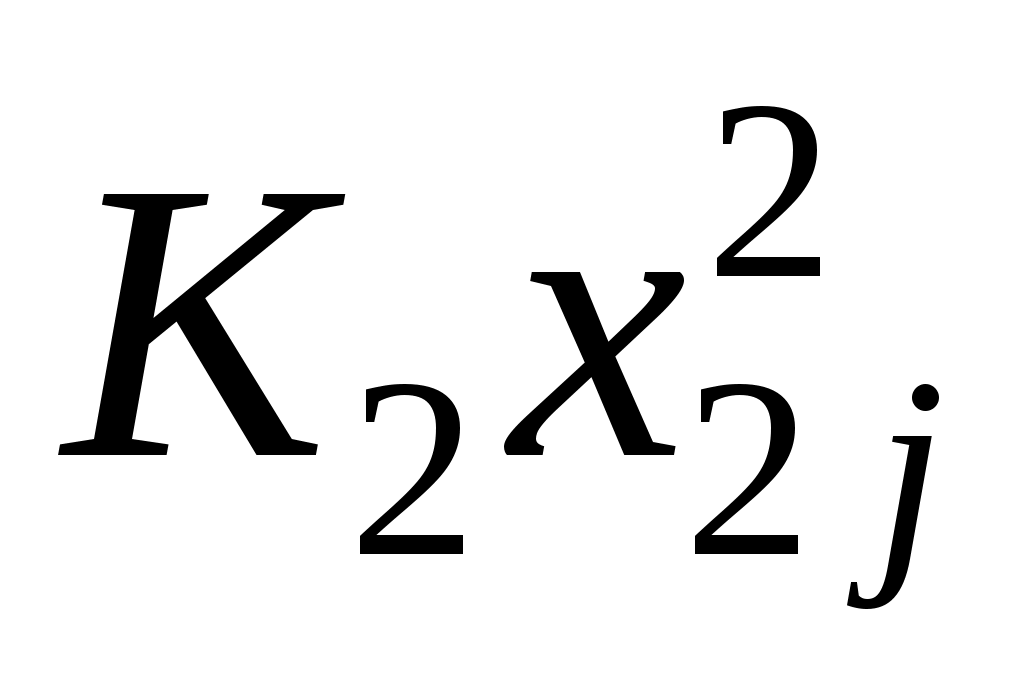
В табл. 4.7 приведены ранжированные данные об уровне урожайности сельскохозяйственных культур и качестве земли по 20 хозяйствам района. Из таблицы видно, что при повышении качества земли урожайность зерновых культур возрастает, и наоборот.
Таблица 4.7
Зависимость урожайности зерновых культур от качества земли
| Номер хозяйства | Качество земли, балл | Урожайность, ц/га | Номер хозяйства | Качество земли, балл | Урожайность, ц/га |
| 1 | 32 | 19,5 | 11 | 45 | 24,2 |
| 2 | 33 | 19,0 | 12 | 46 | 25,0 |
| 3 | 35 | 20,5 | 13 | 47 | 27,0 |
| 4 | 37 | 21,0 | 14 | 49 | 26,8 |
| 5 | 38 | 20,8 | 15 | 50 | 27,2 |
| 6 | 39 | 21,4 | 16 | 52 | 28,0 |
| 7 | 40 | 23,0 | 17 | 54 | 30,0 |
| 8 | 41 | 23,3 | 18 | 55 | 30,2 |
| 9 | 42 | 24,0 | 19 | 58 | 32,0 |
| 10 | 44 | 24,5 | 20 | 60 | 33,0 |
В экономическом анализе различают следующие виды сравнительного анализа: горизонтальный, вертикальный, трендовый, а также одномерный и многомерный.
Горизонтальный сравнительный анализ используется для определения абсолютных и относительных отклонений фактического уровня исследуемых показателей от базового (планового, прошлого периода, среднего уровня, достижений науки и передового опыта).
С помощью вертикального сравнительного анализа изучается структура экономических явлений и процессов путем расчета удельного веса частей в общем целом (удельный вес собственного капитала в общей его сумме), соотношение частей целого между собой (например, собственного и заемного капитала, основного и оборотного капитала), а также влияние факторов на уровень результативных показателей путем сравнения их величины до и после изменения соответствующего фактора.
Трендовый анализ применяется при изучении относительных темпов роста и прироста показателей за ряд лет к уровню базисного года, т.е. при исследовании рядов динамики.
При одномерном сравнительном анализе сопоставления делаются по одному или нескольким показателям одного объекта или нескольких объектов по одному показателю.
С помощью многомерного сравнительного анализа проводится сопоставление результатов деятельности нескольких предприятий (подразделений) по широкому спектру показателей. Подробнее его сущность рассмотрена в следующем параграфе.
4.2. Многомерные сравнения в анализе хозяйственной деятельности
Задачи, возможности и направления использования многомерных сравнений в АХД. Алгоритм многомерных сравнений.
Многомерный сравнительный анализ необходим для комплексной оценки результатов хозяйствования производственных подразделений, предприятий и т.д. Такая задача встает всегда, когда надо дать обобщающую рейтинговую оценку результатам хозяйствования нескольких предприятий. Это делают вышестоящие органы управления, а также инвесторы и банки для оценки степени финансового риска.
Обобщающая оценка результатов деятельности предприятий обычно проводится по целому комплексу показателей. В связи с этим задача обычно усложняется, поскольку субординация предприятий по разным показателям будет неодинаковой. Например, по объему производительности предприятие будет занимать первое место, по себестоимости — третье, а по уровню рентабельности — пятое и т.д.
Другое направление комплексной оценки — разработка алгоритмов вычислительных процедур, которые бы на основе комплекса показателей обеспечили однозначную оценку результатов хозяйственной деятельности.
Для решения этой задачи довольно широко используются алгоритмы расчета интегральных показателей, основанные на методах "суммы мест", геометрической средней и т.д. Но эти методики имеют существенный недостаток, потому что в них не учитываются весомость определенных показателей и степень различий в их уровне. Наиболее перспективным подходом является использование многомерного сравнительного анализа, основанного на методе эвклидовых расстояний, который позволяет учитывать не только абсолютные величины показателей каждого предприятия, но и степень их близости (дальности) до показателей предприятия-эталона. В связи с этим необходимо координаты сравниваемых предприятий выражать в долях соответствующих координат предприятия эталона, взятого за единицу.
Рассмотрим практическую сторону решения задачи многомерного сравнительного анализа.
Этап 1. Обосновывается система показателей, по которым будут оцениваться результаты хозяйственной деятельности предприятий, собираются данные по этим показателям и формируется матрица исходных данных (табл. 4.8). Исходные данные могут быть представлены как в виде моментных показателей, отражающих состояние предприятия на определенную дату, так и темповых показателей, характеризующих динамику деятельности предприятия и представленных в виде коэффициентов роста. Возможно изучение одновременно и моментных, и темповых показателей.
Этап 2. В табл. 4.8 в каждой графе определяется максимальный элемент, который принимается за единицу. Затем все элементы этой графы (аij) делятся на максимальный элемент эталонного предприятия (max аij). В результате создается матрица стандартизованных коэффициентов (xij), представленных в табл. 4.9:
xij =
Таблица 4.8
Матрица исходных данных
| Номер предприятия | Запас безубыточности, % | Коэффициент | Рентабельность, % | Коэффициент финансовой независимости | Доля собственного оборотного капитал в сумме текущих активов, % | ||
| ликвидности | оборачиваемости | продаж | капитала | ||||
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 30 | 1,8 | 3,2 | 25 | 22 | 0,75 | 16 |
| 2 | 25 | 2,0 | 2,5 | 30 | 26 | 0,62 | 26 |
| 3 | 52 | 1,5 | 2,8 | 35 | 25 | 0,55 | 25 |
| 4 | 40 | 1,7 | 2,2 | 33 | 38 | 0,68 | 30 |
| 5 | 22 | 1,4 | 2,7 | 24 | 16 | 0,58 | 0 |
| 6 | 30 | 1,6 | 3,5 | 20 | 21 | 0,72 | 35 |
| Весовой коэффициент | 2,0 | 1,0 | 1,5 | 1,2 | 1,8 | 1,3 | 1,6 |
Таблица 4.9
Матрица стандартизованных коэффициентов (xij)
| Номер предприятия | Показатель | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 0,577 | 0,90 | 0,914 | 0,714 | 0,579 | 1 | 0,457 |
| 2 | 0,481 | 1 | 0,714 | 0,857 | 0,684 | 0,826 | 0,743 |
| 3 | 1 | 0,75 | 0,800 | 1 | 0,658 | 0,733 | 0,714 |
| 4 | 0,769 | 0,85 | 0,628 | 0,943 | 1 | 0,907 | 0,857 |
| 5 | 0,423 | 0,70 | 0,771 | 0,686 | 0,421 | 0,773 | 0 |
| 6 | 0,577 | 0,80 | 1 | 0,571 | 0,553 | 0,960 | 1 |
Эталонное предприятие формируется обычно из совокупности однородных объектов, принадлежащих к одной отрасли. Однако это не исключает возможности выбора предприятия-эталона из совокупности предприятий, принадлежащих к различным отраслям деятельности, так как многие финансовые показатели сопоставимы и для разнородных субъектов хозяйствования.
Если с экономической стороны лучшим является минимальное значение показателя (например, затраты на рубль продукции), то надо изменить шкалу расчета так, чтобы наименьшему результату соответствовала наибольшая величина коэффициента.
Этап 3. Все элементы матрицы координат возводятся в квадрат. Если задача решается с учетом разного веса показателей, тогда полученные квадраты умножаются на величину соответствующих весовых коэффициентов (К),установленных экспертным путем, после чего результаты суммируются по строкам (табл. 4.10):
Rj =