(69.1)

Это отношение не зависит от л, так как с ростом rвыреза­емая конусом поверхность увеличивается пропорциональ­но r². Если r=1, то  численно равен , т. е. телесный угол измеряется поверхностью, вырезанной конусом на сфере единичного радиуса. Единицей телесного угла является стерадиан *) (ср) — телесный угол, которому на сфере еди­ничного радиуса соответствует поверхность с площадью, равной единице. Телесный угол, охватывающий все пространство вокруг источника, равен 4 ср, ибо площадь пол­ной поверхности сферы единичного радиуса есть 4.

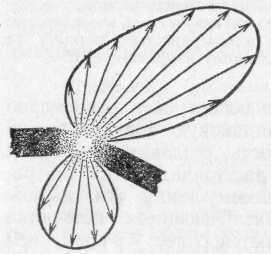
Полное излучение какого-либо источника распределяется в телесном угле 4 ср. Излучение называется равномерным или изотропным, если в одинаковые телесные углы, выде­ленные по любому направлению, излучается одинаковая мощность. Конечно, чем меньше телесные углы, в которых мы производим сравнение мощности, излучаемой источни­ком, тем с большей точностью мы проверяем равномерность излучения.

Итак, точенным источником является источник, размеры которого малы по сравнению с расстоянием до места наблюдения и который посылает световой поток равномерно во все стороны.

§ 70. Сила света и освещенность. Полный световой поток характеризует излучение, которое распространяется от

*) Стерадиан — пространственный радиан. Он, как видно из текста, определяется совершенно аналогично радиану, являющемуся единицей угла на плоскости.



Рис. 156. Телесный угол  ра­вен отношению площади поверх­ности , вырезанной на сфере конусом с вершиной в точке S, к квадрату радиуса r сферы: =/r²

источника по всем направлениям. Для практиче­ских же целей часто важнее знать не полный световой поток, а тот поток, который идет по определенному направле­нию или падает на определенную площадку. Так, например, автомобилисту важно получить достаточно большой све­товой поток в сравнительно узком телесном угле, внутри которого находится небольшой участок шоссе. Для работаю­щего за письменным столом важен тот поток, который осве­щает стол или даже часть стола, тетрадь или книгу, т. е. поток, приходящийся на некоторую площадь. В соответ­ствии с этим установлены два вспомогательных понятия —

---

сила света (I) и освещенность (Е).

Силой света называют световой поток, рассчитанный на телесный угол, равный стерадиану, т. е. отношение све­тового потока Ф, заключенного внутри телесного угла , к этому углу:

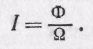(70.1)

Освещенность же есть световой поток, рассчитанный на единицу площади, т. е. отношение светового потока Ф, па­дающего на площадь а, к этой площади:

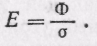(70.2)

Понятно, что формулы (70.1) и (70.2) определяют среднюю силу света и среднюю освещенность. Они будут тем ближе к истинным, чем равномернее поток или чем мень­ше  и .

Очевидно, что с помощью источника, посылающего оп­ределенный световой поток, мы можем осуществить весьма разнообразную силу света и весьма разнообразную осве­щенность. Действительно, если направить весь поток или большую его часть внутрь малого телесного угла, то в на­правлении, выделенном этим углом, можно получить очень большую силу света. Так, например, в прожекторах удается сосредоточить большую часть потока, посылаемого электрической дугой, в очень малом телесном угле и полу­чить в соответствующем направлении огромную силу света. В меньшей степени той же цели достигают с помощью авто­мобильных фар. Если сконцентрировать с помощью отража­телей или линз световой поток от какого-либо источника на небольшой площади, то можно достигнуть большой осве­щенности. Так поступают, например, стремясь сильно осве­тить препарат, рассматриваемый в микроскоп; аналогичное назначение выполняет рефлектор лампы, обеспечивающий хорошую освещенность рабочего места.

Согласно формуле (70.1) световой поток Ф равен произ­ведению силы света Iна телесный угол , в котором он рас­пространяется:



Если телесный угол =0, т. е. лучи строго парал­лельны, то световой поток также равен нулю. Это озна­чает, что строго параллельный пучок световых лучей не не­сет никакой энергии, т. е. не имеет физического смысла,— ни в одном реальном опыте не может быть осуществлен стро­го параллельный пучок. Это — чисто геометрическое поня­тие. Тем не менее параллельными пучками лучей очень ши­роко пользуются в оптике. Дело в том, что небольшие отступления от параллельности световых лучей, имеющие с энергетической точки зрения принципиальное значение, в вопросах, связанных с прохождением световых лучей че­рез оптические системы, практически не играют никакой роли. Например, углы, под которыми лучи от удаленной звезды попадают в наш глаз или телескоп, настолько малы, что они даже не могут быть измерены существующими ме­тодами; практически эти лучи не отличаются от параллель­ных. Однако эти углы все же не равны нулю, и именно бла­годаря этому мы и видим звезду. В последнее время свето­вые пучки с очень острой направленностью, т. е. с

---

очень малой расходимостью световых лучей, получают при помощи лазеров (см. § 205). Однако и в этом случае углы между лу­чами имеют конечное значение.

32. Законы освещенности.

Законы освещенности. Как показывают формулы (70.1) и (70.2), величины Е и I связаны между собой.

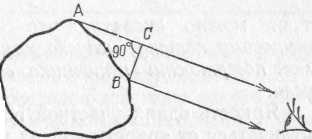
Пусть точечный источник S освещает небольшую пло­щадку , расположенную на расстоянии Rот источника (рис. 157).

Построим телесный угол , вершина которого лежит в точке Sи который опирается на края площадки . Он равен /R². Поток, посылаемый источником в этот телесный угол, обозначим через Ф. Тогда сила света I=Ф/=Ф•R²/, ос­вещенность E=Ф/. Отсюда

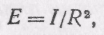(71.1)

т. е. освещенность площадки равна силе света, деленной на квадрат расстояния до точечного источника. Сравнивая освещенности площадок, расположенных на разных расстояниях R₁,R₂от точечного источника, найдем E₁=I/R²₁, E₂=I/R²₂и т. д., или

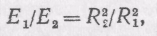(71.2)

т. е. освещенность обратно пропорциональна квадрату рас­стояния от площадки до точечного источника. Это так назы­ваемый закон обратных квад­ратов.

Если бы площадка а была расположена не перпендику­лярно к оси потока, а поверну­та на угол а, то она имела бы размеры =₀cos (рис. 158), где ₀ — площадка, пересе­кающая тот же телесный угол перпендикулярно к оси пуч­ка, так что =₀/R².Мы предполагаем площадки и ₀ настолько малыми и столь удаленными от источника, что

для всех точек этих площадок расстояние до источника мо­жет считаться одинаковым (R) и лучи во всех точках состав­ляют с перпендикуляром к площадке один и тот же угол  (угол падения).



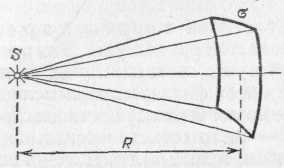
Рис. 157. Освещенность площад­ки , перпендикулярной к оси светового потока, определяется силой света и расстоянием

---

R от точечного источника S до пло­щадки



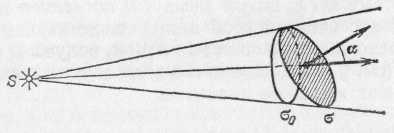
Рис. 158. Освещенность площадки  пропорциональна косинусу угла , образуемого перпендикуляром к площадке с направлением светово­го потока

В таком случае освещенность площадки есть

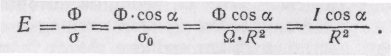(71.3)

Итак, освещенность, создаваемая точечным источником на некоторой площадке, равна силе света, умноженной на ко­синус угла падения света на площадку и деленной на квад­рат расстояния до источника.

Закон обратных квадратов соблюдается вполне строго для точечных источников. Если же размеры источника не очень малы по сравнению с расстоянием до освещаемой поверхности, то соотношение (71.1) не верно и освещен­ность убывает медленнее, чем по закону 1/R²;в частности, если размеры светящейся поверхности велики по сравнению с R, то освещенность практически не меняется при измене­нии R. Чем меньше размеры источника dпо сравнению с R, тем лучше выполняется закон обратных квадратов. Так,

при соотношении d/R1/10 расчеты изменения освещенности

по формуле (71.1) дают вполне хорошее согласие с наблю­дением. Таким образом, закон обратных квадратов можно считать практически выполняющимся, если размеры источ­ника не превышают 0,1 расстояния до освещаемой поверхности.

Освещенность поверхности, как видно из формулы (71.3), зависит, кроме того, от угла, под которым падают на эту [поверхность световые лучи.

---

§ 72. Единицы световых величин. В системе световых еди­ниц за исходную величину принята единица силы света. Эта единица имеет условный характер: в качестве единицы силы света принята сила света некоторого эталон­ного источника. Таким источником, дающим силу света I=1, вначале условились считать пламя свечи, изготовлен­ной строго стандартным образом. Однако этот эталонный источник оказался мало удобным, так как даваемая им сила света несколько изменяется по мере образования «нагара» и, кроме того, зависит от температуры и влажности воздуха. Для установления эталона силы света было предложено много других источников, в частности эталонные электрические лампы накаливания, образцы которых хранятся в крупных государственных измерительных лабораториях и контролируются взаимными сравнениями.

Единица силы света называется канделой (кд) — от ла­тинского слова candela, что означает свеча. Кандела равна силе света в заданном направлении источника, испускаю­щего излучение частоты 540•10¹² Гц (длина волны в вакууме 555 нм), энергетическая сила света которого в этом на­правлении составляет 1/683 Вт/ср. Кандела является одной из основных единиц Международной системы единиц (СИ).

Эталоны в виде электрических ламп не являются достаточно постоянными я в случае их порчи не могут быть точно воспроизведены. Поэтому международным соглашением введен новый эталон, который можно точно воспроизвести. Он представляет собой специально устроен­ный сосуд, в котором расплавляется химически чистая платина; в платину вставлена тугоплавкая узкая трубочка, раскаляемая до температуры платины. Свет испускается внутренней полостью трубочки через ее открытый конец. При затвердевании чистой платины температура ее имеет строго определенное значение, равное 2042 К. Сила света, излу­чаемого при этой температуре в направлении оси трубочки с поверхно­сти, равной 1/60 см², будет строго определенной. Эта сила света равна одной канделе.

За единицу светового потока принят лю­мен (обозначается лм). Люмен есть световой поток, испус­каемый точечным источником, сила света которого равна 1 кд, внутри единичного телесного угла (т. е. угла, равного 1 ср). Для излучения, соответствующего максимуму спект­ральной чувствительности глаза (=555 нм), световой по­ток равен 683 люменам, если энергетическая сила света рав­на 1 Вт/ср.

За единицу освещенности принимается ос­вещенность такой поверхности, на 1 м² которой падает све­товой поток 1 лм, равномерно распределенный по площадке. Эта единица освещенности называется люкс (лк). Освещен­ность 1 лк получается на поверхности сферы радиуса 1 м, если в центре сферы помещен точечный источник, сила света которого равна 1 кд. Приведем значения освещенности для некоторых типичных случаев (табл. 1).

Таблица 1. Освещенность (в люксах) в некоторых типичных случаях



С открытием лазеров, обладающих высокой интенсив­ностью, появилась возможность создавать значительно боль­шие освещенности, правда, в течение очень малых проме­жутков времени. Существенную роль играет то свойство лазеров, что они дают излучение с малой расходимостью светового пучка. Благодаря этому все излучение лазера практически можно собрать в пятнышко с площадью около 10^-6 см². Небольшой лазер с полной энергией 0,1 Дж за вспышку, длящуюся 10^-8 с, создает в пределах такого пят­нышка в течение вспышки «чудовищно» большую плотность мощности 10¹³ Вт/см² или 10 тераватт/см² (ТВт/см²) *). За­метим, что мощность всех электростанций на Земле состав­ляет примерно 1 ТВт. Легко подсчитать, что освещенность, создаваемая таким лазером в пределах небольшого пятныш­ка, для света с длиной волны =555 нм составляет при­мерно 10³⁰ лк, т. е. почти в 10¹⁵ раз выше, чем максимальная освещенность, даваемая Солнцем.

33. Яркость источников и освещенных поверхностей.

Яркость источников. До сих пор мы рассматривали только точечные источники света. В действительности источники обычно являются протяженными, т. е. рассматривая их с заданного расстояния, мы различа­ем их форму и размеры. Для характеристики протяженных источников, да­ре в том простейшем случае, когда они представля­ют собой равномерно светящиеся шарики, недоста­точно одной только величи­ны— силы света. Действи­тельно, представим себе два светящихся шарика, испускающих свет равномерно во все стороны и имеющих одинаковую силу света, но разный диаметр. Освещенность, создаваемая каждым из этих шариков на одинаковом расстоянии от их центра, будет одинакова. Однако по своему виду эти шарики будут представлять сильно различающиеся источники света: маленький шарик оказывается более ярким, чем большой. Это происходит вследствие того, что при одинаковой силе света излучающая поверхность одного шарика больше, чем второго, и, следовательно, сила света, испускаемого с единицы площади источ­ника, в том и другом случаях различна. Отметим, что когда мы рассматриваем какой-либо источник света, для нас имеет значение не площадь самой излучающей поверхности, а размеры видимой поверхности, т. е. проекции излучающей поверхности на плоскость, перпендикулярную к направлению наблюдения (рис. 159).

Итак, мы приходим к выводу, что для характеристики 'свойств протяженного источника света нужно знать силу



Рис. 159. Соотношение между дейст­вительной излучающей поверхностью (АВ) и поверхностью, видимой по данному направлению (ВС)

*) Приставка тера образована от греческого слова «терас» — чу­довище.

света, рассчитанную на единицу площади видимой поверх­ности источника. Эта световая величина называется яр­костью источника; мы будем ее обозначать буквой L. Если источник имеет силу света I и площадь видимой светящейся поверхности его есть , то яркость этого источника равна

(73.1)

Пользуясь формулой (70.1), имеем также

(73.2)

т. е. можно сказать, что яркость источника равна световому потоку, испускаемому с единицы площади види­мой поверхности источника внутри единичного телесного угла.

Яркость одних участков поверхности источника может отличаться от яркости других участков. Например, различ­ные участки пламени свечи, лампы и т, п. имеют сильно различающиеся яркости. Кро­ме того, яркость зависит от направления, в котором про­исходит излучение источни­ка. Это связано с тем, что си­ла света многих источников зависит от направления. На­пример, электрическая дуга по некоторым направлениям совсем не посылает света (рис. 160).

Итак, яркость может слу­жить для характеристики из­лучения какого-либо участка поверхности источника в за­данном направлении. Вместе с тем яркость имеет большое значение в силу того, что, как мы увидим ниже, это — та световая величина, на которую непосредственно реагирует глаз.

Единицей яркости является кандела на квадратный метр. Такой яркостью обладает светящаяся площадка, дающая с каждого квадратного метра силу света, равную 1 кд в направлении, перпендикулярном к пло­щадке.

Характеристики яркости различных светящихся тел приведены в табл. 2.



Рис. 160. Яркость электричес­кой дуги, пропорциональная дли­не стрелок на рисунке, зависит от направления излучения

Таблица 2. Яркость некоторых источников света (в кд/м²)



Источники света с большой яркостью (свыше 1 ,6•10⁵ кд/м²) вызывают болезненное ощущение в глазу. Для того чтобы глаз не подвергался действию яркого света источников, применяют различные приспособления. Так, например, рассматривание раскаленной спирали лампы на­каливания вредно и даже болезненно для глаза. Если же колба лампочки сделана из матового или молочного стекла или прикрыта арматурой в виде матового шара, то излучае­мый ею световой поток исходит с большей поверхности. Бла­годаря этому яркость падает, тогда как световой поток прак­тически не изменяется и, следовательно, освещенность, соз­даваемая лампой, также остается неизменной.

Яркость освещенных поверхностей. Экраны кинотеат­ров и аудиторий, окрашенные потолки, стены, декорации и т. д. представляют собой диффузно отражающие поверх­ности.

Такого рода поверхности при освещении играют роль протяженных источников с большими поверхностями и обычно с умеренной яркостью. В этом смысле они удачно дополняют мало протяженные самосветящиеся источники (лампы накаливания, газосветные лампы, свечи и т. п.), которые обычно обладают небольшими поверхностями и большими яркостями.

Яркость такой освещенной поверхности будет, очевидно, пропорциональна ее освещенности. Действитель­но, чем больше освещенность, т. е. чем бо'льший световой поток падает на единицу поверхности, тем больше будет и поток, отраженный этой поверхностью, а следовательно, и яркость освещенной поверхности.

Яркость освещенной поверхности будет, кроме того, тем больше, чем больше ее альбедо, т. е. чем большая часть падающего на поверх­ность потока рассеивается ею. Таким образом, яркость освещенной по­верхности Lдолжна быть пропорциональна произведению освещенности Е на альбедо , т. е. L



---

Смотрите также файлы

• Скарлатина острое инфекционное заболевание, вызываемое гемолитическим стрептококком группы а (бгса) (син. S. pyogenes) и сопровождающееся характерной сыпью. А38. Скарлатина. Эпидемиология.docx

• Не установлено сокращение.docx

• Прочитайте ситуации из опыта работы волонтеров (добровольцев). Какой вид компетентности необходим для того, чтобы справляться с описанными проблемами.odt

• Байау тжірибесі Орындаан Аманжанова Аякз штб203.pptx

• Задание Составьте опорную схему с комментариями на тему Функции педагогической деятельности. Задание 2.docx