Файл: Отчет по учебной практике Череповецкий государственный университет.docx

2) если уравнение имеет вид ax² + bx = 0, то используется метод факторизации: x (ax + b) = 0; т.е. либо x = 0, либо ax + b = 0. Результатом являются два корня: x1 = 0; х2 = -b/2;

3) Если уравнение имеет вид ах2 + с = 0, то преобразовать его к виду ах² = - с и затем х²=-c/a. В случае –c/a <0, уравнение x² = -c/a не имеет корней (следовательно, у него нет корней и исходное уравнение ax² + c = 0). В случае –c/a> 0, т.е. –c/a= m, где m>0, уравнение x² = m имеет два корня x₁= , x₂ = - , (в этом случае допустима более короткая запись x_1,2 = .

Таким образом, неполное квадратное уравнение может иметь два корня, один корень и не иметь корней.

На втором этапе происходит переход к решению полного квадратного уравнения. Это уравнения вида ax² + bx + c = 0, где a, b, c — заданные числа, a ≠ 0, x — неизвестное.

Любое полное квадратное уравнение можно привести к виду

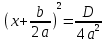, определить количество корней квадратного уравнения и найти эти корни. Рассмотрены следующие случаи решения полных квадратных уравнений: D < 0, D = 0, D > 0.

1. Если D < 0, то квадратное уравнение ax² + bx + c = 0 не имеет действительных корней.

Например, 2x² + 4x + 7 = 0. Решение: здесь a = 2, b = 4, c = 7.

Д = b² - 4ас = 42 - 4 * 2 * 7 = 16 - 56 = - 40.

Поскольку D <0, это квадратное уравнение не имеет корней.

2. Если D = 0, то квадратное уравнение ax² + bx + c = 0 имеет корень, находящийся по формуле .

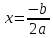Например 4x² - 20x + 25 = 0. Решение: a = 4, b = - 20, c = 25.

D = b² - 4ас = (-20) 2 - 4 * 4 * 25 = 400 - 400 = 0.

Поскольку D = 0, это уравнение имеет корень. Этот корень находится по формуле 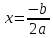. Получаем ,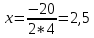

3. Если D > 0, то квадратное уравнение ax² + bx + c = 0 имеет два корня, которые находятся по формулам:

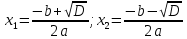
Например 3x² + 8x - 11 = 0. Решение: a = 3, b = 8, c = -11. D = b² - 4ас = 82 - 4 * 3 * (-11) = 64 + 132 = 196.

Поскольку D > 0, это квадратное уравнение имеет два корня. Эти корни находятся по формулам:

---

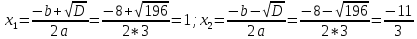
Составляется алгоритм решения уравнения вида ax² + bx + c = 0.

1. 
   Вычислите дискриминант D по формуле D = b² - 4ac.
   

2. Если D < 0, то квадратное уравнение ax² + bx + c = 0 не имеет корней.

3. Если D = 0, то квадратное уравнение имеет корень, находящийся по формуле

4. Если D > 0, то квадратное уравнение ax² + bx + c = 0 имеет два корня: .

Этот алгоритм универсален, он применим как к неполным, так и к полным квадратным уравнениям. Однако неполные квадратные уравнения обычно не решаются этим алгоритмом.

Таким образом, мы можем заключить, что квадратные уравнения могут быть решены в деталях с использованием сформулированного выше правила. [1.98].

На третьем этапе рассматриваются редуцированные квадратные уравнения, имеющие вид x² + px + q = 0 (3), где p и q — числа. Число p — это коэффициент при x, а q — свободный член. Дискриминант уравнения:

D = p² - 4q. Рассматриваются 3 случая:

1. 
   D> 0, то уравнение имеет два корня, вычисляемых по формуле.
   

2. 
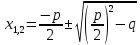
   D = 0, то уравнение (3) имеет один корень, или, как говорят, два совпадающих корня:
   

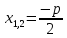
3. D <0, то уравнение не имеет корней. Обычно в случае редуцированного квадратного уравнения вместо D рассматривается выражение 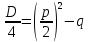, который имеет тот же знак, что и D. В этом случае формула для корней приведенного квадратного уравнения записывается следующим образом: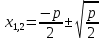

Следует:

1. 
   Когда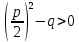 тогда уравнение имеет два корня;
   
2. 
   Когда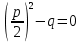 тогда уравнение имеет два совпадающих корня;
   
3. 
   Когда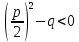 то уравнение не имеет корней.
   

Важным моментом при изучении квадратных уравнений является рассмотрение теоремы Виета, утверждающей существование связи между корнями и коэффициентами редуцированного квадратного уравнения.

---

Теорема Виета. Сумма корней данного квадратного уравнения равна второму коэффициенту, взятому с обратным знаком, а произведение корней равно свободному члену.

Другими словами, если x₁ и x₂ — корни уравнения x² + px + q = 0, то

х₁ + х₂ = - р,

х₁ х₂ = q

Эти формулы называются формулами Виета в честь французского математика Ф. Виета (1540—1603), введшего систему алгебраических символов и разработавшего основы элементарной алгебры. Он одним из первых начал обозначать числа буквами, что значительно продвинуло теорию уравнений.

Например, приведенное выше уравнение х² - 7х +10 = 0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. Видно, что сумма корней равна второму коэффициенту, при обратном взятом знаке и произведение корней равно свободному члену.

Существует также теорема, противоположная теореме Виета.

Обратная теорема Виета. Если формулы

х₁ + х₂ = - р,

х₁ х₂ = q

верны для чисел x₁, x₂, p, q, то x₁ и x₂ являются корнями уравнения

x² + px + q = 0 [2.49].

Теорема Виета и обратная к ней теорема широко используются для решения различных задач.

Пример.

Запишем заданное квадратное уравнение, корнями которого являются числа 1 и -3.

По формулам Виета

– р = х¹ + х² = - 2,

q = х¹ х² = -3.

Следовательно, искомое уравнение имеет вид x² + 2x - 3 = 0.

Сложность усвоения теоремы Виета связана с несколькими обстоятельствами. Во-первых, необходимо учитывать разницу между прямыми и обратными предложениями. В прямой теореме Виета дано квадратное уравнение и его корни; наоборот, чисел всего два, а квадратное уравнение стоит в конце теоремы. Студенты часто делают ошибку, подкрепляя свои аргументы неправильной ссылкой на прямую или обратную теорему Виета.

Например, при нахождении корней квадратного уравнения методом подбора необходимо обращаться к обратной теореме Виета, а не к прямой, как это часто делают студенты. Чтобы распространить теоремы Виета на случай нулевого дискриминанта, мы должны согласиться с тем, что в этом случае квадратное уравнение имеет два равных корня. Удобство такого соглашения проявляется в факторизации квадратного трехчлена

Так, неполные и редуцированные квадратные уравнения имеют разные алгоритмы решения; при изучении этого предмета необходимо показать, что общая формула корня применима к этим случаям. Обычно их исследуют перед выводом корней общего квадратного уравнения. В целом можно сказать, что овладение темой «Квадратные уравнения» поднимает учащихся на качественно новый уровень овладения содержанием школьной математики.

---

Урок на тему "Формула корней квадратного уравнения с четным вторым коэффициентом"

Цели:

• 
  научить детей решать квадратные уравнения с новой формулой;
  
• 
  повторить ранее изученный материал по теме «Квадратные уравнения»;
  
• 
  Развивать у детей счет, внимание, память и математический язык;
  
• 
  Воспитывать аккуратность, умение аргументировать свою точку зрения.
  

Оборудование: карточки с формулами.

Во время урока

1. Домашнее задание.

- Откройте дневники, запишите домашнее задание: выучите формулы, вывод этих формул.

2. Устные упражнения.

- В начале урока повторяем теоретический материал по теме: «Квадратные уравнения».

Фронтальный опрос

1. Что называется квадратным уравнением? (Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a, b, c — любые действительные числа и a ≠ 0).

2. В уравнении 2х+4х²+1=0 (на доске).

- Наименование: - Старший коэффициент (4);

- второй коэффициент (2)

- свободный срок (1).

3. Какое уравнение называется приведенным квадратным уравнением? Пример. (Квадратное уравнение называется приведенным, если старший коэффициент равен 1. Пример: x² + 3x + 4 = 0).

4. Какое уравнение называется полным квадратным уравнением? (Полное квадратное уравнение — это уравнение, в котором присутствуют все три члена, т. е. уравнение, в котором b, c ≠ 0).

5. Какое уравнение называют неполным квадратным уравнением? (Неполное квадратное уравнение — это уравнение, в котором присутствуют не все три члена.)

6. Что вы называете корнем квадратного уравнения? (Корнем квадратного уравнения является любое значение переменной x, при котором квадратный трехчлен ax² + bx + c = 0 обращается в нуль; такое значение переменной x называется корнем квадратного трехчлена).

7. Что значит решить квадратное уравнение? (Итак, найдите все его корни или установите, что корней нет).

3. Сообщение темы и цели урока.

- А теперь познакомимся с еще одной формулой, которая поможет вам найти корни квадратного уравнения.

- Мы научимся применять его при решении квадратных уравнений.

Работа по теме урока

Историческая справка.

- Решать простые уравнения люди научились более 3 тысяч лет назад в Древнем Египте, в Вавилоне, и только 400 лет назад научились решать квадратные уравнения. Одним из тех, кто внес крупный вклад в развитие математики, был французский математик Виет. Формы для решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые описаны в «Книге счетов», написанной в 1202 г. итальянским математиком Леонардом Фибоначчи. Автор самостоятельно разработал несколько новых алгебраических примеров для решения задач и первым в Европе подошел к введению отрицательных чисел.

---

Объяснение нового материала.

- Записываем сегодняшнюю дату и тему нашего урока в лекционных тетрадях: «Формула корней квадратного уравнения с четным вторым коэффициентом».

- Все внимательно слушаем, в блокнот пока ничего не пишем.

Напишите слова учителя на доске.

1. Квадратное уравнение ax² + bx + c = 0

ax² + bx + c = 0, для второго четного b = 2n. коэффициент, т.е. b = 2n.

- Тогда уравнение ax² + 2nx + c = 0 можно записать так:

- Найдите дискриминант (вместо b D = (2n) ² - 4ac = напишем 2n).

- Что у тебя?

- Что я могу сделать с этим выражением? = 4n² - 4ас =

(открытые скобки)

- Что случится?

- И тогда можно поставить 4 за скобки. = 4(n2 - ас)

- Выражение в скобках обозначается через n² – ac = D₁

- Запишите мои записи с доски в тетрадь.

2. - От чего зависит количество корней в D = 4 (n² - ас) = 4D₁

квадратное уравнение? (от значения D).

- От чего зависит значение D? (от значения D₁)

- Пусть D> 0, тогда D₁> 0 и D = 4D₁> 0 D₁> 0


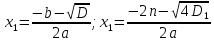
- Чему равно D? (4D₁)

- Что можно сделать дальше? (Давайте вынесем 2 под знаком корня).

- Что еще мы можем сделать? (вынести общий множитель за скобки и сократить)
- Кто может записать, чему равно х₂.


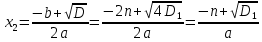
Микрообобщение: так, если



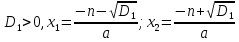
- Напишите в тетради, как мы нашли х₁ и х₂.

3. Если D₁=0, то D=0.

Сколько корней имеет квадратное уравнение? (1 корень).

По какой формуле его найти?

- так как b = 2n, заменить вместо b → 2n.

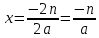
Итак, если D₁ = 0, то

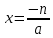
- Запиши это в тетрадь!

4. Если D₁ < 0, то D< 0

Что вы знаете о корнях? (корней нет)

5. Рассмотрим эту формулу для x² + 2nx + c = 0 редуцированного квадратного уравнения.

Какова формула квадратных корней мы получаем?



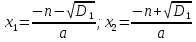
а = 1.

- Запиши это!

- Посмотри внимательно, какие вопросы у тебя есть?

Итог: Мы познакомились с новой формулой, которая частично облегчает наши расчеты

---