Лабораторная работа №7 «Построение математической модели продуктивного пласта на основе метода множественной регрессии»

Пусть имеется два поля, два вида каротажа опорной скважины (F₁; F₂).

Введем функцию Y, отражающую гипотезу Н₀ о продуктивном пласте вдоль эталонного объекта. Это значит, что:



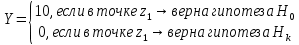
Матрицы F и Y будет иметь следующий вид:

F1	F2	Y
10,373	6,76	0
4,373	9,373	0
13,373	7,373	0
15,373	-13,627	0
14,373	-10,627	0
13,373	-12,627	0
6,76	-7,627	0
6,76	-6,627	0
5,76	-6,627	0
11,76	-13,627	0
9,76	-6,627	0
7,76	0,76	0
5,76	-1,24	0
11,28	5,72	0
-6,28	6,72	0
-8,28	22,72	10
-16,28	11,72	10
-15,28	12,72	10
-14,28	14,72	10
-11,72	12,72	10
-14,28	10,72	10
-9,4	7,4	0
12,373	-0,24	0
18,373	3,76	0
10,373	-5,627	0
8,373	-10,627	0
9,373	-9,627	0
7,373	-11,627	0
15,373	-7,627	0
4,76	1,76	0
7,76	-0,24	0
9,76	2,76	0
0,76	2,76	0
-0,24	2,76	0
14,373	1,76	0
14,373	-10,62	0
13,373	-12,27	0
6,76	-7,67	0
2,73	-6,62	0
5,76	-6,67	0

---

Будем полагать, что между полем Y и полями F₁ и F₂ существует линейная корреляционная зависимость:



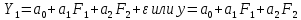
Отыщем уравнение, определяющее связь значений функции Y со значениями геологических полей F₁ и F₂ в каждой точке скважины.

В матричном виде эта зависимость примет вид:



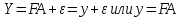
где 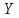– заданные значения функции, а 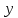- вычисленные значения по уравнению регрессии у=FA.

Задача состоит в нахождении коэффициентов А,



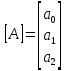
Для решения системы уравнений наберем следующее выражение:



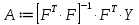
Для начала к матрице с переменными Fj добавляем единичный столбец. Получим матрицу :

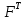1	1	1	1	1	…	1	1	1	1
10,373	4,373	13,373	15,373	14,373	…	13,373	6,76	2,73	5,76
6,76	9,373	7,373	-13,627	-10,627	…	-12,27	-7,67	-6,62	-6,67

Умножим матрицы (F^T·F):

40	202,818	-23,735
202,818	4650,147	-2554,3
-23,735	-2554,3	3349,515

Умножим матрицы F^T и Y:

60

-801,2

853,2

---

????^???? ∙ ???? =

Находим обратную матрицу ^[????^???? ∙ ????^]−1:

0,036758	-0,00251	-0,00166
-0,00251	0,000542	0,000395
-0,00166	0,000395	0,000588

^[????^???? ∙ ????^]−1 =


Далее и находим коэффициенты А по ранее известной формуле:

???? ≔ ^[????^???? ∙ ????^]−1 ∙ ????^???? ∙ ????

0,036758	-0,00251	-0,00166
-0,00251	0,000542	0,000395
-0,00166	0,000395	0,000588

60

-801,2

853,2

2,806

-0,24753

0,085847

???? =


В результате получим вектор-столбец искомых коэффициентов А.

Полученные на эталонном объекте значения коэффициентов 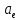позволяют записать уравнение

---

регрессии,

???? = 2,806 - 0,24753 · ????₁ + 0,085847 · ????₂

с помощью которого по заданным значениям полей F₁ и F₂ по скважине можно вычислить и построить регрессионную модель продуктивного пласта.

x	y
1	0,818749
2	2,528219
3	0,128797
4	-2,16904
5	-1,66397
6	-1,58814
7	0,477979
8	0,563826
9	0,811351
10	-1,27473
11	-0,17875
12	0,950451
13	1,273808
14	0,504963
15	4,937354
16	6,805955
17	7,841842
18	7,680164
19	7,604332
20	6,798973
21	7,260945
22	5,768009
23	-0,27723
24	-1,41899
25	-0,24464
26	-0,17882
27	-0,3405
28	-0,01714
29	-1,65396
30	1,778874
31	0,864604
32	0,627094
33	2,854822
34	3,102348
35	-0,60059
36	-1,66337
37	-1,55749
38	0,474287
39	1,561954
40	0,80766

---

---

Смотрите также файлы

• Приложение а (Обязательное) План цеха 2.docx

• Основы цитологии.doc

• Гапоу ио итам.docx

• Задача 6.doc

• Практическая часть Упражнение Мои жизненные сферы. Приоритеты.docx