Файл: Министерство науки и высшего образования рф федеральное государственное бюджетное учреждение высшего образования Российский государственный геологоразведочный университет имени Серго Орджоникидзе мгри.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 58
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа №8 «Преобразование данных по методу главных компонент
В основе метода лежит анализ структуры ковариационной матрицы. Главные компоненты – это собственные векторы ковариационной матрицы. Пусть имеются данные измерений двух признаков X1 и X2:
| X1 | X2 |
| 10,373 | 6,76 |
| 4,373 | 9,373 |
| 13,373 | 7,373 |
| 15,373 | -13,627 |
| 14,373 | -10,627 |
| 13,373 | -12,627 |
| 6,76 | -7,627 |
| 6,76 | -6,627 |
| 5,76 | -6,627 |
| 11,76 | -13,627 |
| 9,76 | -6,627 |
| 7,76 | 0,76 |
| 5,76 | -1,24 |
| 11,28 | 5,72 |
| -6,28 | 6,72 |
| -8,28 | 22,72 |
| -16,28 | 11,72 |
| -15,28 | 12,72 |
| -14,28 | 14,72 |
| -11,72 | 12,72 |
| -14,28 | 10,72 |
| -9,4 | 7,4 |
| 12,373 | -0,24 |
| 18,373 | 3,76 |
| 10,373 | -5,627 |
| 8,373 | -10,627 |
| 9,373 | -9,627 |
| 7,373 | -11,627 |
| 15,373 | -7,627 |
| 4,76 | 1,76 |
| 7,76 | -0,24 |
| 9,76 | 2,76 |
| 0,76 | 2,76 |
| -0,24 | 2,76 |
| 14,373 | 1,76 |
| 14,373 | -10,62 |
| 13,373 | -12,27 |
| 6,76 | -7,67 |
| 2,73 | -6,62 |
| 5,76 | -6,67 |
Вычислим
:
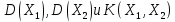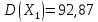
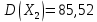
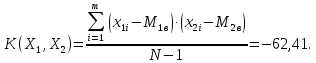
Ковариационная матрица для полученных данных имеет вид:
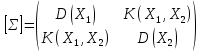
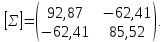
Напишем характеристическую матрицу:
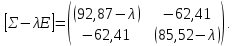
Вычислим определитель матрицы. Получим характеристический многочлен:
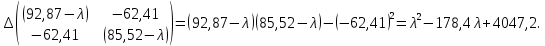
Приравняем характеристический многочлен к нулю и определим его корни:
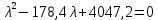
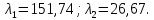
Вычислим собственные вектора.
Подстановка первого собственного значения дает:
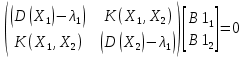
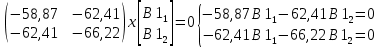
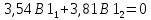
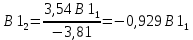
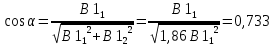
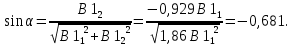
Нормированные значения компонент собственного вектора определяют
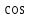и 
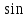угла наклона большой полуоси.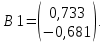
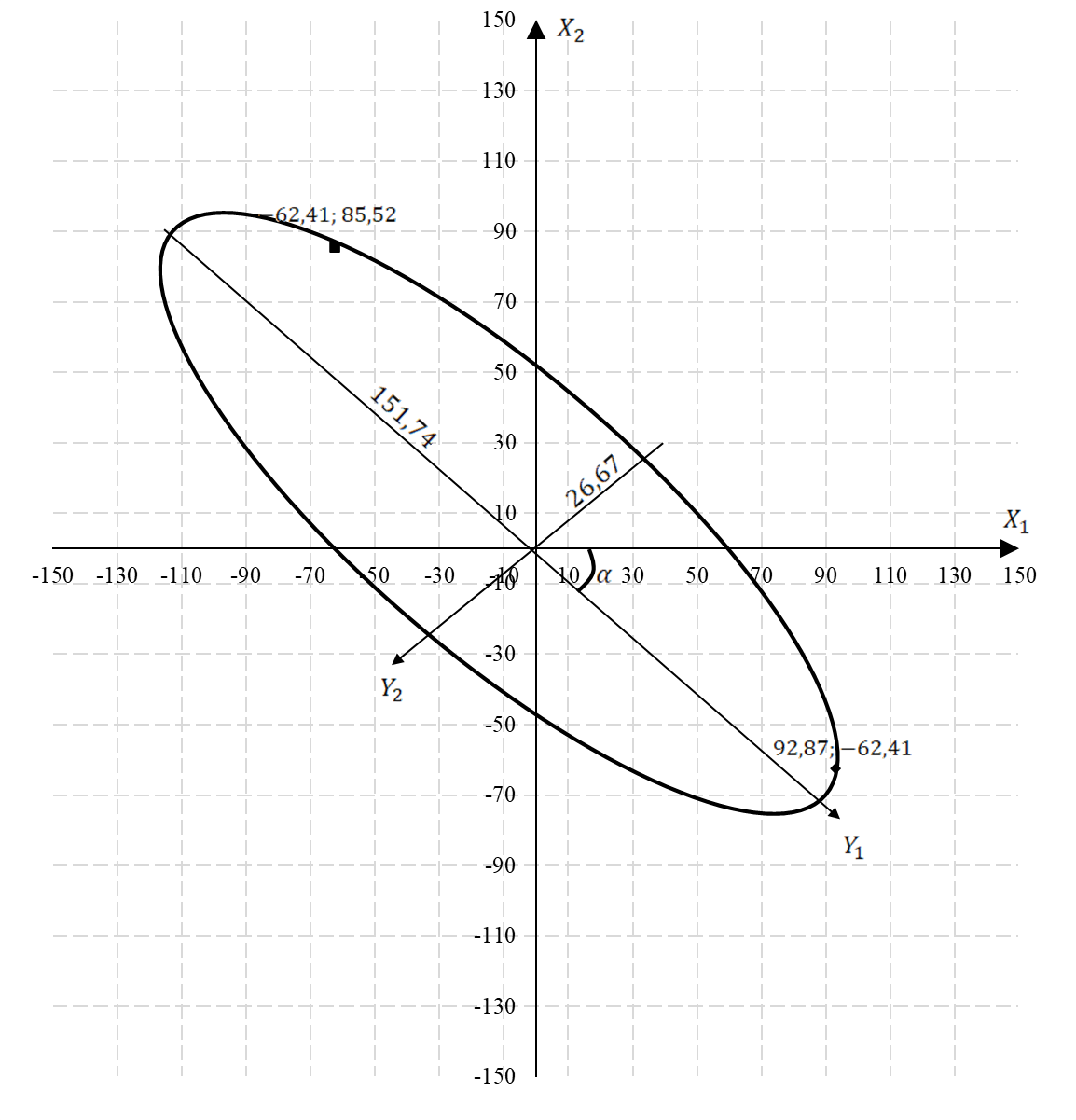
Отношение компонент первого собственного вектора равно тангенсу угла наклона большой полуоси эллипса
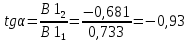
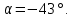
Подстановка второго собственного значения дает:
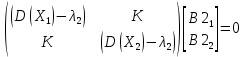
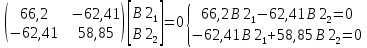
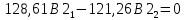
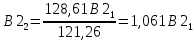
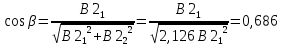
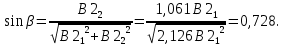
Нормированные значения компонент собственного вектора определяют
и 
угла наклона малой полуоси.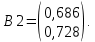
Отношение компонент второго собственного вектора определяет тангенс угла наклона малой полуоси эллипса:
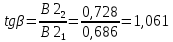
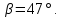
Сумма собственных значений равна следу матрицы:
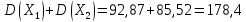
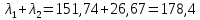
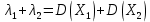
Таким образом, вклад переменной
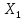в общую дисперсию: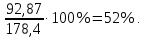
Вклад переменной
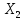в общую дисперсию: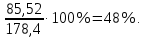
Главные оси эллипса также характеризуют суммарную дисперсию, следовательно:
Первая главная ось оставляет:
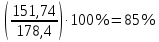
суммарной дисперсии, а вторая главная ось эллипса:
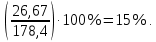
Таким образом, главная ось эллипса учитывает большую часть изменчивости множества данных.
Угол поворота новых осей координат по отношению к старой определяется из координат собственных векторов:
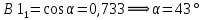
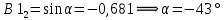
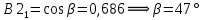
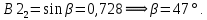
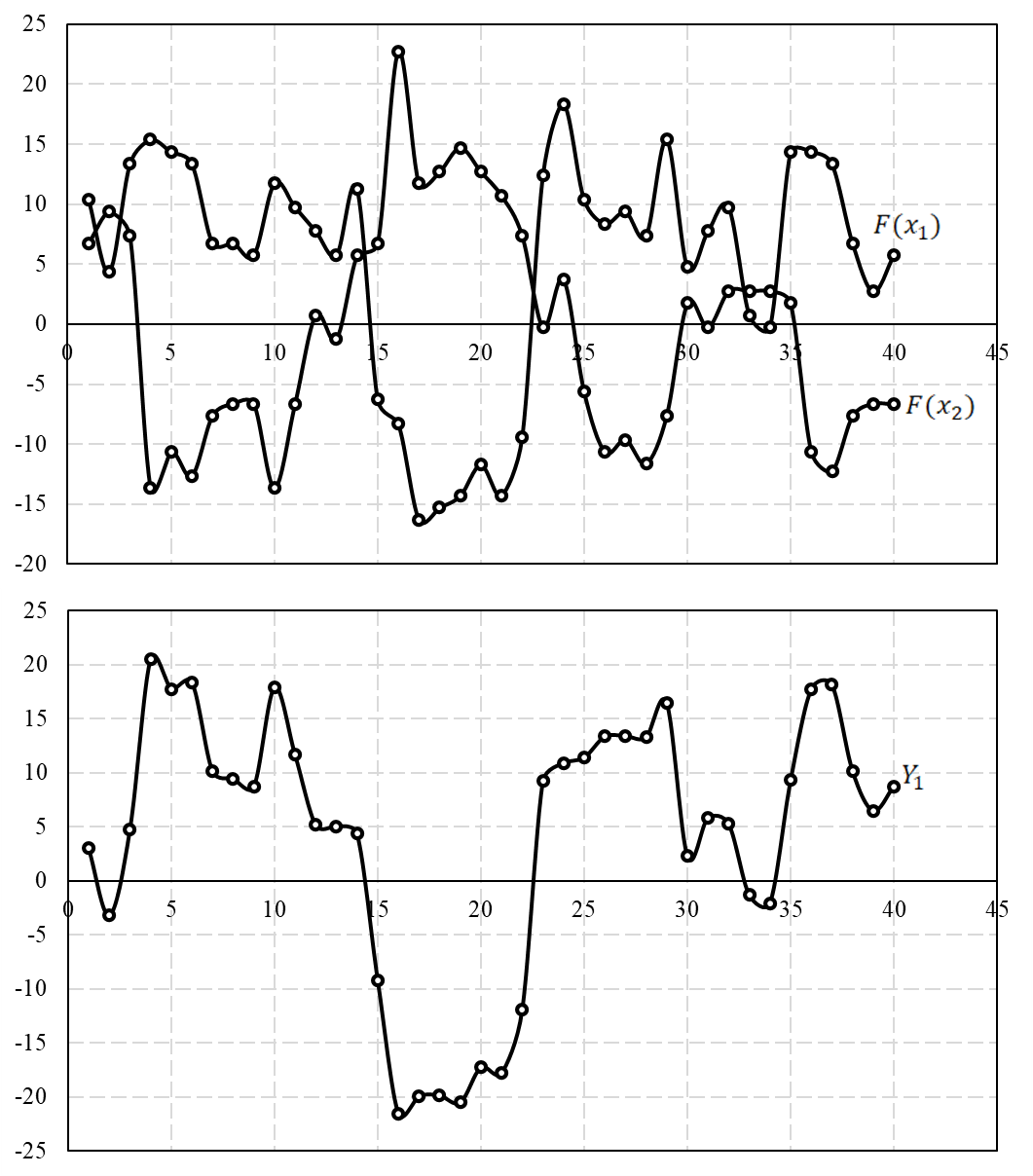
Если сделаем преобразование вида:
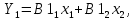
где
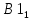и 
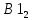– координаты первого собственного вектора.то получим новое множество данных. Новая переменная, соответствующая первому собственному вектору, называется первой главной компонентой.
Аналогичное преобразование:
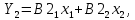
где
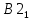и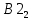 
– координаты второго собственного вектора, приводит к преобразованию прежних координат в переменную. Эта переменная является второй главной компонентой.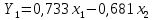
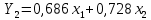
| № | Y1 | Y2 | № | Y1 | Y2 |
| 1 | 3,000 | 12,037 | 21 | -17,768 | -1,992 |
| 2 | -3,178 | 9,823 | 22 | -11,930 | -1,061 |
| 3 | 4,781 | 14,541 | 23 | 9,233 | 8,313 |
| 4 | 20,548 | 0,625 | 24 | 10,907 | 15,341 |
| 5 | 17,772 | 2,123 | 25 | 11,435 | 3,019 |
| 6 | 18,401 | -0,019 | 26 | 13,374 | -1,993 |
| 7 | 10,149 | -0,915 | 27 | 13,426 | -0,579 |
| 8 | 9,468 | -0,187 | 28 | 13,322 | -3,407 |
| 9 | 8,735 | -0,873 | 29 | 16,462 | 4,993 |
| 10 | 17,900 | -1,853 | 30 | 2,291 | 4,547 |
| 11 | 11,667 | 1,871 | 31 | 5,852 | 5,149 |
| 12 | 5,171 | 5,877 | 32 | 5,275 | 8,705 |
| 13 | 5,067 | 3,049 | 33 | -1,322 | 2,531 |
| 14 | 4,373 | 11,902 | 34 | -2,055 | 1,845 |
| 15 | -9,180 | 0,584 | 35 | 9,337 | 11,141 |
| 16 | -21,542 | 10,860 | 36 | 17,768 | 2,129 |
| 17 | -19,915 | -2,636 | 37 | 18,158 | 0,241 |
| 18 | -19,863 | -1,222 | 38 | 10,178 | -0,946 |
| 19 | -20,492 | 0,920 | 39 | 6,509 | -2,947 |
| 20 | -17,253 | 1,220 | 40 | 8,764 | -0,904 |
