Файл: Министерство науки и высшего образования рф федеральное государственное бюджетное учреждение высшего образования Российский государственный геологоразведочный университет имени Серго Орджоникидзе мгри.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 29.11.2023

Просмотров: 54

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ

Федеральное государственное бюджетное учреждение высшего образования «Российский государственный геологоразведочный университет имени Серго Орджоникидзе»

МГРИ

Факультет технологии разведки и разработки

Кафедра горного дела

ЛАБОРАТОРНЫЕ РАБОТЫ № 1-8

Часть I. Создание математической модели документации горных пород

Часть II. Создание математической модели эталонных объектов

по учебной дисциплине: «Математическое моделирование»
Вариант 7

Выполнил: студент группы РТБ-18 Закиров Р. Р.

Проверил: профессор Сикорский В. А.

Москва 2022

Часть I. Создание математической модели документации горных пород

Лабораторная работа №1 «Выборочный метод»

    1. Построение эмпирической интегральной и дифференциальной функции распределения

Дана выборка (объемом N =54) образцов горных пород, в каждом из которых определено содержание 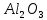в процентах.

Результаты измерений для каждого класса приведены в таблицах А, Б и В.

Класс А

Таблица А

11,28
10,69
11,18
8,2
10,6
9,73
8,71
9,96
8,21

12,02
8,27
7,17
7,88
7,27
8,66
8,59
6,82
6,46

7,82
10,81
9,82
10,7
10,25
7,73
12,23
11,04
9,12

9,4
12,53
7,26
8,77
5,98
10,39
8,77
8,97
6,84

7,17
8,07
3,99
10,25
8,39
11,56
9,69
5,6
12,41

8,97
10,33
8,26
6,23
10,57
11,81
9,73
5,25
10,85




  1. Интервал группирования:



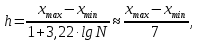
где 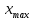– максимальное значение признака в выборке;

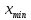– минимальное значение признака в выборке;

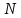– объем выборки.

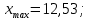
В нашем случае: 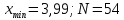, тогда: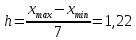



Поскольку число интервалов выбирается произвольно, ориентируясь на полученное значение, примем в качестве интервала группирования величину близкую, но более удобную.

Таким образом, .

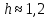  1. Разобьем весь интервал изменения измеренного признака на частичные интервалы длиной .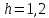

Для этого левая граница первого частичного интервала выбирается меньше минимального числа. В нашем случае 3.

То есть интервалы группирования примут следующие значения:

(3…4,2)(4,2…5,4)(5,4…6,6)…(11,4…12,6)

Найдём середины интервалов по формуле:



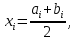
где 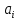– левая граница соответствующего интервала группирования;

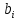– правая граница соответствующего интервала группирования.

Интервалы группирования:

















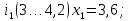
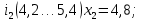
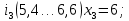
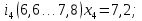
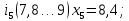
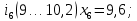
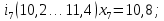
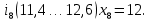
  1. Вычислим частоту попадания измеряемой величины в каждый интервал .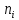

От 3 до 4,2 ( 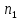); таких 1;

От 4,2 до 5,4 ( 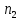); таких 1;

От 5,4 до 6,6 ( 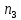); таких 4;

От 6,6 до 7,8 ( 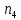); таких 7;

От 7,8 до 9 ( 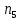); таких 15;

От 9 до 10,2 ( 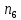); таких 7;

От 10,2 до 11,4 ( 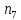); таких 13;

От 11,4 до 12,6 ( 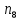); таких 6.

Сумма всех частот должна быть равна объему выборки, согласно формуле:



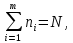
где m– количество интервалов группирования.

В нашем случае:

1+1+4+7+15+7+13+6=54

Вычислим относительные частоты, плотность относительных частот и накопление относительной частоты по следующим формулам:



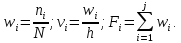
Результаты занесём в таблицу:

Интервал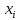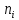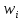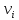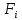










3
4,2
3,6
1
0,02
0,02
0,02

4,2
5,4
4,8
1
0,02
0,02
0,04

5,4
6,6
6
4
0,07
0,06
0,11

6,6
7,8
7,2
7
0,13
0,11
0,24

7,8
9
8,4
15
0,28
0,23
0,52

9
10,2
9,6
7
0,13
0,11
0,65

10,2
11,4
10,8
13
0,24
0,20
0,89

11,4
12,6
12
6
0,11
0,09
1,00



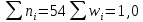
  1. На основании полученных результатов строим гистограммы:

Эмпирическая интегральная функция распределения





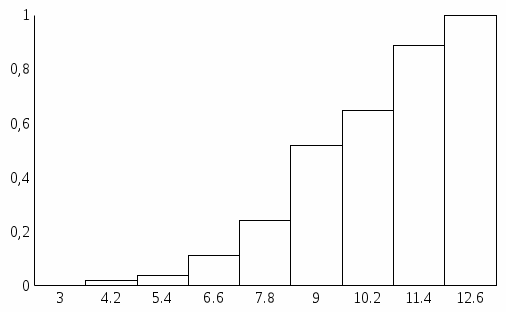
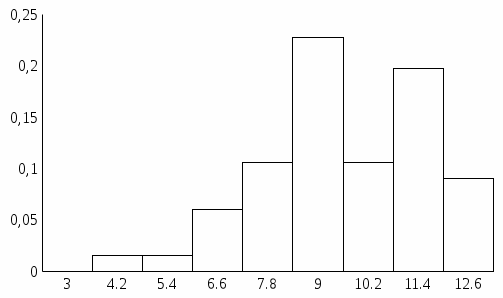
Эмпирическая дифференциальная функция распределения

Класс Б

Таблица Б

12,3
14,06
12,38
11,96
10,78
12,8
8,82
9,24
13,07

12,39
10,23
12,57
10,43
11,95
11,03
10,23
8,23
14,46

11,28
13,21
10,72
10,87
12,04
12,2
8,32
11,04
11,94

11,53
12,34
10,23
11,76
10,02
11,21
16,45
9,64
6,33

12,64
10,3
11,52
8,8
6,62
12,25
11,77
12,41
8,65

8,19
9,73
13,37
8,49
14,35
8,31
10,69
9,44
11,42



  1. Интервал группирования:



где
– максимальное значение признака в выборке;

– минимальное значение признака в выборке;

– объем выборки.

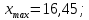
В нашем случае: 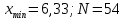, тогда: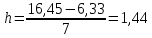



Поскольку число интервалов выбирается произвольно, ориентируясь на полученное значение, примем в качестве интервала группирования величину близкую, но более удобную.

Таким образом, .

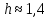  1. Разобьем весь интервал изменения измеренного признака на частичные интервалы длиной .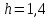

Для этого левая граница первого частичного интервала выбирается меньше минимального числа. В нашем случае 6.

То есть интервалы группирования примут следующие значения:

(6…7,4)(7,4…8,8)(8,8…10,2)…(15,8…17,2)

Найдём середины интервалов по формуле:



где – левая граница соответствующего интервала группирования;

– правая граница соответствующего интервала группирования.

Интервалы группирования:


















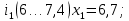
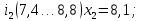
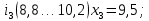
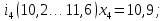
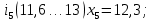
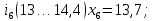
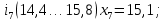
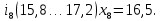
  1. Вычислим частоту попадания измеряемой величины в каждый интервал .

От 6 до 7,4 ( ); таких 2;

От 7,4 до 8,8 (

Смотрите также файлы