Федеральное агентство железнодорожного транспорта

Федеральное государственное бюджетное

образовательное учреждение высшего образования

«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА I»

(ФГБОУ ВО ПГУПС)

Кафедра «Физика»


ОБРАБОТКА РЕЗУЛЬТАТОВ ЛАБОРАТОРНОГО

ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА

Методические указания

к лабораторной работе № 100

Санкт-Петербург

2016

УДК 530.1

ББК 22.3

О-23

О
О-23
бработка результатов лабораторного физического эксперимента : метод. указания к лабораторной работе № 100 / Сост. Е. С. Громова, Е. Н. Бодунов. – СПб. : ФГБОУ ВО ПГУПС, 2016. – 33 с.

В методических указаниях рассмотрены методы обработки результатов физических лабораторных измерений, способы вычисления погрешностей при многократных и однократных измерениях, правила графического представления экспериментальных данных. Приведены примеры вывода формул погрешностей при косвенных измерениях. Дано подробное описание лабораторной работы, направленной на ознакомление с нормальным законом распределения и на освоение студентами алгоритма обработки результатов прямых многократных измерений.

Методические указания предназначены для студентов технических вузов, выполняющих лабораторные работы по курсу общей физики.
УДК 530.1

ББК 22.3


© ФГБОУ ВО ПГУПС, 2016


Введение

Основная задача всякого физического эксперимента, в том числе лабораторного, состоит в измерении физических величин. Измерить какую-либо физическую величину – значит сравнить ее с другой однородной физической величиной, условно принятой за единицу измерения. В результате каждого отдельного измерения (оно называется наблюдением) получают числовое значение измеряемой величины.

Измерения не могут быть абсолютно точными. Никакие измерения не дают возможности получить истинное значение измеряемой величины, что объясняется как принципиально ограниченной точностью приборов, так и природой самих объектов измерения. Всегда имеется некоторая неопределенность в значении измеряемой величины. Эта неопределенность характеризуется погрешностью – отклонением измеренного значения величины от ее истинного значения.

Многократно измеряя любую физическую величину, можно, вообще говоря, получить какие угодно результаты. Например, измеряя длину некоторого тела, получили значения: 171, 172, 169, 173, 170, 169, 171 см, а также 170 мм и 169 дм. Результаты двух последних измерений могут быть и ошибочными, являясь, например, следствием небрежного ведения записей. Однако их наличие подчеркивает то обстоятельство, что принципиально и результат измерений, и его погрешность могут быть любыми, следовательно, оценивать точность измерения указанием результата и его погрешности неверно – они могут принимать любые значения.

Вместе с тем из анализа вышеприведенного ряда результатов видно, что большие по величине погрешности (соответствующие, по-видимому, двум последним результатам) маловероятны. Отсюда следует, что для правильной характеристики точности результата необходимо указывать не только величину погрешности, но и соответствующее ей значение вероятности.

Таким образом, при выполнении измерений и обработке их результатов каждый экспериментатор должен иметь в виду следующие обстоятельства:

1) всякое измерение должно по возможности быть проверено путем многократного повторения;

2) при измерении может быть получен лишь приближенный результат;

3) степень приближенности результата должна быть задана величиной погрешности;

4) степень доверия к найденным границам погрешности выражается значением ее вероятности.
АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

Абсолютная погрешность i-го наблюдения какой-либо физической величины определяется разностью

(1)

где – значение физической величины, найденное в i-м наблюдении; x – истинное значение измеряемой величины, которое принципиально получить невозможно.

На практике вместо истинного значения величины x используют его наилучшее приближение.

Абсолютная погрешность выражается в тех же единицах, что и сама измеряемая величина. Значения абсолютной погрешности могут быть как положительными, так и отрицательными.

Для характеристики точности измерений недостаточно оперировать только значением абсолютной погрешности. Важно знать, какую долю составляет эта погрешность от значения измеряемой величины. Отношение

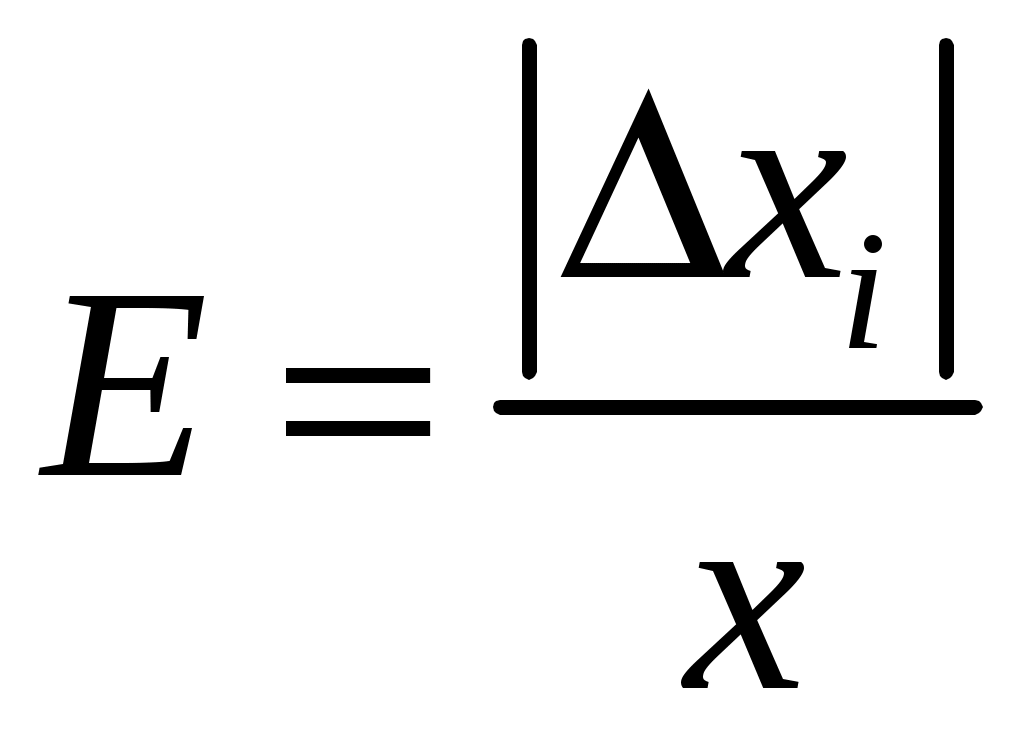(2)

называется относительной погрешностью i-го наблюдения какой-либо физической величины и выражается в долях или процентах. Относительная погрешность характеризует качество измерений.

Заметим, что выражения (1) и (2) определяют истинные значения абсолютной и относительной ошибок, которые не могут быть определены так же, как истинное значение самой измеряемой величины.

ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ И ДОВЕРИТЕЛЬНАЯ ПОГРЕШНОСТЬ

При обработке результатов измерений любой физической величины возникают две задачи. Первая состоит в нахождении по набору данных наилучшей оценки измеряемой величины , которую с наибольшим основанием можно принять за приближенное значение величины x. Вторая – в определении точности полученного результата.

Результат измерения физической величины представляют в виде



Приведенная запись означает, что существует определенная степень уверенности в том, что значение измеряемой величины находится в пределах рассчитанного по результатам наблюдений интервала , называемого доверительным. Величина называется доверительной погрешностью.

Указание значения доверительной вероятности P означает, что при проведении большого числа наблюдений в случаев результаты наблюдений измеряемой физической величины, выполненных с одинаковой тщательностью и одними и теми же измерительными приборами, попадут внутрь доверительного интервала.

Значения доверительной погрешности и доверительной вероятности однозначно связаны друг с другом, а именно: чем большим выбирается значение доверительной вероятности, тем больший доверительный интервал ей соответствует, и наоборот.

ВИДЫ ПОГРЕШНОСТЕЙ

По характеру, происхождению, а также по способам оценки и исключения влияния на результат измерений погрешности делят на три основные группы: случайные, систематические и грубые (промахи).

Систематической называется погрешность, остающаяся постоянной или закономерно изменяющаяся во времени при повторных измерениях одной и той же величины. Систематические погрешности связаны с ограниченной точностью прибора и метода измерений, а также с округлением при считывании значения со шкалы. Когда причины, вызывающие эти погрешности, известны, их можно исключить, уточняя метод измерения и вводя поправки к показаниям приборов.

Грубые погрешности (промахи) обычно связаны с отсутствием достаточной квалификации экспериментатора, неправильным отсчетом по прибору, неправильной записью результата наблюдения, невнимательностью и т. п. Обычно грубые погрешности хорошо заметны, так как при многократно проделанных измерениях соответствующие промахам результаты резко отличаются от остальных. Такие погрешности могут возникать в результате неустойчивой работы установки или отдельного прибора. Они могут быть устранены путем повторных измерений или снятием показаний другим экспериментатором.

Случайные погрешности обусловливаются большим количеством трудно учитываемых факторов, влияющих как на измерительные устройства, исследуемый физический объект или процесс, так и на самого экспериментатора. Такими факторами могут быть, например, колебания температуры элементов установки, напряженностей электрического и магнитного полей, движение воздуха, вибрация зданий и приборов, трение в движущихся элементах, погрешности при отсчете делений шкалы и т. п. Исключить случайные погрешности отдельных измерений невозможно, но величину таких погрешностей можно оценить, проводя повторные (многократные) измерения. Величина случайных погрешностей оценивается с помощью аппарата математической статистики и теории вероятностей.

ПРЯМЫЕ И КОСВЕННЫЕ ИЗМЕРЕНИЯ

По способу получения результата измерения делятся на прямые и косвенные. Если значение физической величины находят непосредственным отсчетом по шкале прибора, то такие измерения называются прямыми (измерения давления барометром, температуры – термометром, времени – секундомером, длины – штангенциркулем или линейкой, силы тока – амперметром и т. п.). Эти измерения могут быть однократными и многократными. Многократное измерение – повторение экспериментельной операции, в результате которой получается одно из значений измеряемой величины , называемых результатами наблюдений. Совокупность результатов наблюдений подлежит совместной обработке для получения результата измерения.

Часто прямое измерение физической величины оказывается невозможным или слишком трудоемким. При косвенных измерениях результат определяется по формулам на основе результатов прямых измерений других величин (например, определение электрического cопротивления образца по измеренным силе тока и напряжению). Одну и ту же величину часто можно найти путем как прямых, так и косвенных измерений. Например, скорость автомобиля может быть определена по спидометру (прямое измерение) или найдена делением пройденного пути на время движения (косвенное измерение).

При косвенных измерениях погрешность искомой физической величины накапливается из погрешностей прямых измерений величин, входящих в расчетную формулу.

ПОГРЕШНОСТИ МНОГОКРАТНЫХ ПРЯМЫХ ИЗМЕРЕНИЙ

(случайные погрешности)

Пусть при измерении физической величины X получены n результатов наблюдений , причем все измерения выполнены одним и тем же методом и с одинаковой степенью тщательности. Этот ряд значений величины называется выборкой. Предположим, что на результат измерений оказывают действие только случайные (неконтролируемые) факторы, а промахи и систематические ошибки отсутствуют.

Задача экспериментатора состоит в том, чтобы найти наилучшую оценку и доверительную погрешность результата измерений для заданного значения доверительной вероятности. Указанная задача строго решается с помощью теории вероятностей и математической статистики.

В большинстве случаев случайные ошибки подчиняются установленному Гауссом нормальному закону распределения, который выражается формулой

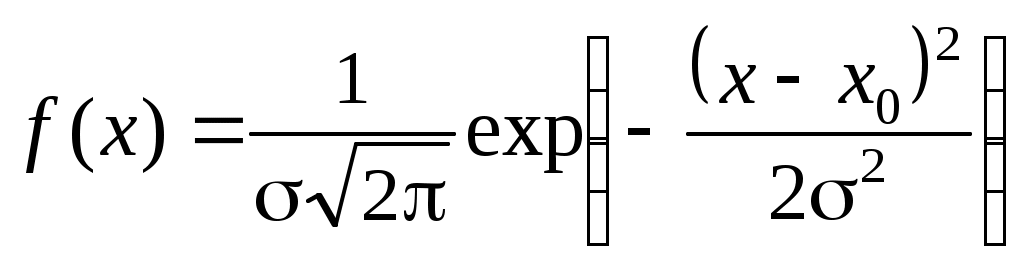, (3)

где x – числовое значение определяемой величины X; и – параметры распределения; – плотность вероятности (вероятность того, что значение принадлежит некоторому единичному интервалу значений), так что функция определяет вероятность попадания значения x в интервал от x до .

Параметр , соответствующий максимуму плотности вероятности , называется математическим ожиданием случайной величины X. Параметр называется среднеквадратичным отклонением величины X от ее математического ожидания и характеризует меру ее разброса относительно .

Очевидно, что



так как вероятность того, что случайная величина X вообще имеет какое-то значение, равна единице.

Поскольку максимальное значение плотность вероятности принимает при , то величину часто считают приблизительно равной истинному значению измеряемой величины. На рис. 1 представлен график этой функции.

Из теории вероятностей следует, что наилучшей оценкой истинного значения измеряемой случайной величины X является среднее арифметическое (выборочное среднее) значение

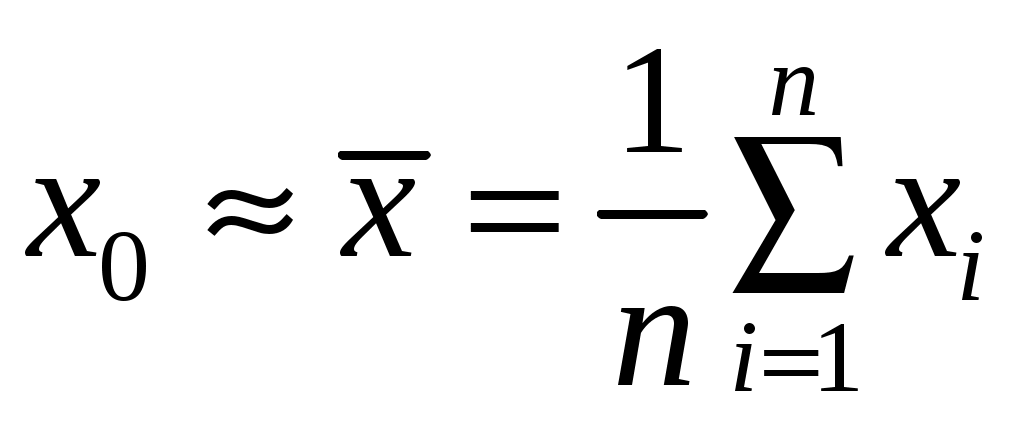. (4)

Заметим также, что с увеличением значения увеличивается разброс отсчетов, т. е. точность измерений понижается. В условиях реального эксперимента точное значение неизвестно. По многократным измерениям можно получить приближенную оценку этого параметра в виде среднеквадратичной погрешности отдельного результата наблюдения

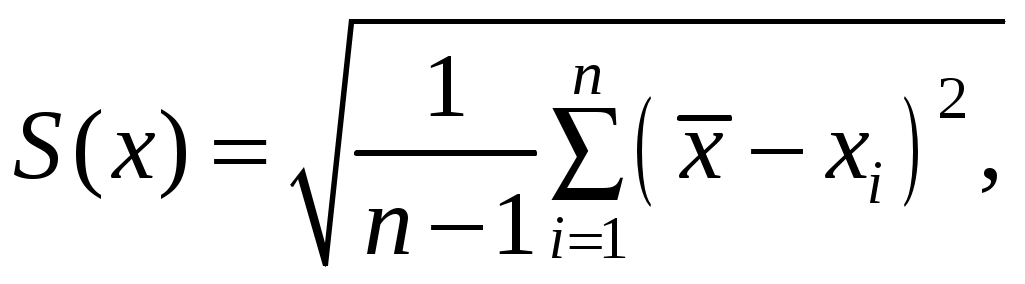(5)

которая учитывает ошибку каждого отдельного измерения и при неограниченном увеличении числа наблюдений ( ) стремится к истинной среднеквадратичной ошибке .


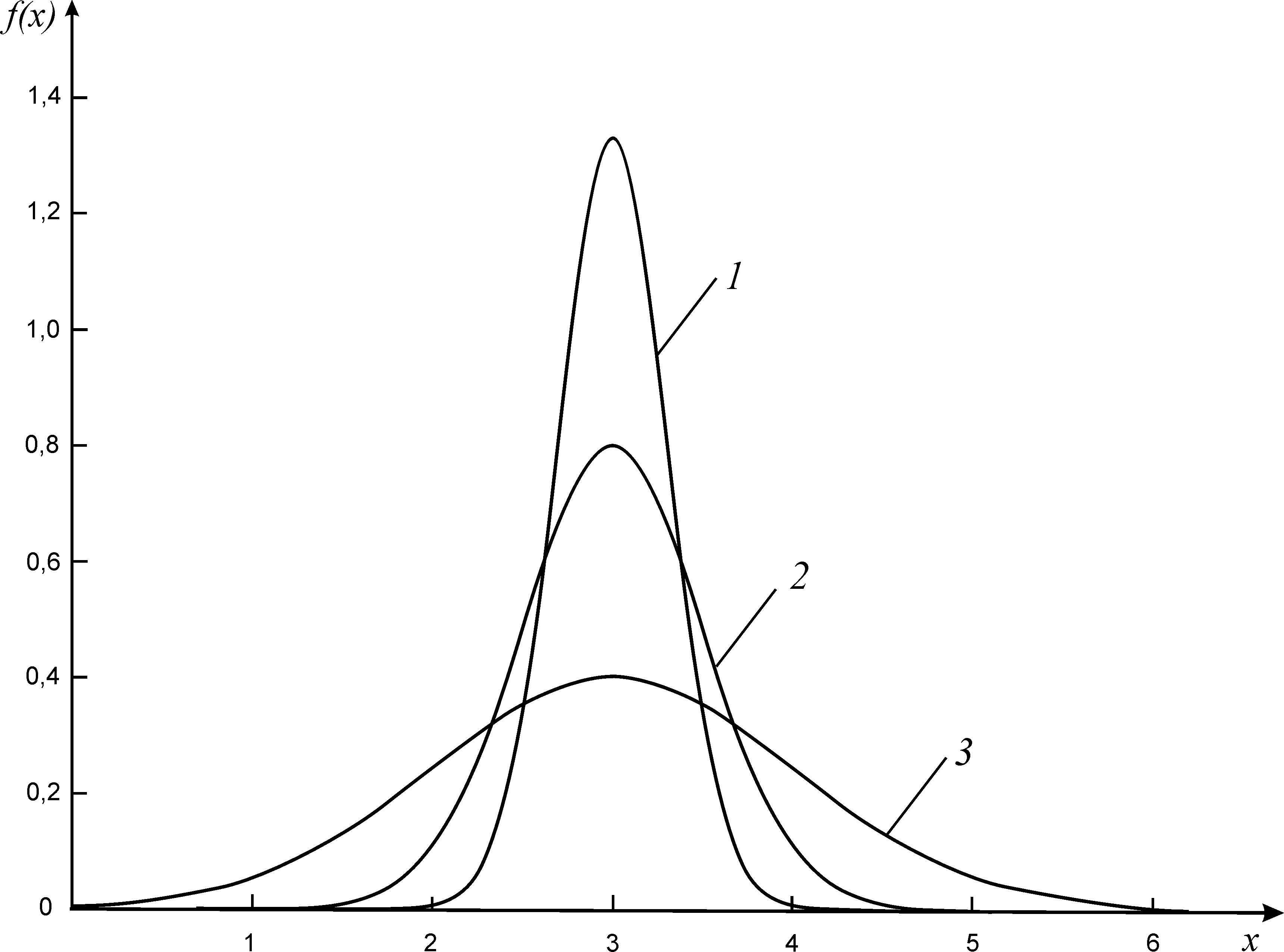
Рис. 1. Нормальное (гауссово) распределение

(1 –   /4, 2 –   /2, 3 –   )

Если провести несколько серий многократных измерений, т. е. получить несколько выборок и для каждой вычислить выборочное среднее, то получим выборку для новой случайной величины , которая также распределена нормально с математическим ожиданием . Однако параметр меньше, чем :

.

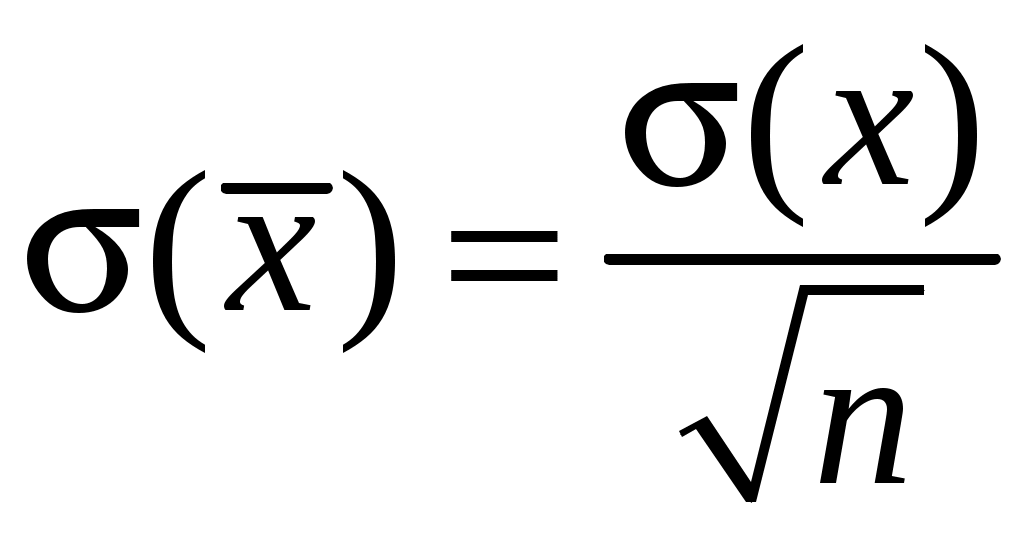Это означает, что выборочное среднее имеет приблизительно в меньший разброс, чем единичное измерение x. Поэтому для оценки лучше использовать выборочное среднее и среднеквадратичную погрешность среднего арифметического результата измерения, которая вычисляется по формуле

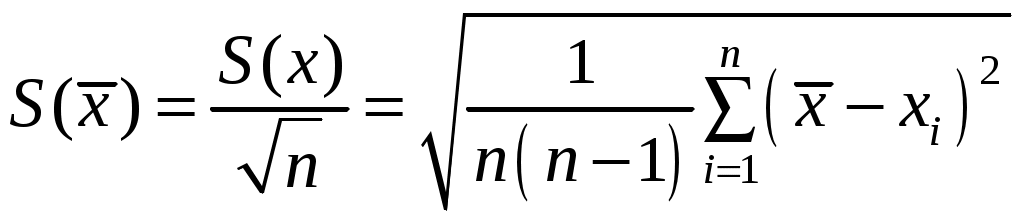. (6)

В выражениях (5) и (6) обозначение среднеквадратичной ошибки заменено на обозначение S, чтобы подчеркнуть, что величины и вычисляются на основе ограниченного числа наблюдений, т. е. являются эмпирическими оценками теоретических параметров и , т. е. , .

При проведении реальных технических измерений число наблюдений, как правило, невелико – в пределах от 2 до 20. В такой ситуации рассмотренный метод приводит к существенному искажению результатов. В теории погрешностей при малом числе измерений применяют специальный метод вычисления доверительного интервала, основанный на распределении Стьюдента. В 1908 г. английский математик Уильям Госсет (псевдоним Стьюдент) доказал, что указанными соотношениями можно пользоваться и при небольшом числе наблюдений ( ), если на конечной стадии ввести в расчет специальный коэффициент, величина которого зависит от числа наблюдений n и требуемого значения доверительной вероятности P, – так называемый коэффициент Стьюдента (табл. 1).
Таблица 1

Коэффициенты Стьюдента t_n,P

n	P
	0,68	0,80	0,90	0,95	0,98	0,99
2	2,0	3,1	6,3	12,7	31,8	63,7
3	1,3	1,9	2,9	4,3	7,0	9,9
4	1,3	1,6	2,4	3,2	4,5	5,8
5	1,2	1,5	2,1	2,8	3,7	4,6
6	1,2	1,5	2,0	2,6	3.4	4,3
7	1,1	1,4	1,9	2,4	3,1	4,0
8	1,1	1,4	1,9	2,4	3,0	3,7
9	1,1	1,4	1,9	2,3	2,9	3,4
10	1,1	1,4	1,83	2,26	2,8	3,35
60	1,0	1,3	1,7	2,0	2,4	2,7
∞	1,0	1,3	1,64	1,96	2.3	2,58

Рекомендуется следующий алгоритм проведения и обработки результатов прямых многократных измерений:

1. Прямыми измерениями получить ряд значений измеряемой величины.

2. Вычислить среднее арифметическое значение результата измерений:

.

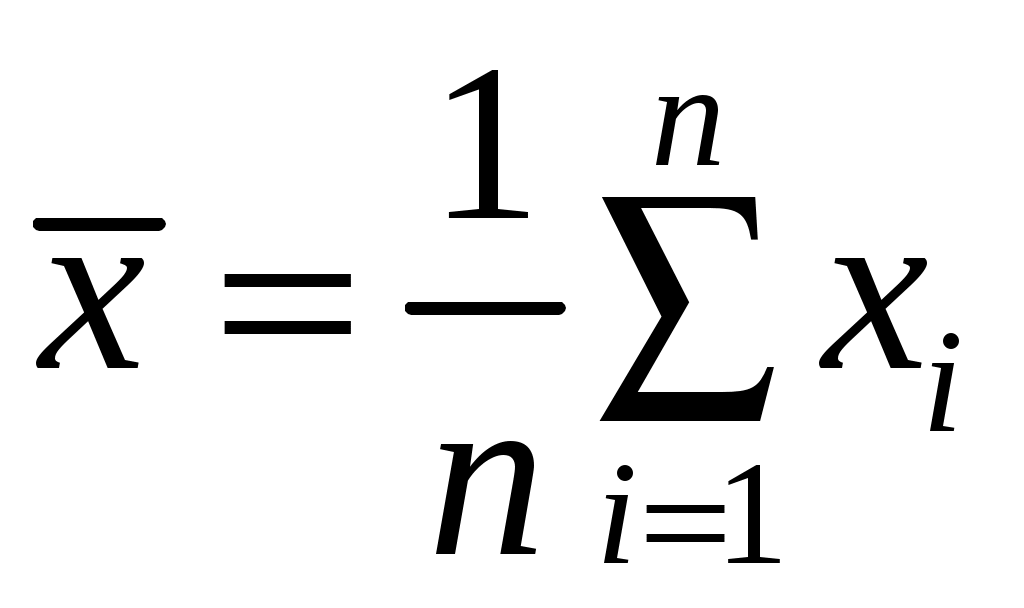3. Вычислить отклонения отдельных результатов наблюдений от среднего:



4. Вычислить значения и сумму .

5. Для данного значения числа измерений n и выбранной доверительной вероятности P найти по таблице коэффициент Стьюдента и вычислить случайную погрешность:

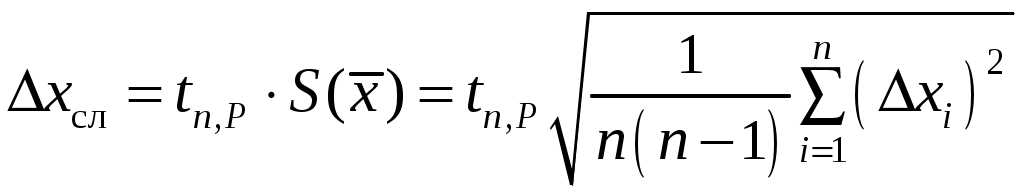. (7)

6. Округлив погрешность и предварительный результат, записать окончательный результат измерений в виде



Пример А. Обработка результатов прямых многократных измерений диаметра Д некоторого вала штангенциркулем.

Получены 6 значений , которые внесены во 2-й столбец табл. 2.

---

Таблица 2

Результат измерения диаметра вала

№ п/п	Дi, мм	ΔДi, мм	(ΔДi)2, мм
1	36,2	0,05	25·10–4
2	36,3	0,15	225·10–4
3	36,0	– 0,15	225·10–4
4	36,1	– 0,05	25·10–4
5	36,2	0,05	25·10–4
6	36,1	– 0,05	25·10–4

Под 2-м столбцом таблицы приведено среднее значение диаметра вала (предварительный результат), а под 4-м столбцом – значение суммы . Такое оформление результата измерений компактно и удобно для дальнейшей обработки.

Из данных табл. 2 вычисляем среднеквадратичную погрешность среднего арифметического результата измерения:



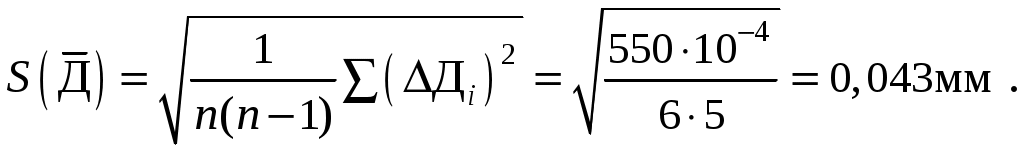
По данным табл. 1 определяем коэффициент Стьюдента . Тогда случайная погрешность



и окончательный результат

мм, .

ОКРУГЛЕНИЕ РЕЗУЛЬТАТОВ И ПОГРЕШНОСТЕЙ РЕЗУЛЬТАТОВ

---

ИЗМЕРЕНИЙ. ЗАПИСЬ ОКОНЧАТЕЛЬНОГО РЕЗУЛЬТАТА

Поскольку значения физических величин, полученные в результате измерений, имеют погрешности, они выражаются не точными, а приближенными числами. Незначащими цифрами приближенного числа называются нули, стоящие слева от первой отличной от нуля цифры в десятичных дробях, и нули, поставленные в конце числа вместо цифр, отброшенных при округлении. Остальные цифры называются значащими. Например, в числе 0,00123 значащими являются цифры 1, 2, 3; в числе 508 000, полученном округлением числа 507 893, последние три нуля – незначащие. В конце числа могут быть и значащие нули. В качестве примера можно привести выражение 5 км = 5000 м. Здесь нули не заменяют отброшенные при округлении цифры, а выражают точное соотношение между единицами длины.

Для того чтобы числа не содержали незначащих нулей слева, их принято записывать в так называемой рационализированной форме, которую можно символически представить в виде выражения

,

где – цифры, причем ; c – показатель степени.

При такой записи числа рассмотренных примеров имеют вид 0,00123 = = 1,23·10^–2; 508 000 = 5,08 · 10⁵. Значащие цифры при такой записи не отбрасываются: 5 км = 5,000 · 10³ м.

При промежуточных расчетах и окончательной записи следует соблюдать следующие правила.

1. Все предварительные расчеты результатов измерений следует производить не менее чем до трех и не более чем до четырех значащих цифр.

2. Значение доверительной погрешности достаточно предварительно рассчитать с точностью до двух значащих цифр, а для окончательной записи округлить до одной значащей цифры. Данное правило объясняется тем, что при небольшом числе наблюдений (как правило, в учебной лаборатории их не более 5–7) значение погрешности определяется весьма приближенно и нет особого смысла сохранять в записи большее число значащих цифр.

3. Разряды последних приводимых в окончательной записи

---

значащих цифр результата и его погрешности должны совпадать.

Таблица 3

Примеры применения правил округления

№ п/п	Значение измеренной величины	Доверительная погрешность	Правильная запись окончательного результата
1	H = 4,062 м	ΔH = 0,0239 м	H = (4,06 ± 0,02) м, P = 0,90
2	R = 3,92 · 106 Ом	ΔR = 0,18 · 106 Ом	R = (3,9 ± 0,2) · 10–6 Ом, P = 0,90
3	q = –3,21 · 10–19 Кл	Δq = 2,67 · 10–20 Кл	q = (–3,2 ± 0,3) · 10–19 Кл, P = 0,90
4	α = 1,07 · 10–4 K–1	Δα = 10–6 K–1	α = (1,07 ± 0,01) · 10–4 K–1, P = 0,90

ПОГРЕШНОСТИ ОДНОКРАТНЫХ ПРЯМЫХ ИЗМЕРЕНИЙ

(приборные погрешности)

Однократное измерение величины X дает единственный результат, который и принимается за результат измерения. Иногда однократность является вынужденной (если, например, измерения уникальны и дорогостоящи). Однократными измерениями ограничиваются и тогда, когда при повторных наблюдениях получаются одинаковые по значению результаты и их дальнейшее повторение лишено смысла. Однако это не означает, что единственное значение, полученное при измерении, является точным. Абсолютно точных приборов не существует, результаты любых измерений будут содержать ошибки, вносимые самими приборами. В большинстве случаев выбор между однократными и многократными измерениями делает экспериментатор, анализируя как качество средств измерения, так и особенности самой измеряемой величины.

Погрешность результата прямого однократного измерения зависит от того, каким прибором или инструментом оно выполняется. У многих приборов, в основном электроизмерительных, на лицевой панели указывается так называемый класс точности. Класс точности

---

K представляет собой отношение предельно допустимой (предельной) погрешности прибора к верхнему пределу измерения прибора, выраженное в процентах:

,

откуда можно вычислить предельно допустимую погрешность по формуле

. (8)

Пример Б. Верхний предел измерения вольтметра , класс точности . Тогда предельно допустимая погрешность данного прибора



Это значение погрешности неизменно при любом показании прибора. Доверительная вероятность погрешностей, определяемых по формуле (8), полагается равной единице .

На электрических сопротивлениях и емкостях предельные погрешности обычно указывают в процентах по отношению к их номиналу. Например, запись на сопротивлении



означает, что предельная погрешность данного сопротивления составляет .

Цифровые измерительные приборы имеют, как правило, предельную погрешность, равную единице последнего разряда при индикации результата.

В табл. 4 указаны предельные погрешности приборов и инструментов, наиболее часто используемых в лабораторном физическом практикуме.

Погрешности, указанные в табл. 4, включают в себя неточности изготовления приборов, погрешности в нанесении их шкал, а также погрешности счета показаний (округление отсчетов), которые поэтому отдельно не рассматриваются. Еще раз отметим, что погрешности, приведенные в этой таблице, являются предельными, т. е. отвечают вероятности

---

Смотрите также файлы

• Решение Момент инерции шара радиуса R, относительно оси, проходящей через его центр определяется по формуле (1).docx

• Развитие пенсионных систем в развитых странах мира и России. Абдуллина Алия.pptx

• Методические рекомендации по написанию практикума соответствуют рабочей программе дисциплины Административное право и Административнопроцессуальное право.pdf

• Каковы рекомендации врача.doc

• 1. зачетные соревнования на учебных занятиях.docx