Файл: Федеральное агентство железнодорожного транспорта Федеральное государственное бюджетное.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 64
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
результата измерений по общей формуле (13):

7. Округлив результат измерений и погрешность, записать окончательный результат в виде
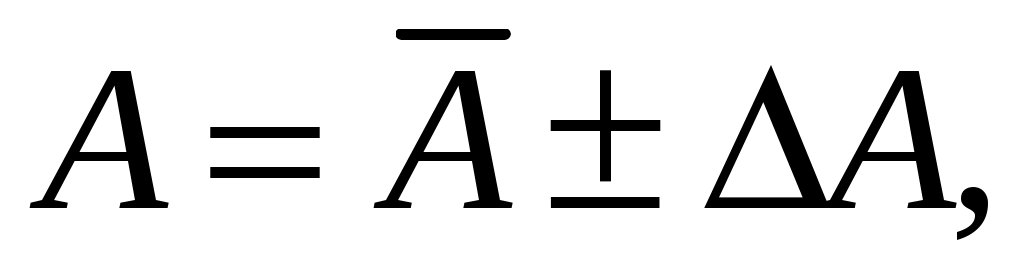

НЕВОСПРОИЗВОДИМЫЕ КОСВЕННЫЕ ИЗМЕРЕНИЯ
Иногда при выполнении косвенных измерений невозможно повторить наблюдения в тождественных условиях относительно одного или нескольких аргументов измеряемой функции. Например, при измерении коэффициента вязкости жидкости в нее бросают металлические шарики (дробинки). Каждый из брошенных в жидкость шариков сразу же достать нельзя. Условия опытов, повторенных с разными шариками, не будут одинаковыми из-за различия размеров и формы шариков, различного состояния их поверхностей и т. д. В этом случае говорят, что косвенные измерения невоспроизводимы. Тем не менее коэффициент вязкости характеризует одну и ту же исследуемую жидкость и расчет должен давать близкие значения этого коэффициента для всех шариков.
Рекомендуется следующий порядок обработки результатов невоспроизводимых косвенных измерений.
1. Определить значение искомой функции для каждого i-го невоспроизводимого наблюдения, исходя из найденных экспериментальных значений аргументов
для каждого i-го невоспроизводимого наблюдения, исходя из найденных экспериментальных значений аргументов  :
:
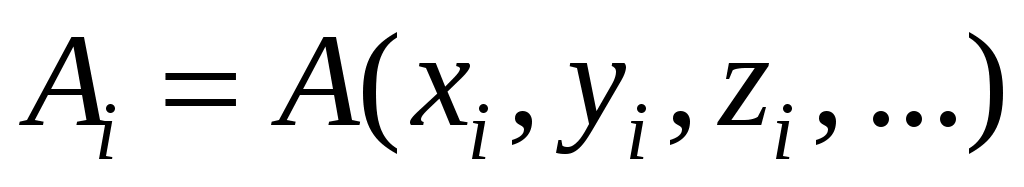 .
.
2. Каждое из определенных таким образом значений рассматривается затем как случайная величина с нормальным законом распределения погрешностей
рассматривается затем как случайная величина с нормальным законом распределения погрешностей 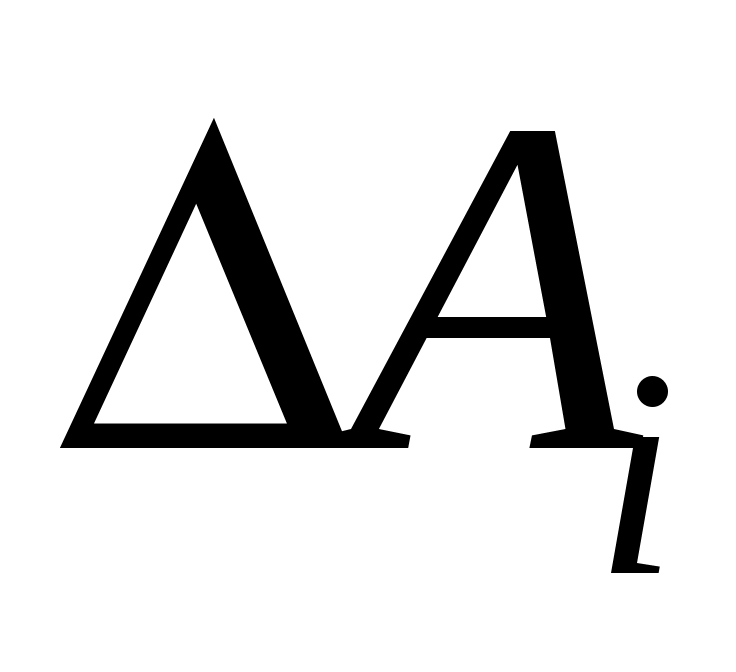 . Иначе говоря, значения
. Иначе говоря, значения  рассматриваются как результаты прямых многократных измерений физической величины A. В соответствии с этим в качестве наиболее вероятного значения берется среднее арифметическое
рассматриваются как результаты прямых многократных измерений физической величины A. В соответствии с этим в качестве наиболее вероятного значения берется среднее арифметическое
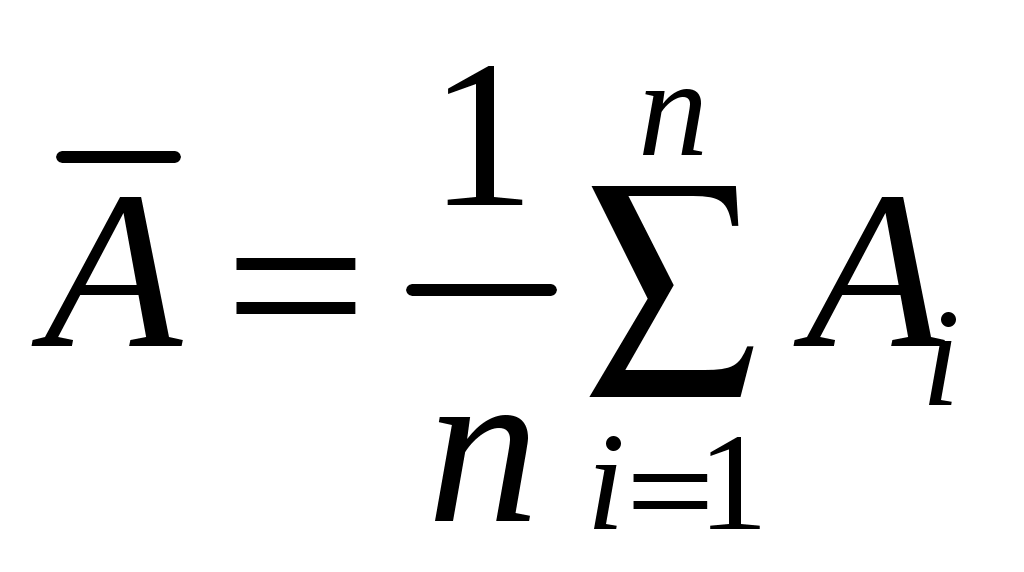 ,
,
а погрешность вычисляется как случайная по формуле
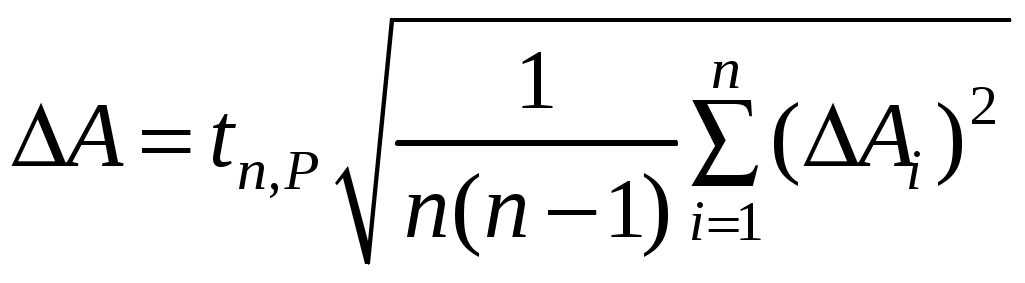 ,
,
т. е. как при обработке результатов прямых многократных измерений.
ПРИМЕРЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ
Пример 1. В работе № 103 коэффициент поверхностного натяжения жидкости определяется по расчетной формуле
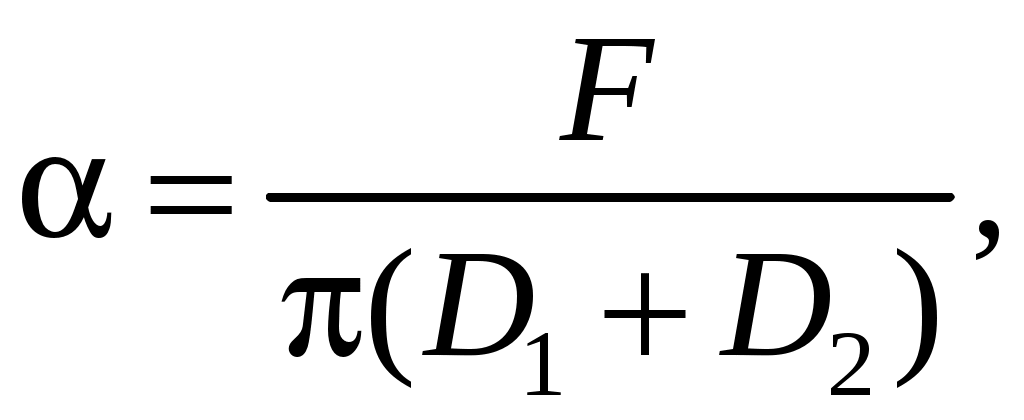 (16)
(16)
где F – сила поверхностного натяжения;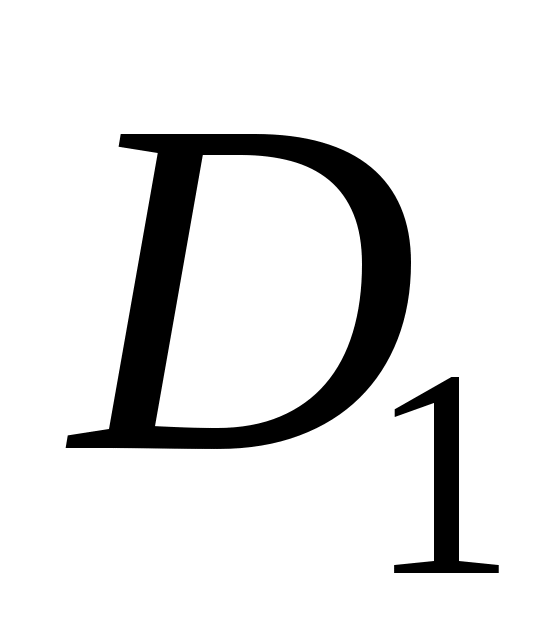 и
и 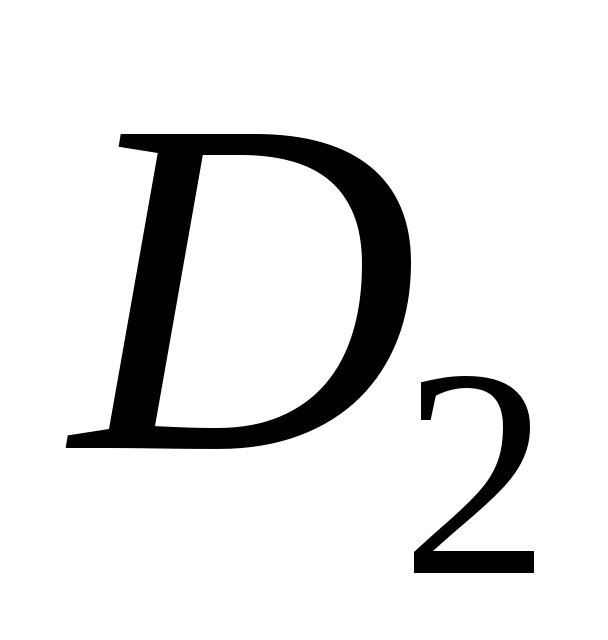 – соответственно внутренний и внешний диаметры кольца, погруженного в жидкость.
– соответственно внутренний и внешний диаметры кольца, погруженного в жидкость.
Для получения расчетной формулы погрешности учтем, что выражение (16) относительно удобно для логарифмирования (содержит три множителя: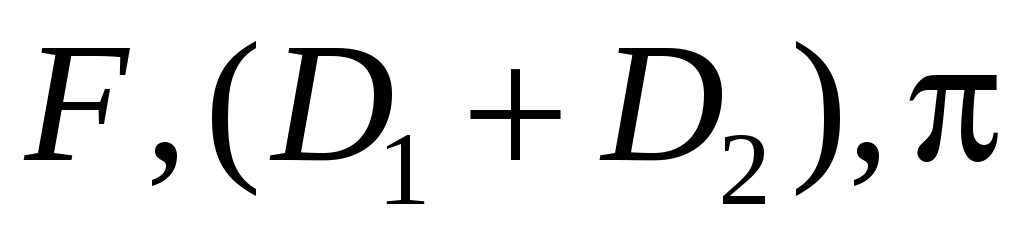 ) и, следовательно, целесообразно искать погрешность по формуле (15) с учетом замены соответствующих обозначений функции и аргументов:
) и, следовательно, целесообразно искать погрешность по формуле (15) с учетом замены соответствующих обозначений функции и аргументов:
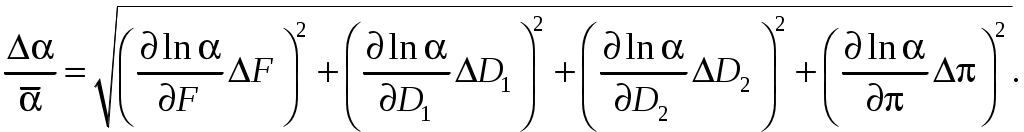
Прологарифмировав выражение (16), получим
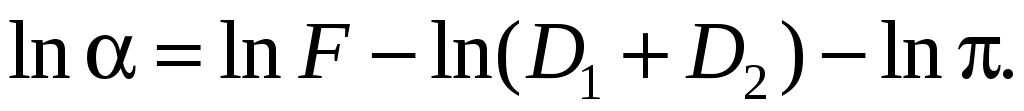
Находим частные производные
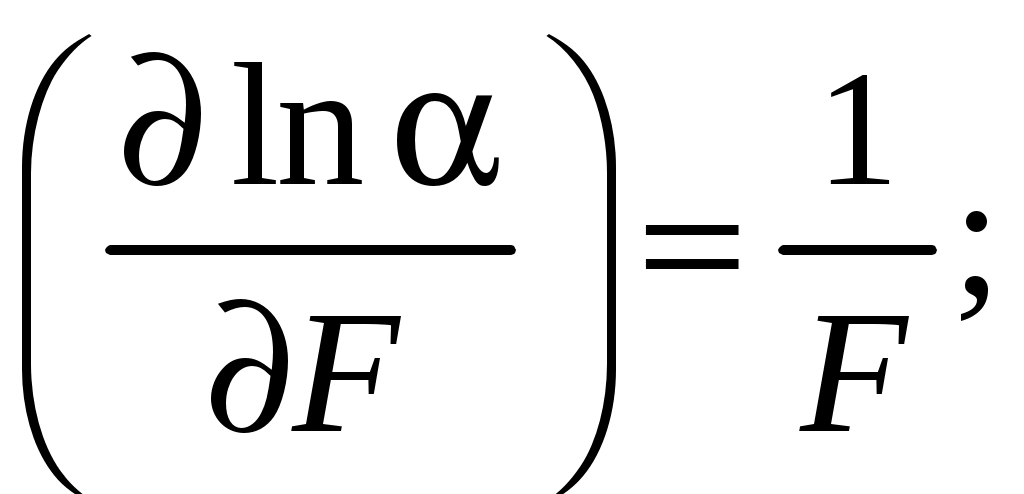
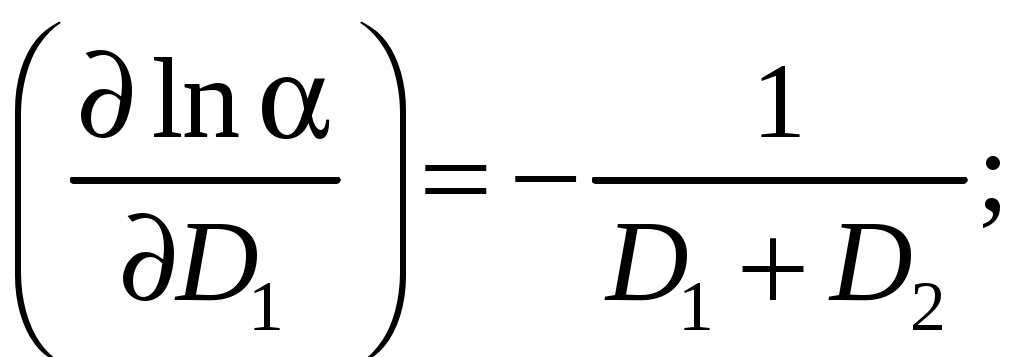
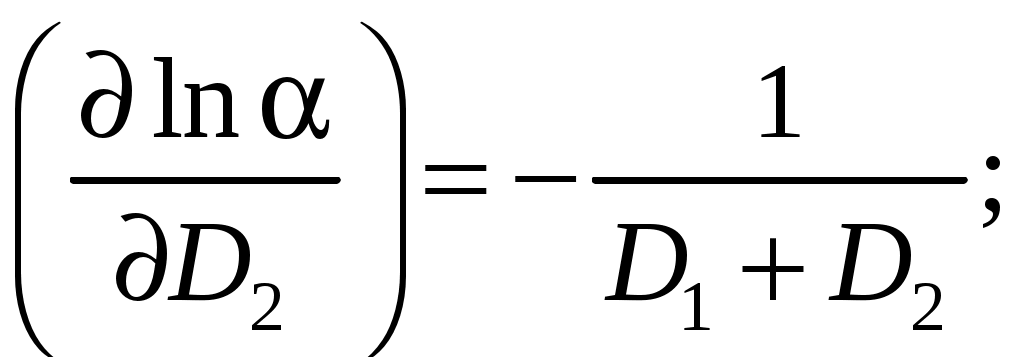
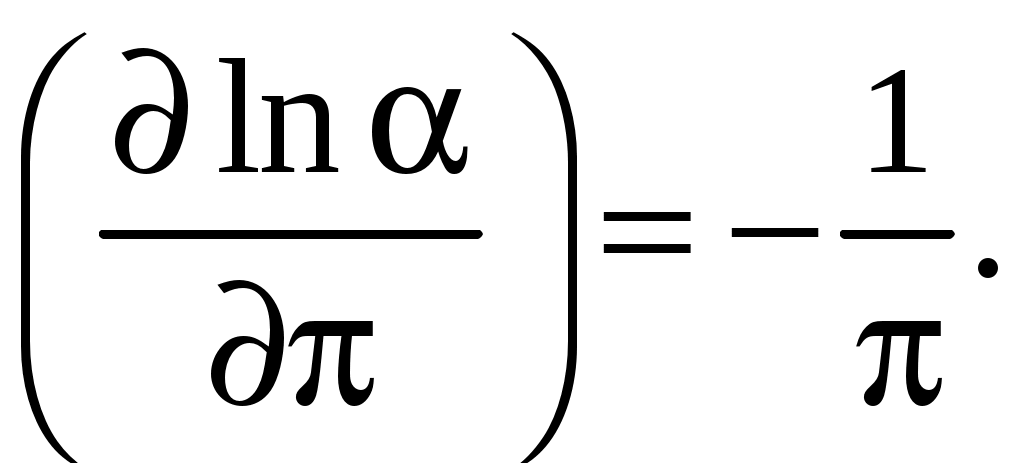
Выражение для расчета относительной погрешности:
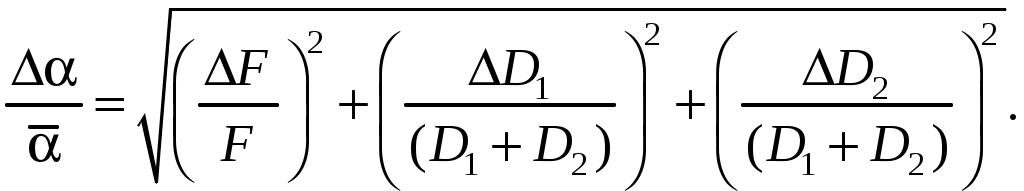
Отсутствие в данной формуле значения относительной погрешности числа обусловлено тем, что в настоящее время значение этого числа известно с высокой точностью.
обусловлено тем, что в настоящее время значение этого числа известно с высокой точностью.
Пример 2. В работе № 108 требуется определить отношение теплоемкостей (коэффициент Пуассона) воздуха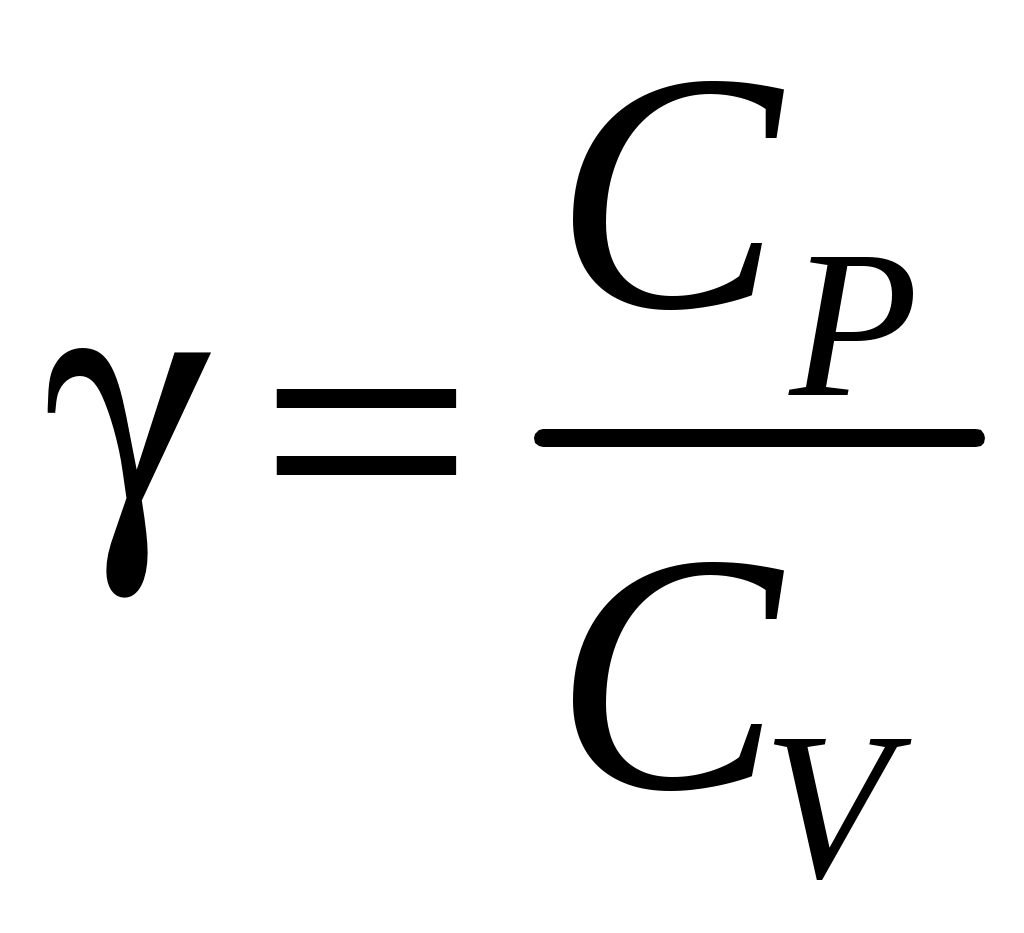 . Расчетная формула имеет вид
. Расчетная формула имеет вид
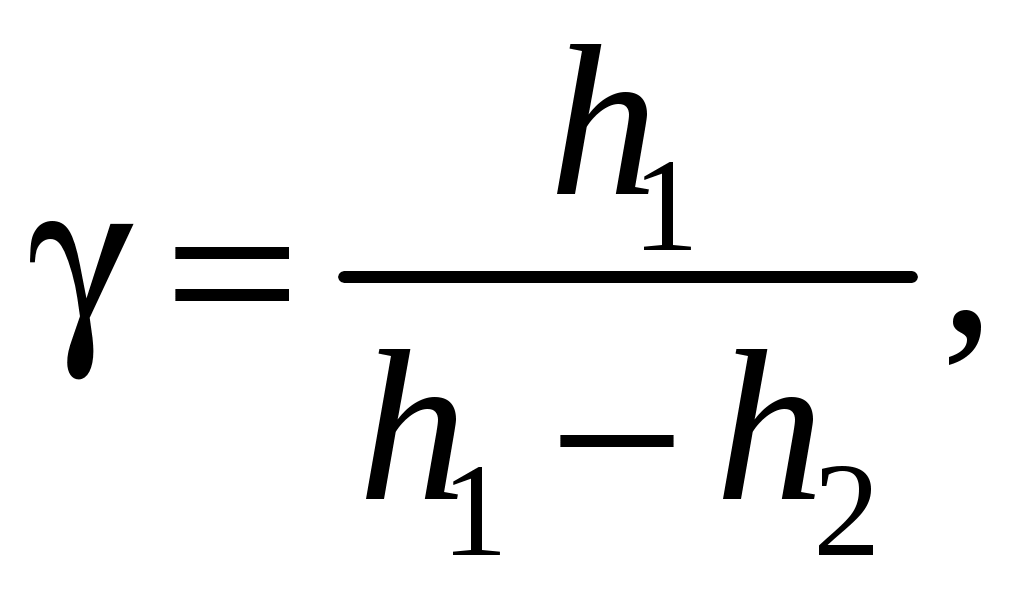 (17)
(17)
где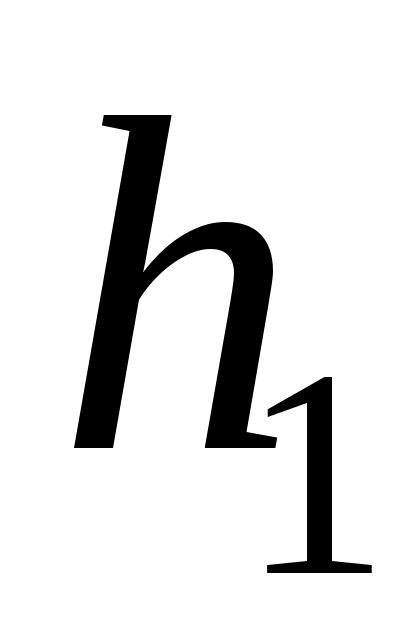 и
и 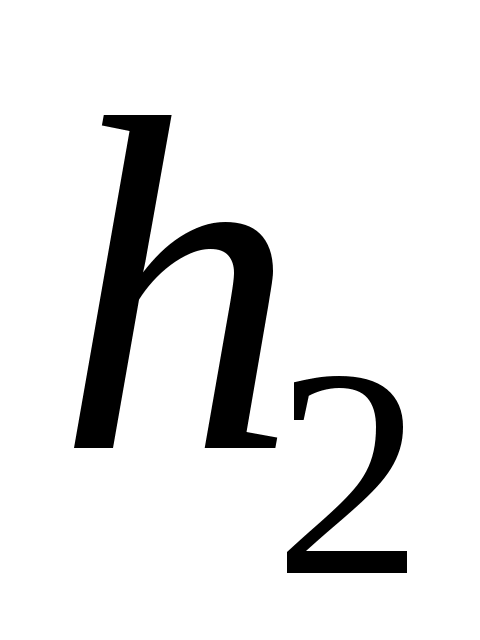
– разности уровней жидкости (воды) в манометре для некоторых двух состояний воздуха в сосуде.
Косвенные измерения в данном эксперименте являются невоспроизводимыми, поскольку, повторяя опыт, накачать и выпустить каждый раз одинаковое количество воздуха невозможно. Значения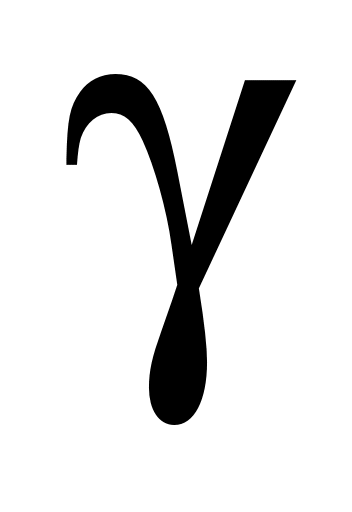 вычисляются в каждом наблюдении по результатам прямых измерений величин
вычисляются в каждом наблюдении по результатам прямых измерений величин  и
и  , а затем обрабатываются как результаты прямых многократных измерений. Следовательно, доверительная погрешность
, а затем обрабатываются как результаты прямых многократных измерений. Следовательно, доверительная погрешность 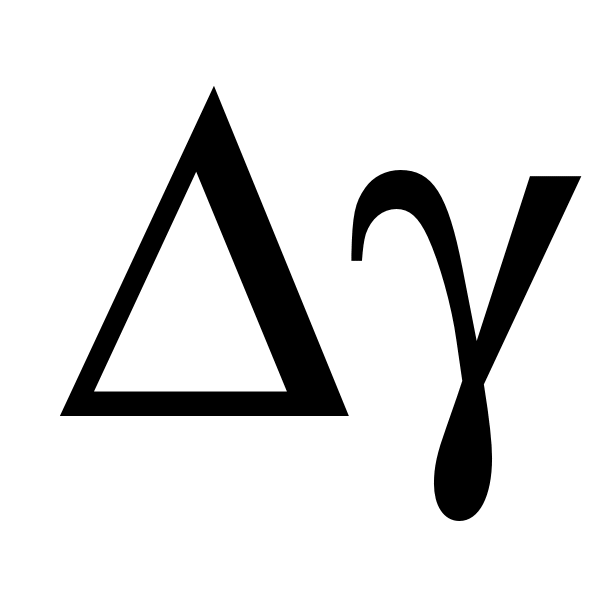 определяется как случайная по формуле
определяется как случайная по формуле
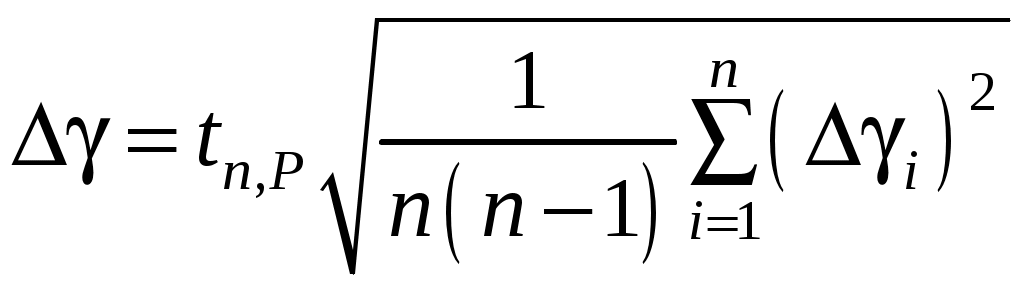 .
.
Пример 3. В лабораторной работе № 117 коэффициент жесткости пружины определяется по формуле
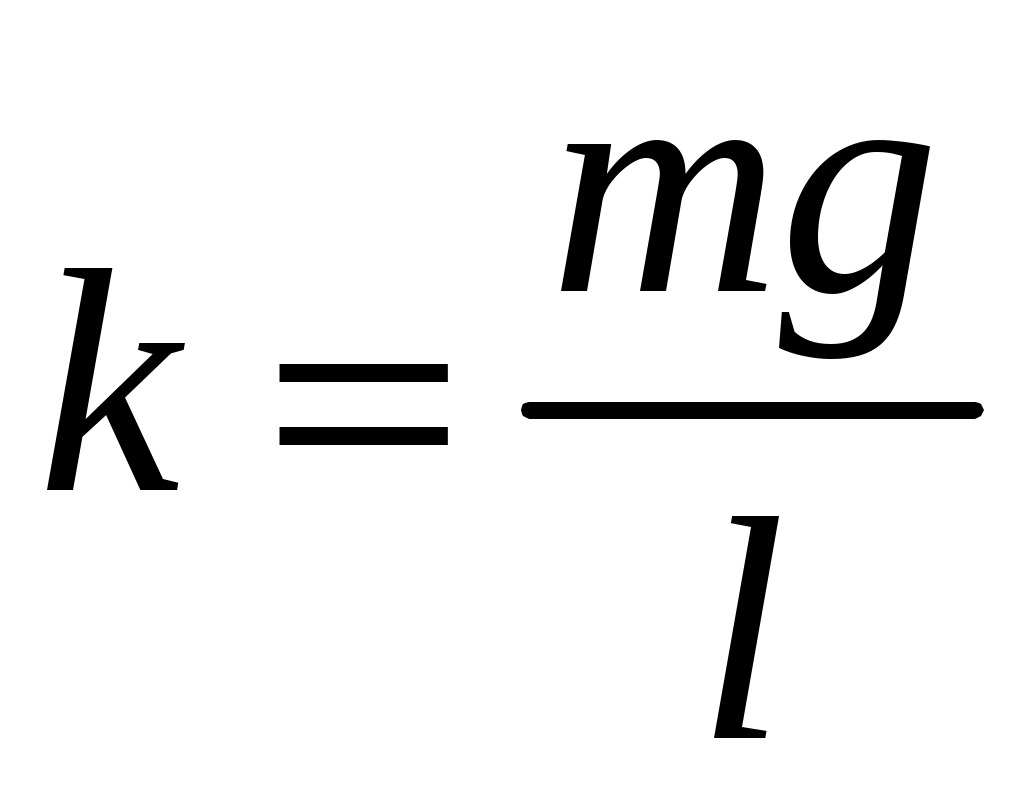 , (18)
, (18)
где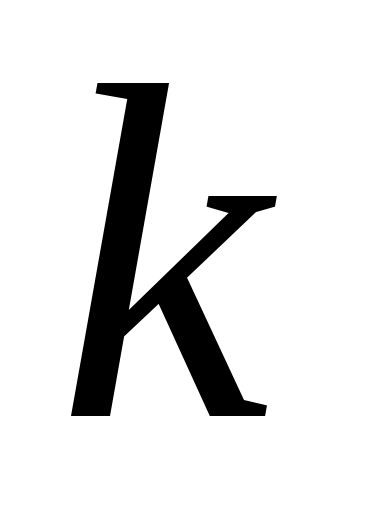 – коэффициент жесткости; m – масса груза; l – среднее удлинение пружины при увеличении массы груза на 50 г; g – ускорение свободного падения (на широте Санкт-Петербурга).
– коэффициент жесткости; m – масса груза; l – среднее удлинение пружины при увеличении массы груза на 50 г; g – ускорение свободного падения (на широте Санкт-Петербурга).
Воспользовавшись алгоритмом обработки результатов косвенных измерений в случае удобной для логарифмирования расчетной формулы, получим (см. пример 1) выражение
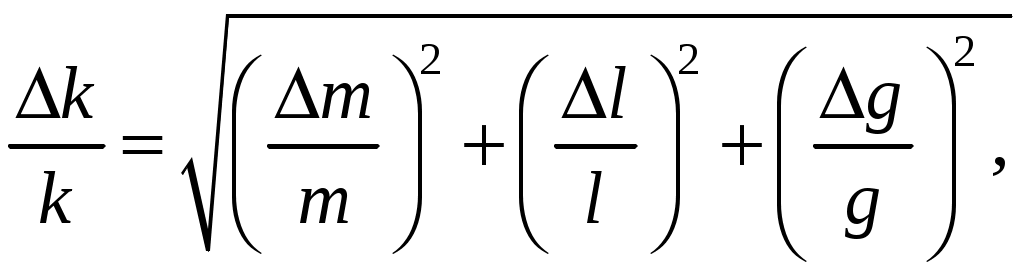
в котором погрешностью ускорения свободного падения можно пренебречь в силу ее малости.
В этой работе требуется также найти экспериментальное и расчетное значения периодов колебания груза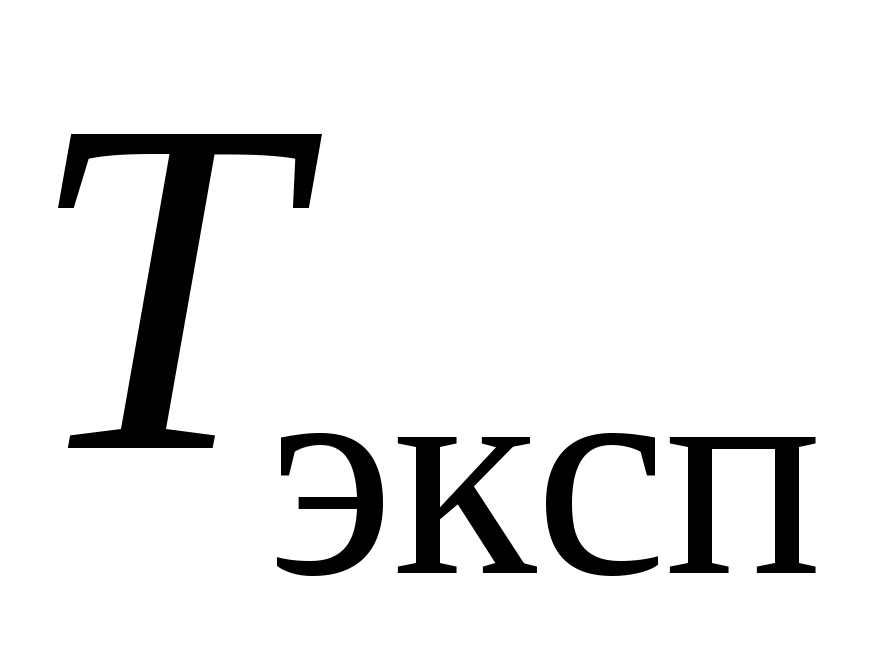 и
и 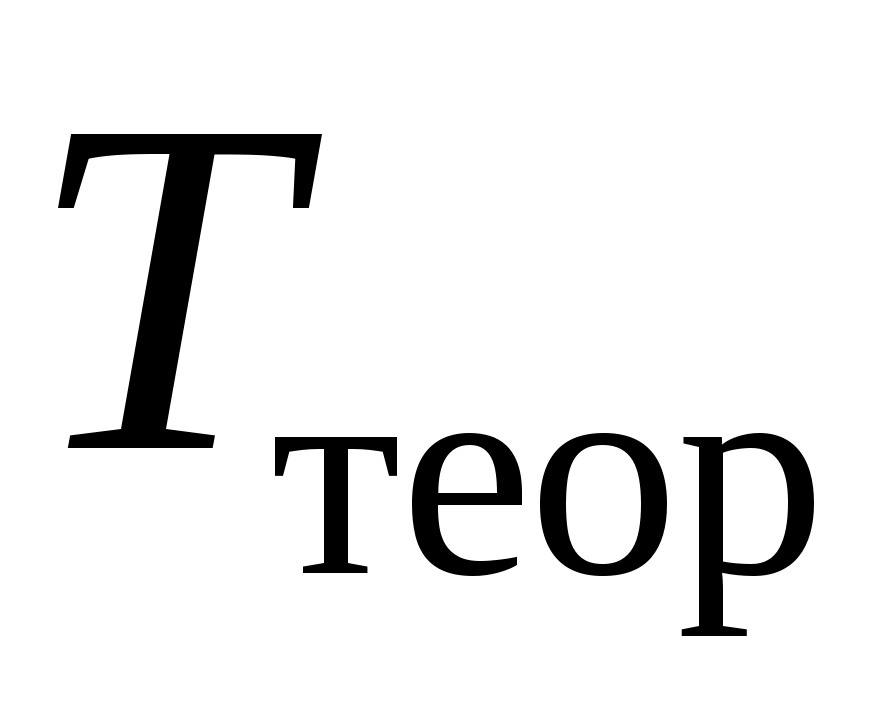 (масса груза задается преподавателем). Соответствующие формулы погрешностей имеют следующий вид:
(масса груза задается преподавателем). Соответствующие формулы погрешностей имеют следующий вид:
а) для расчетного значения периода колебания груза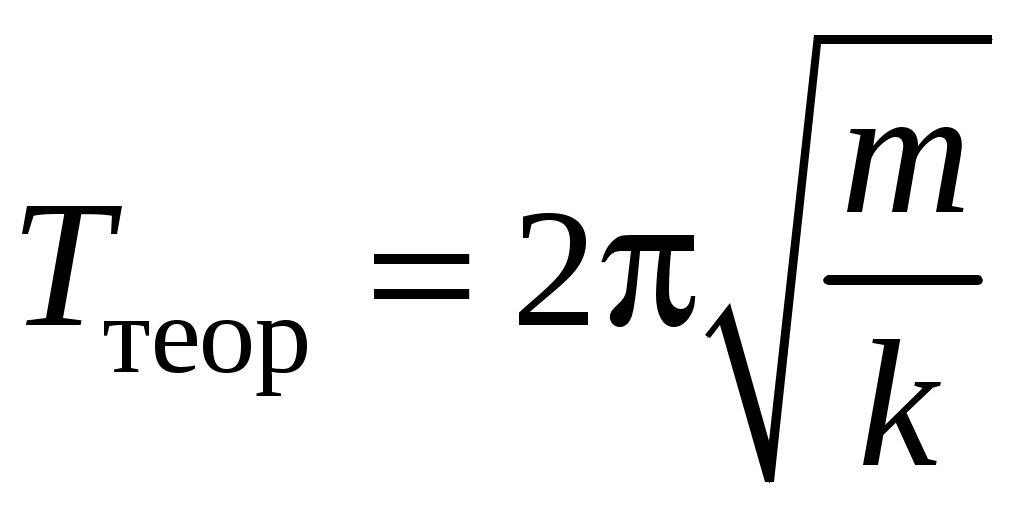
:
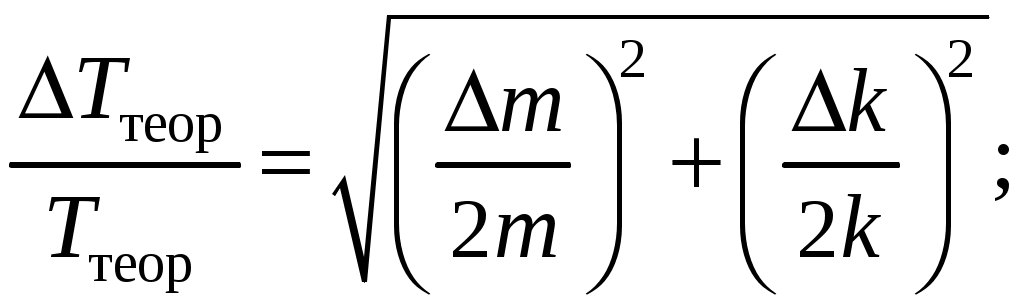
б) для периода колебаний, измеренного с помощью секундомера:
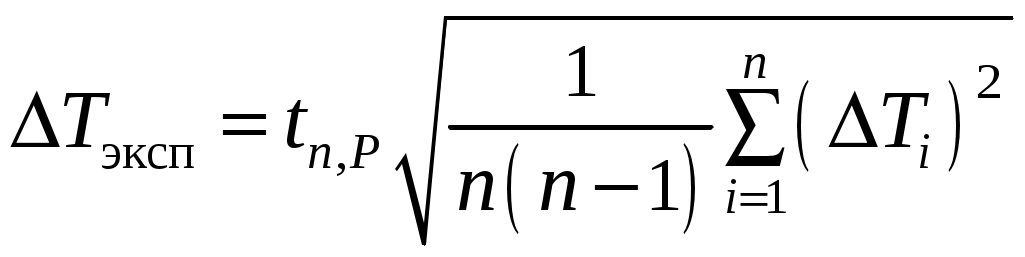 .
.
ОСНОВНЫЕ ПРАВИЛА ПОСТРОЕНИЯ ГРАФИКОВ
Важным методом обработки результатов опыта является представление их в виде графика. При минимальной обработке графики представляют результаты измерений в наиболее компактной форме с легкой обозримостью всего объема информации. Они позволяют проверить соответствие теории и результата эксперимента, выявить области изменения переменных, требующие более детального исследования.
Графический метод обработки результатов эффективен только при его грамотном применении, что предполагает овладение элементарными навыками работы с графическим материалом.
Выбор бумаги. Графики выполняют на миллиметровой бумаге. Размер листа для графика равен примерно 150×170 мм. При этом график достаточно масштабен, им удобно пользоваться (например, вклеивать или подшивать в лабораторный отчет). Очень удобны в этом отношении листы из «Блокнота для диаграмм».
Построение координатных осей. Графики принято строить в декартовой (прямугольной) системе координат, где по оси абсцисс откладывается переменная, выбранная за независимую (аргумент), а по оси ординат – функция. При нанесении осей следует оставить место для заголовка, поясняющих записей и полей для вклейки или подшивки в лабораторный отчет.
Выбор интервала изменения переменных и оцифровка шкал. Интервалы изменения переменных по обеим осям выбираются независимо друг от друга, так чтобы на графике была представлена лишь экспериментально исследованная область изменения переменных величин. Сам график при этом занимает все поле чертежа. Не следует стремиться к тому, чтобы начало координат (точка 0,0) обязательно поместилась на графике. Делать это разумно в тех случаях, когда одновременно существенно не увеличиваются размеры графика или когда эта точка является наиболее надежным результатом измерений. Например, при измерении силы тока I в зависимости от напряжения U точка (0,0) – очевидный и самый надежный результат этой зависимости.
Ценность графика во многом определяется удачным выбором масштаба. Рекомендуется выбирать удобные для восприятия и расчетов единицы масштаба шкал. Допустимы значения единиц масштаба, равные только

7. Округлив результат измерений и погрешность, записать окончательный результат в виде
НЕВОСПРОИЗВОДИМЫЕ КОСВЕННЫЕ ИЗМЕРЕНИЯ
Иногда при выполнении косвенных измерений невозможно повторить наблюдения в тождественных условиях относительно одного или нескольких аргументов измеряемой функции. Например, при измерении коэффициента вязкости жидкости в нее бросают металлические шарики (дробинки). Каждый из брошенных в жидкость шариков сразу же достать нельзя. Условия опытов, повторенных с разными шариками, не будут одинаковыми из-за различия размеров и формы шариков, различного состояния их поверхностей и т. д. В этом случае говорят, что косвенные измерения невоспроизводимы. Тем не менее коэффициент вязкости характеризует одну и ту же исследуемую жидкость и расчет должен давать близкие значения этого коэффициента для всех шариков.
Рекомендуется следующий порядок обработки результатов невоспроизводимых косвенных измерений.
1. Определить значение искомой функции
2. Каждое из определенных таким образом значений
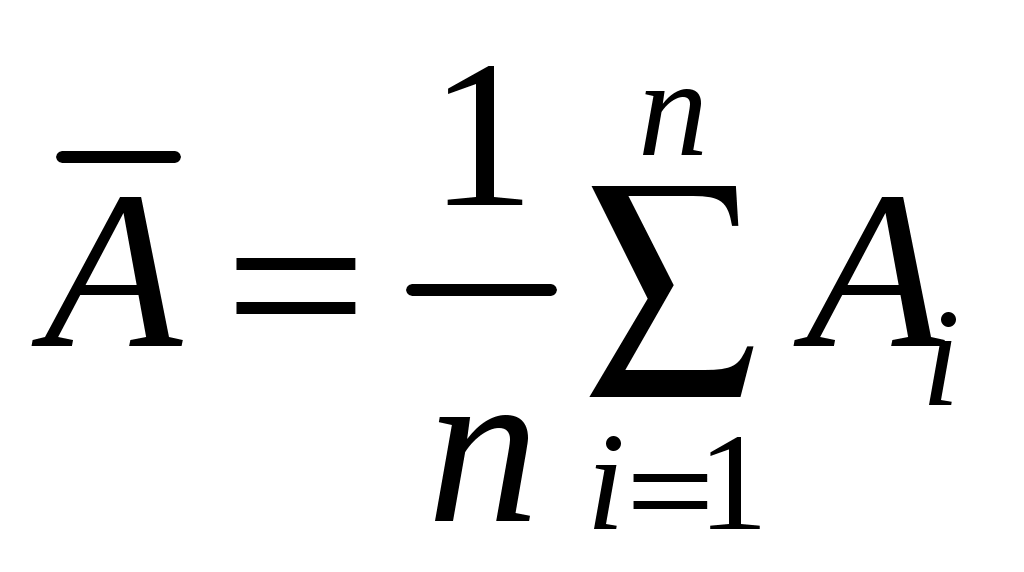 ,
,а погрешность вычисляется как случайная по формуле
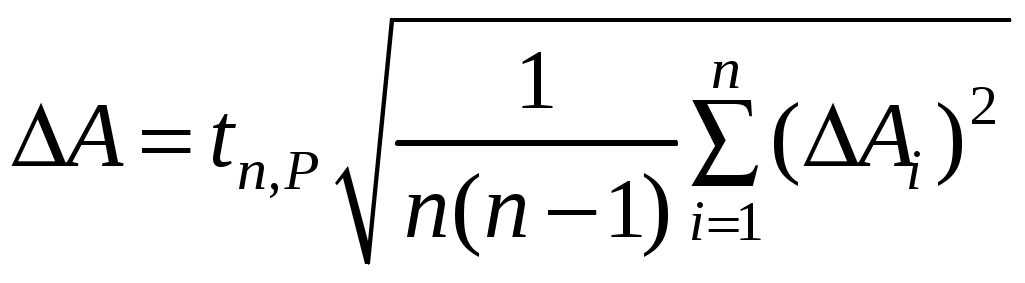 ,
,т. е. как при обработке результатов прямых многократных измерений.
ПРИМЕРЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ
Пример 1. В работе № 103 коэффициент поверхностного натяжения жидкости определяется по расчетной формуле
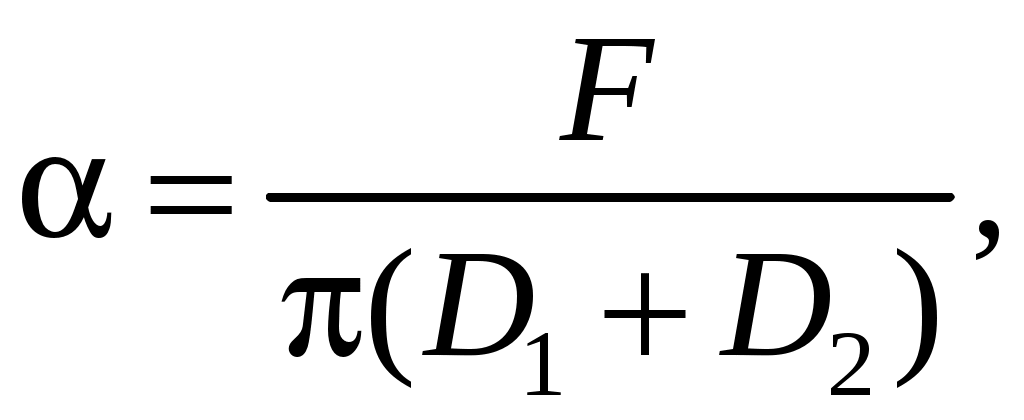 (16)
(16)где F – сила поверхностного натяжения;
Для получения расчетной формулы погрешности учтем, что выражение (16) относительно удобно для логарифмирования (содержит три множителя:
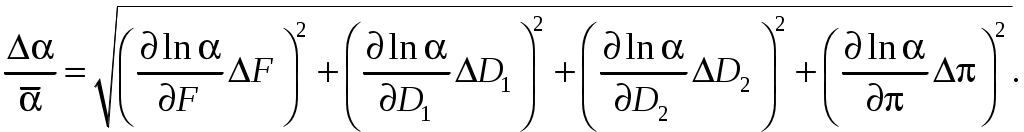
Прологарифмировав выражение (16), получим
Находим частные производные
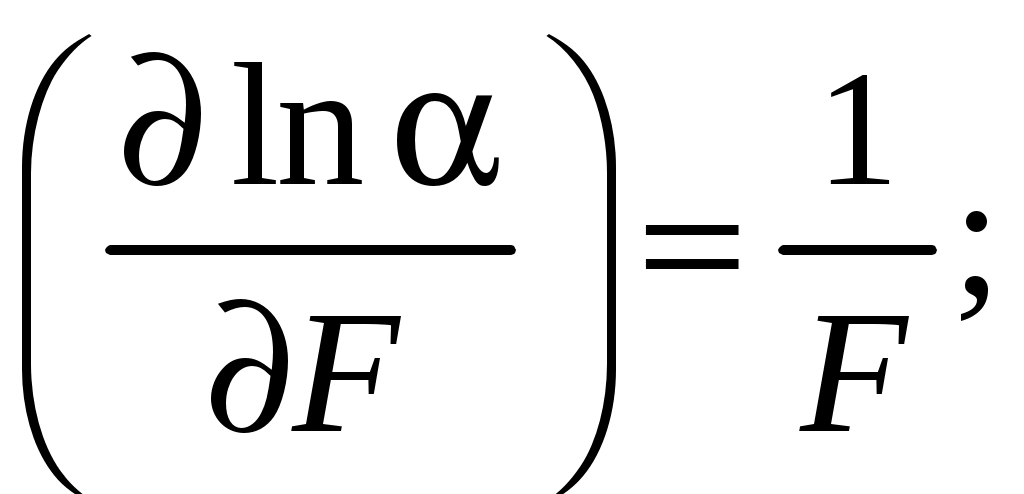
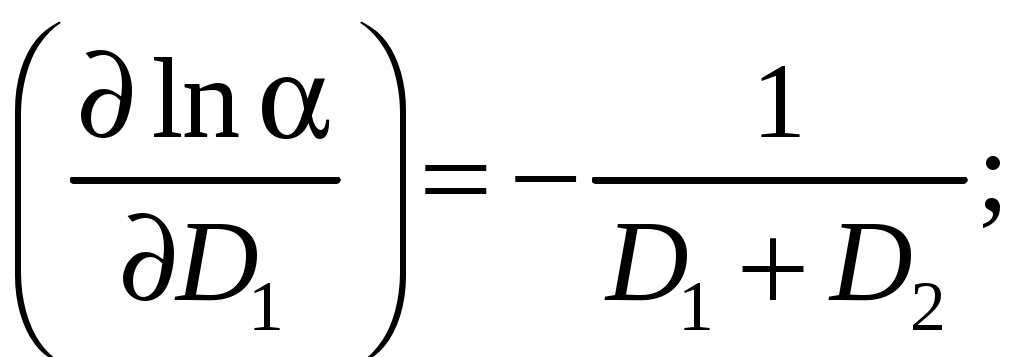
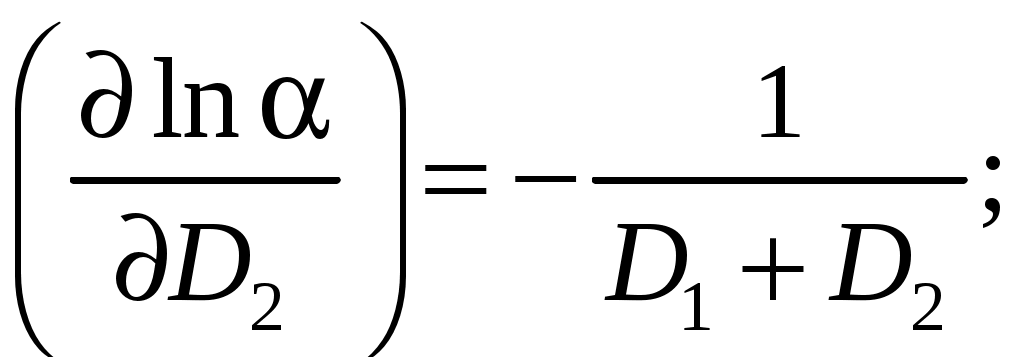
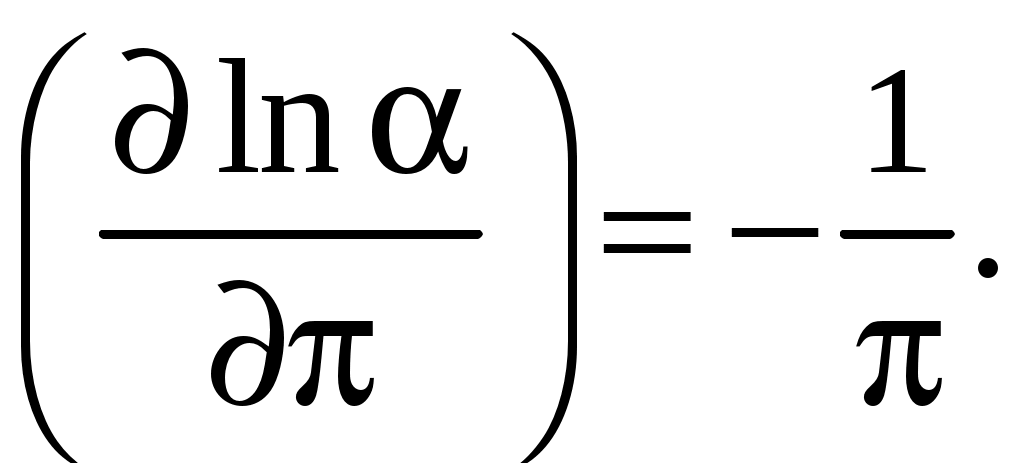
Выражение для расчета относительной погрешности:
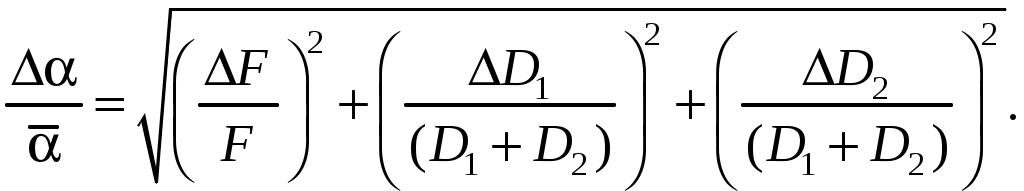
Отсутствие в данной формуле значения относительной погрешности числа
Пример 2. В работе № 108 требуется определить отношение теплоемкостей (коэффициент Пуассона) воздуха
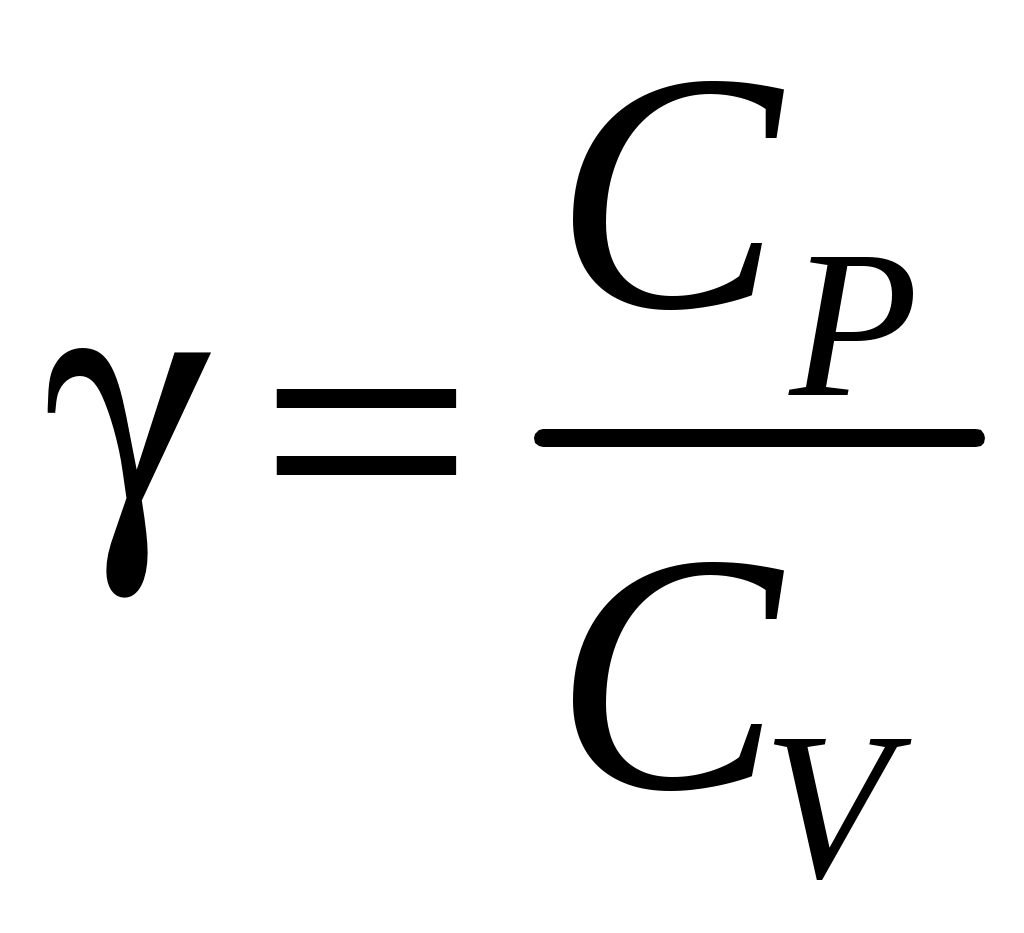 . Расчетная формула имеет вид
. Расчетная формула имеет вид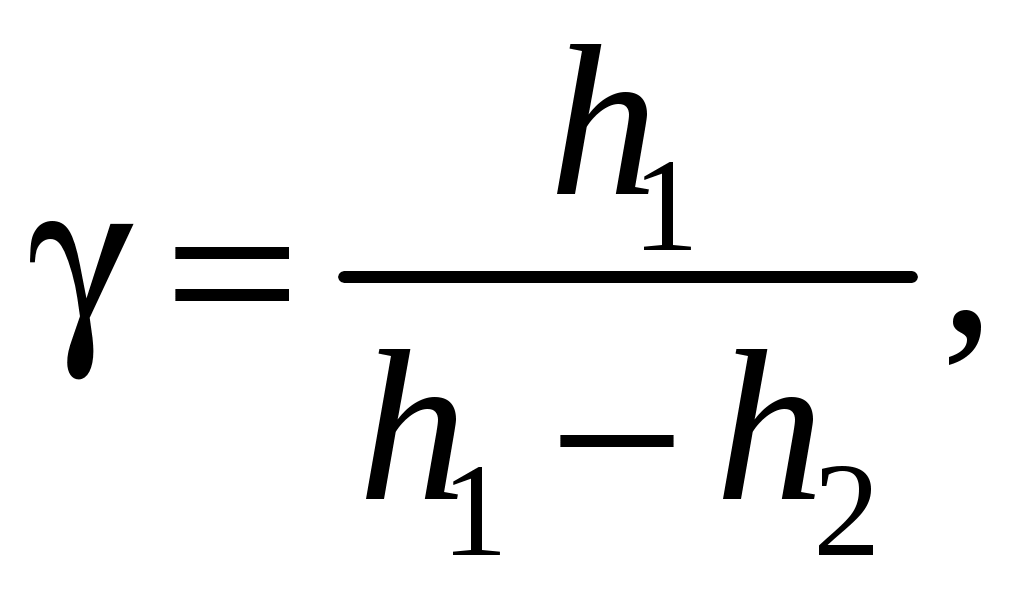 (17)
(17)где
– разности уровней жидкости (воды) в манометре для некоторых двух состояний воздуха в сосуде.
Косвенные измерения в данном эксперименте являются невоспроизводимыми, поскольку, повторяя опыт, накачать и выпустить каждый раз одинаковое количество воздуха невозможно. Значения
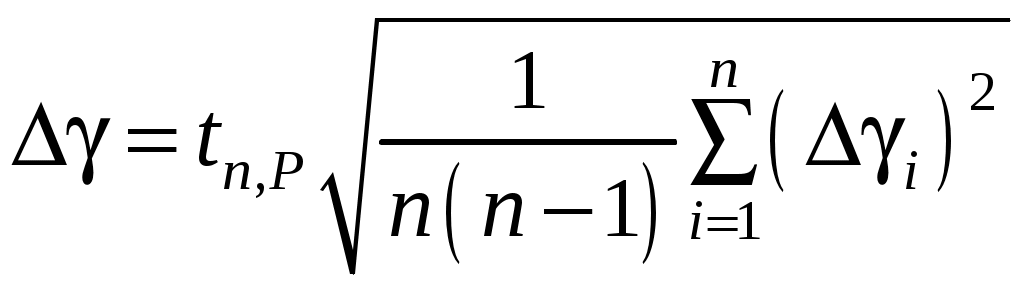 .
.Пример 3. В лабораторной работе № 117 коэффициент жесткости пружины определяется по формуле
где
Воспользовавшись алгоритмом обработки результатов косвенных измерений в случае удобной для логарифмирования расчетной формулы, получим (см. пример 1) выражение
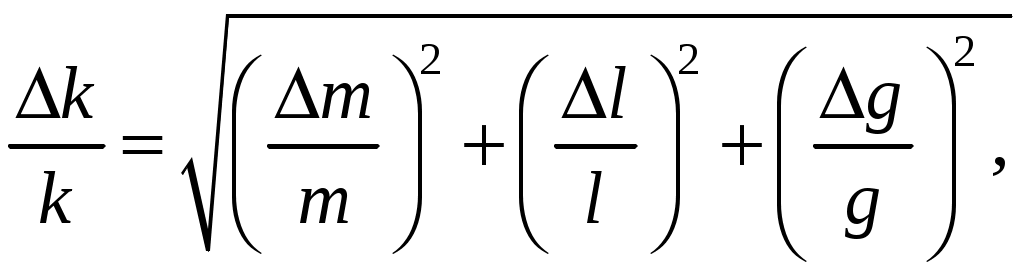
в котором погрешностью ускорения свободного падения можно пренебречь в силу ее малости.
В этой работе требуется также найти экспериментальное и расчетное значения периодов колебания груза
а) для расчетного значения периода колебания груза
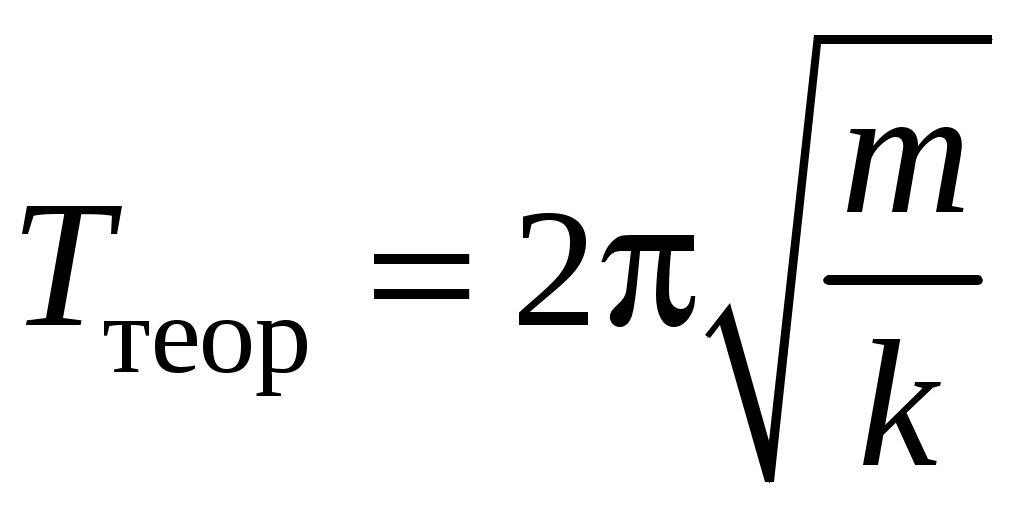
:
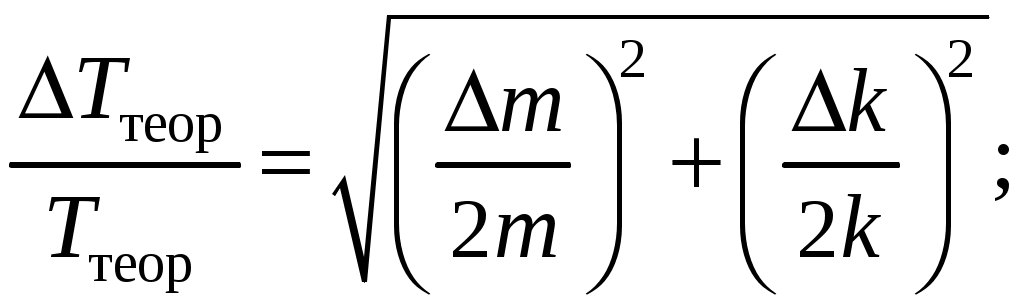
б) для периода колебаний, измеренного с помощью секундомера:
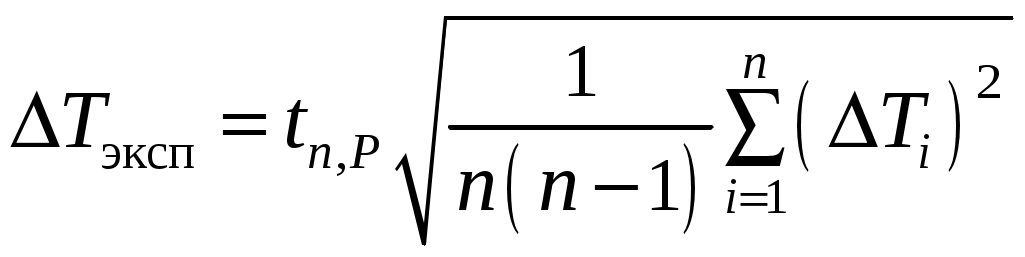 .
.ОСНОВНЫЕ ПРАВИЛА ПОСТРОЕНИЯ ГРАФИКОВ
Важным методом обработки результатов опыта является представление их в виде графика. При минимальной обработке графики представляют результаты измерений в наиболее компактной форме с легкой обозримостью всего объема информации. Они позволяют проверить соответствие теории и результата эксперимента, выявить области изменения переменных, требующие более детального исследования.
Графический метод обработки результатов эффективен только при его грамотном применении, что предполагает овладение элементарными навыками работы с графическим материалом.
Выбор бумаги. Графики выполняют на миллиметровой бумаге. Размер листа для графика равен примерно 150×170 мм. При этом график достаточно масштабен, им удобно пользоваться (например, вклеивать или подшивать в лабораторный отчет). Очень удобны в этом отношении листы из «Блокнота для диаграмм».
Построение координатных осей. Графики принято строить в декартовой (прямугольной) системе координат, где по оси абсцисс откладывается переменная, выбранная за независимую (аргумент), а по оси ординат – функция. При нанесении осей следует оставить место для заголовка, поясняющих записей и полей для вклейки или подшивки в лабораторный отчет.
Выбор интервала изменения переменных и оцифровка шкал. Интервалы изменения переменных по обеим осям выбираются независимо друг от друга, так чтобы на графике была представлена лишь экспериментально исследованная область изменения переменных величин. Сам график при этом занимает все поле чертежа. Не следует стремиться к тому, чтобы начало координат (точка 0,0) обязательно поместилась на графике. Делать это разумно в тех случаях, когда одновременно существенно не увеличиваются размеры графика или когда эта точка является наиболее надежным результатом измерений. Например, при измерении силы тока I в зависимости от напряжения U точка (0,0) – очевидный и самый надежный результат этой зависимости.
Ценность графика во многом определяется удачным выбором масштаба. Рекомендуется выбирать удобные для восприятия и расчетов единицы масштаба шкал. Допустимы значения единиц масштаба, равные только