Таблица 5

Разбиение массива данных по ячейкам

№ п/п	Ячейки гистограммы ∆x, В	Число наблюдений в ячейке, ∆n	∆n/n
1	19,75–19,85	2	0,04
2	19,85–19,95	6	0,12
3	19,95–20,05	17	0,34
4	20,05–20,15	18	0,36
5	20,15–20,25	6	0,12
6	20,25–20,35	1	0,02

Распределим полученные значения величины x по ячейкам и числа результатов, отнесенных к соответствующим интервалам, запишем в третью колонку табл. 5. Поделив эти числа на общее число наблюдений , получим значения , которые занесем в четвертую колонку.

Гистограмму и кривую закона распределения следует нанести на миллиметровую бумагу, как это показано на рис. 3. По оси абсцисс принято откладывать измеряемую величину x, по оси ординат – числа измерений и величину . Масштаб удобно выбрать таким, чтобы единице измеряемой величины (или 10; 100 единицам; 0,1 единицы и т. д.) соответствовал 1 см на миллиметровой бумаге. Удобным является также масштаб, при котором 1 см соответствует 2 или 5 единицам.


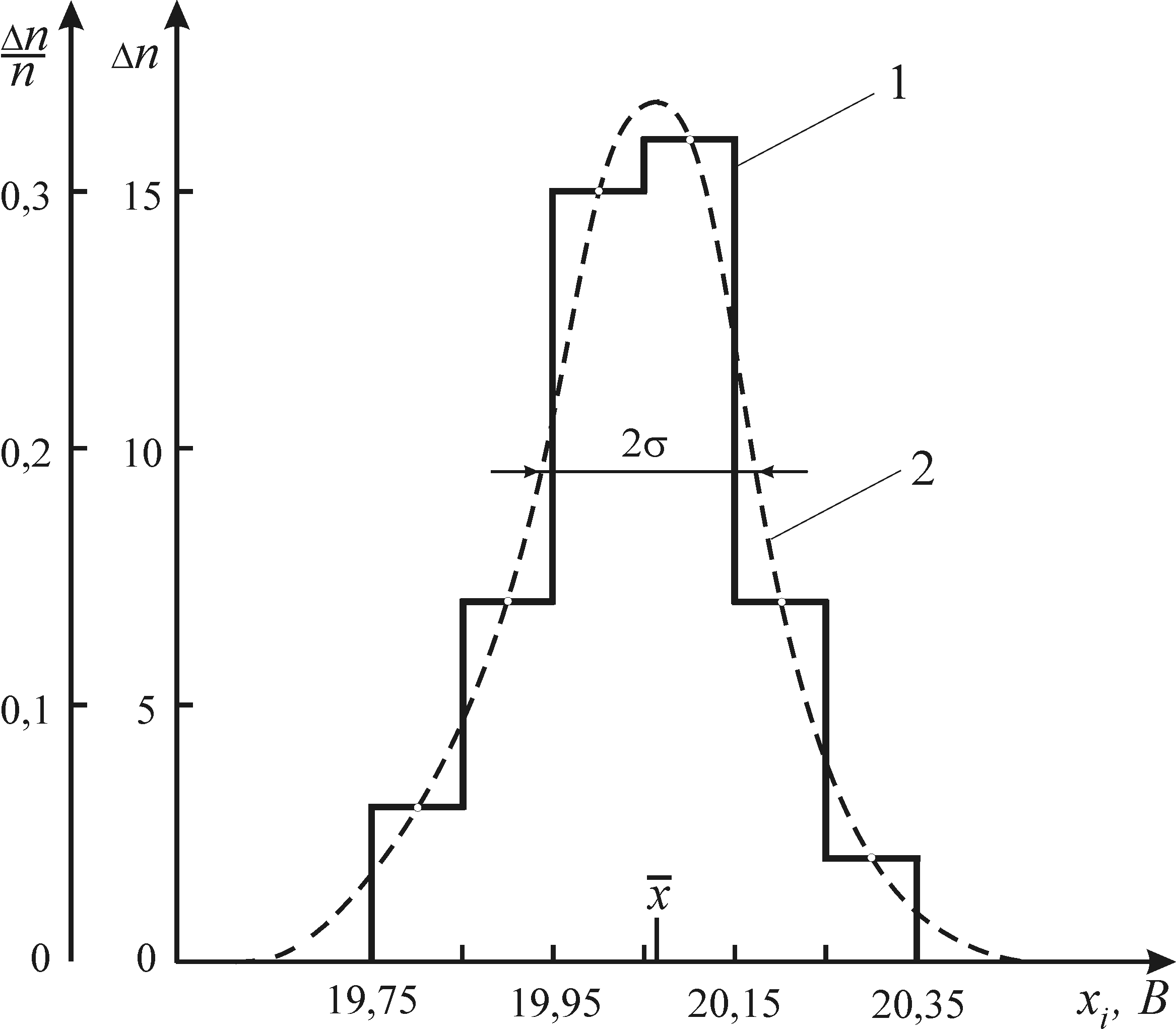
Рис. 3. Гистограмма экспериментальных значений (1)

и кривая закона распределения ∆n/n (2)

Напомним, что пересечение координатных осей не должно обязательно совпадать с нулевыми значениями аргумента и функции (необходимо полностью использовать все поле чертежа).

---

При построении кривой закона распределения через точки на ступеньках гистограммы (эти точки соответствуют середине интервалов ) следует наилучшим образом провести колоколообразную кривую. Поскольку значения функции в указанных точках имеют погрешности, совсем не обязательно, что все экспериментальные точки должны лежать на кривой.

Из рис. 3 видно, что на уровне 0,6 от максимального значения ширина кривой закона распределения , откуда следует, что , а значение , соответствующее максимальному значению ординаты, приближенно равно .
Описание установки

В данной работе требуется провести многократные измерения интервала времени с помощью механического (грубый прибор) и электронного секундомеров (более точный прибор).

Порядок выполнения работы

1. Прежде чем приступить к выполнению работы, необходимо ознакомиться с правилами пользования электронным секундомером. Соответствующая инструкция выдается лаборантом.

2. Получить у лаборанта механический секундомер. Интервал времени задается преподавателем.

3. С разрешения преподавателя включить тумблер электронного секундомера «Сеть» и дать прибору прогреться в течение 3–5 минут.

4. Измерить промежуток времени несколько раз механическим и электронным секундомерами, чтобы освоить технику измерений и исключить промахи, связанные с отсутствием опыта измерений (тренировочные измерения).

5. Выполнить многократные измерения заданного интервала времени электронным секундомером при условии одновременного запуска и остановки электронного и механического секундомеров 50–100 раз (по заданию преподавателя). Результаты опыта занести в табл. 6.

Таблица 6

---

Результаты опыта

№ п/п	Результаты отдельных измерений ti, с	Случайные отклонения от выборочного среднего ti – t, с
1
2
3
…
n

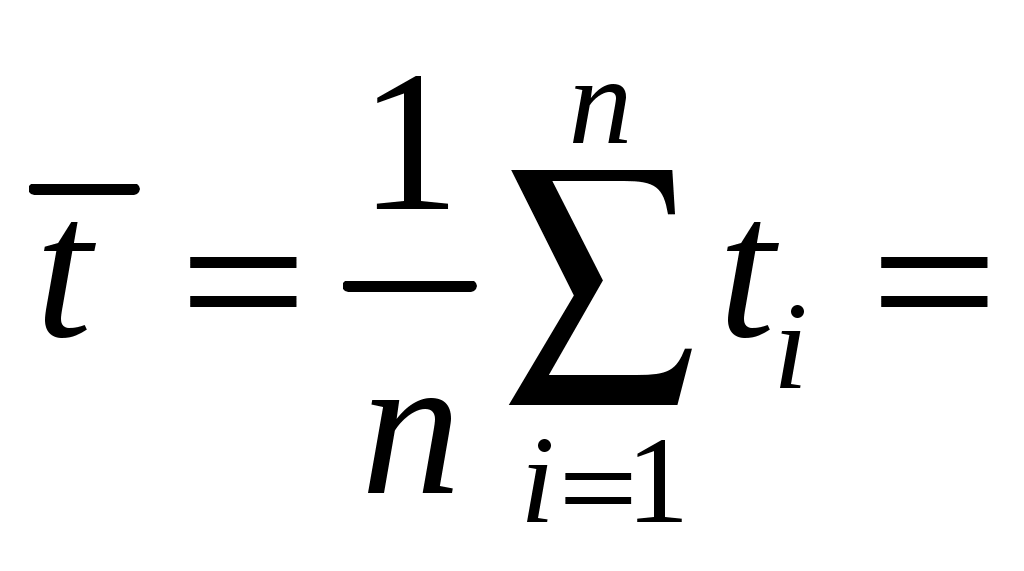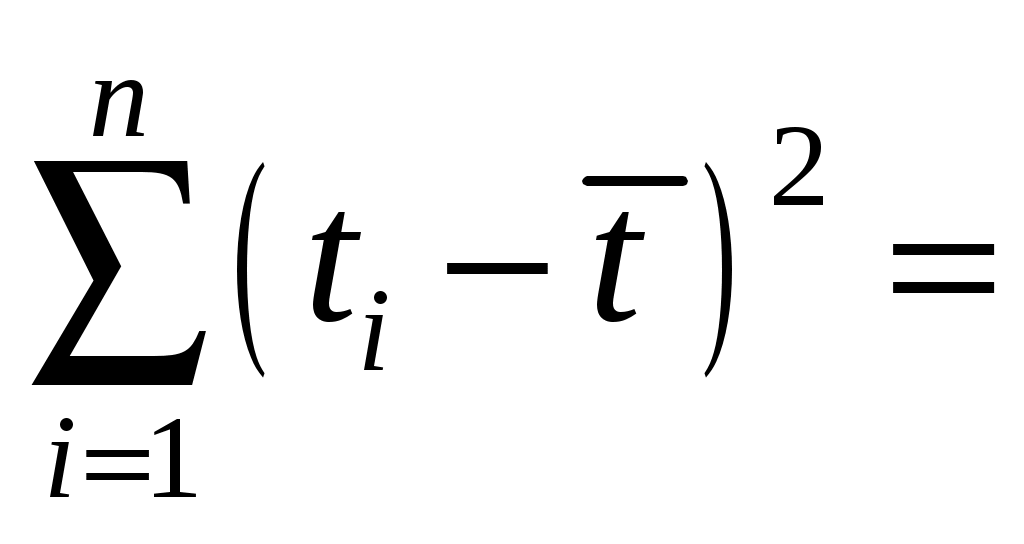Обработка результатов измерений

Задание 1. Исследование дрейфа.

Проанализировать изменение со временем значений измеряемой величины, для чего по данным табл. 6 построить график зависимости результатов наблюдений от порядкового номера наблюдения (рис. 2). В случае отсутствия дрейфа перейти к выполнению задания 2.

Задание 2. Статистический анализ выборки.

2.1. Определить выборочное среднее по формуле

.

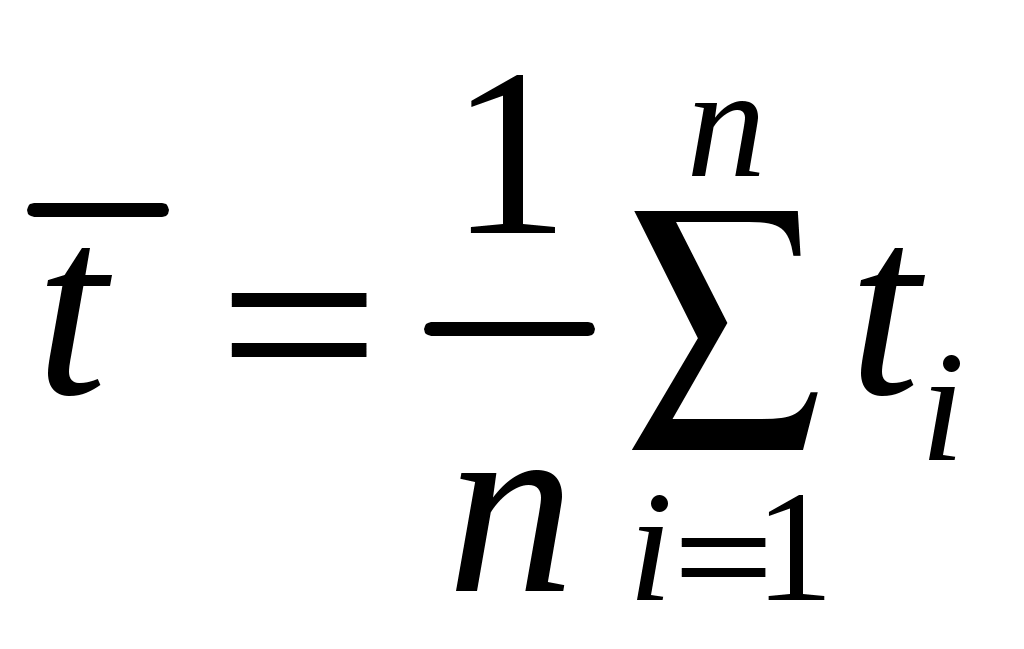2.2. Определить отклонения отдельных результатов наблюдений от среднего:

.

Записать в табл. 6 и проверить выполнение равенства .

2.3. Вычислить значения и сумму

---

, занести в табл. 6.

2.4. Рассчитать среднеквадратичную погрешность отдельного результата наблюдения:

.

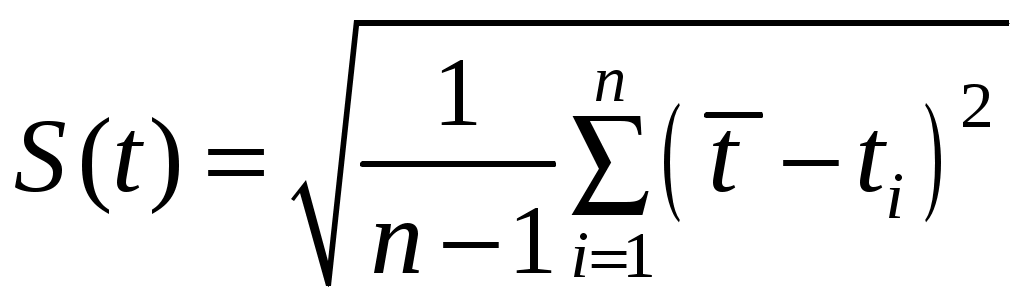2.5. Определить среднеквадратичную погрешность среднего арифметического результата измерений по формуле

.

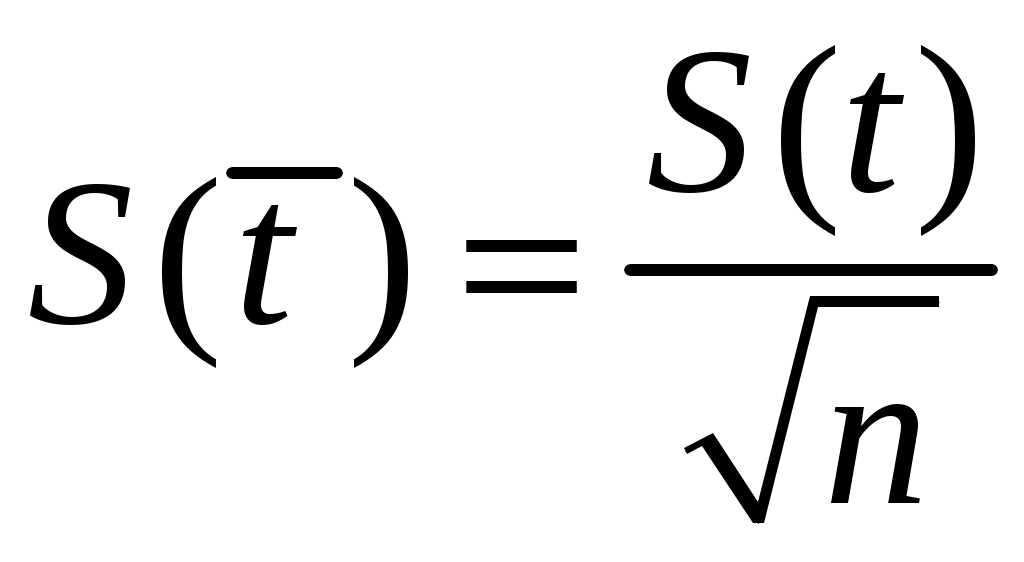2.6. Для заданных значений числа измерений n и доверительной вероятности найти по таблице коэффициент Стьюдента и вычислить случайную погрешность:

.

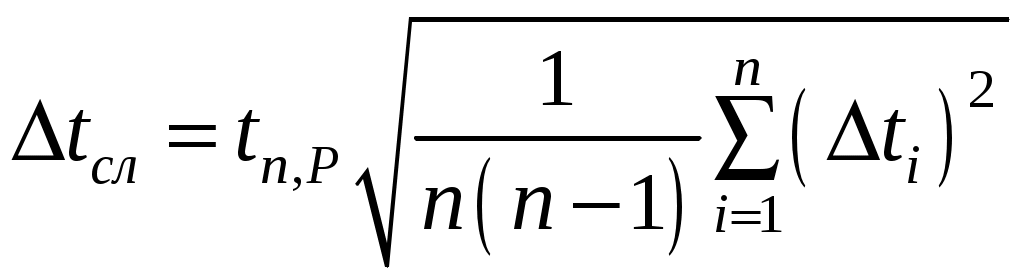2.7. Оценить приборную погрешность электронного секундомера по формуле (9). Проверить, что она меньше случайной более чем в два раза. В согласии с формулой (10) доверительную погрешность результата измерений приравнять к случайной:

.

2.8. Округлив погрешность и предварительный результат, записать окончательный результат измерений в виде

; ;

.

Задание 3. Оценка параметров закона распределения вероятностей с помощью гистограммы.

3.1. По результатам наблюдений составить таблицу, необходимую для построения гистограммы и кривой, описывающей закон распределения (см. табл. 5).

3.2. Построить гистограмму, кривую закона распределения и оценить по этой кривой значение величины среднеквадратичного отклонения σ.

3.3. Сравнить величину со значением σ, полученным по гистограмме и кривой закона распределения.

3.4. Записать выводы:

а) об отсутствии или наличии дрейфа;

б) о том, насколько экспериметально полученное значение длительности промежутка времени соответствует заданному;

---

в) о том, насколько полученная выборка соответствует гауссову закону распределения.

Контрольные вопросы

1. Какие измерения называются прямыми, косвенными, невоспроизводимыми косвенными?

2. Как рассчитывается доверительная погрешность при прямых многократных измерениях?

3. Почему при записи окончательного результата необходимо указывать доверительную вероятность?

4. Доверительная вероятность результата . Что это означает?

5. Какие погрешности называются систематическими, случайными, приборными?

6. Какая кривая называется гистограммой, законом распределения?

Библиографический список

1. Зайдель А. Н. Ошибки измерений физических величин : учеб. пособие / А. Н. Зайдель. – СПб. : Лань, 2005. – 112 с.

2. Деденко Л. Г. Математическая обработка и оформление результатов эксперимента / Л. Г. Деденко, В. В. Керженцев. – М. : МГУ, 1977.

3. Измерения физических величин и обработка результатов измерений : метод. указания к лабораторной работе № 100. – СПб., 2000. – 30 с.

4. Руководство к лабораторным занятиям по физике / Под ред. Л. Л. Гольдина. – М. : Наука, 1973.

ПРИЛОЖЕНИЕ

1. Подготовка к выполнению лабораторной работы

В течение семестра каждый студент должен выполнить предусмотренное учебным планом число лабораторных работ. Лабораторные работы выполняются студентами только в часы, установленные расписанием. Каждый учащийся должен приходить на лабораторной занятие подготовленным: необходимо тщательно ознакомиться с методическим указаниями, проработать соответствующий теоретический материал по учебнику и подготовить бланк лабораторной работы ­– основу будущего отчета.

Выполнять работу разрешается только после допуска, который подготовленный студент получает после собеседования с преподавателем. Допуск фиксируется преподавателем в учебном журнале и на титульном листе работы.

Если студент пропустил занятие или не получил допуск, то на следующем лабораторном занятии ему следует выполнять очередную по графику работу, а пропущенную сделать на итоговом занятии.

2. Правила оформления отчета о лабораторной работе

Отчет о лабораторной работе оформляется в рукописном виде индивидуально каждым студентом на белой бумаге формата А4 с одной стороны листа.

---

Смотрите также файлы

• Решение Момент инерции шара радиуса R, относительно оси, проходящей через его центр определяется по формуле (1).docx

• Развитие пенсионных систем в развитых странах мира и России. Абдуллина Алия.pptx

• Методические рекомендации по написанию практикума соответствуют рабочей программе дисциплины Административное право и Административнопроцессуальное право.pdf

• Каковы рекомендации врача.doc

• 1. зачетные соревнования на учебных занятиях.docx