Файл: Федеральное агентство железнодорожного транспорта Федеральное государственное бюджетное.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 66
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
одной, двум или пяти единицам измеряемой величины, умноженным на порядковый множитель 10m, где m – положительное или отрицательное целое число (порядок величины).
Число оцифрованных делений на каждой оси должно быть минимально необходимым для ясного понимания шкалы и составляет обычно от 4 до 10. По оси x цифры пишутся под масштабными рисками, обозначение откладываемой величины и ее единица измерения указываются справа под осью. По оси y цифры пишутся слева от рисок, а обозначение соответствующей величины и единица измерения указываются вверху слева от оси. Стрелки на осях не ставятся. Порядковый множитель 10m следует включать в буквенное обозначение или использовать десятичные приставки к названиям единиц. Например, «I, мкА», «R, кОм», «t, 10–2 , с».
Ни в коем случае не следует отмечать и оцифровывать на осях экспериментальные значения аргумента и функции, а тем более проводить штриховые линии для помещения экспериментальных точек на поле графика. Изобилие линий резко ухудшает восприятие графической информации. Следует помнить, что на графике, прежде всего, должны выделяться экспериментальные точки – именно они являются главным результатом работы экспериментатора.
Нанесение экспериментальных точек и их погрешностей. Экспериментальные точки нужно наносить на график точно и аккуратно, отмечая их кружками (квадратами, треугольниками, крестиками). Полезно применять разные знаки для разных кривых, если они изображаются на одном графике. Погрешности на графиках, когда это позволяет масштаб, можно указывать для одной или обеих измеряемых величин в виде отрезков, полудлина которых равна доверительной погрешности. Исключение составляют случаи, когда по одной из осей откладываются величины, известные точно (например, принимающие только целочисленные значения).
Обычно указание погрешностей либо загромождает график, либо их нельзя указать в данном масштабе (при точных измерениях). Поэтому допустимо иногда вообще не указывать погрешности или делать это для одной-двух точек. О точности измерений тогда можно весьма приближенно судить по разбросу точек относительно проведенной кривой.
Проведение кривой по экспериментальным точкам.
Экспериментальные точки соединяются карандашом плавной кривой так, чтобы они располагались примерно поровну и в среднем на равном удалении по обе стороны от кривой. Ни в коем случае не следует соединять экспериментальные точки на графике ломаной линией (от точки к точке). Обычно зависимости физических величин соответствуют гладким, плавно изменяющимся функциям без резких изломов и перегибов. Если же все точки последовательно соединить, то получится ломаная линия, которая не имеет ничего общего с истинной физической зависимостью. Это следует хотя бы из того факта, что форма полученной ломаной линии не будет воспроизводиться при повторных сериях измерений.
Проводимая на графике кривая не должна заслонять экспериментальные точки. Следует помнить, что именно точки являются результатом измерений, а кривая – лишь наше (не обязательно верное) толкование результата.
Оформление графиков. Графики должны быть снабжены заголовками и пояснениями, кратко и точно отражающими содержание графика. Обязательно указываются откладываемые по осям величины и их размерности. Если на одном графике располагается несколько кривых, то каждая из них должна быть четко обозначена цифрой или буквой, поясняемой в подписи к графику. Заголовок и пояснения располагают под графиком.
Лабораторная работа № 100
Измерение электронным секундомером интервалов времени,
задаваемых по механическому секундомеру
Цель работы – освоение алгоритма обработки результатов прямых многократных измерений, построение гистограммы экспериментальных значений определяемой величины и оценка параметров распределения Гаусса по кривой закона распределения.
Теоретическая часть
1. Измерение физических величин и графическое представление результатов измерений
При измерении физических величин в лабораторном практикуме из систематических погрешностей во внимание принимаются, как правило, только приборные как легко учитываемые. В таком случае в погрешность
определяемой величины входят две составляющие: случайная (статистическая)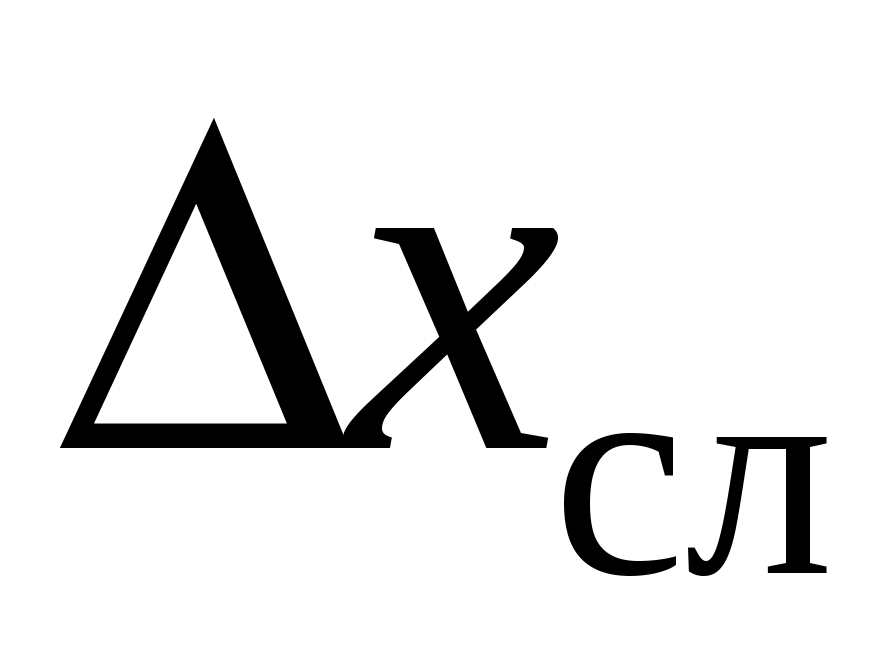 и систематическая (приборная)
и систематическая (приборная)  (предполагаем, что промахи отсутствуют):
(предполагаем, что промахи отсутствуют):
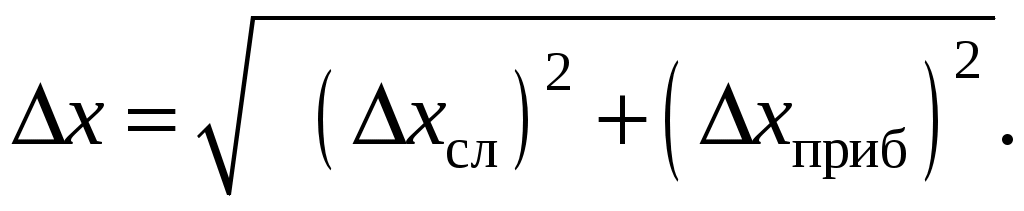
Если приборная погрешность значительно больше случайной, то при многократных измерениях практически получается один и тот же результат. Этот недостаток присущ в основном стрелочным приборам, подвижная часть которых, связанная со стрелкой, бывает настолько инерционной, что либо не реагирует на малые случайные отклонения, либо эти отклонения настолько малы, что их практически невозможно регистрировать. Такой прибор принято называть грубым. Точный прибор характеризуется меньшей систематической (приборной) погрешностью по сравнению со случайной, и поэтому на распределении полученных с его помощью результатов измерений сказывается случайный разброс. Точными приборами являются цифровые вольтметры, электронные секундомеры и весы, измерители сопротивлений, емкостей и индуктивностей и т. д. Полученные с их помощью n значений одной и той же измеряемой физической величины при неизменных контролируемых условиях следует обрабатывать как результаты прямых многократных измерений.
Если измерения выполняют с помощью грубого и точного приборов, то необходимо исключить просчеты (промахи), связанные с отсутствием навыков измерения. Особое значение это имеет для уменьшения различия в показаниях механического и электронного секундомеров, обусловленного реакцией исследователя и проявляющегося в недновременности как включения, так и выключения счетного устройства. После нескольких измерений промежутков времени (длительностью, например, 60 секунд) с помощью электронного секундомера удается их фиксировать с погрешностью в несколько сотых секунды. Просчетов на механическом секундомере в силу его большей приборной погрешности избежать значительно легче.
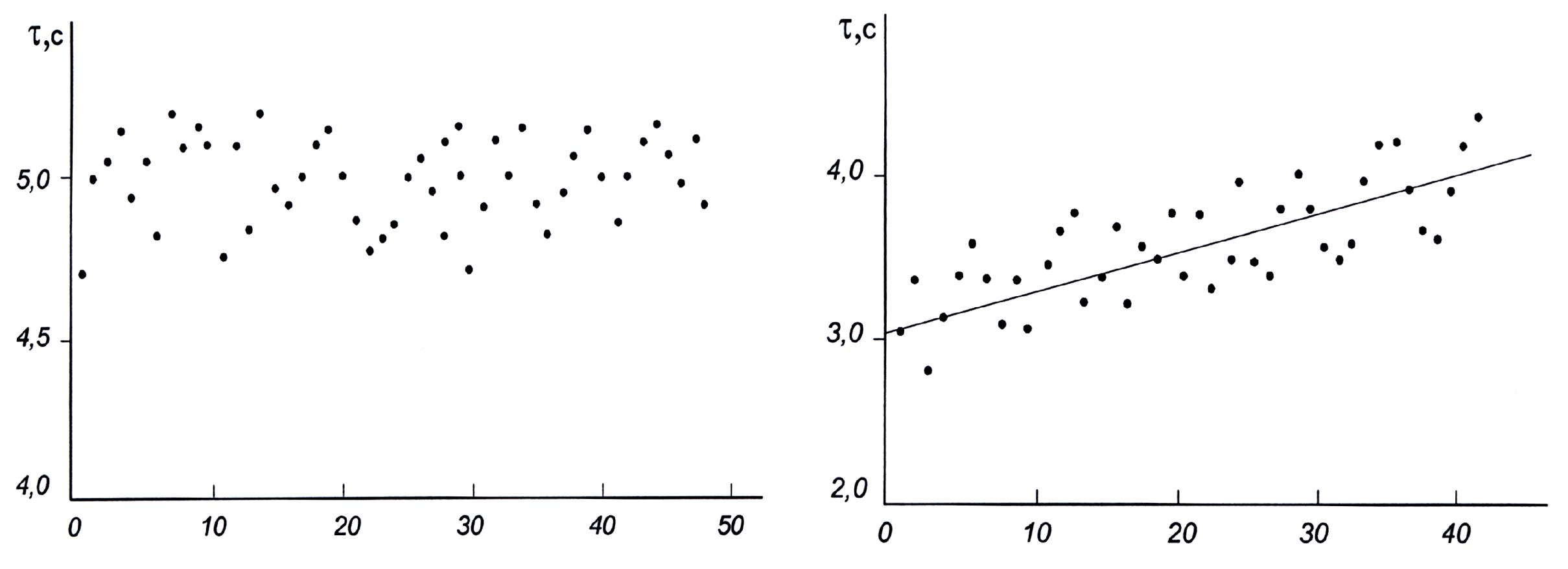
Перед проведением статистического анализа целесообразно проверить, не изменяются ли измеренные значения регулярным образом со временем. Такое изменение называется дрейфом. Для выяснения этого вопроса необходимо построить график зависимости результатов наблюдений от времени. Часто время заменяют последовательностью порядковых номеров
i отдельных наблюдений, которые наносят на горизонтальную ось. По вертикальной оси наносят значения измеряемой величины (рис. 2).
На рис. 2, а дрейф отсутствует, на рис.2. б результаты систематически увеличиваются с течением времени (с увеличением порядкового номера наблюдения i).
При наличии дрейфа следует установить, связан ли он с неисправностью прибора (в этом случае устранить ее или заменить прибор) или с закономерным изменением определяемой величины (здесь необходимо специальное исследование). При отсутствии дрейфа нужно построить экспериментальную гистограмму, показывающую, как часто получаются те или иные значения . Если
. Если 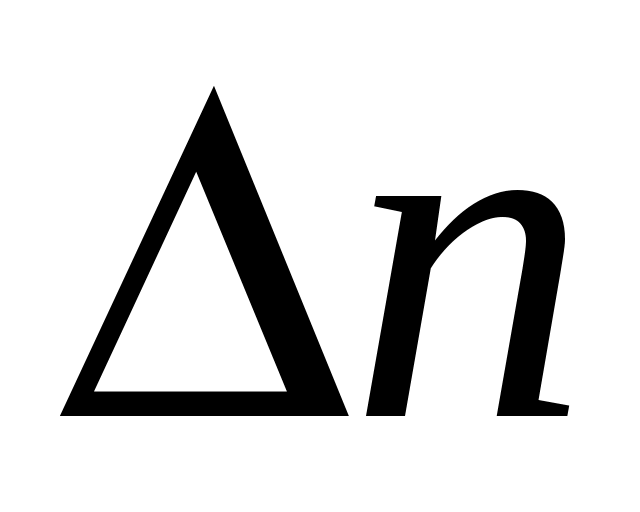 – число измерений, попадающих в любой из одинаковых интервалов (ячеек гистограммы), на которые разбивается весь диапазон значений определяемой величины, то величина
– число измерений, попадающих в любой из одинаковых интервалов (ячеек гистограммы), на которые разбивается весь диапазон значений определяемой величины, то величина 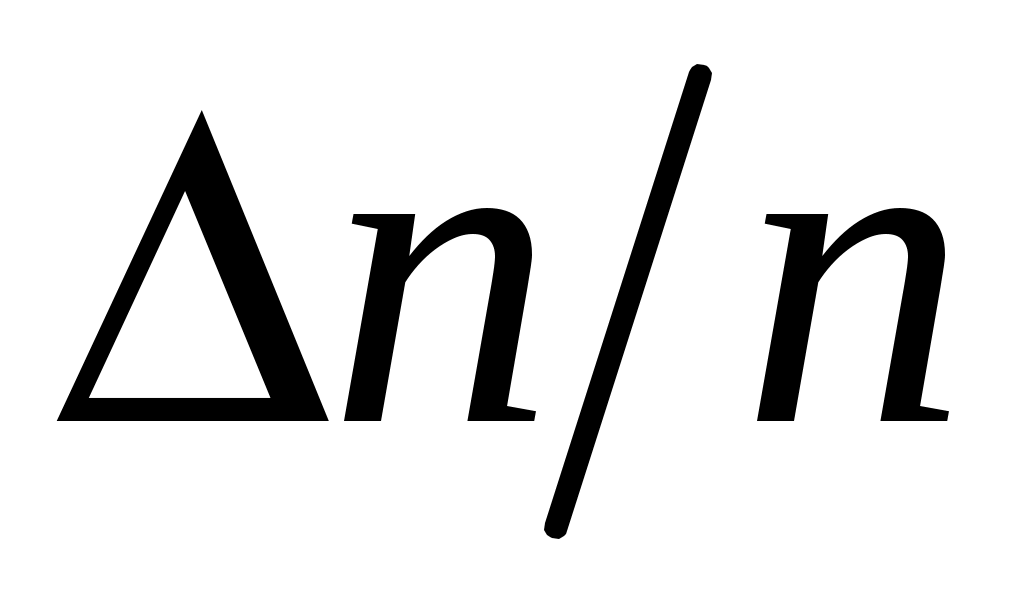 является оценкой вероятности того, что величина x находится в пределах ячейки. Кривая, наилучшим образом описывающая экспериментальное распределение вероятности, называется кривой закона распределения. В случае нормального распределения в качестве оценки
является оценкой вероятности того, что величина x находится в пределах ячейки. Кривая, наилучшим образом описывающая экспериментальное распределение вероятности, называется кривой закона распределения. В случае нормального распределения в качестве оценки  берут среднеквадратичное отклонение
берут среднеквадратичное отклонение  отдельного измерения (5). Относительная погрешность такой оценки зависит от числа измерений и при небольшом n она велика. При 50 измерениях относительная погрешность составляет приблизительно 22 %, поэтому достаточно сделать 40–50 измерений. Оценить величину
отдельного измерения (5). Относительная погрешность такой оценки зависит от числа измерений и при небольшом n она велика. При 50 измерениях относительная погрешность составляет приблизительно 22 %, поэтому достаточно сделать 40–50 измерений. Оценить величину  можно, не прибегая к формуле (5), а используя кривую закона распределения: величина параметра
можно, не прибегая к формуле (5), а используя кривую закона распределения: величина параметра  равна полуширине кривой на уровне 0,6 от ее максимального значения.
равна полуширине кривой на уровне 0,6 от ее максимального значения.
а)
б)

Рис. 2. Зависимость значений результатов измерения
от порядкового номера отсчета (от времени):
а – дрейф отсутствует; б – дрейф наблюдается;
точки – экспериментальные значения, прямые – аппроксимация точек
2. Пример построения гистограммы экспериментальных значений определяемой величины x и оценки параметров σ и x0 из кривой закона распределения
Пусть проведено 50 отсчетов величины напряжения, из которых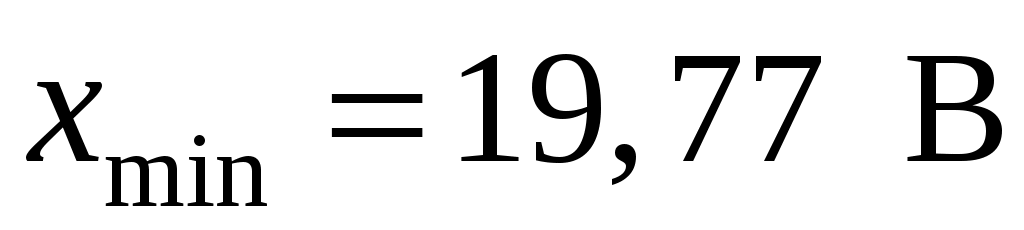 , а
, а 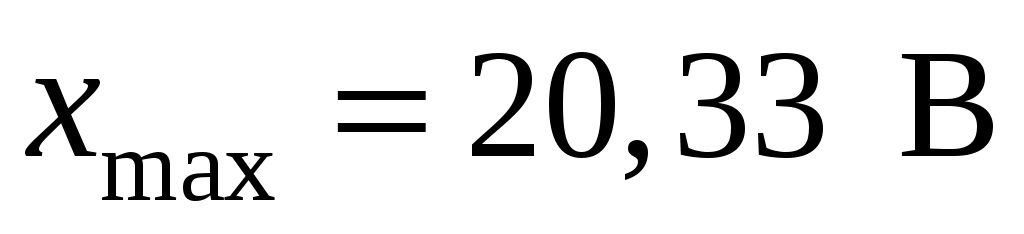 . Эти значения укладываются в диапазоне напряжений
. Эти значения укладываются в диапазоне напряжений 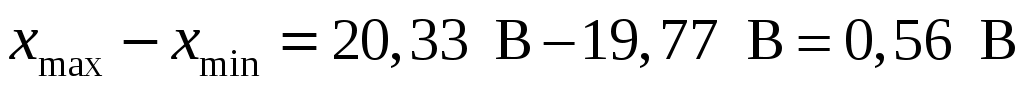 . Если принять, что в одну ячейку гистограммы попадает не менее четырех значений, то при общем числе наблюдений 50 весь диапазон величины x можно разбить не более чем на 50/4
. Если принять, что в одну ячейку гистограммы попадает не менее четырех значений, то при общем числе наблюдений 50 весь диапазон величины x можно разбить не более чем на 50/4  12 одинаковых интервалов или ячеек гистограммы.
12 одинаковых интервалов или ячеек гистограммы.
Учтем неравномерность распределения результатов наблюдений по всему диапазону. Это уменьшает число ячеек примерно в 1,5–2 раза. Возьмем 6 ячеек. Длина ячеек будет равна примерно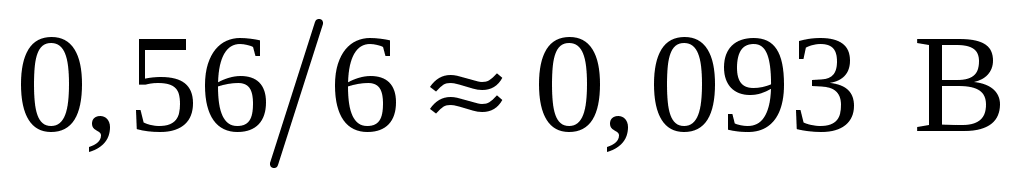 . Поскольку измеренные значения x содержат сотые доли, длина ячейки должна быть равной 0,09 или 0,10 В. Выбрав значение 0,09 В, мы уменьшим общую длину всех ячеек и потеряем часть измерений при построении гистограммы (
. Поскольку измеренные значения x содержат сотые доли, длина ячейки должна быть равной 0,09 или 0,10 В. Выбрав значение 0,09 В, мы уменьшим общую длину всех ячеек и потеряем часть измерений при построении гистограммы (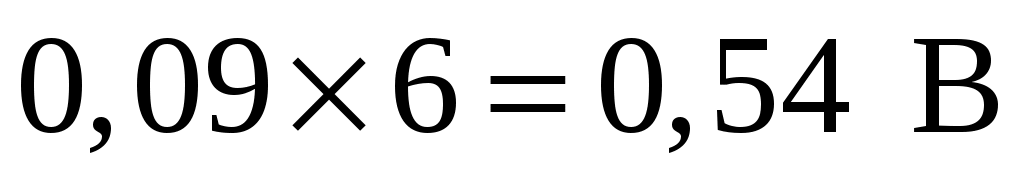 вместо
вместо 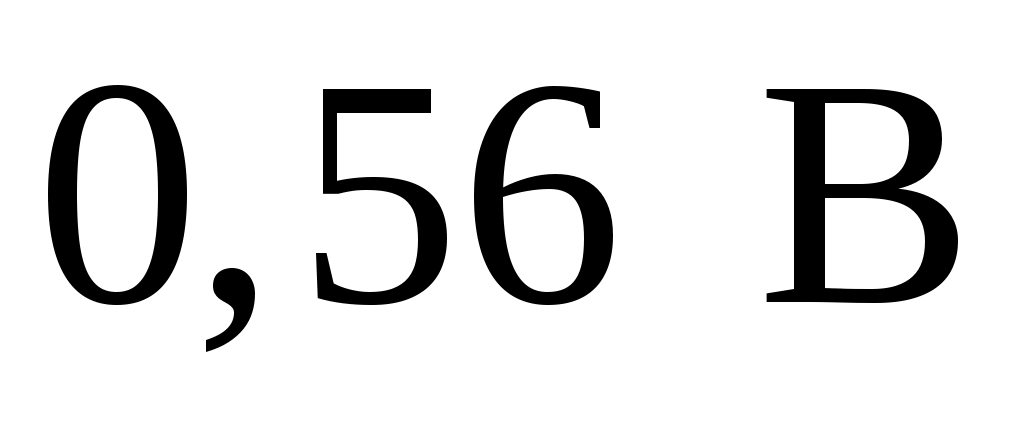 ). Поэтому следует несколько расширить диапазон значений x так, чтобы он включал в себя разность
). Поэтому следует несколько расширить диапазон значений x так, чтобы он включал в себя разность 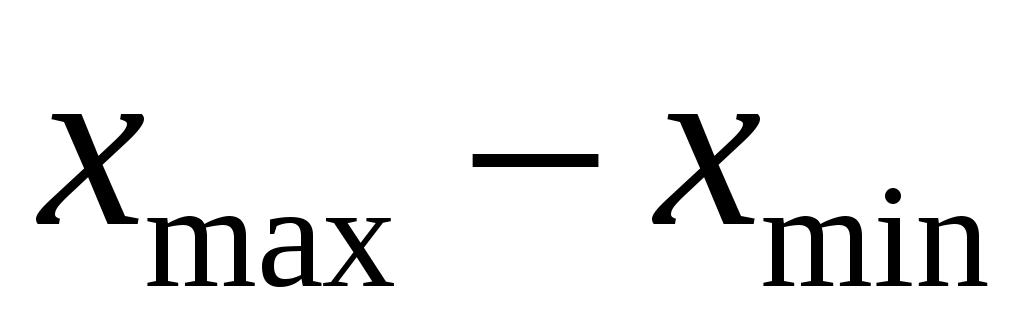 . В данном конкретном случае в качестве минимального целесообразно взять значение
. В данном конкретном случае в качестве минимального целесообразно взять значение 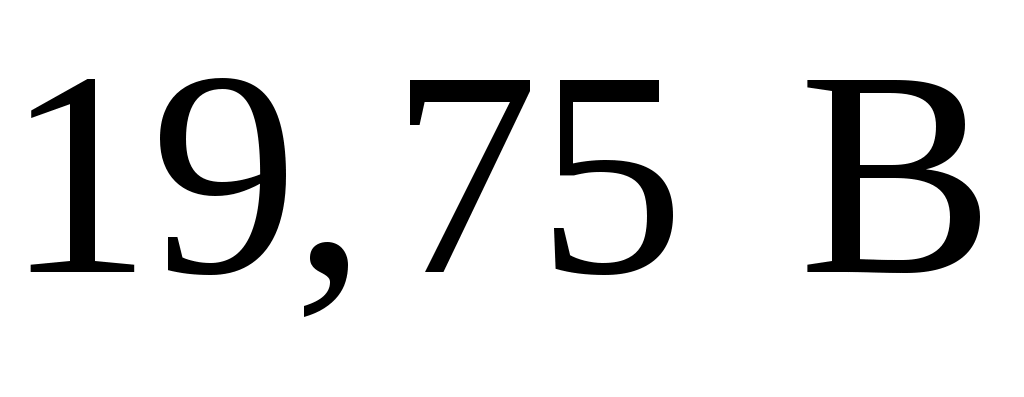 , а в качестве максимального –
, а в качестве максимального – 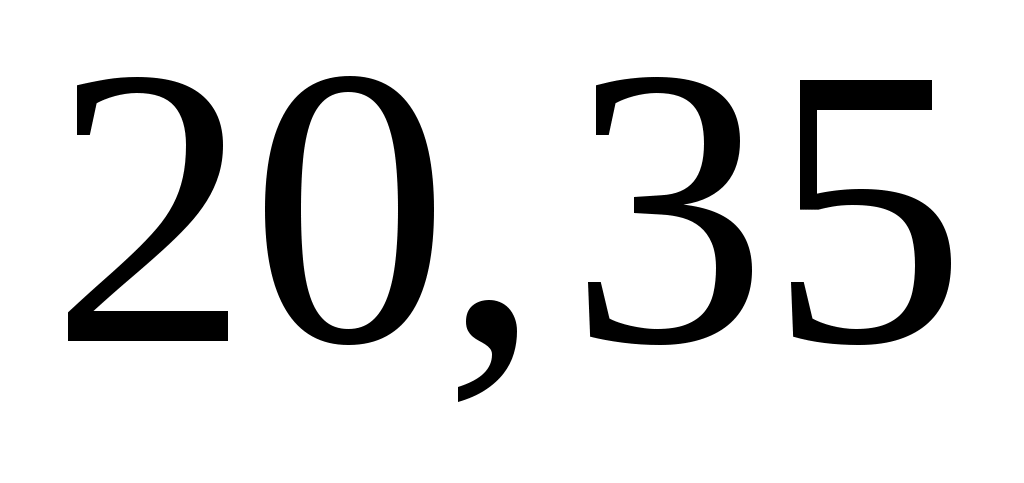 В, размер ячейки –
В, размер ячейки –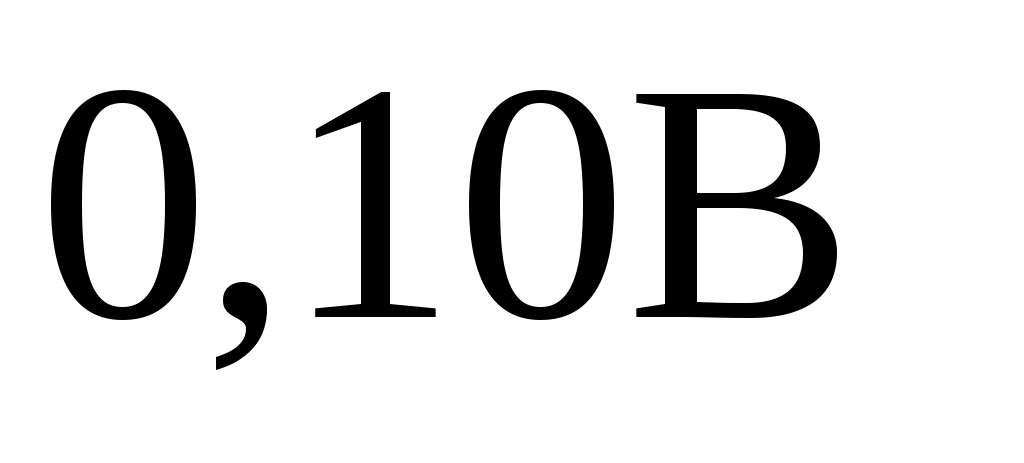 . Обозначение ячеек, полученных при таком разбиении, приведены во второй колонке табл. 5.
. Обозначение ячеек, полученных при таком разбиении, приведены во второй колонке табл. 5.
Число оцифрованных делений на каждой оси должно быть минимально необходимым для ясного понимания шкалы и составляет обычно от 4 до 10. По оси x цифры пишутся под масштабными рисками, обозначение откладываемой величины и ее единица измерения указываются справа под осью. По оси y цифры пишутся слева от рисок, а обозначение соответствующей величины и единица измерения указываются вверху слева от оси. Стрелки на осях не ставятся. Порядковый множитель 10m следует включать в буквенное обозначение или использовать десятичные приставки к названиям единиц. Например, «I, мкА», «R, кОм», «t, 10–2 , с».
Ни в коем случае не следует отмечать и оцифровывать на осях экспериментальные значения аргумента и функции, а тем более проводить штриховые линии для помещения экспериментальных точек на поле графика. Изобилие линий резко ухудшает восприятие графической информации. Следует помнить, что на графике, прежде всего, должны выделяться экспериментальные точки – именно они являются главным результатом работы экспериментатора.
Нанесение экспериментальных точек и их погрешностей. Экспериментальные точки нужно наносить на график точно и аккуратно, отмечая их кружками (квадратами, треугольниками, крестиками). Полезно применять разные знаки для разных кривых, если они изображаются на одном графике. Погрешности на графиках, когда это позволяет масштаб, можно указывать для одной или обеих измеряемых величин в виде отрезков, полудлина которых равна доверительной погрешности. Исключение составляют случаи, когда по одной из осей откладываются величины, известные точно (например, принимающие только целочисленные значения).
Обычно указание погрешностей либо загромождает график, либо их нельзя указать в данном масштабе (при точных измерениях). Поэтому допустимо иногда вообще не указывать погрешности или делать это для одной-двух точек. О точности измерений тогда можно весьма приближенно судить по разбросу точек относительно проведенной кривой.
Проведение кривой по экспериментальным точкам.
Экспериментальные точки соединяются карандашом плавной кривой так, чтобы они располагались примерно поровну и в среднем на равном удалении по обе стороны от кривой. Ни в коем случае не следует соединять экспериментальные точки на графике ломаной линией (от точки к точке). Обычно зависимости физических величин соответствуют гладким, плавно изменяющимся функциям без резких изломов и перегибов. Если же все точки последовательно соединить, то получится ломаная линия, которая не имеет ничего общего с истинной физической зависимостью. Это следует хотя бы из того факта, что форма полученной ломаной линии не будет воспроизводиться при повторных сериях измерений.
Проводимая на графике кривая не должна заслонять экспериментальные точки. Следует помнить, что именно точки являются результатом измерений, а кривая – лишь наше (не обязательно верное) толкование результата.
Оформление графиков. Графики должны быть снабжены заголовками и пояснениями, кратко и точно отражающими содержание графика. Обязательно указываются откладываемые по осям величины и их размерности. Если на одном графике располагается несколько кривых, то каждая из них должна быть четко обозначена цифрой или буквой, поясняемой в подписи к графику. Заголовок и пояснения располагают под графиком.
Лабораторная работа № 100
Измерение электронным секундомером интервалов времени,
задаваемых по механическому секундомеру
Цель работы – освоение алгоритма обработки результатов прямых многократных измерений, построение гистограммы экспериментальных значений определяемой величины и оценка параметров распределения Гаусса по кривой закона распределения.
Теоретическая часть
1. Измерение физических величин и графическое представление результатов измерений
При измерении физических величин в лабораторном практикуме из систематических погрешностей во внимание принимаются, как правило, только приборные как легко учитываемые. В таком случае в погрешность
определяемой величины входят две составляющие: случайная (статистическая)
Если приборная погрешность значительно больше случайной, то при многократных измерениях практически получается один и тот же результат. Этот недостаток присущ в основном стрелочным приборам, подвижная часть которых, связанная со стрелкой, бывает настолько инерционной, что либо не реагирует на малые случайные отклонения, либо эти отклонения настолько малы, что их практически невозможно регистрировать. Такой прибор принято называть грубым. Точный прибор характеризуется меньшей систематической (приборной) погрешностью по сравнению со случайной, и поэтому на распределении полученных с его помощью результатов измерений сказывается случайный разброс. Точными приборами являются цифровые вольтметры, электронные секундомеры и весы, измерители сопротивлений, емкостей и индуктивностей и т. д. Полученные с их помощью n значений одной и той же измеряемой физической величины при неизменных контролируемых условиях следует обрабатывать как результаты прямых многократных измерений.
Если измерения выполняют с помощью грубого и точного приборов, то необходимо исключить просчеты (промахи), связанные с отсутствием навыков измерения. Особое значение это имеет для уменьшения различия в показаниях механического и электронного секундомеров, обусловленного реакцией исследователя и проявляющегося в недновременности как включения, так и выключения счетного устройства. После нескольких измерений промежутков времени (длительностью, например, 60 секунд) с помощью электронного секундомера удается их фиксировать с погрешностью в несколько сотых секунды. Просчетов на механическом секундомере в силу его большей приборной погрешности избежать значительно легче.
Перед проведением статистического анализа целесообразно проверить, не изменяются ли измеренные значения регулярным образом со временем. Такое изменение называется дрейфом. Для выяснения этого вопроса необходимо построить график зависимости результатов наблюдений от времени. Часто время заменяют последовательностью порядковых номеров
i отдельных наблюдений, которые наносят на горизонтальную ось. По вертикальной оси наносят значения измеряемой величины (рис. 2).
На рис. 2, а дрейф отсутствует, на рис.2. б результаты систематически увеличиваются с течением времени (с увеличением порядкового номера наблюдения i).
При наличии дрейфа следует установить, связан ли он с неисправностью прибора (в этом случае устранить ее или заменить прибор) или с закономерным изменением определяемой величины (здесь необходимо специальное исследование). При отсутствии дрейфа нужно построить экспериментальную гистограмму, показывающую, как часто получаются те или иные значения
а)

б)

Рис. 2. Зависимость значений результатов измерения
от порядкового номера отсчета (от времени):
а – дрейф отсутствует; б – дрейф наблюдается;
точки – экспериментальные значения, прямые – аппроксимация точек
2. Пример построения гистограммы экспериментальных значений определяемой величины x и оценки параметров σ и x0 из кривой закона распределения
Пусть проведено 50 отсчетов величины напряжения, из которых
Учтем неравномерность распределения результатов наблюдений по всему диапазону. Это уменьшает число ячеек примерно в 1,5–2 раза. Возьмем 6 ячеек. Длина ячеек будет равна примерно