Файл: Федеральное агентство железнодорожного транспорта Федеральное государственное бюджетное.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 67
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
P = 1.
При P < 1 доверительная приборная погрешность рассчитывается по формуле
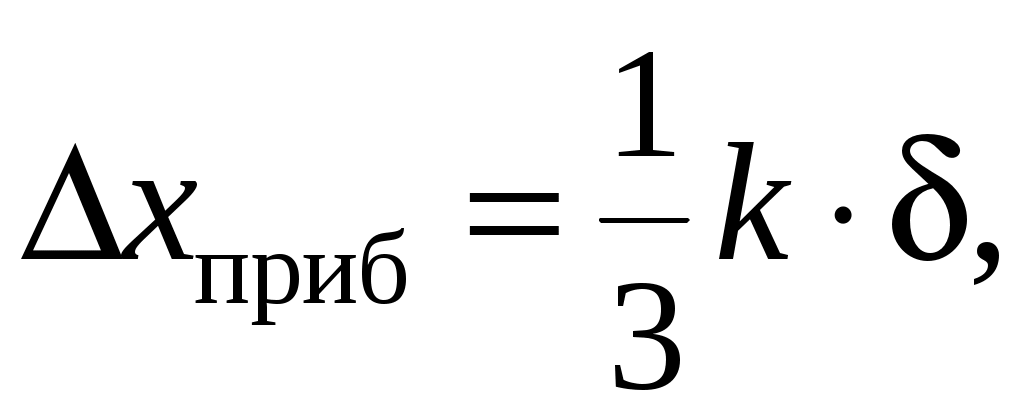 (9)
(9)
где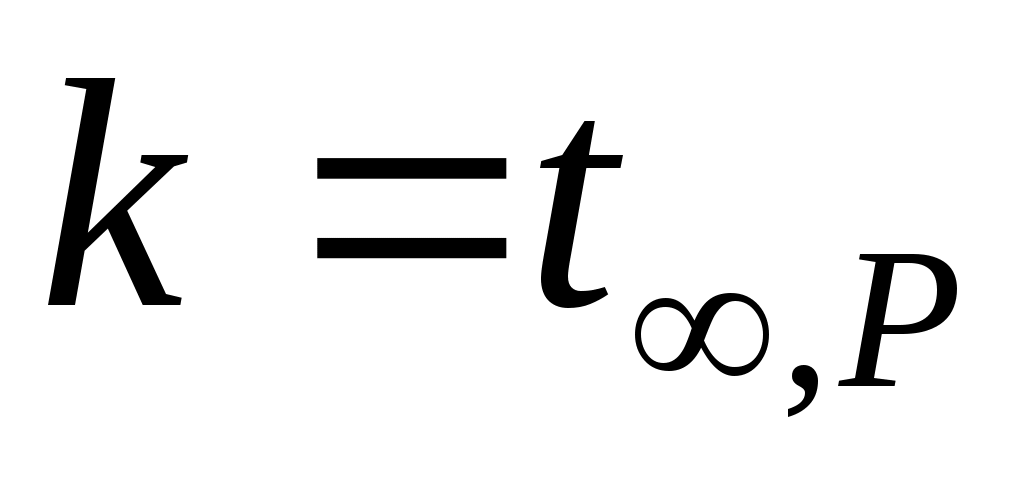 (при
(при 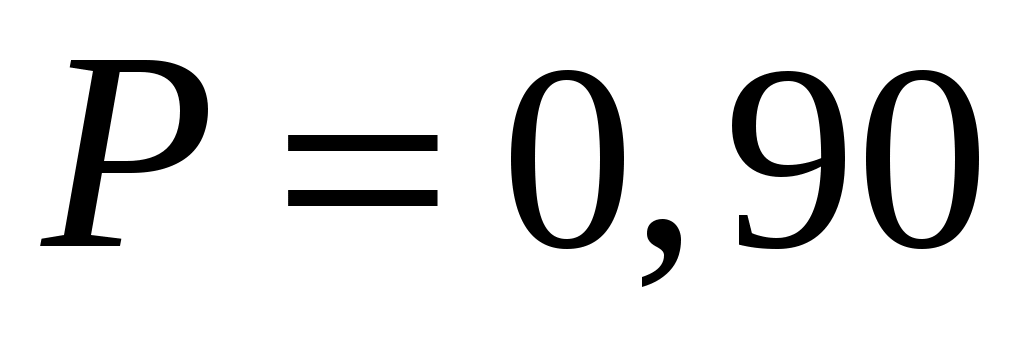
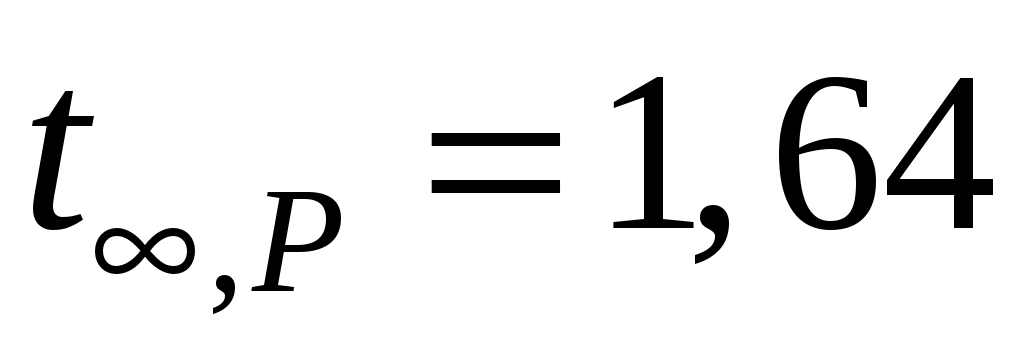 ), а значение предельной погрешности
), а значение предельной погрешности  определяется либо по классу точности по формуле (8), либо берется равным цене деления или половине цены деления прибора (см. табл. 4).
определяется либо по классу точности по формуле (8), либо берется равным цене деления или половине цены деления прибора (см. табл. 4).
Таблица 4
Предельные погрешности лабораторных приборов и инструментов
Обобщая правила вычисления погрешностей при прямых измерениях, необходимо иметь в виду следующее. В случае приблизительного равенства погрешностей
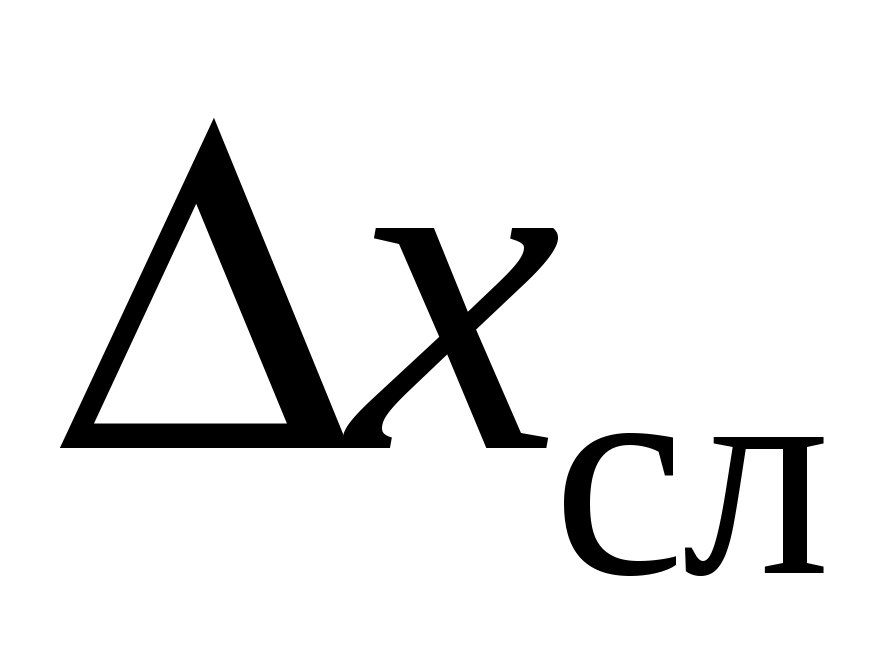 и
и 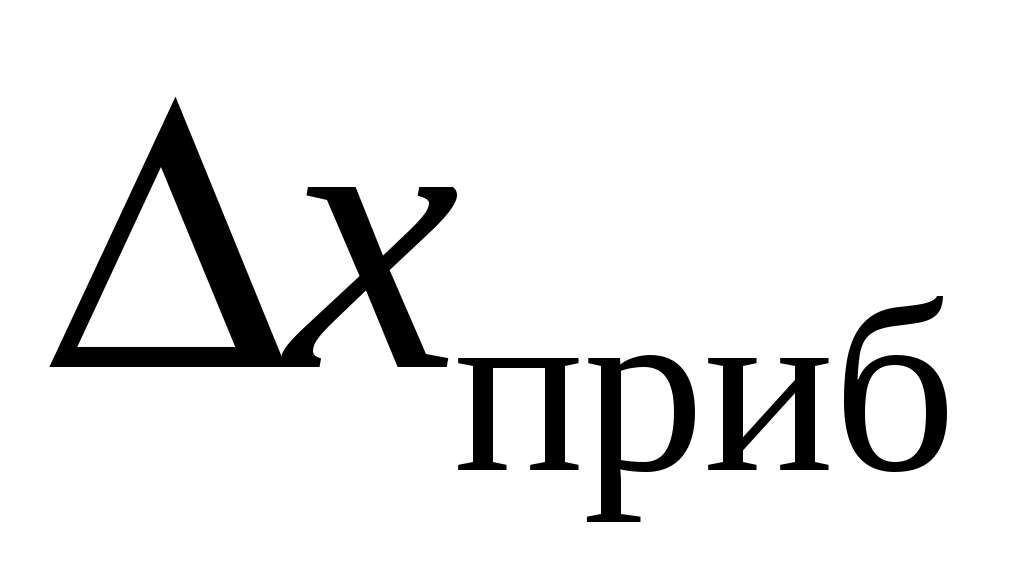 результирующую погрешность результата измерений вычисляют по формуле
результирующую погрешность результата измерений вычисляют по формуле
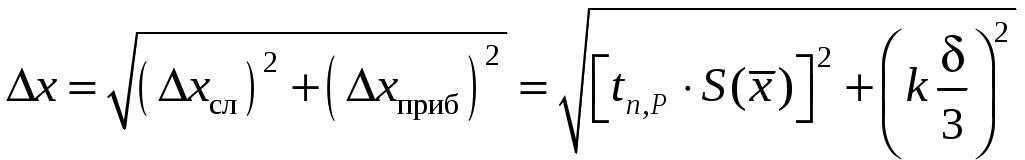 . (10)
. (10)
Если вычисленная по формуле (7) случайная погрешность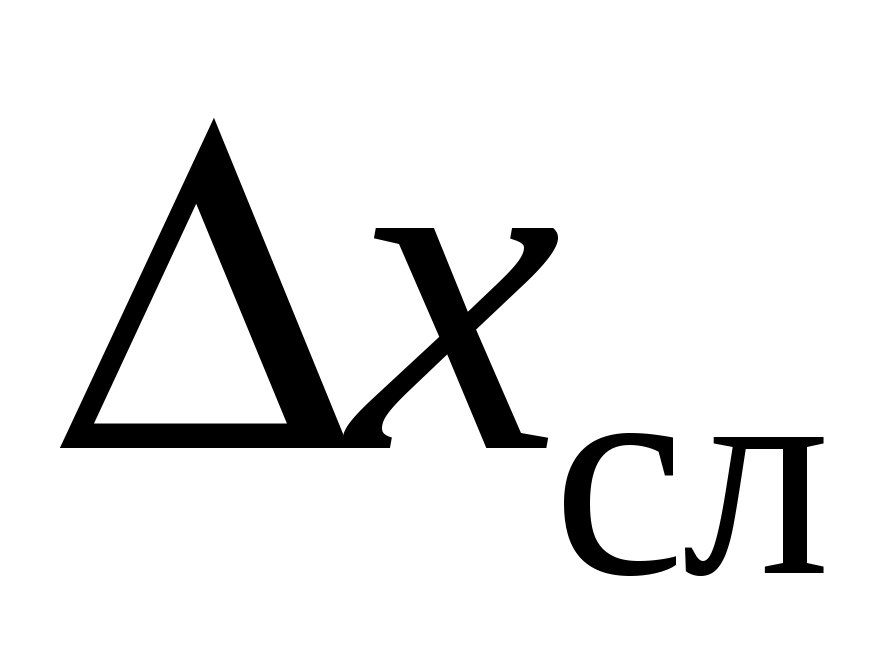 окажется по крайней мере в два раза меньше приборной
окажется по крайней мере в два раза меньше приборной 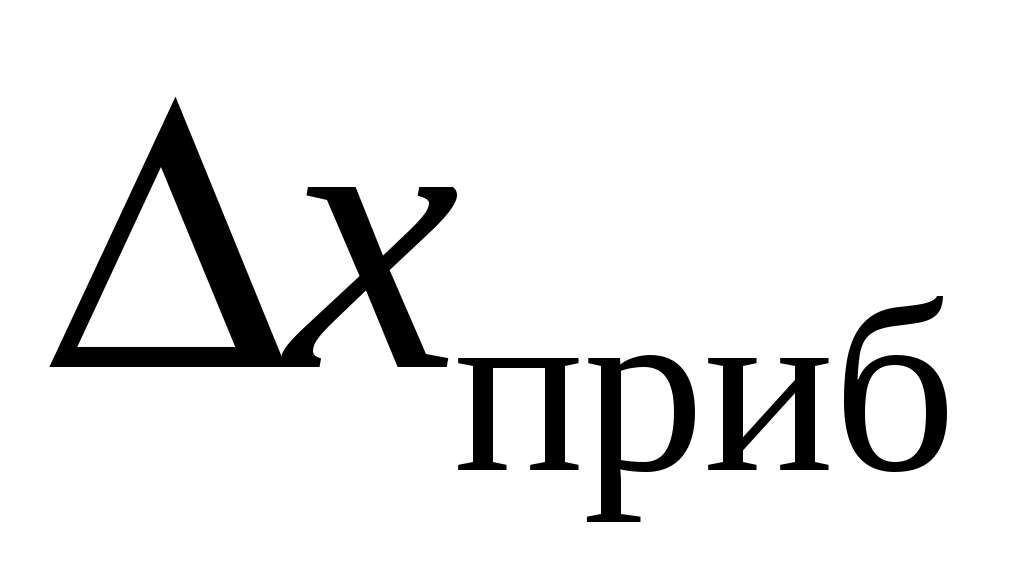 , то случайной погрешностью можно пренебречь, и тогда
, то случайной погрешностью можно пренебречь, и тогда 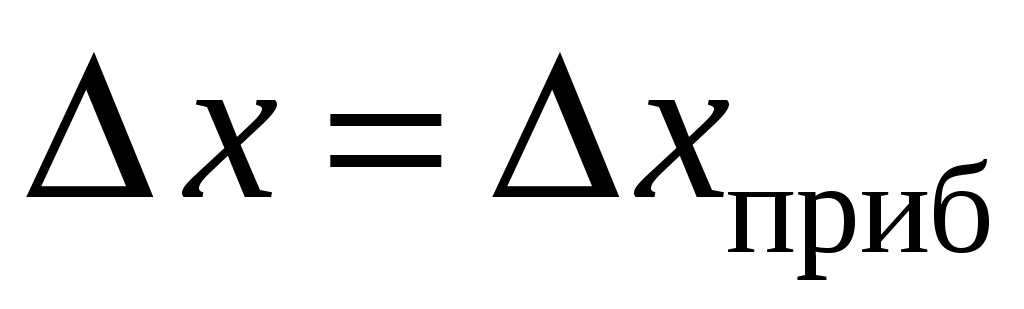 . И наоборот, когда случайная погрешность по крайней мере в два раза больше, чем приборная, то пренебрегают последней и
. И наоборот, когда случайная погрешность по крайней мере в два раза больше, чем приборная, то пренебрегают последней и 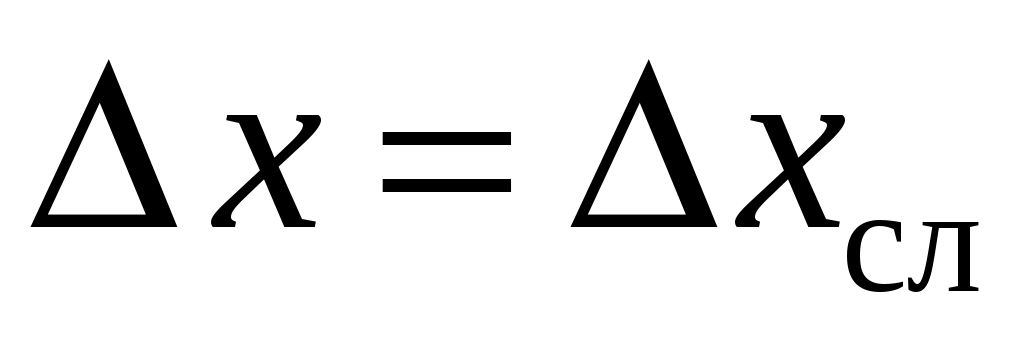 . Отметим, что случайную погрешность можно сделать очень малой величиной (например, за счет увеличения числа измерений), однако измерения не могут быть точнее, чем это допускает прибор.
. Отметим, что случайную погрешность можно сделать очень малой величиной (например, за счет увеличения числа измерений), однако измерения не могут быть точнее, чем это допускает прибор.
ВЫЧИСЛЕНИЕ ПОГРЕШНОСТЕЙ ПРИ КОСВЕННЫХ ИЗМЕРЕНИЯХ
В большинстве экспериментов интересующая нас величина непосредственно не измеряется. Вместо этого измеряются другие величины (аргументы)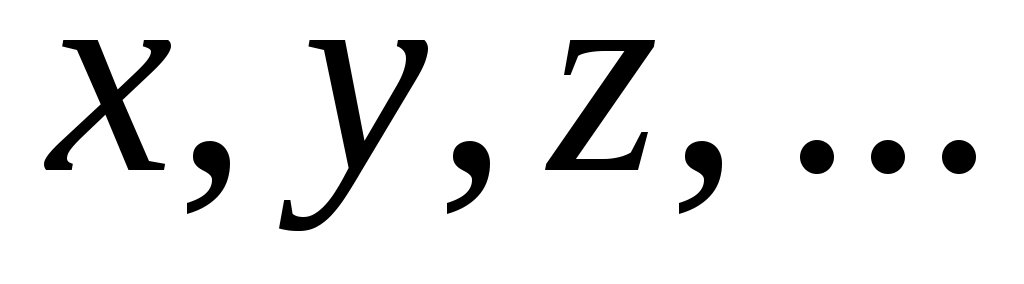 и т. д., а затем искомая величина A вычисляется на основе заданной функциональной зависимости
и т. д., а затем искомая величина A вычисляется на основе заданной функциональной зависимости
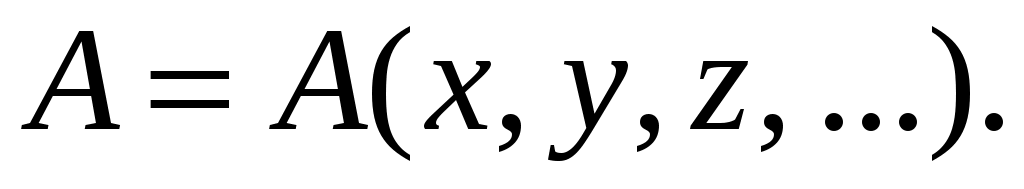 (11)
(11)
Если для каждого аргумента в выражении (11) экспериментально найдены средние значения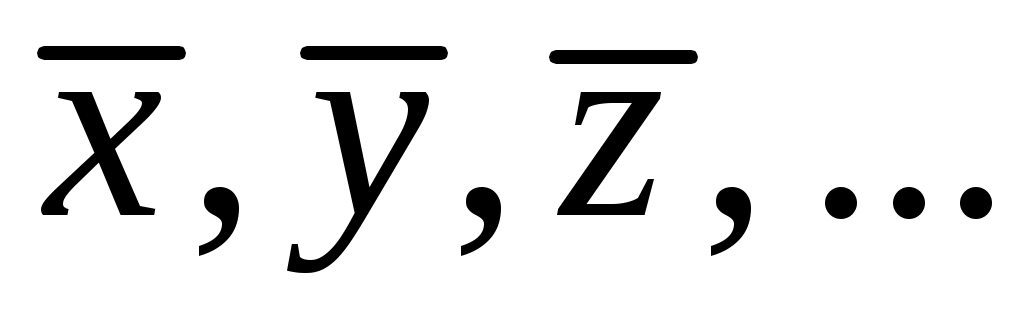 и вычислены погрешности
и вычислены погрешности 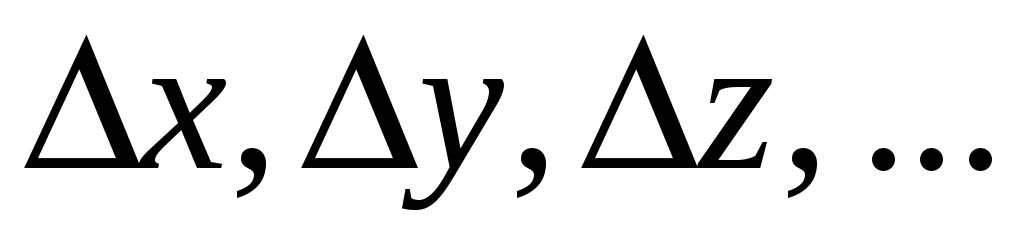 , то за наилучшее приближение для величины A принимается значение
, то за наилучшее приближение для величины A принимается значение
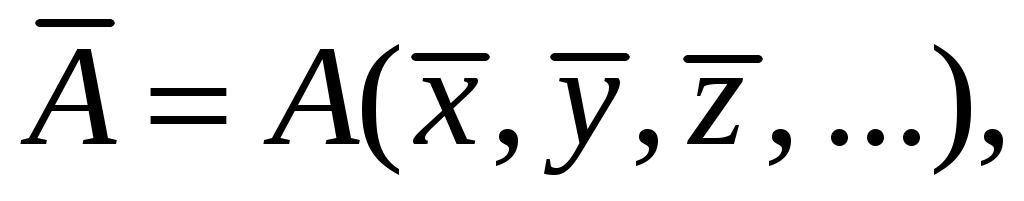
получающееся при подстановке в выражение (11) вместо истинных значений аргументов их средних экспериментальных значений.
Доверительная погрешность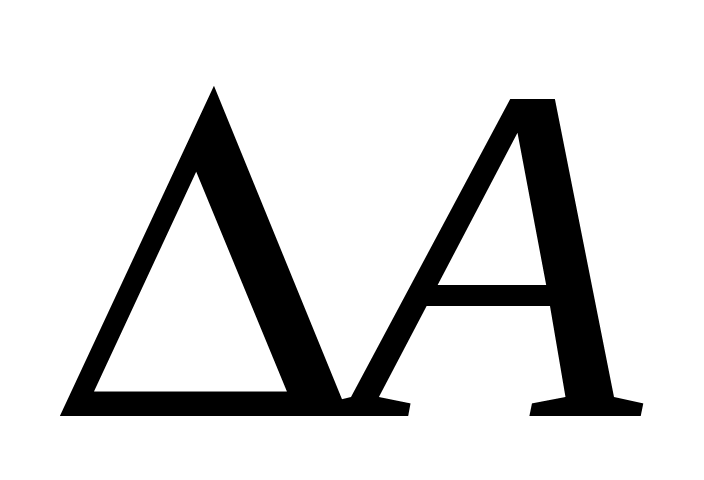 косвенных измерений величины
косвенных измерений величины
A определяется погрешностями прямых измерений (однократных или многократных) всех аргументов
прямых измерений (однократных или многократных) всех аргументов 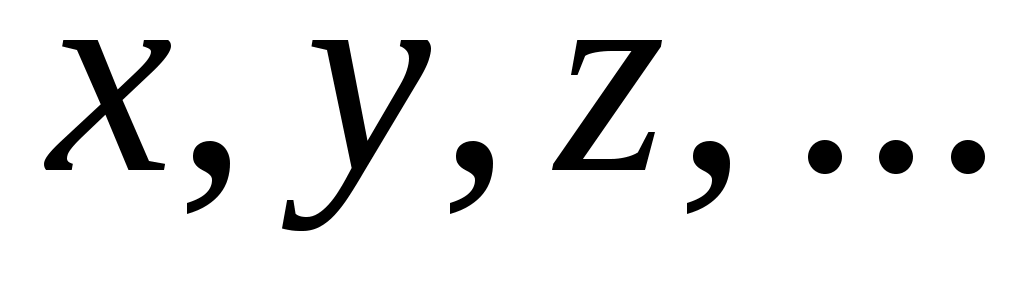 , входящих в формулу (11).
, входящих в формулу (11).
Полное приращение функции
функции 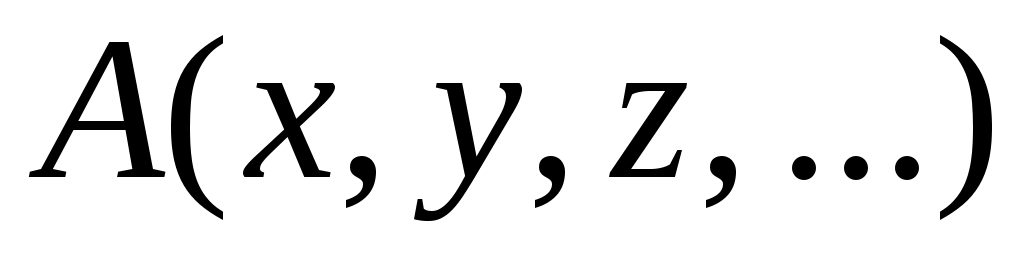 , обусловленное изменением ее аргументов на малые величины
, обусловленное изменением ее аргументов на малые величины  , может быть, как известно из курса высшей математики, c достаточной точностью вычислено по формуле
, может быть, как известно из курса высшей математики, c достаточной точностью вычислено по формуле
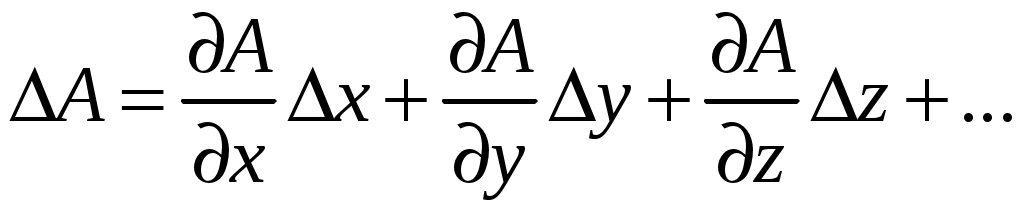 , (12)
, (12)
где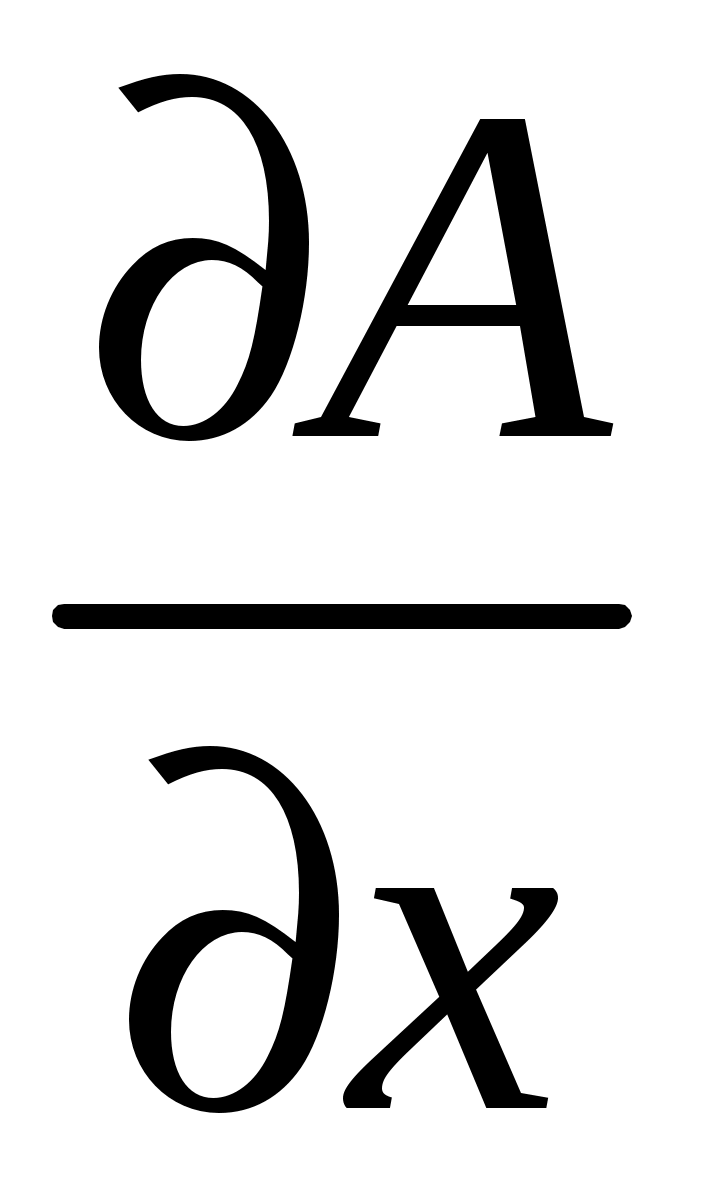 ,
, 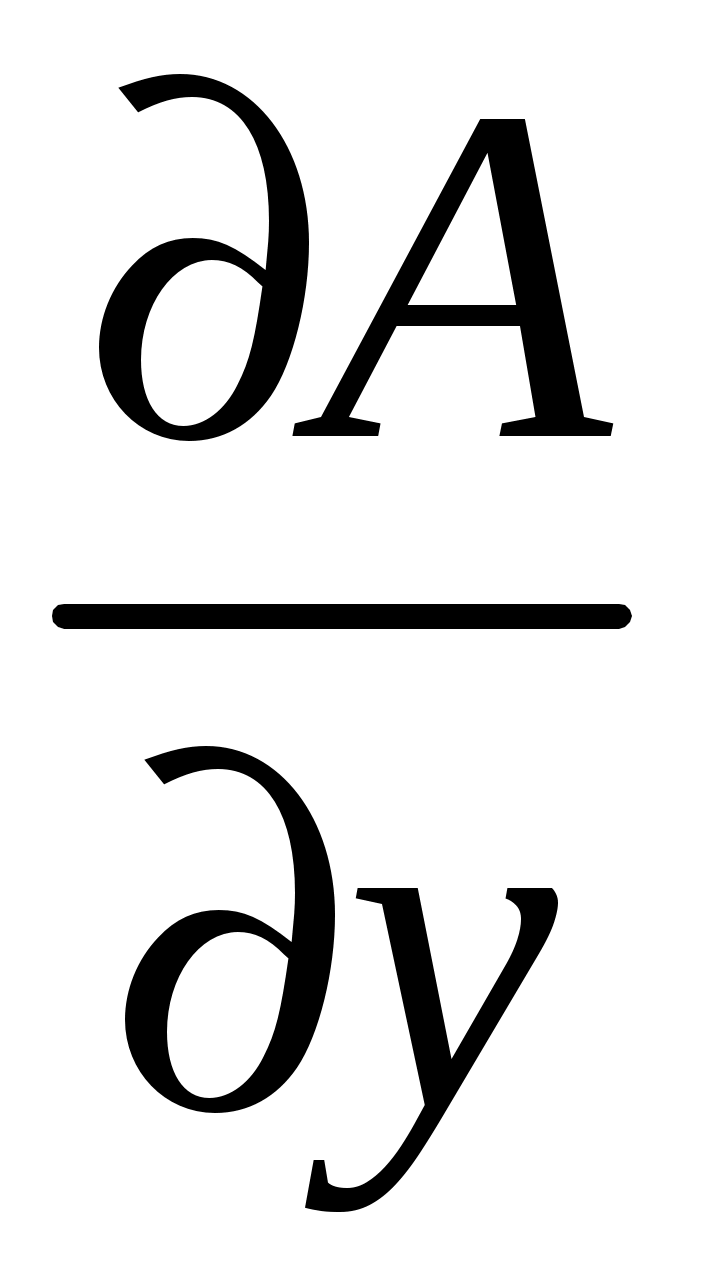 ,
, 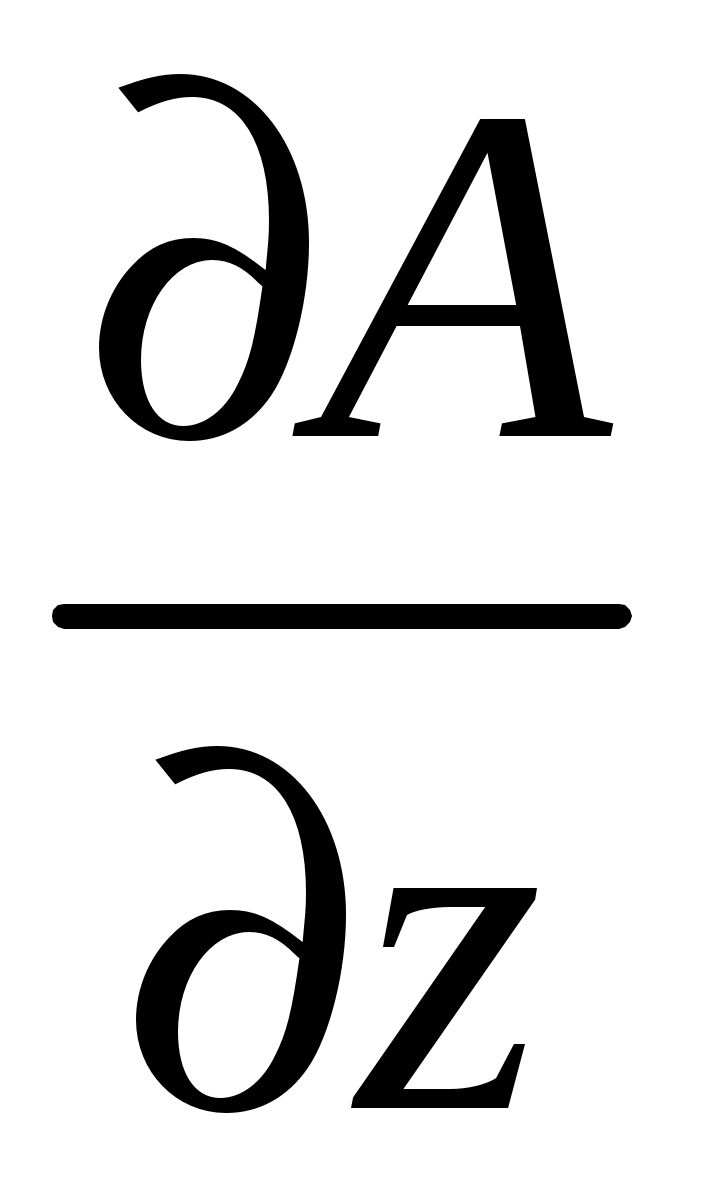 – частные производные функции A по ее соответствующим аргументам.
– частные производные функции A по ее соответствующим аргументам.
Напомним, что при вычислении частной производной все аргументы функции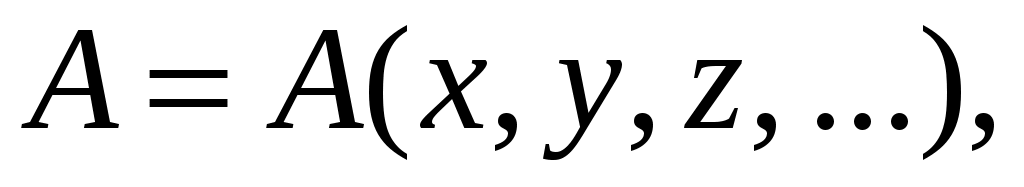 кроме того, по которому производится дифференцирование, считаются постоянными.
кроме того, по которому производится дифференцирование, считаются постоянными.
Рассматривая в выражении (12) величины как погрешности прямых (однократных или многократных) измерений аргументов, можем считать каждое из слагаемых правой части этой формулы вкладом в общую погрешность измерений функции A. Полагая эти вклады независимыми, по доказанному в математической статистике закону сложения погрешностей получаем общую формулу для вычисления погрешности
как погрешности прямых (однократных или многократных) измерений аргументов, можем считать каждое из слагаемых правой части этой формулы вкладом в общую погрешность измерений функции A. Полагая эти вклады независимыми, по доказанному в математической статистике закону сложения погрешностей получаем общую формулу для вычисления погрешности  при косвенных измерениях
при косвенных измерениях
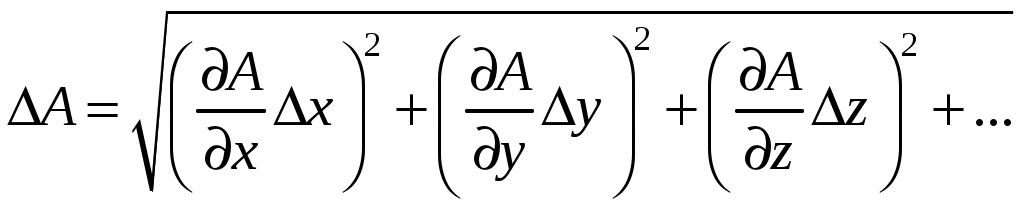 (13)
(13)
Таким образом, для того чтобы определить абсолютную погрешность результата косвенного измерения, следует найти частные производные функции A по всем аргументам, подставить в них найденные на предыдущем этапе измерений средние значения аргументов и произвести расчет по формуле (13).
и произвести расчет по формуле (13).
При расчете погрешностей по формуле (13) допустимо пренебрегать теми слагаемыми подкоренного выражения, которые по крайней мере в 2–3 раза меньше максимального (коэффициент 3 применяется в тех случаях, когда слагаемых много и малые погрешности могут внести заметный вклад в общую погрешность). Это соображение существенно упрощает расчет погрешности, а также позволяет четко выявить тот аргумент, погрешность которого имеет определяющее значение. Данный подход удобен при обсуждении результатов и важен для поиска путей повышения их точности.
Если искомая функция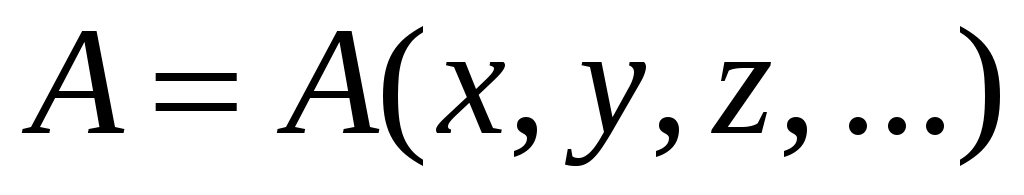 удобна для логарифмирования (состоит из множителей и делителей в разных степенях), учитывают, что полное приращение функции
удобна для логарифмирования (состоит из множителей и делителей в разных степенях), учитывают, что полное приращение функции 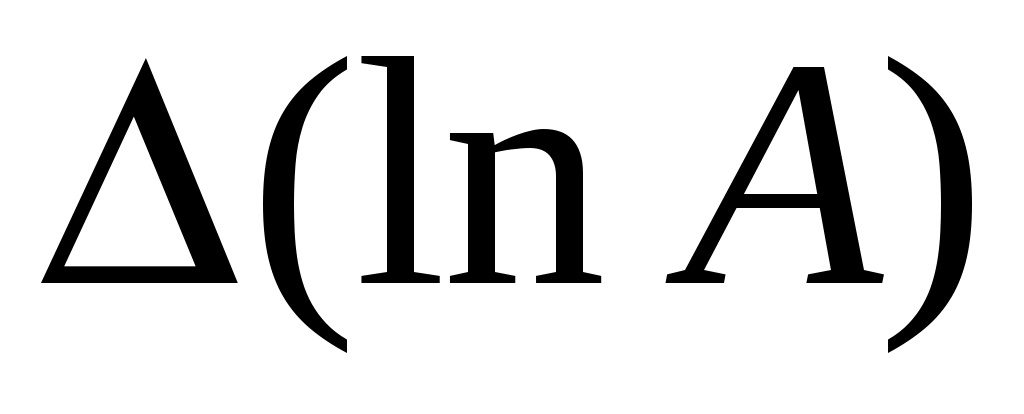 может быть с достаточной точностью рассчитано по формуле
может быть с достаточной точностью рассчитано по формуле
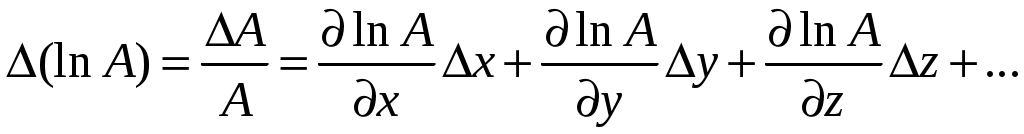 , (14)
, (14)
и вместо выражения (13) получают следующее соотношение:
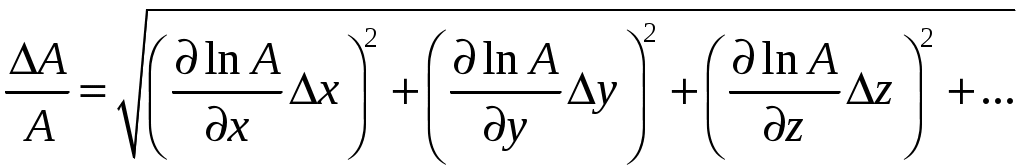 (15)
(15)
Заметим, что правая часть выражения (15) дает значение относительной погрешности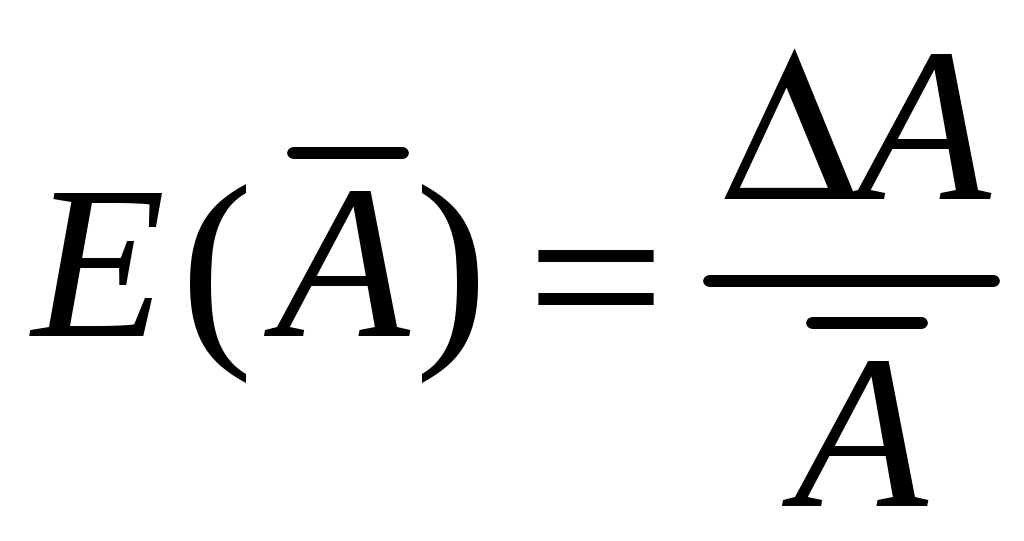 . Практика расчетов погрешностей результатов косвенных измерений свидетельствует о том, что вычислить относительную погрешность по формуле (15), а затем абсолютную погрешность из соотношения
. Практика расчетов погрешностей результатов косвенных измерений свидетельствует о том, что вычислить относительную погрешность по формуле (15), а затем абсолютную погрешность из соотношения 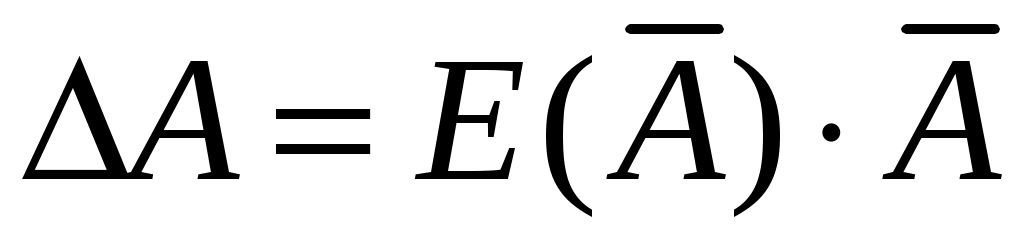 оказывается проще, чем производить расчеты по формуле (13).
оказывается проще, чем производить расчеты по формуле (13).
Окончательно рекомендуется следующий алгоритм обработки результатов косвенных измерений.
1. Выполнить (однократные или многократные) прямые измерения аргументов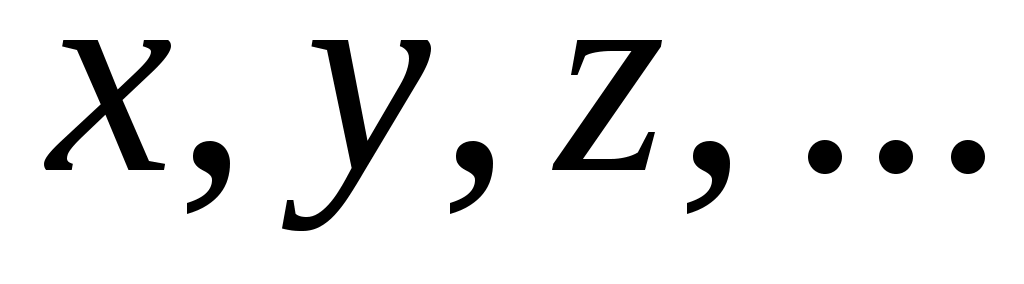 измеряемой функции
измеряемой функции 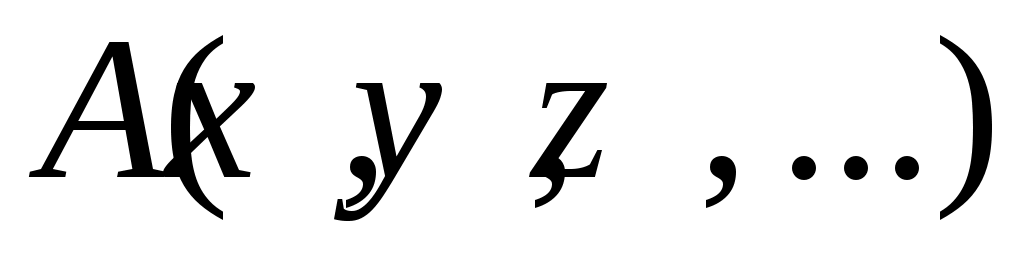 :
:
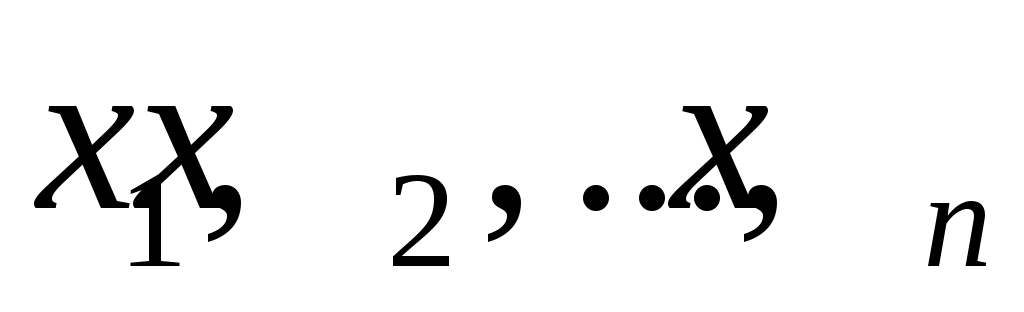 ;
; 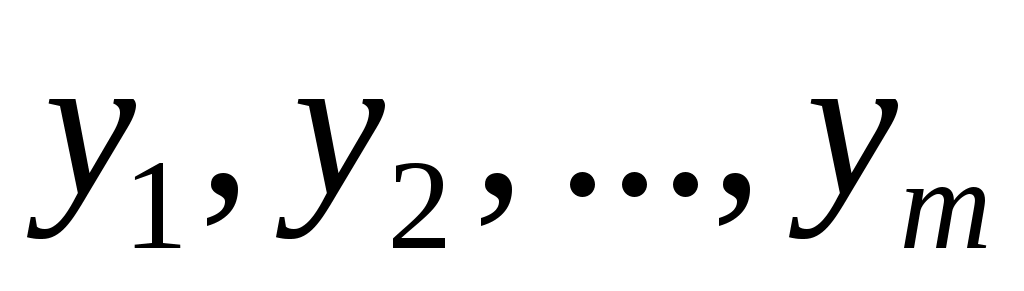 ;
; 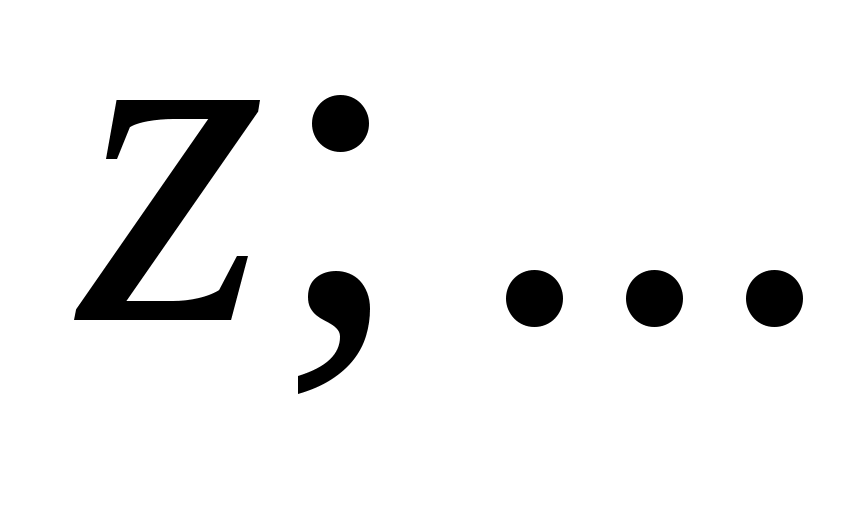
,
где n – число наблюдений аргумента x; m – число наблюдений аргумента y. (Подразумевается, что величина z является результатом однократного прямого измерения.)
2. Найти среднее арифметические значение аргументов
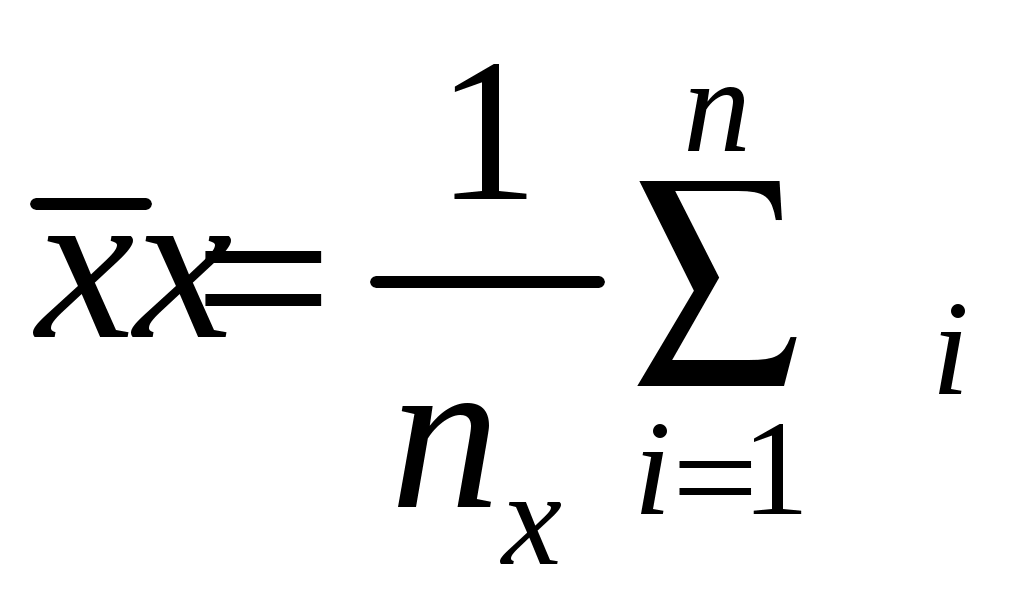 ;
; 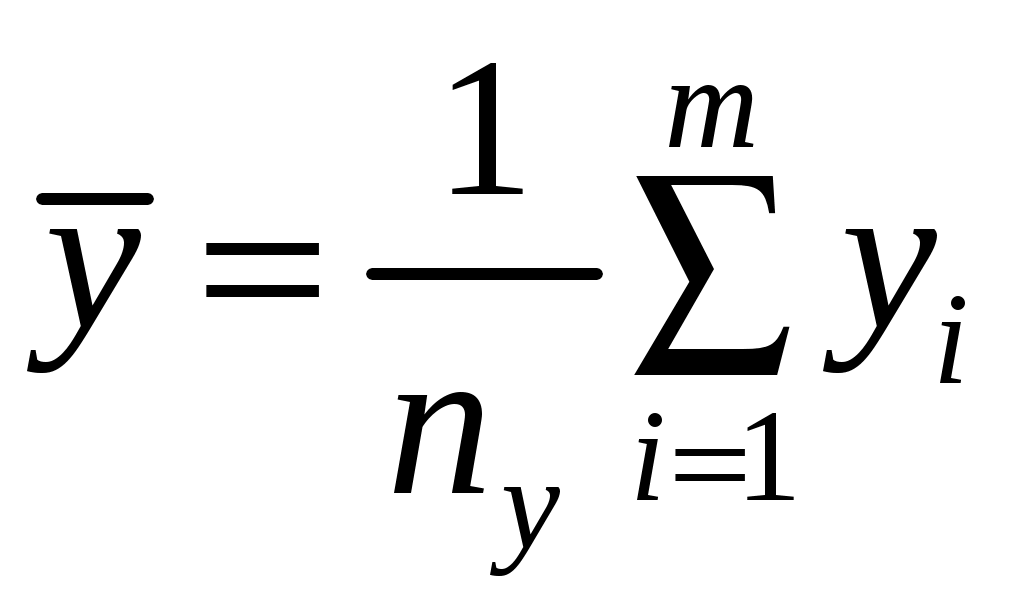 ;
; 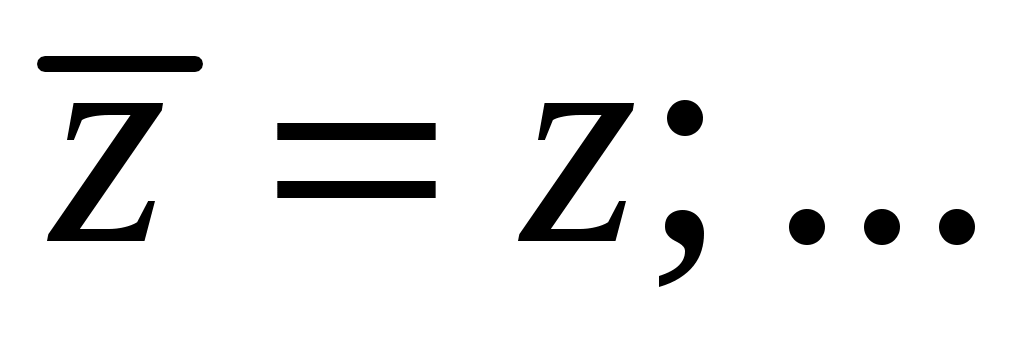
3. Вычислить предварительный результат измерений
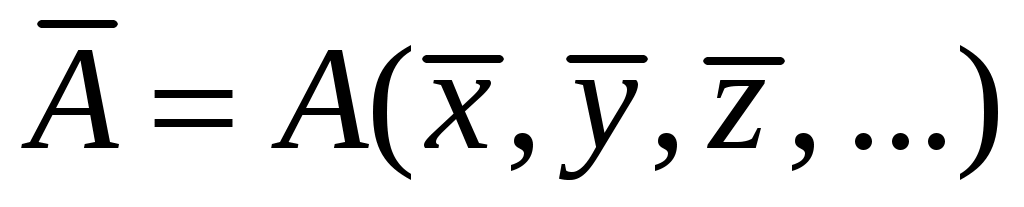 .
.
4. Вычислить абсолютные погрешности отдельных результатов наблюдений для каждого аргумента (при многократных его измерениях), а также их квадраты и соответствующие суммы:
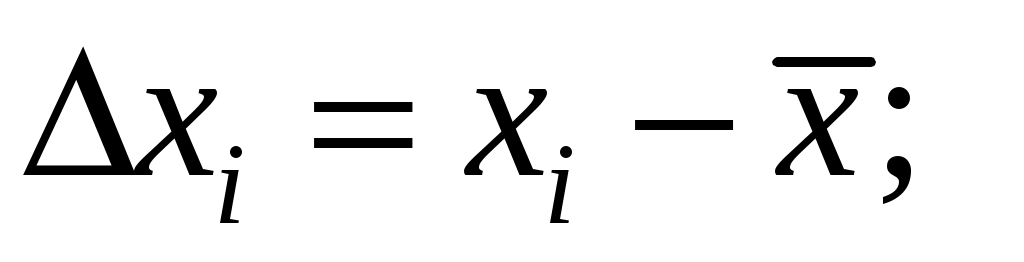
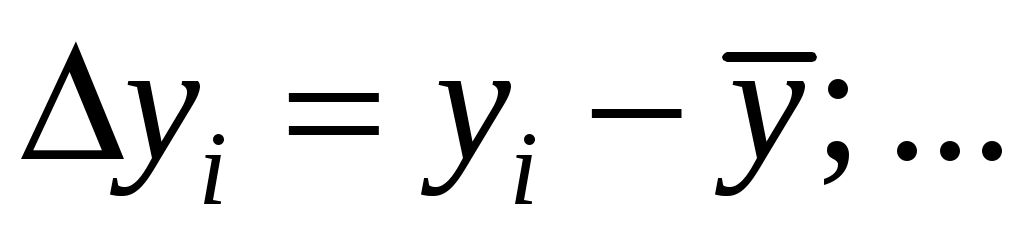
 ;
;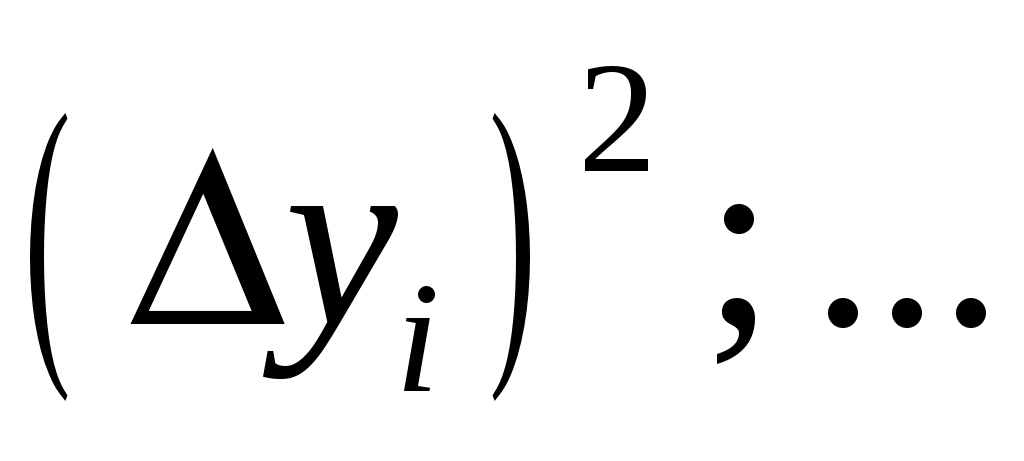
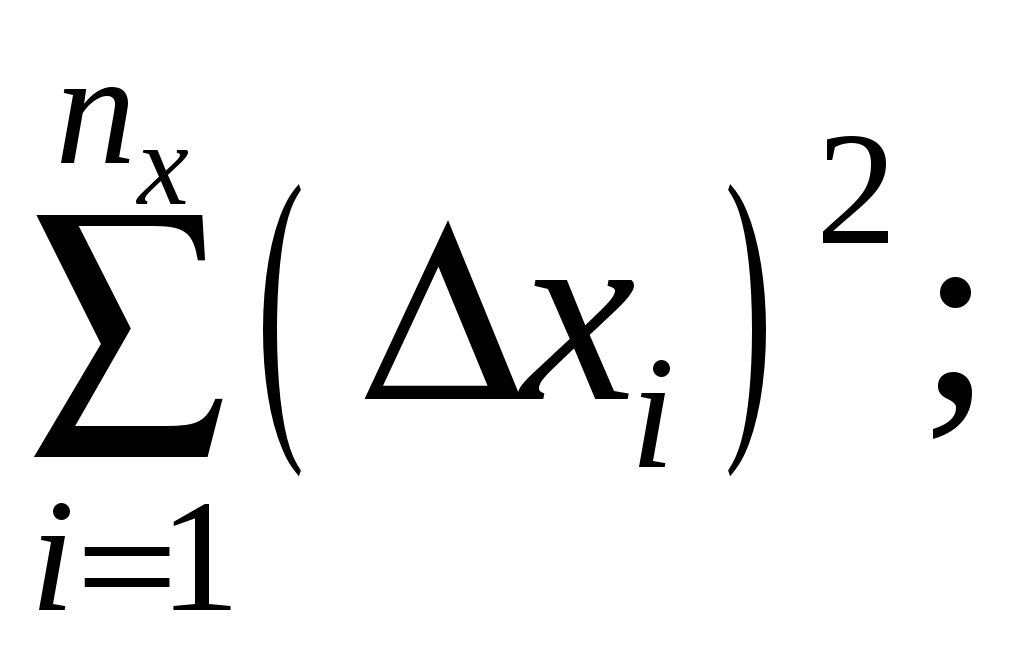
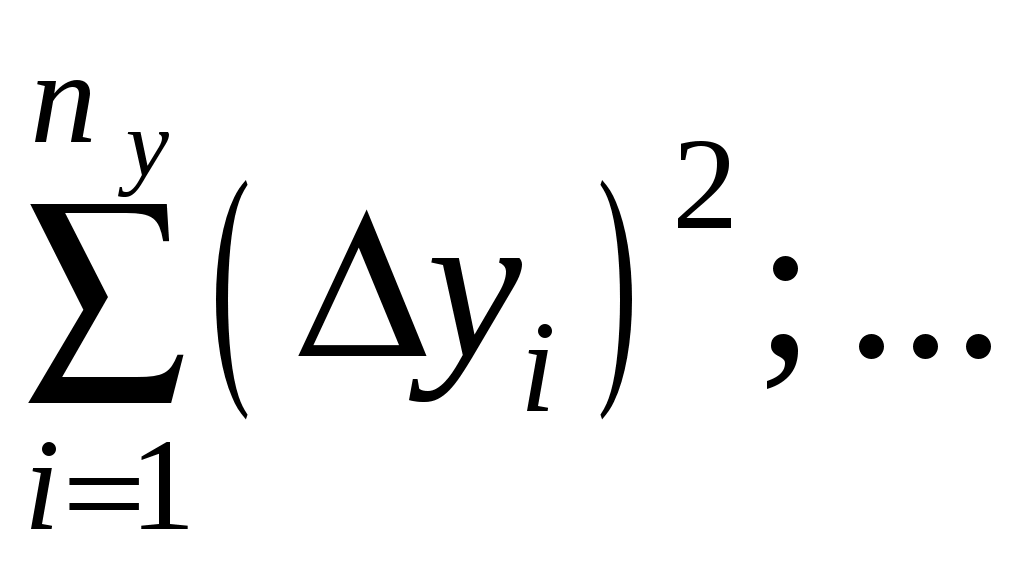
5. Для данных значений n, m и P найти по таблице коэффициент Стьюдента и вычислить погрешности аргументов (случайные или приборные):
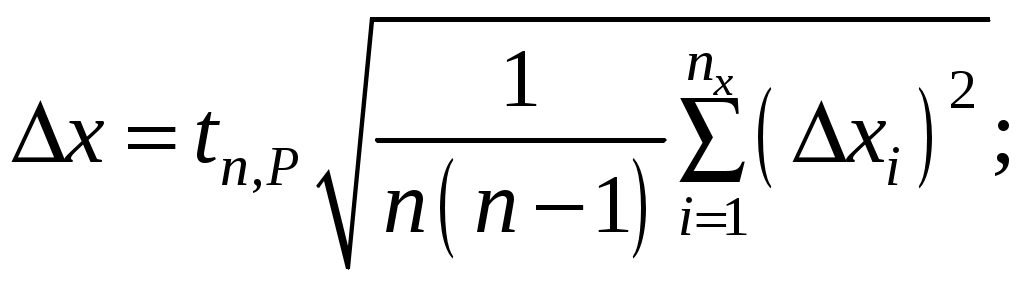
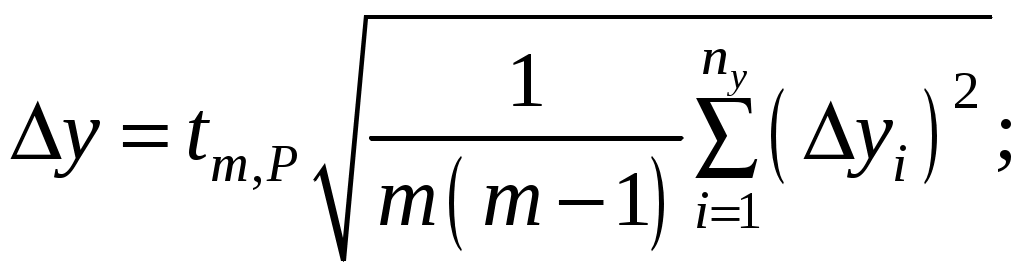
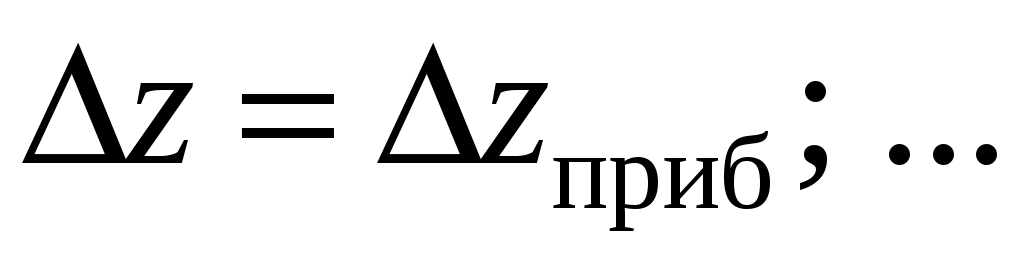
6. Если функция удобна для логарифмирования, прологарифмировать ее и по формуле (15) вычислить относительную погрешность:
удобна для логарифмирования, прологарифмировать ее и по формуле (15) вычислить относительную погрешность:
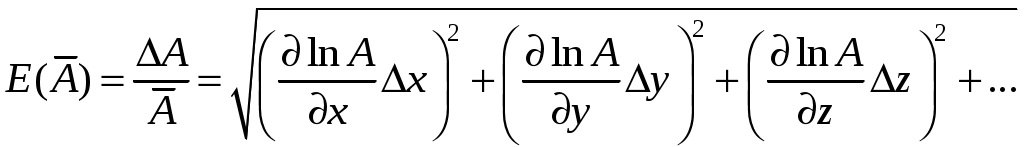 ,
,
а затем абсолютную погрешность .
.
Если функция неудобна для логарифмирования, то определить доверительную погрешность
При P < 1 доверительная приборная погрешность рассчитывается по формуле
где
Таблица 4
Предельные погрешности лабораторных приборов и инструментов
| Прибор или инструмент | Цена деления прибора | Предельная погрешность δ (Р = 1) |
| Измерительная линейка | 1 мм/дел | 1 мм |
| 1 см/дел | 0,5 см | |
| Штангенциркуль | 0,1 мм/дел | 0,1 мм |
| 0,05 мм/дел | 0,05 мм | |
| Микрометр | 0,01 мм/дел | 0,01 мм |
| Весы технические до 2 кг | | 1 г |
| Весы аналитические до 0,2 кг | 0,1 мг/дел | 0,1 мг |
| Секундомер электронный | 0,001 с/дел | 0,001 с |
| Часы с секундной стрелкой | 1 с/дел | 1 с |
| Прибор с указанным классом точности K | C | 10–2 · K · xmax |
| Электроизмерительный прибор без класса точности | C | C · 1 дел. |
| Магазины и мосты без класса точности K и без паспортных данных | C | ±5 % от измеренной величины |
| Табличная величина | | ±0,5 единицы последнего приведенного в ее записи разряда |
Обобщая правила вычисления погрешностей при прямых измерениях, необходимо иметь в виду следующее. В случае приблизительного равенства погрешностей
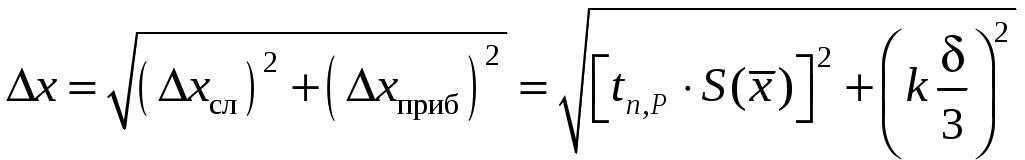 . (10)
. (10)Если вычисленная по формуле (7) случайная погрешность
ВЫЧИСЛЕНИЕ ПОГРЕШНОСТЕЙ ПРИ КОСВЕННЫХ ИЗМЕРЕНИЯХ
В большинстве экспериментов интересующая нас величина непосредственно не измеряется. Вместо этого измеряются другие величины (аргументы)
Если для каждого аргумента в выражении (11) экспериментально найдены средние значения
получающееся при подстановке в выражение (11) вместо истинных значений аргументов их средних экспериментальных значений.
Доверительная погрешность
A определяется погрешностями
Полное приращение
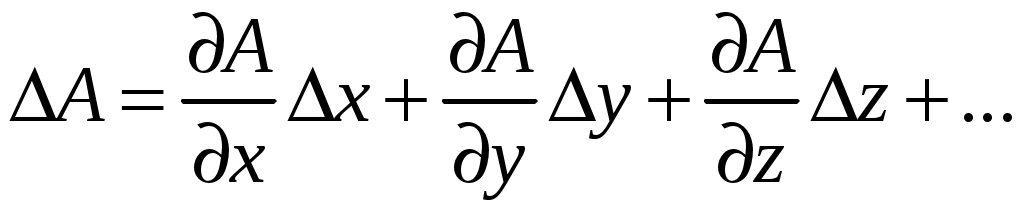 , (12)
, (12)где
Напомним, что при вычислении частной производной все аргументы функции
Рассматривая в выражении (12) величины
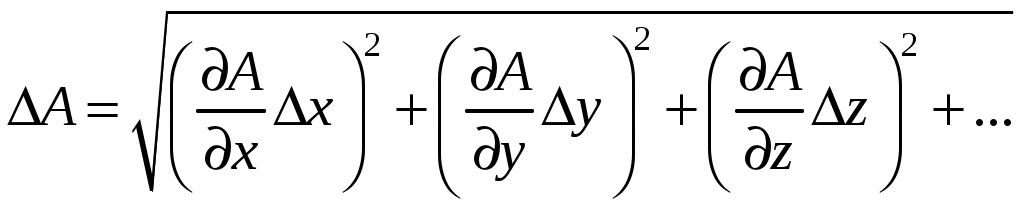 (13)
(13)Таким образом, для того чтобы определить абсолютную погрешность результата косвенного измерения, следует найти частные производные функции A по всем аргументам, подставить в них найденные на предыдущем этапе измерений средние значения аргументов
При расчете погрешностей по формуле (13) допустимо пренебрегать теми слагаемыми подкоренного выражения, которые по крайней мере в 2–3 раза меньше максимального (коэффициент 3 применяется в тех случаях, когда слагаемых много и малые погрешности могут внести заметный вклад в общую погрешность). Это соображение существенно упрощает расчет погрешности, а также позволяет четко выявить тот аргумент, погрешность которого имеет определяющее значение. Данный подход удобен при обсуждении результатов и важен для поиска путей повышения их точности.
Если искомая функция
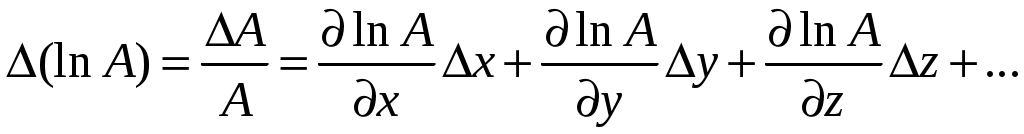 , (14)
, (14)и вместо выражения (13) получают следующее соотношение:
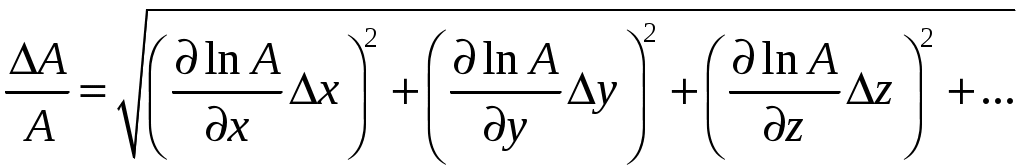 (15)
(15)Заметим, что правая часть выражения (15) дает значение относительной погрешности
Окончательно рекомендуется следующий алгоритм обработки результатов косвенных измерений.
1. Выполнить (однократные или многократные) прямые измерения аргументов
,
где n – число наблюдений аргумента x; m – число наблюдений аргумента y. (Подразумевается, что величина z является результатом однократного прямого измерения.)
2. Найти среднее арифметические значение аргументов
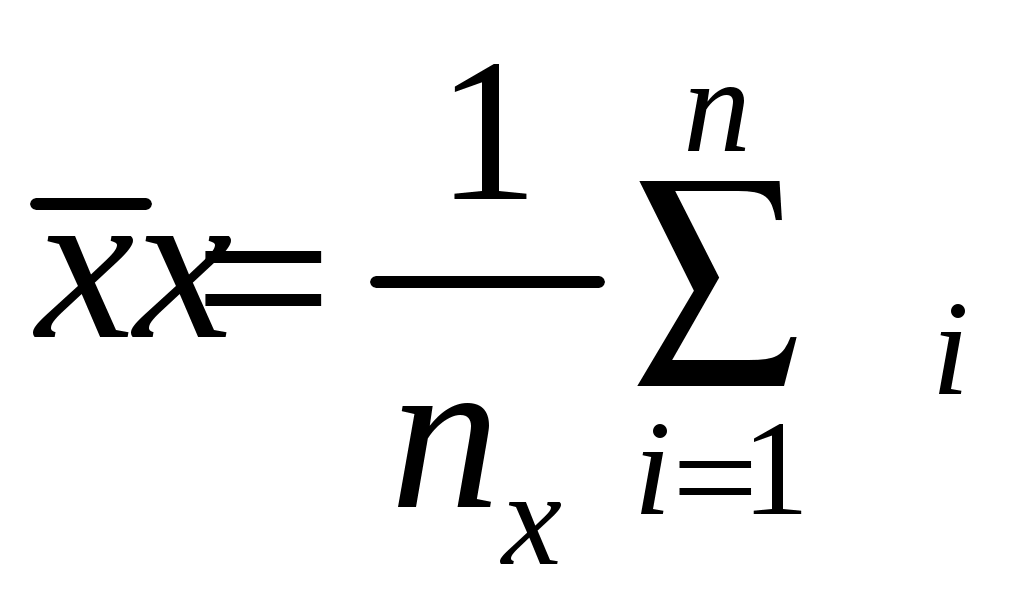 ;
; 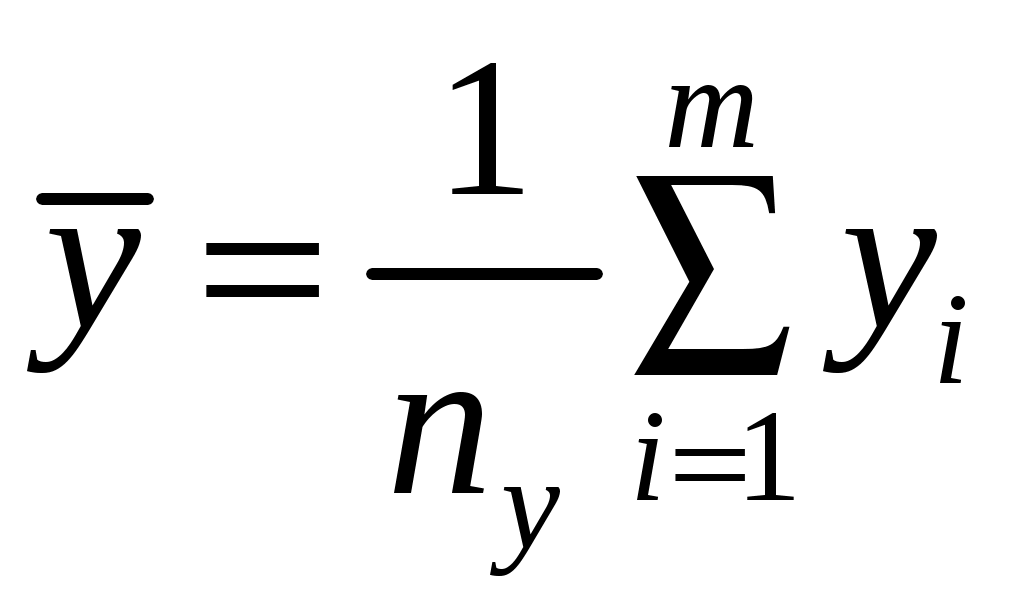 ;
; 3. Вычислить предварительный результат измерений
4. Вычислить абсолютные погрешности отдельных результатов наблюдений для каждого аргумента (при многократных его измерениях), а также их квадраты и соответствующие суммы:
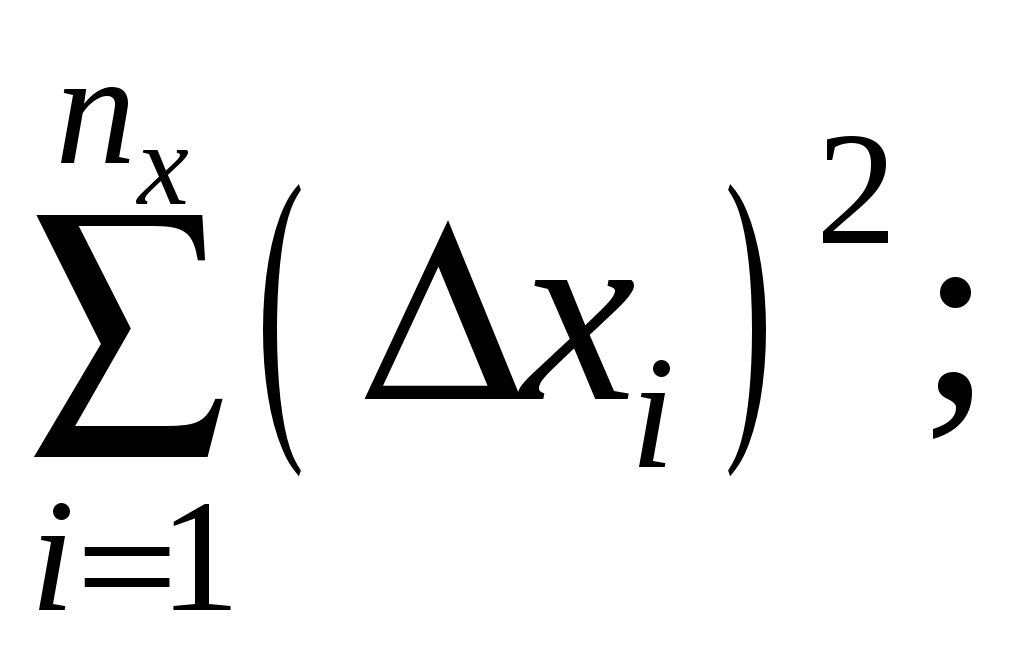
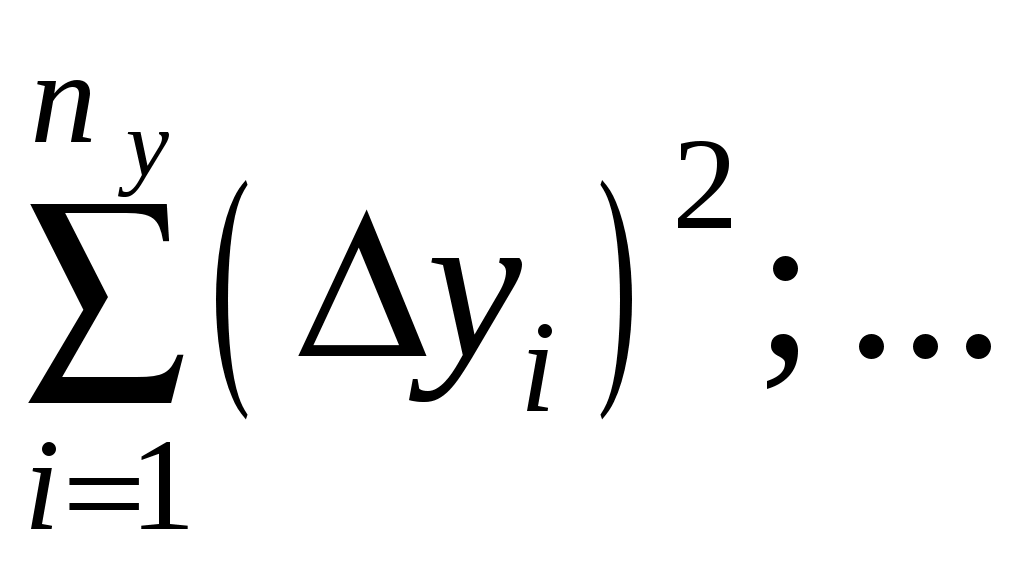
5. Для данных значений n, m и P найти по таблице коэффициент Стьюдента и вычислить погрешности аргументов (случайные или приборные):
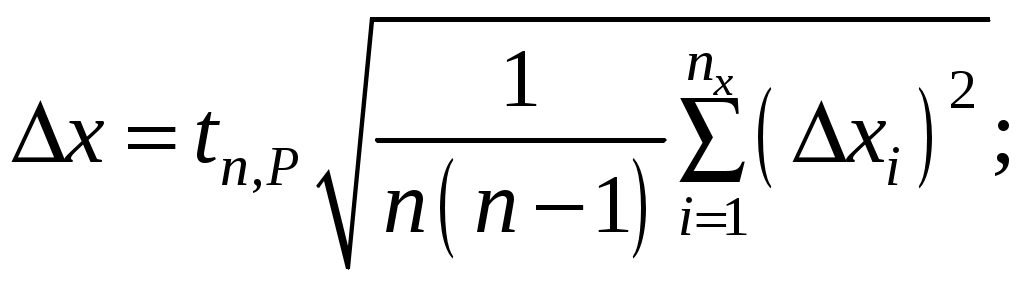
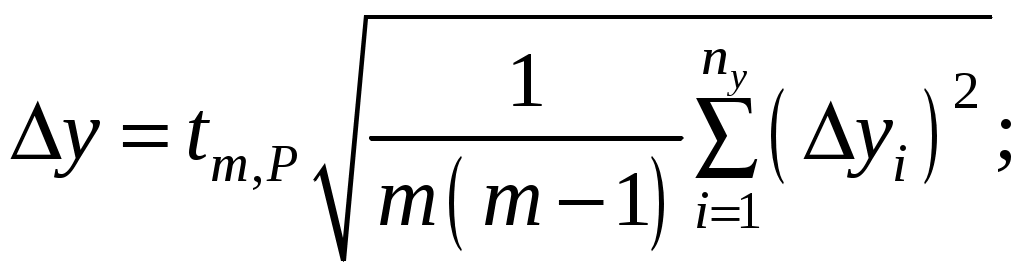
6. Если функция
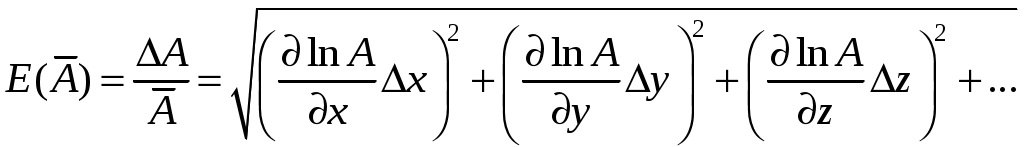 ,
,а затем абсолютную погрешность
Если функция неудобна для логарифмирования, то определить доверительную погрешность