Файл: Решение одноиндексных оптимизационных задач Цель работы научиться решать одноиндексные оптимизационные задачи производства.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 143
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
5. Следовательно, минимум целевой функции может быть получен только при нулевых значениях искусственных переменных.
Целевая функция нашей задачи примет следующее выражение:
F= 0,5x1 + 0,6x2 + 0,4x3 + 0,2x4 + 0,3x5-0x6-0x7-0x8 -0 x9+My1+ My2+ My3+ My4 = min
Теперь все готово для решения задачи. Можно приступить к составлению первой симплексной рис. (2.41), которая будет иметь точно такой же вид, как и в задачах, рассмотренных ранее.
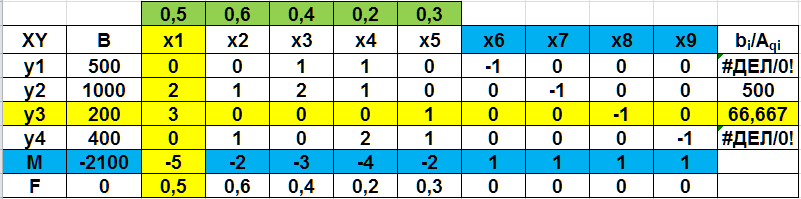
Рис. 2.41. Первая симплекс-таблица
В первоначальную программу войдут все искусственные переменные. Однако есть и некоторая особенность таблицы, заключающаяся в том, что в задачу входит неопределенное число М. Строка М формируется как отрицательная сумма предыдущих строк: столбец В -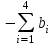
; столбцы х1–х9 - 
.
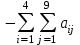Далее выбираем разрешающий столбец, но поскольку задача решается на минимум, в строке F выбираем положительные элементы, а строке М – максимальный по модулю отрицательный элемент (за исключением столбца В). Таким образом выбран столбец 1 (х1).
Далее, оцениваем отношения элементов столбца В к элементам разрешающего столбца (bi/Aqi), и выбираем большее положительное значение (строка 3 – y3). После этого по аналогичному алгоритму, рассмотренному ранее, пересчитываем вторую таблицу (рис. 2.42)
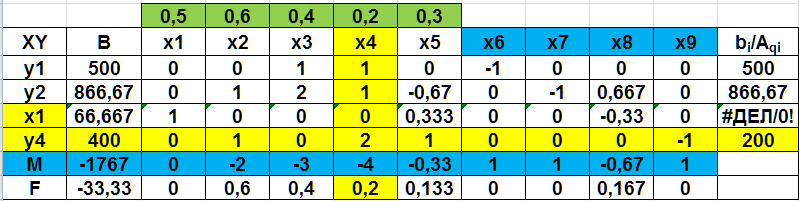
Рис. 2.42 Вторая симплекс-таблица
В этой таблице разрешающий столбец – 4 (х4), а разрешающая строка – 4 (y4). Переходим к расчету третьей и т.д. таблицам (рис. 2.43-2.45).
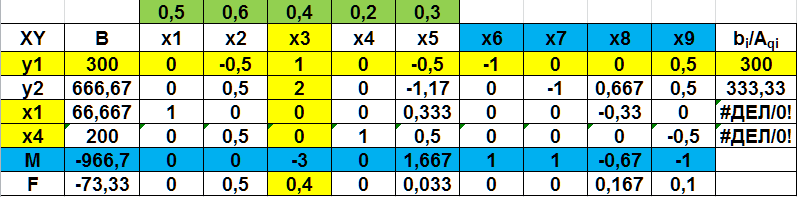
Рис. 2.43 Третья симплекс-таблица
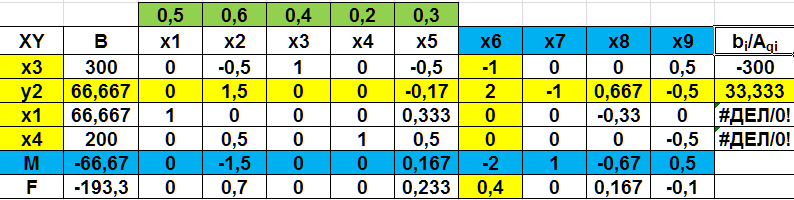
Рис. 2.44 Четвертая симплекс-таблица
На пятой итерации (рис. 2.45) получаем в строке М все нули, а все искусственные переменные y1- y4 замещены на основные и базисные переменные х.
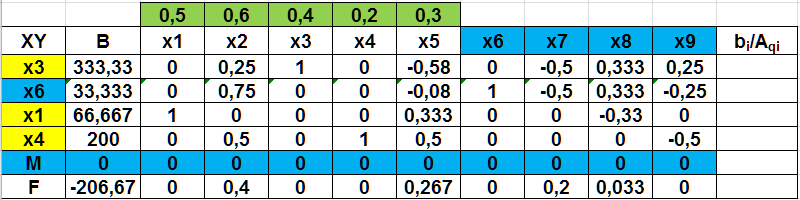
Рис. 2.45 Пятая симплекс-таблица
Следовательно, получаем оптимальное решение F-206,67=0, или F=206,67, при х1=66,667, х3=333,33, х4=200. Значение х6=33,33 показывает насколько первое ограничение превышает значение ресурса 500.
Целевая функция нашей задачи примет следующее выражение:
F= 0,5x1 + 0,6x2 + 0,4x3 + 0,2x4 + 0,3x5-0x6-0x7-0x8 -0 x9+My1+ My2+ My3+ My4 = min
Теперь все готово для решения задачи. Можно приступить к составлению первой симплексной рис. (2.41), которая будет иметь точно такой же вид, как и в задачах, рассмотренных ранее.
Рис. 2.41. Первая симплекс-таблица
В первоначальную программу войдут все искусственные переменные. Однако есть и некоторая особенность таблицы, заключающаяся в том, что в задачу входит неопределенное число М. Строка М формируется как отрицательная сумма предыдущих строк: столбец В -
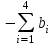; столбцы х1–х9 - 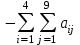.Далее выбираем разрешающий столбец, но поскольку задача решается на минимум, в строке F выбираем положительные элементы, а строке М – максимальный по модулю отрицательный элемент (за исключением столбца В). Таким образом выбран столбец 1 (х1).
Далее, оцениваем отношения элементов столбца В к элементам разрешающего столбца (bi/Aqi), и выбираем большее положительное значение (строка 3 – y3). После этого по аналогичному алгоритму, рассмотренному ранее, пересчитываем вторую таблицу (рис. 2.42)
Рис. 2.42 Вторая симплекс-таблица
В этой таблице разрешающий столбец – 4 (х4), а разрешающая строка – 4 (y4). Переходим к расчету третьей и т.д. таблицам (рис. 2.43-2.45).
Рис. 2.43 Третья симплекс-таблица
Рис. 2.44 Четвертая симплекс-таблица
На пятой итерации (рис. 2.45) получаем в строке М все нули, а все искусственные переменные y1- y4 замещены на основные и базисные переменные х.
Рис. 2.45 Пятая симплекс-таблица
Следовательно, получаем оптимальное решение F-206,67=0, или F=206,67, при х1=66,667, х3=333,33, х4=200. Значение х6=33,33 показывает насколько первое ограничение превышает значение ресурса 500.