Рассмотрим второе ограничение:

3x₁+2x₂<=6

3x₁+2x₂ =6 (2)

x₁=0,следовательно, x₂=3: координаты (0; 3).

x₂=0, следовательно, x₁=2: координаты (3; 0)

Рассмотрим третье ограничение:

x₁+x₂<=1

x₁+x₂ =1 (3)

x₁=0, следовательно, x₂=1: координаты (0; 1)

Если x₂=0, то x₁=-1, но мы рассматриваем только первый квадрант, поэтому возьмем другую точку, например, x₁=1, тогда x₂=2: координаты (1; 2)

Отложим полученные точки на числовых осях и найдем полуплоскости, которые соответствуют первым трем ограничениям (на рисунке они указаны стрелками). Заштрихованная область ОАВСD - область допустимых решений функции F (рис. 2.2).



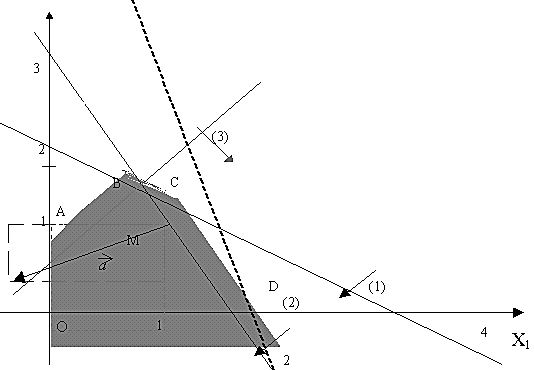
Рис. 2.2. Графический метод решения примера 2

Построение прямой уровня.

Возьмем произвольную точку, принадлежащую области допустимых решений - ОАВСD, например, точку М с координатами (1; 1). Подставим координаты точки М в функцию F.

Получается F(1; 1)=-3*1 - 1=- 4.

Прямая уровня будет иметь следующий вид: -3x₁ - x₂=- 4

Найдем две точки этой прямой - (1; 1) и (0; 4) (если x₁=0, то x₂=4). Построим прямую уровня. Вектор а{-3; - 1}, отложенный от точки М указывает направления возрастания функции F. Минимизируем данную функцию F.

Минимизация целевой функции F.

Так как построенный вектор - является вектором а, указывающем направление возрастания функции F, то передвижение прямой уровня в направлении, обратном вектору а позволит нам найти точку минимума. В нашем случае - это точка D. Координаты точки D равны (2; 0)

Подставляя кординаты точки минимума в функцию F, получим

F(2; 0)= -3*2 - 0= - 6

Ответ: Минимум функция F равен - 6, и он достигается в точке с координатами (2;0)

Теперь исследуем вопрос о разрешимости двумерной задачи линейного программирования. Исследуем вначале область допустимых решений. Понятно, что область допустимых решений существует только тогда, когда ограничения не противоречивы. Если ограничения противоречивы, то область допустимых решений не существует, следовательно, данная задача не имеет решений.

Пример 3

Решить графическим способом следующую двумерную задачу линейного программирования:

---

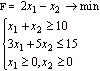
Решение:

Построение области допустимых решений целевой функции F (рис. 2.3).



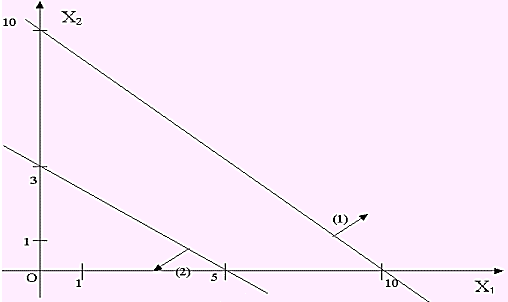
Рис. 2.3. Пример 3

Первое ограничение:

x₁+x₂>=10

x₁+x₂ = 10 (1)

При x₁=0 x₂=10 (0; 10)

При x₂=0 x₁=10 (10; 0)

Второе ограничение:

3x₁+5x₂>=15

3x₁+5x₂ = 15 (2)

При x₁=0 x₂=5 (0; 5)

При x₂=0 x₁=3 (3; 0)

Ограничения задачи противоречивы, поэтому области допустимых решений не существует, следовательно, данная задача неразрешима.

Рассмотрим случай, когда область допустимых решений существует. Здесь возможны два варианта:

1. 
   Область допустимых решений ограниченна со всех сторон (примеры №1,2);
   
2. 
   Область допустимых решений неограниченна с какой-либо стороны.
   

Примечание - Область допустимых решений всегда является выпуклым множеством. Множество S называется выпуклым, если для любых двух точек M и N этого множества весь отрезок MN содержится в множестве S. На рисунке 2.4 изображены примеры выпуклых (а) и невыпуклых (б) множеств.

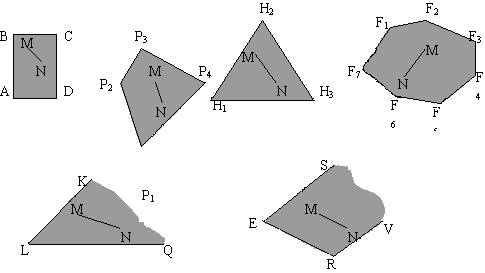а)

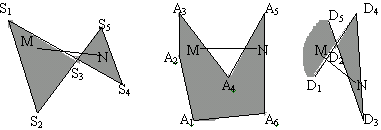б)

Рис. 2.4. Примеры множеств

Если область допустимых решений ограничена (она представляет собой замкнутый выпуклый N - угольник), то задача разрешима и экстремальное значение достигается в какой - либо вершине области допустимых решений. Исключение составляет тот случай, когда прямая уровня параллельна одной из сторон области допустимых решений, и по условию задачи ее надо перемещать именно в направлении этой стороны. Тогда оптимальное решение будет достигаться в любой точке, принадлежащей данной стороне.

Рассмотрим этот случай на примере.

---

Пример 4

Решить графическим способом следующую двумерную задачу линейного программирования:



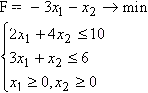
Решение

Построение области допустимых решений целевой функции F.

Построим прямоугольную систему координат. Так как, x₁ и x₂ неотрицательны, то можно ограничится рассмотрением первого квадранта (рис 2.5).



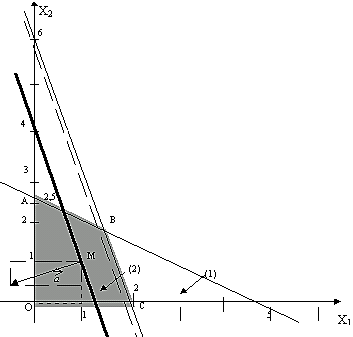
Рис.. 2.5. Пример 4

Рассмотрим первое ограничение:



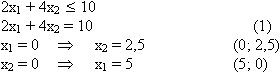
Рассмотрим второе ограничение:



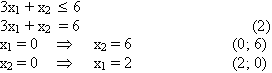
Отложим полученные точки на числовых осях и найдем полуплоскости, которые соответствуют первым трем ограничениям (на рисунке они указаны стрелками). Заштрихованная область ОАВС - область допустимых решений функции F.

Построение прямой уровня.

Возьмем произвольную точку, принадлежащую области допустимых решений - ОАВС, например, точку М с координатами (1; 1). Подставим координаты точки М в функцию F.

F(1; 1)=-31 - 1=- 4

Прямая уровня будет иметь следующий вид: -3x₁ - x₂=- 4

Найдем две точки этой прямой - (1; 1) и (0; 4) (если x₁=0, то x₂=4). Построим прямую уровня. Вектор a{-3; - 1}, отложенный от точки М указывает направления возрастания функции F. Минимизируем данную функцию F.

Минимизация целевой функции F.

Так как построенный вектор a - является вектором, указывающем направление возрастания функции F, то передвижение прямой уровня в направлении, обратном вектору a позволит нам найти точку минимума. Но так как прямая уровня параллельна прямой (2), то любая точка на отрезке ВС является оптимальным решением. В частности в вершинах В(1,5 ; 1,5) и С(2; 0).

F(1,5; 1,5)= F(2; 0) = - 6

Ответ: Минимум функции F равен - 6, и он достигается в любой точке, принадлежащей отрезку ВС.

Пример 5

Решить графическим способом следующую двумерную задачу линейного программирования:

---

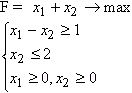
Решение:

Построение области допустимых решений целевой функции F.

Построим прямоугольную систему координат. Так как, x₁ и x₂ неотрицательны, то можно ограничится рассмотрением первого квадранта (рис 2.6).

Рассмотрим первое ограничение:



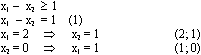
Рассмотрим второе ограничение:



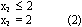
x₂ =2 - прямая, проходящая через точку (0; 2) параллельно оси X₁.

Отложим полученные точки на числовых осях и найдем полуплоскости, которые соответствуют первым двум ограничениям (на рисунке они указаны стрелками). Заштрихованная область АВСD - область допустимых решений функции F.



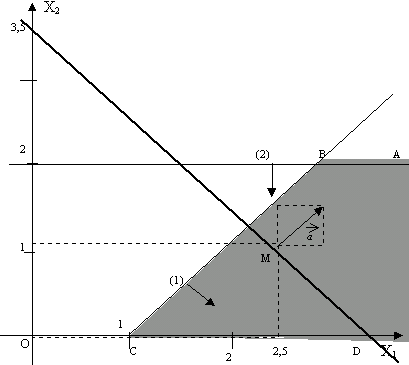
Рис. 2.6. Пример 5

Построение прямой уровня.

Возьмем произвольную точку, принадлежащую области допустимых решений - АВСD, например, точку М с координатами (2,5; 1).

F(3; 1)=2,5+1=3,5

Прямая уровня будет иметь следующий вид: x₁+x₂=3,5

Найдем две точки этой прямой - (2,5; 1) и (0; 3,5) (если x₁=0, то x₂=3,5). Построим прямую уровня. Вектор а {1; 1}, отложенный от точки М указывает направления возрастания функции F. Максимизируем данную функцию F.

Максимизация целевой функции F.

Так как область допустимых решений неограниченна в направлении, в котором функция F возрастает, то не существует конечной точки, в которой функция F достигала бы максимума. Таким образом, данная задача не имеет решений.

Ответ: Задача не имеет решений.

Примечание - Если бы в рассмотренной выше задачи требовалось минимизировать функцию, при тех же ограничениях, то минимум достигался бы в единственной точке С(1; 0) и был бы равен 1.

Таким образом, если область допустимых решений неограниченное множество, то задача может иметь решение, а может и не иметь. Это зависит от того, в каком направлении возрастает (убывает) функция F, и совпадает ли это направлению с направлением неограниченности области допустимых решений.

Вывод: При решении двумерных задач линейного программирования возможны следующие ситуации (ОДР - область допустимых решений) (рис. 2.7):

---

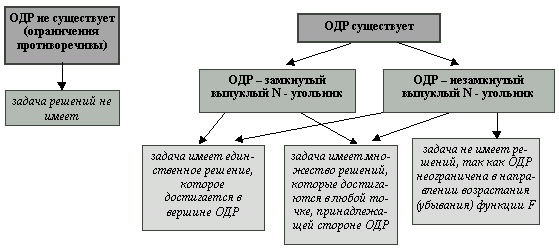
Рис. 2.7. Ситуации ОДР

Пример 6

Построить математическую модель формирования плана производства. Решить ее графическим методом.

Имеется производство по изготовлению двух видов продукции А и В при ограниченном объеме материалов трех сортов, из которых производится продукция. Исходные данные приведены в таблице.



Определить объем производства продукции, обеспечивающий получение максимальной прибыли.

Построение математической модели.

Пусть x₁ - количество продукции вида А, а x₂ - количество продукции В. Тогда

x₁+4x₂ - количество материала сорта 1, требуемое на изготовление продукции, а по условию задачи это число не превышает 320

x₁+4x₂<=320 (1)

3x₁+2x₂ - количество материала сорта 2, требуемое на изготовление продукции, а по условию задачи это число не превышает 360

3x₁+2x₂<=360 (2)

x₁+2x₂ - количество материала сорта 2, требуемое на изготовление продукции, а по условию задачи это число не превышает 180

x₁+2x₂<=180 (3)

Кроме того, поскольку x₁ и x₂ выражают объем выпускаемых продукции, то они не могут быть отрицательными, то есть

x₁>=0, x₂>=0 (4)

F=x₁+2x₂ - прибыль, которая должна быть максимальной. Таким образом, имеем следующую математическую модель для данной задачи.



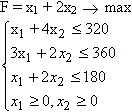
Решение:

Построение области допустимых решений целевой функции F.

Построим прямоугольную систему координат. Так как, x₁ и x₂ неотрицательны, то можно ограничится рассмотрением первого квадранта.

Рассмотрим первое ограничение:



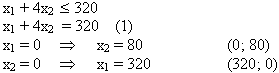
Рассмотрим второе ограничение:



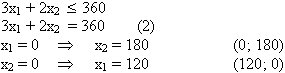
Рассмотрим третье ограничение:

---

Смотрите также файлы

• 3 Социальнопсихологический тренинг общения.doc

• Приоритетные направления начального общего образования в рамках реализации Федерального государственного образовательного стандарта второго поколения.doc

• Едеральное агентство по техническому регулированию и метрологии н ациональный.doc

• Практическая работа Использование библиотеки цифрового образовательного контента в учебной деятельности.docx

• Минобрнауки россии санктПетербургский государственный.docx