В задаче требуется найти оптимальный план раскроя ДСП, обеспечивающий выход планового числа заготовок при минимальных суммарных отходах от раскроя всех плит. Иными словами, в задаче необходимо определить, сколько ДСП следует раскроить по тому или иному варианту раскроя, чтобы нарезать требуемое число заготовок и при этом отходы были бы минимальными.

Математическая модель задачи, заключающаяся в минимизации целевой функции

F=0,5x₁+0,6x₂+0,4x₃+0,2x₄+0,3x₅ (2.8)

при ограничениях, представленных в виде системы линейных неравенств:

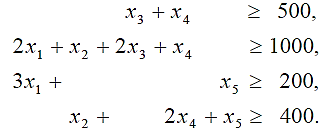(2.9)

при x _j ≥0 (j =1,2,3,4,5)

или то же в общем виде

F=c₁x₁+ c₂x₂+…+ c_nx_n.= min (2.10)

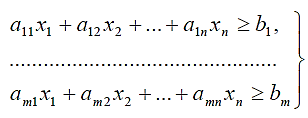(2.11)

при x _j ≥0 ( j =1,2,..., n) и

при b_i ≥0 (i =1,2,..., m).

Эти исходные неравенства надо преобразовать в равенства с неотрицательными неизвестными. Для этого надо ввести дополнительные неотрицательные неизвестные х₆, x₇, х₈ и x₉ (а в общем случае x_n+1, х_п+2,…,х_п+т) в неравенства-ограничения так, чтобы

---

они превратились в уравнения.

В данной задаче неравенства имеют противоположный смысл по сравнению с неравенствами, рассмотренными ранее, т. е. левые части должны быть не менее правых частей, поэтому дополнительные неотрицательные неизвестные должны вводиться со знаком плюс в правые части неравенств, либо со знаком минус (с коэффициентами -1) в левые части этих неравенств-ограничений.

Итак, вышеуказанные системы неравенств, преобразуются в следующие эквивалентные системы линейных уравнений:

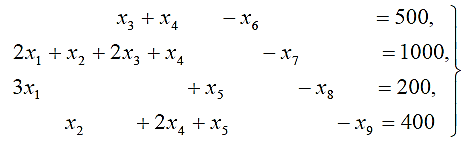(2.12)

F=0,5x₁+0,6x₂+0,4x₃+0,2x₄+0,3x₅-0x₆-0x₇-0x₈-0x₉=min при x_j≥0 (2.13)

или, в общем виде,

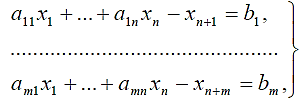(2.14)

F=c₁x₁+…+ c_nx_n.+0x_n+1+…+0x_n+m= min. (2.15)

В матрицах систем уравнений такого вида не содержится единичной подматрицы, в которой диагональные элементы были бы равны единице, а остальные - нулю. В них содержатся подматрицы,

---

соответствующие дополнительным неизвестным, с диагональными элементами, равными -1. Поэтому, если принять дополнительные неизвестные в качестве базисных, то они окажутся отрицательными (х₁ = х₂ = х₃ = х₄ = x₅ = 0, х₆= -500, х₇ = -1000, х₈ = -200, x₉ = -400), т. е. не будут удовлетворять условиям неотрицательности всех переменных. Следовательно, здесь мы не имеем явной неотрицательной исходной программы.

Для решения задачи необходима единичная подматрица (с положительными элементами). Чтобы получить ее, надо ввести еще одну группу неизвестных, число которых равно числу исходных неравенств (или уравнений), по одному такому неизвестному на каждое неравенство (или уравнение). Эти новые неизвестные в отличие от дополнительных - уравновешивающих — называют

---

искусственными. В данной задаче обозначим их через y₁, у₂, у₃, y₄ и введем их в левые части уравнений со знаком плюс.

Симплексные уравнения исходных условий в окончательном виде, допускающем перенесение коэффициентов при неизвестных непосредственно в первоначальную симплекcную таблицу, будут¹:

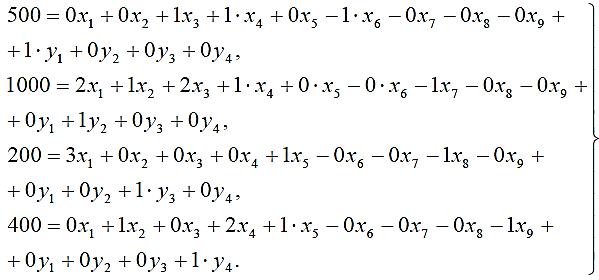(2.16)

В этих уравнениях имеется единичная подматрица и все неизвестные считаются неотрицательными. Дальнейшее решение задачи может быть выполнено двумя способами.

Первый способ заключается в отыскании какой-то программы (опорного плана) основной задачи (2.8), (2.9) посредством решения вспомогательной задачи,которая заключается в нахождении минимума целевой функции:

F’=y₁+ y₂+ y₃+y₄=min (2.17)

или, в расширенном виде,

F’=0x₁+0x₂+0x₃+0x₄+0x₅+0x₆+0x₇+0x₈+0x₉+1y₁+1y₂+1y₃+1y₄=min

Если получится минимум этой целевой функции, равный нулю (F' = 0), то в решении этой вспомогательной задачи (3.24; 3.25) получится искомая программа исходной задачи (3.16; 3.17).

Второй способ решения этой задачи. Он в значительной мере отличается от первого хотя бы тем, что здесь не требуется решать вспомогательную задачу для отыскания опорного плана (какого-то решения) исходной задачи. Этот способ позволяет нам приступить к непосредственному решению исходной задачи, поскольку в симплексных уравнениях, представленных в окончательной форме, имеется единичная подматрица (2.16).

---

Целевая функция была представлена выражением (2.8):

F=0,5x₁+0,6x₂+0,4xз+0,2x₄+0,3x₅=min

Искусственные переменные у₁, y₂, y₃ и y₄ входят в первоначальную программу, с которой начинается процесс решения задачи, как базисные с положительными значениями, но по ходу решения они постепенно исключаются из базисных переменных. Оптимальной программа станет не раньше, чем все эти искусственные переменные перейдут из базисных в свободные. Чтобы это обеспечить, искусственные неизвестные вводятся в уравнение целевой функции с коэффициентами (ценами), равными М.

Под Мпонимается величина больше любого другого сколько угодно большего наперед заданного числа. Таким образом, мы блокируем искусственные неизвестные, т. е. введением коэффициентов Ммы избавляемся от влияния искусственных переменных на истинную оптимальную программу. Действительно, как только хотя бы одна из искусственных переменных в программе положительна, значение целевой функции расширенной задачи (с искусственными переменными), соответствующим подбором положительного числа М, может быть сделано больше любого значения целевой функции (2.8) исходной задачи при любых значениях основных переменных х₁, x₂, x₃, x₄, х

---

Смотрите также файлы

• 3 Социальнопсихологический тренинг общения.doc

• Приоритетные направления начального общего образования в рамках реализации Федерального государственного образовательного стандарта второго поколения.doc

• Едеральное агентство по техническому регулированию и метрологии н ациональный.doc

• Практическая работа Использование библиотеки цифрового образовательного контента в учебной деятельности.docx

• Минобрнауки россии санктПетербургский государственный.docx