Продажная цена трех продуктов соответственно 9, 13 и 11 руб.

Расход материалов на единицу продукции, а также фонд использования материалов приведены в таблице.

Вид материала	Расход материалов на 1 продукт			Фонд использования материала
	Продукт1	Продукт2	Продукт3
Материал1	4	5	4		770
Материал2	5	3	6		830

Себестоимость единицы продукции 4, 5 и 3,5 руб.

Объем выпуска Продукта3 не может превышать объем выпуска Продукта1 более чем на 50.

Найти план выпуска продукции, при котором общая себестоимость будет не более 700 руб., прибыль максимальной.

* Выпуск Продукта2 должен быть не менее 60.

Вариант № 26

Организация производит два вида продукции – Прод1 и Прод2. Объём производства продукции Прод1 и Прод2 составляет не более 200 каждого вида.

Для изготовления продукции Прод1 и Прод2 используется одно и тоже сырьё, суточный запас которого ограничен величиной 140 кг.

Расход сырья на единицу продукции Прод1 составляет 3 кг, а на единицу продукции Прод2 - 5 кг.

Нормы затрат на производство единицы каждого вида продукции на оборудовании составляют соответственно 4 и 3. Фонд времени оборудования составляет 1200 ч.

Цены продукции Прод1 и Прод2 равны 30 и 40 руб., соответственно.

Определить оптимальное распределение сырья для изготовления продукции Прод1 и Прод2, позволяющее получить максимальную выручку от продажи продукции.

* Выпуск Прод2 должен быть не менее 200.

Вариант № 27

Для производства четырех видов конфет используются следующие виды сырья: сахарный песок, какао и патока.

Нормы расхода сырья на производство 1 тонны конфет каждого вида и запасы сырья каждого вида приведены в таблице.

Вид сырья	Нормы расхода сырья на 1 т конфет					Запасы сырья
	Конфеты1	Конфеты2	Конфеты3	Конфеты4
Сахарный песок	1,0	0,9	1,10	1,50	750
Какао	0,3	0,2	0,25	0,35	250
Патока	0,5	0,6	0,70	0,75	450

---

Прибыль от реализации 1т конфет Конфеты1 – 2,7 тыс. руб., Конфеты2 – 2,5 тыс. руб., Конфеты3 – 3 тыс. руб., Конфеты4 – 4, 1 тыс. руб.

Найти план производства конфет, обеспечивающий максимальную прибыль от реализации.

* Выпуск Конфет3 должен составлять не менее 150т.

Вариант № 28

Предприятие выпускает радиоприёмники трёх различных моделей: "Турист", "Альпинист", "Сокол".

Каждое из указанных изделий приносит доход в размере 13, 16, 25 руб. соответственно. Каждая модель характеризуется определённым временем, необходимым для изготовления деталей, временем сборки изделия и его упаковки, представленным в таблице.

Изделия	Сборка, ч.	Изготовление, ч.	Упаковка, ч.
"Турист"	3,65	3	1
"Альпинист"	4	3,5	1,5
"Сокол"	5	8	3

В течение ближайшей недели предприятие может израсходовать на производство радиодеталей 150 часов, на сборку - 200 часов и на упаковку - 60 часов. Определить план выпуска радиоприёмников с целью получения максимальной прибыли.

* Выпуск приемников "Альпинист" должен составлять не менее 5.

Вариант № 29

При производстве двух видов продукции А и В предприятие использует четыре группы оборудования.

Для производства единицы продукции А используется в течение смены 1, 0.5, 2 и 0 единиц I, II, III и IV видов оборудования соответственно. Для производства единицы продукции В используется в течение смены 1, 1, 0 и 2 единиц I, II, III и IV видов оборудования соответственно. Производственные мощности предприятия: оборудование 1 группы - 18 единиц, П 12, III - 24, IV - 18.

Предприятие получает доход от реализации единицы продукции А в размере 4 руб. И от реализации продукции В - 6 руб.

Составить план производства, обеспечивающий максимальную прибыль.

* Продукции В необходимо производить не менее 8.

Вариант № 30

Предприятие располагает четырьмя группами станков, на которых планируется изготовление четырех изделий. При этом фонд рабочего времени каждой группы станочного парка составляет: по станкам групп А - 300 ч ; по станкам группы Б - 260 ч.; по станкам группы В - 280 ч.; по станкам группы Г - 260 ч. Время изготовления каждого изделия соответственно на каждой группе станков приведено в таблице.

---

Вид изделия	Время изготовления для групп станков(час)
	А	Б	В	Г
Изд1	1	4	1	2
Изд2	0	4	2	2
Изд3	5	0	3	3
Изд4	2	4	0	0

Стоимость изделий соответственно составляет: 8, 8, 11 и 6 руб.

Определить программу изготовления изделий, при которой обеспечивается максимально прибыль.

* Выпуск Изд1 должен составлять не менее 10.

---

Приложение 1.

Симплексный метод в решении задач с условием в виде уравнений и неравенств со знаком «≥» (метод искусственного базиса).

Ранее был рассмотрен основной алгоритм симплексного метода для решения так называемой стандартной задачи линейного программирования на максимум целевой функции, условие которой было представлено в виде неравенств с положительными свободными членами.

Исходные неравенства нами были преобразованы в уравнения путем ввода дополнительных неотрицательных неизвестных (x_n+1,…,х_п+т). Дополнительные неизвестные входили в симплексные уравнения со знаком плюс, и в единичной подматрице на главной диагонали мы имели элементы, равные единице. Это позволило нам получить исходную программу.

В целом ряде экономических задач исходные ограничительные условия могут быть представлены в виде уравнений или неравенств с любыми знаками:



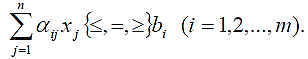
Предположим, дано условие задачи в виде системы линейных уравнений:

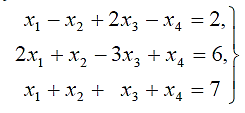(2.4)

и требования минимизации целевой функции

F(x)=2x₁+x₂-x₃-x₄ (2.5)

при неотрицательных переменных x₁, x₂, x₃ и x₄ или то же в общем развернутом виде:

---

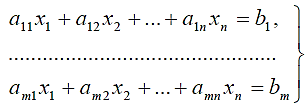
(2.6)

при bi≥0, i = l , 2, . . ., mи при x_j ≥0, j=1,2,…,nи минимизации целевой функции

F=c₁x₁ + c₂x₂+…+ c_nx_n. (2.7)

Как в числовом примере, так и в общей формулировке задачи нет таких переменных x_j, которые бы входили с коэффициентом + 1 один раз в какое-либо одно уравнение системы.

Следовательно, нет и явной исходной программы.

Рассмотрим еще один пример — раскройную задачу.

Условие задачи. Положим, что на мебельном комбинате производится раскрой ДСП на заготовки и детали для мебели. Известно, что из партии ДСП необходимо нарезать четыре вида (А, В,С,D)различных по размерам заготовок и деталей. Древесностружечная плита стандартных размеров может быть раскроена пятью способами (вариантами). По каждому возможному варианту раскроя составляется соответствующая карта раскроя. Из карт раскроя известен выход заготовок (в штуках) раз- ных размеров, а также площадь отходов при раскрое одной плиты по тому или иному варианту.

В задании на раскрой указано общее количество заготовок каждого вида, которые необходимо нарезать из партии плит, поступивших в раскрой. Все эти данные приведены в табл. 1.3.

Табл. 1.3

Виды (типоразмеры) заготовок и деталей	Задание на раскрой по выходу заготовок, шт.	Выход заготовок, шт., по видам, при раскрое одной плиты по вариантам
		1		2		3		4		5
А	500	0		0		1		1		0
В	1000	2		1		2		1		0
С	200	3		0		0		0		1
D	400	0		1		0		2		1
Площадь отходов, м2			0,5		0,6		0,4		0,2		0,3

---

Смотрите также файлы

• 3 Социальнопсихологический тренинг общения.doc

• Приоритетные направления начального общего образования в рамках реализации Федерального государственного образовательного стандарта второго поколения.doc

• Едеральное агентство по техническому регулированию и метрологии н ациональный.doc

• Практическая работа Использование библиотеки цифрового образовательного контента в учебной деятельности.docx

• Минобрнауки россии санктПетербургский государственный.docx