Файл: Ю. Ф. Королюк Контрольные задания и задачи рейтингового контроля по курсу Теоретические основы электротехники.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 97

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Контрольные задания и задачи рейтингового контроля

КОНТРОЛЬНОЕ ЗАДАНИЕ

(где  – длина волны). Волновое сопротивление линии ZC.

4%

12. Определить входное сопротивление Zвх линии без потерь при холостом ходе длиной в (где  – длина волны). Волновое сопротивление линии ZC.

4%

13. Определить, на каком минимальном расстоянии должна быть закорочена линия без потерь с волновым сопротивлением ZC, чтобы ее входное сопротивление стало равным jZC.

4%

14. Линия без потерь имеет длину l, волновое сопротивление ZC, коэффициент фазы . В конце линии включена индуктивность L2. Найти, на каком расстоянии х от конца линии будет ближайшая пучность напряжения, если напряжение в конце линии u2 = U2msint.

4%

15. Двухпроводная линия длиной l = 100 км имеет при частоте  = рад/с вторичные параметры: ZC = 300 Ом, 1/км.

Определить значения индуктивности L и емкости С П–образной схемы замещения линии.

4%

16. Длина двухпроводной линии без потерь меньше четверти длины волны. При нагрузке линии на активное сопротивление r2 отношение действующих значений напряжений в начале и в конце линии , а при холостом ходе – 0,5.

Определить входное сопротивление линии Zвх при коротком замыкании на конце.

4%

17. Трехфазная воздушная линия электропередачи характеризуется вторичными параметрами на фазу: ZC = 390 Ом, l = j1,05. На конце линии включена трехфазная активно–индуктивная нагрузка, потребляющая мощность Р2 = 100 МВт при cos2 = 0,9. Линейное напряжение в конце линии U2 = 380 кВ.

Определить величину линейного напряжения U1 и тока I1 в начале линии.

4%

18. Однородная линия без потерь с волновым сопротивлением ZC, волновой скоростью v и длиной l на конце замкнута накоротко. Линия подключается к источнику ЭДС U0.

Определить напряжение u и ток i в конце линии через время после момента включения.

8%

19. Однородная линия без потерь с волновым сопротивлением ZC, волновой скоростью
v и длиной l разомкнута на конце. Линия подключается к источнику ЭДС U0.

Определить напряжение u и ток i в конце линии через время после момента включения.

8%

20. Воздушная линия без потерь длиной l = 90 км с волновым сопротивлением ZC = 400 Ом, волновой скоростью км/с разомкнута на конце. Линия подключается к источнику постоянного напряжения U0 = 120 кВ.

Определить напряжение u и ток i в линии через 1,2 мс после момента включения.

8%

21. Кабельная линия без потерь длиной l = 12 км с волновым сопротивлением ZC = 60 Ом, волновой скоростью км/с замкнута накоротко на конце. Линия подключается к источнику постоянного напряжения U0 = 15 кВ.

Определить напряжение u и ток i в линии через 240 мкс после коммутации.

8%

22. Волна напряжения uпад переходит с линии с волновым сопротивлением ZС1 = 3ZС на линию с волновым сопротивлением ZС2 = ZС (обе линии однородны и без потерь).

Определить коэффициент преломления ku волны напряжения и коэффициент преломления ki волны тока в месте соединения линий.

6%

2. Контрольные задания
2.1. Контрольное задание № 1.

Задача 1. Дана электрическая цепь, в которой происходит коммутация. В цепи действует постоянная ЭДС Е. Параметры цепи приведены по вариантам в таблице 2.1. Требуется определить закон изменения во времени тока после коммутации в одной из ветвей схемы или напряжения на каком–либо элементе или между заданными точками схемы.

Задачу следует решить двумя методами: классическим и операторным. На основании полученного аналитического выражения построить график изменения искомой величины в функции времени в интервале от t = 0 до t = , где – меньший по модулю корень характеристического уравнения.

Таблица 2.1.

Исходные данные по вариантам к задаче 1

контрольного задания 1.

Вариант
Рисунок
Е, В
L, мГн
С, мкФ
R1
R2
R3
R4
Определить

Ом

1
2.5
100
1
10
20
15
5
2
i

2
2.2
150
2
5
8
10
5
2
i1

3
2.19
100
1
10
2
2






i1

4
2.10
120
1
10
3
0
1
1
i1

5
2.3
100
5
50
2
8
6



i1

6
2.1
50
1
1500
2
13
1
4
i1

7
2.11
120
10
10
10
90
1000
1000
i1

8
2.18
200
1
20
4
4
2



i3

9
2.4
100
1
10
50
25
25



uC

10
2.17
300
5
4
10
20
10
20
uC

11
2.20
100
1
10
20
4
16
2


12
2.15
150
4
5
6
10
5
4
uC

13
2.6
30
1
2,5
10
10
10



uC

14
2.7
200
10
10
100
0
50
100
i1

15
2.12
100
1
10
10
10
4



i1

16
2.16
50
2
1670
1
2
1
5
i1

17
2.8
120
10
10
10
90
1000
1000
i1

18
2.13
120
1
10
8
8
8
4
i1

19
2.9
200
1
10
10
20
50
20
i1

20
2.14
50
1
100
2
8
10
10
i1

21
2.5
100
1
10
20
20
0
2
uL

22
2.2
150
2
5
5
10
5
5
i2

23
2.19
100
1
10
1
3






i3

24
2.10
120
1
10
1
2
1
1
i2

25
2.3
100
5
50
3
8
5



uC

26
2.1
50
1
1500
2
13
2
3
i

27
2.11
120
10
10
20
80
1000
1000
i3

28
2.18
200
1
20
6
3
2



i1

29
2.4
100
1
10
50
20
30



uL

30
2.17
300
5
4
15
20
5
20
i2

31
2.20
100
1
10
20
17
3
2
i1

32
2.15
150
4
5
9
10
5
1
uL

33
2.6
30
1
2,5
5
10
15



i3

34
2.7
200
10
10
50
50
50
100


35
2.12
100
1
10
5
15
4



uL

36
2.16
50
2
1670
1
2
2
4
i2

37
2.8
120
10
10
20
80
1000
1000
i2

38
2.13
120
1
10
12
6
8
4
i3

39
2.9
200
1
10
10
10
50
30
i2

40
2.14
50
1
100
3
7
10
10
i2


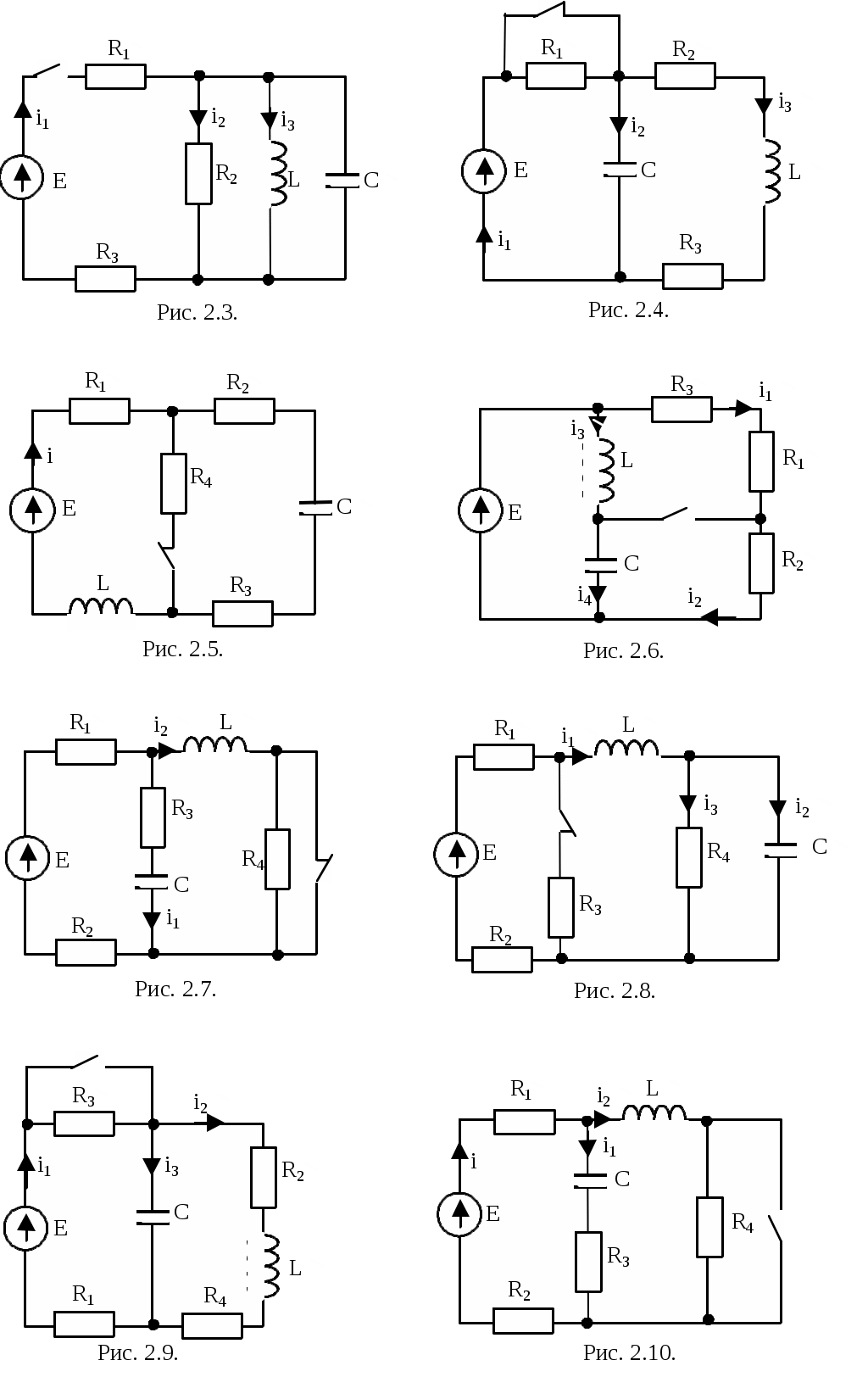
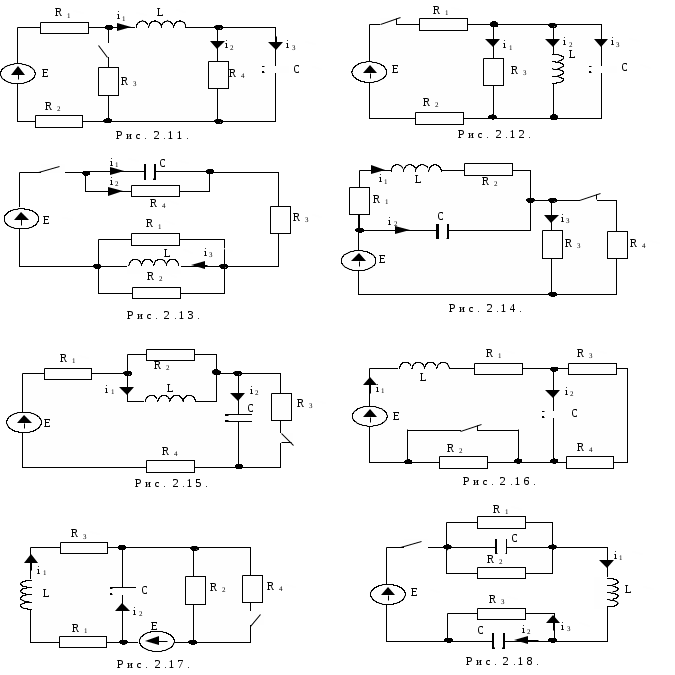
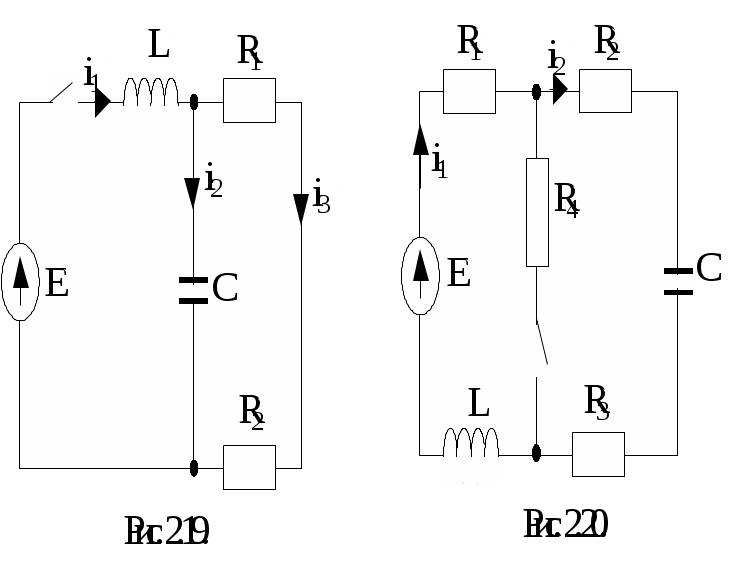
Р
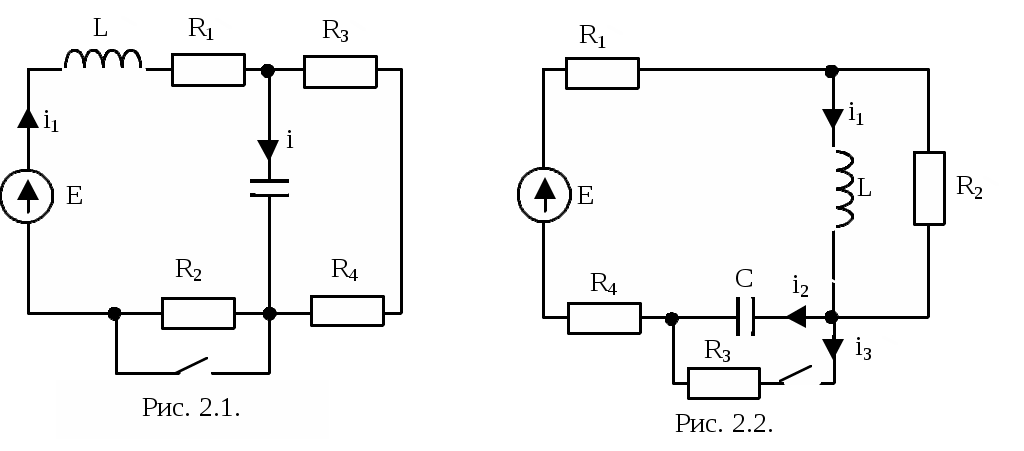
исунки к вариантам задачи 1 контрольного задания 1.












Задача 2. Дана электрическая схема, на входе которой действует напряжение, изменяющееся во времени по данному закону u1(t). Требуется определить закон изменения во времени тока в одной из ветвей схемы или напряжение на заданном участке схемы. В таблице 2.2 в соответствии с номером варианта указан номер рисунка, на котором приведен график изменения во времени входного напряжения Параметры цепи R, L, C заданы в буквенном виде.

Задачу требуется решить с помощью интеграла Дюамеля. Искомую величину следует определить (записать ее аналитическое выражение) для всех интервалов времени. В зависимости от условий задачи полный ответ будет содержать два или три соотношения, каждое из которых справедливо лишь в определенном диапазоне времени.

В каждом ответе следует выполнить приведение подобных членов относительно и выделить постоянную составляющую.

Примечание. На рис. 2.31, 2.32, 2.36 входное напряжение дано с двумя индексами. Первый индекс (индекс 1) указывает на входное напряжение, второй индекс ( 1 или 2) – на интервал времени, о котором идет речь. Так, например, u11 – входное напряжение для первого интервала времени, u12 – входное напряжение для второго интервала времени.

Таблица 2.2

Исходные данные по вариантам к задаче 2

контрольного задания 1.

Вариант
Рисунок с изображением схемы
Рисунок с графиком
Определить
Вариант
Рисунок с изображением схемы
Рисунок с графиком
Определить

1
2.23
2.27
i4
21
2.23
2.28
i4

2
2.22
2.27
uR
22
2.22
2.30
uR

3
2.24
2.27
u2
23
2.24
2.30
u2

4
2.23
2.29
i1
24
2.23
2.30
i1

5
2.21
2.27
i1
25
2.21
2.28
i1

6
2.22
2.28
i2
26
2.22
2.29
i2

7
2.24
2.31
i1
27
2.24
2.32
i1

8
2.25
2.27
i1
28
2.25
2.31
i1

9
2.25
2.30
i2
29
2.25
2.32
i2

10
2.21
2.28
uL
30
2.21
2.29
uL

11
2.24
2.27
i3
31
2.24
2.30
i3

12
2.22
2.27
i3
32
2.22
2.35
i3

13
2.25
2.27
i3
33
2.25
2.30
i3

14
2.22
2.27
uC
34
2.22
2.30
uC

15
2.25
2.28
uL
35
2.25
2.29
uL

16
2.24
2.28
i2
36
2.24
2.29
i2

17
2.23
2.34
uC
37
2.23
2.30
uC

18
2.26
2.31
u2
38
2.26
2.36
u2

19
2.23
2.27
i2
39
2.23
2.34
i2

20
2.23
2.27
i3
40
2.23
2.28
i3

Р
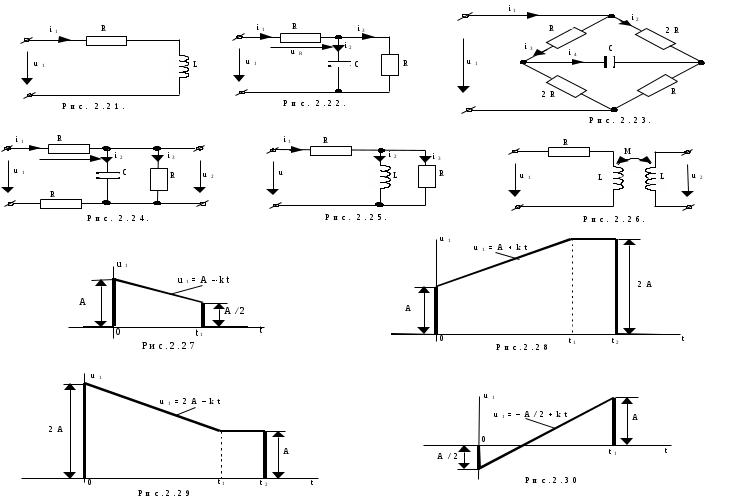
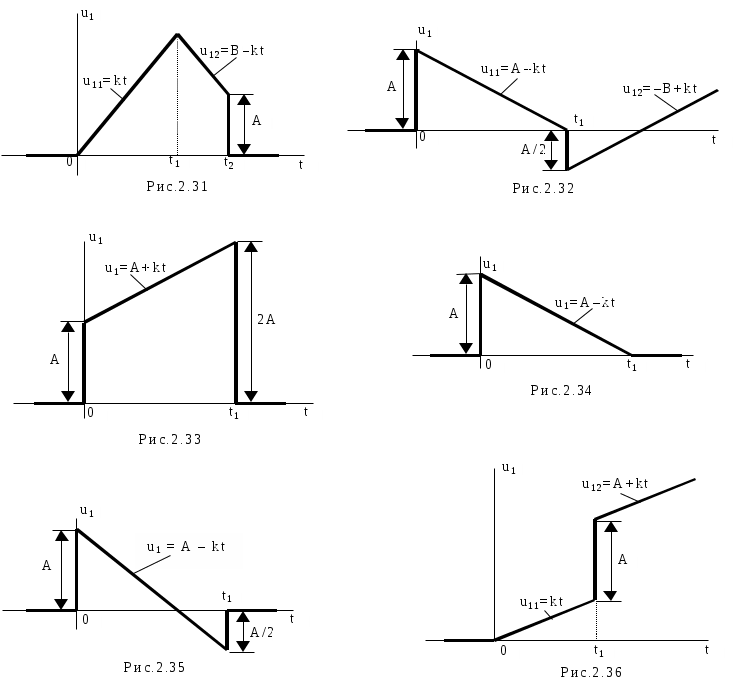
исунки к вариантам задачи 2 контрольного задания 1.



2.2. Контрольное задание № 2.

Задача 1. На рис.2.37 даны схемы, на вход которых воздействует одно из периодических напряжений u(t) (графики напряжений приведены на рис. 2.38 – 2.45). Схемы нагружены на активное сопротивление нагрузки Rн. Численные значения напряжения Um, периода Т, параметров схемы L, C и величины активного сопротивления нагрузки Rн приведены в таблице 2.2. Требуется:

  1. Разложить напряжение u(t) в ряд Фурье до пятой гармоники включительно, используя табличные разложения, приведенные в учебниках, и пояснение, имеющееся в указаниях к данной задаче.

  2. Обозначив сопротивления элементов схемы в общем виде как Rн, jXL, –jXС, вывести формулу для комплексной амплитуды напряжения на нагрузке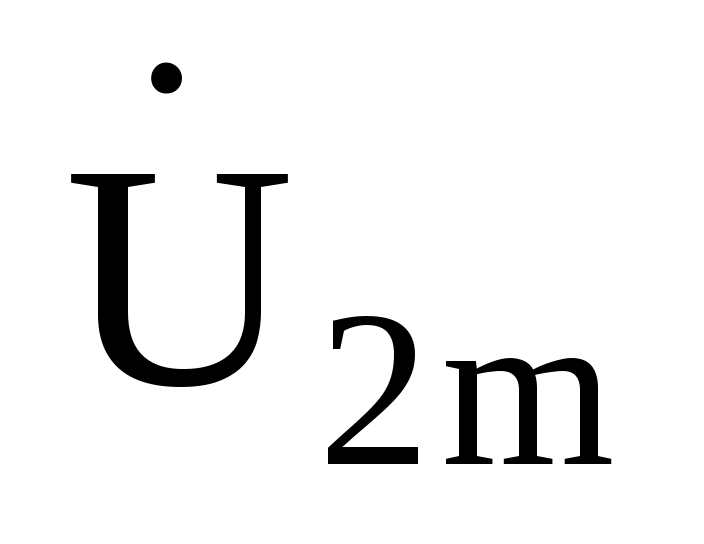 через комплексную амплитуду входного напряжения 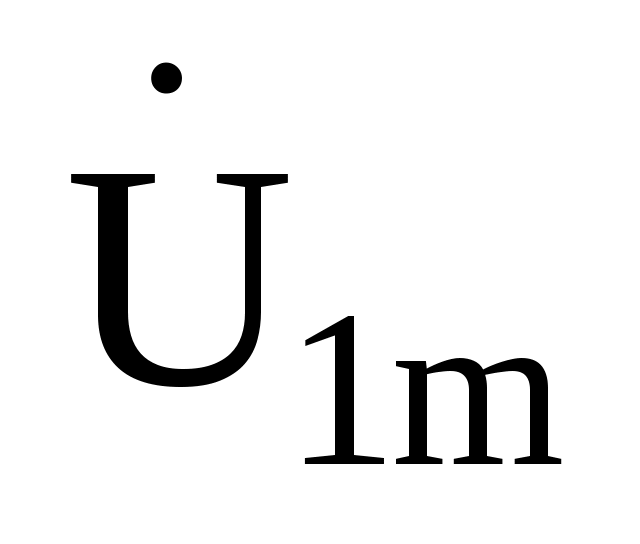. Полученное напряжение пригодно для каждой гармоники, только под XL и XC следует понимать сопротивления для соответствующей гармоники.

  3. Используя формулы п. 2, определить комплексную амплитуду напряжения на выходе (на нагрузке) для следующих гармоник ряда Фурье: для нулевой, первой и третьей гармоник в схемах рис. 2.37,в,г; для первой, третьей и пятой гармоник в схемах рис. 2. 37,а.б.

  4. Записать мгновенное значение напряжения на нагрузке u2 = f(t) в виде ряда Фурье.

У к а з а н и е:

На примере рис. 2.44, 2.45 покажем как осуществляется разложение в ряд Фурье кривых, которые имеют постоянную составляющую и начало которых сдвинуто во времени по отношению к табличным кривым. Прежде всего выделим в напряжении u1(t) (рис.2.45) постоянную составляющую Um/2 и мысленно проведем новую ось времени на высоте Um/2. Тогда относительно новой оси времени оставшуюся часть напряжения запишем в виде

.
Здесь под Um понимается амплитуда заданного напряжения, а угол Т/12 равен углу, обозначенному в учебниках . С учетом постоянной составляющей u1(t) (рис 2.45) раскладывается в ряд Фурье следующим образом:

Смотрите также файлы