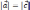Файл: Методическое пособие 1011 классов с. Мичуринское удк 371. 3 Ббк 74. 262. 21 В27 Рецензентты.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 71
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Қостанай облысы Қостатай ауданы әкімдігінің
«Мичурин орта мектебі» ММ
ГУ «Мичуринскаясредняяшкола»
Отделаобразования акимата Костанайского района, Костанайскойобласти
Векторы в пространстве
Методическое пособие
10-11 классов
с. Мичуринское
УДК 371.3
ББК 74.262.21
В27
Рецензентты:
Вельченко О. А Магистр математики, старший преподаватель кафедры социально-гуманитарных и естественнонаучных дисциплин
Костанайского филиала ФГБОУ ВПО
«Челябинский государственный университет»
Альмагамбетова М.К Заместитель директора по учебной работе
ГУ «Мичуринская средняя школа»
Векторы в пространстве: Методическое пособие/сост: З. А. Альмагамбетова.-Костанайскаяобласть, Костанайскийрайон, 2016.- 32.с.
ISBN 978-601-316-177-8
Пособие предназначено для более подробного изучения темы «Векторы в пространстве» по стереометрии за курс 10-11 классов общеобразовательной школы. Данное пособие может быть использовано учителями математики средних школ при обучении школьников решению векторных задач, а также студентами математических специальностей педагогических институтов.
УДК 371.3
ББК 74.262.21
©Альмагамбетова З. А.,2016
Введение.
Данное пособие адресовано в первую очередь тем, кто желает успешно подготовиться к ЕНТ по математике.
Цель нашего пособия - рассмотреть примеры решения некоторых стереометрических задач, предлагаемых на ЕНТ, которые позволят лучше понять и запомнить векторный и координатный способы решения геометрических задач.
Данное пособие включает в себя перечень основных формул на применение координат и векторов при вычислении расстояний, углов, площадей и объёмов в стереометрических задачах. Затем приводятся примеры решения задач различного уровня сложности и упражнения для самостоятельного решения (с ответами). Задания взяты из различных сборников ЕНТ.
Рекомендации по работе с пособием:
-
Внимательно ознакомьтесь со справочным материалом, при необходимости повторите теоретический материал по школьному учебнику или по другим источникам (см. список литературы). Применение основных формул сопровождается иллюстрирующими задачами. -
Прочитав задачу, попытайтесь решить её самостоятельно, не заглядывая в решение, предложенное в пособии. Не исключено, что Ваше решение может оказаться более рациональным или оригинальным. -
Если же задачу не удаётся решить самостоятельно, посмотрите начало решения, указанное в пособии. Возможно, Вам достаточно будет какой-то начальной идеи, чтобы завершить решение самостоятельно. -
Если всё-таки задачу решить не можете, ознакомьтесь с полным решением, предложенным в пособии. После этого обязательно перерешайте разобранную задачу от начала до конца самостоятельно. -
В некоторых задачах предложены несколько способов решения. Разберите каждый! После этого переходите к упражнениям для самостоятельной работы.
Пособие будет полезно не только учащимся старших классов, но и учителям математики. Проанализировав решения, учитель математики сможет более эффективно построить систему учебных занятий. С другой стороны, он будет иметь реальную возможность отбора задач для осуществления контроля за освоением конкретным учеником данной темы.
Векторы на плоскости
| Вектором называется отрезок, у которого указаны начало и конец (т.е. величина, которая характеризуется численным значением и направлением). |  |
Координаты и длина вектора
| Даны точки А(х1;у1) и В(х2; у2) Координаты вектора 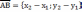 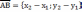 | 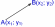 |
| Длина вектора 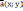 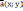 вычисляется по формуле: вычисляется по формуле: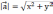 | |
| Координаты вектора не изменяются при параллельном переносе. | |
| Действия над векторами Если 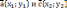 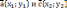 , то , то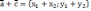 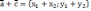 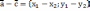 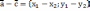 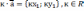 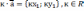 | 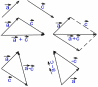 |
| Разложение вектора по координатным векторам Если 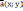 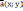 , то , то 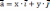 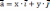 | 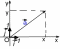 |
| Коллинеарные векторы Коллинеарными называются векторы, лежащие на одной прямой или на параллельных прямых. Условие коллинеарностивекторов 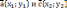 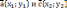 в координатном представлении: в координатном представлении: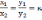 | 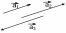 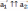 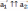 - сонаправленные векторы - сонаправленные векторы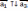 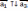 - противоположно направленные векторы - противоположно направленные векторы |
| Равные векторы 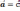 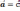 ,если: ,если: 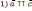 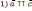 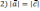 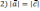 У равных векторов соответствующие координаты равны. Противоположные векторы ( 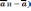 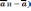 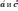 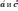 противоположные векторы, если: противоположные векторы, если:Соответствующие координаты противоположны. |   |
| Ортогональные векторы 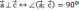 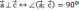 Условие ортогональности (перпендикулярности) векторов, 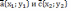 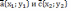 на плоскости: на плоскости: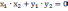 | 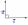 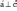 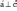 - ортогональные векторы - ортогональные векторы |
| Скалярное умножение векторов Скалярным произведением двух векторов 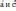 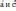 называетсячисло, равное произведению длин этих векторов на косинус угла между ними : называетсячисло, равное произведению длин этих векторов на косинус угла между ними :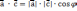 Скалярное произведение векторов 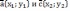 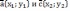 выражается через координаты: выражается через координаты: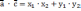 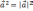 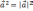 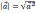 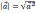   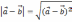 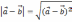 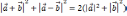 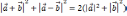 | 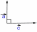 =900 =900 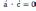 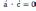  00≤900 00≤900 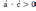 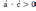 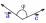 900≤1800 900≤1800 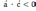 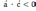 |
| Применение скалярного произведения к решению задач 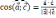 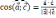 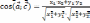 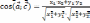 | |
Метод координат в пространстве
| Прямые x, y, z называются координатными осями (или осями координат), Оси координат обозначаются так: OX- ось абсцисс OY- ось ординат OZ- ось аппликат точка их пересечения O – началом координат, а плоскости xOy, xOz и yOz – координатными плоскостями. В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами. М(x; y; z). | Прямоугольная система координат в пространстве 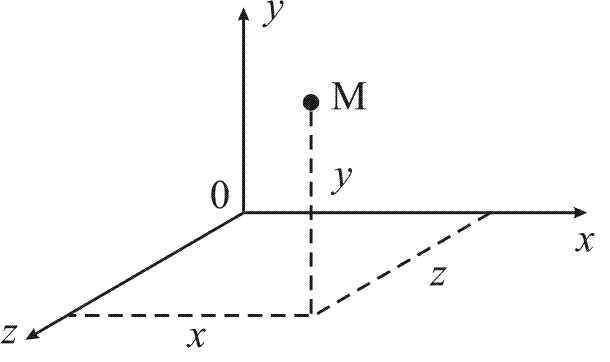 |
| Действия над векторами: |
| Сложение векторов 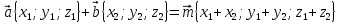 |
| Вычитание векторов 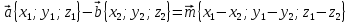 |
| Умножение вектора на число k. 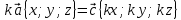 |
| Координаты середины отрезка AB: А(x1;y1;z1), B(x2;y2;z2). Точка М середина отрезка AB. 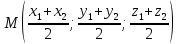 |
| Вычисление длины вектора 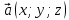 по его координатам: по его координатам: 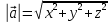 |
| Расстояние между двумя точками. А(x1;y1;z1) и B(x2;y2;z2). 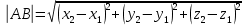 |
 Вычисление координат вектора Вычисление координат вектора 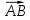 . Если А(x1;y1;z1), B(x2;y2;z2). . Если А(x1;y1;z1), B(x2;y2;z2). 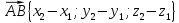 |
| Скалярное произведение векторов 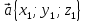 и и 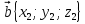 выражается формулой: выражается формулой: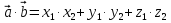 |
| Перпендикулярность векторов: 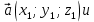 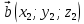 ; ;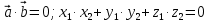 |
| Коллинеарность векторов: 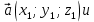 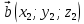 ; ; 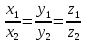 , если координаты векторов не равны нулю. , если координаты векторов не равны нулю. |
| Косинус угла между ненулевыми векторами векторов 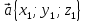 и и 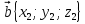 вычисляется по формуле: вычисляется по формуле: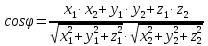 |
Задачи по теме «векторы в пространстве»
А
1.Даны координаты точек А(-3; 2; -1), В(2; -1;-3), С(1; -4; 3), Д(-1; 2; -2).
Найдите | 2АВ+3СД |
Решение:
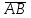 (2+3; -1-2;-3+1)=(5;-3;-2)
(2+3; -1-2;-3+1)=(5;-3;-2)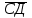 (-1-1;2+4;-2-3)=(-2;6;-5).
(-1-1;2+4;-2-3)=(-2;6;-5).2
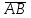 +3
+3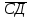 =(10+(-6);-6+18;-4-15)=(4;12;-19).
=(10+(-6);-6+18;-4-15)=(4;12;-19).
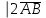 +3
+3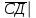 =
=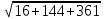 =
=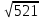
Ответ:
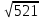
2. Даны координаты точек С(3; -2; 1), Д(-1; 2; 1), М(2; -3;3), N(-1; 1; -2). Найдите косинус угла между векторами
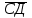 и
и 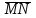 .
.Решение:
cosα=

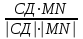
CД(-4;4;0)
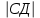 =
=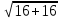 =4
=4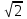
MN=(-3;4;-5)
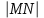 =
=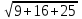 =5
=5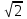
Cosα=
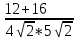 =
=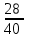 =0,7
=0,7Ответ:0,7
3. Вычислите угол между векторами
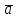 (2; -2; 0) и
(2; -2; 0) и 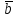 (3; 0; -3).
(3; 0; -3). Решение:
Cos
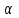 =
=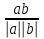
ab=2*3+(-2)*0+(-3)*0=6
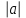 =
=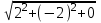 =2
=2
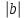 =
=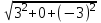 =3
=3
cos
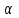 =
=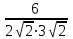 =
=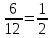
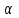 =600
=600Ответ :600
4. При каком значении n данные векторы перпендикулярны:
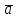 (2; -1;3) и
(2; -1;3) и 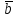 (1;3; n)?
(1;3; n)?Решение:
ab=2*1-3*(-1)+3n
3n-1=0
3n=1
n=
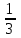
Ответ:
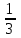
5.Вычислите координаты вектора 2
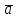 +3
+3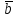 +
+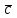 по координатам векторов:
по координатам векторов: 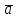 (3;1; 1),
(3;1; 1), 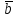 (-2;0;2)
(-2;0;2)Решение:
2
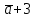
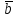 +
+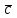 =(2*3;2*1;2*1)+(3*(-2);3*0;3*2)+(1;-1;0)=(6-6+1;2+0-1;2+6)=(1;1;8)
=(2*3;2*1;2*1)+(3*(-2);3*0;3*2)+(1;-1;0)=(6-6+1;2+0-1;2+6)=(1;1;8)Ответ:(1;1;8)
6.Вычислите значение k , при котором скалярное произведение векторов
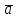 (2;k;-1) и
(2;k;-1) и 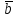 (3; -1; 2k) равно(-5)
(3; -1; 2k) равно(-5)Решение:
ab=2*3-k-2k