Файл: Методическое пособие 1011 классов с. Мичуринское удк 371. 3 Ббк 74. 262. 21 В27 Рецензентты.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 74
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 =2i+j-3k.
=2i+j-3k.Решение:
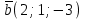
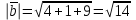
Ответ:
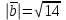
23.Найдите косинус угла между векторами
 -
-  и
и  +
+ , если
, если (1;2;1) и
(1;2;1) и (2;-1;0).
(2;-1;0).Решение:
 cos
cos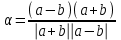
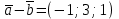
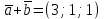
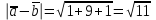
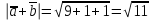
cos
 =
=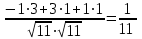
Ответ:cos

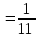
24.Найдите скалярное произведение векторов
 и
и , если |
, если | |=1, |
|=1, | |=2, |a+b|=3.
|=2, |a+b|=3.Решение:
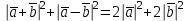
9+
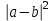 =2+8
=2+8a-2ab+b
 =10-9
=10-9-2ab+1+4=1
-2ab=-4
ab=2
Ответ:2
25.Найдите угол между векторами р=2
 +3
+3 и q=2
и q=2 -3
-3 , если
, если =i-j+2kи
=i-j+2kи  =2i+2j
=2i+2jРешение:
cos
 =
=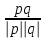 . а(1;-1;2) b(2;2;0)
. а(1;-1;2) b(2;2;0)p(2*1;2*(-1);2*2+3*2;3*2;3*0)=(8;4;4)
q(2*1;2*(-1);2*2+-3*2;3*2;3*0)=(-4;-8;4)
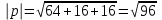
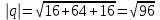
pq=-4*8-8*4+4*4=-32-32+16=-48
cos
 =
=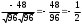
Ответ:cos
 =
=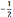
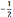
26.В параллелограмме АВСД заданы АВ(-4;-4;-2), СВ(-3;-6;1) и А(3;8;-5). Найдите сумму координат точки пересечения диагоналей.
Решение:
Пусть В( х1;у1;z1) и С(х;у;z)
х
 -3=-4 -1-х=-3
-3=-4 -1-х=-3х1=-1 х=2
у
 -8=-4 4-у=-6
-8=-4 4-у=-6у
 =4 у=10
=4 у=10z
 +5=-2 -7-z=1
+5=-2 -7-z=1z
 =-7 z=-8
=-7 z=-8B(-1;4;-7) С(2;10;-8)

О(
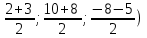 =(
=(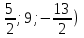
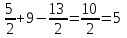
Ответ:5
27.Длина вектора
 (х;у;z) равна 5. Найдите ординату вектора
(х;у;z) равна 5. Найдите ординату вектора , если х=2, z=-
, если х=2, z=-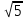
Решение:
 (2;у;-
(2;у;-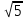 )
)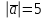
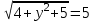
4+у
 +5=25
+5=25у
 =25-9
=25-9у
 =16
=16y =
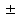 4
4Ответ:
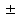 4
428.Даны три точки А(1;0;1), В(-1;1;2) и С(0;2;-1). Найдите точку Д(х;у;z), если векторы АВ и СД равны.
Решение:
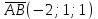
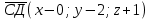
х-0=-2 у-2=1 z+1=1
х=-2, у=3, z=0
Д(-2;3;0)
Ответ:Д(-2;3;0)
В

29.При каком значении (значениях) k векторы
 (6-k;k;2) и
(6-k;k;2) и  (-3;5+5k;-9) перпендикулярны?
(-3;5+5k;-9) перпендикулярны? Решение:
 =0
=0-3(6-k)+k(5+5k)-18=0
-18+3k+5k+5k
 -18=0
-18=05k
 +8k-36=0
+8k-36=0(+)=-8
(*)=-180
k
 =
=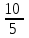 =2 k
=2 k =-
=-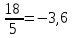
Ответ:k
 =2, k
=2, k
=
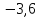
30.При каком значении а векторы АВ и СД коллинеарны, если А(-2;-1;2), В(4;-3;6),
С(-1;а-1;а), Д(-4;-1;а)?
Решение:
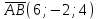
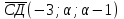
 =
= - свойство коллинеарных векторов
- свойство коллинеарных векторов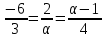
6a=-6
a=-1
Ответ:-1
31.Дано: |
 |=4, |
|=4, | |=1.
|=1.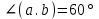 . Найдите cosa, где а – угол между векторами
. Найдите cosa, где а – угол между векторами  -
-  и
и 
Решение:
cos
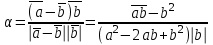
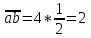
cos
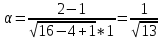
Ответ:cos
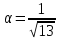
32.Найдите длину вектора a+b+c, если |a|=1 |b|=2, |c|=3,.
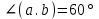 ,
,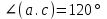 .
.Решение:
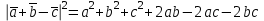
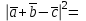 1+4+9+2(2
1+4+9+2(2
 0+3
0+3

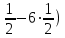
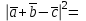 14+2
14+2
 (-
(-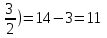
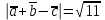
Ответ:
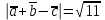
33.В параллелограмме АВСД заданы СД(-3;4;2), СИ(5;-2;4) и А(5;8;0). Найдите расстояние от точки С до начала координат.
Решение:
x
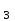 -x
-x =-3 y
=-3 y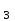 -y
-y =4 z
=4 z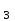 -z
-z =2
=2x
 -x
-x =5 y
=5 y -y
-y =-2 z
=-2 z -z
-z =4
=4x
 +x
+x =2+2x
=2+2x y
y +y
+y =2+2y
=2+2y z
z +z
+z =6+2z
=6+2zx
 +5=x
+5=x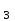 +x
+x y
y +8=y
+8=y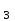 +y
+y z
z +0=z
+0=z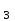 +z
+z
x
 +5=2+2x
+5=2+2x y
y +8=2+2y
+8=2+2y