Файл: Методическое пособие 1011 классов с. Мичуринское удк 371. 3 Ббк 74. 262. 21 В27 Рецензентты.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 72
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 5
5
 0=0
0=0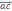
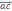 =3
=3
 8
8

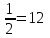
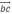
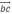 =5
=5
 8
8

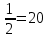
3ab+9ac-2b
 -6bc=3
-6bc=3
 0+9
0+9
 12-2
12-2
 25-6
25-6
 20
20 -
-
 +
+ =108-50-120=-62
=108-50-120=-62Ответ:-62
43.Треугольная пирамида задана координатами своих вершин А(3;0;1), В(-1;4;1), С(5;2;3) и Д(0;-5;4). Вычислите длину вектора
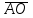 , если О – точка пересечения медиан треугольника ВСД.
, если О – точка пересечения медиан треугольника ВСД.Решение:
О – центр тяжести (
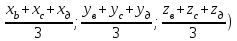
О(
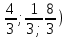
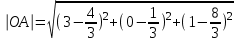 =
=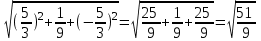
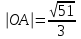
Ответ:
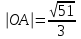
44.
 =2,
=2,  =3,
=3, 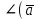 ,
, )=120. Найдите cos
)=120. Найдите cos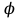 , где
, где 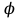 - угол между векторами
- угол между векторами  и
и +
+ .
.Решение:
cos
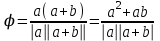
ab=2

 3
3
 (-
(-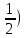 =-3
=-3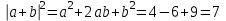
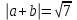
cos
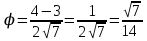
Ответ:cos
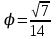
45. Треугольник задан координатами своих вершин А(1;1;2), В(3;4;2) и С(5;6;4). Найдите величину внешнего угла треугольника при вершине В.
Решение:
сos
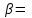
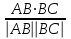
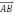
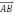 (2;0;3)
(2;0;3) 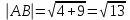

 (2;2;2)
(2;2;2) 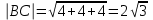
cos
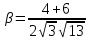 =
=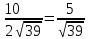
Ответ:
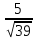
46.В треугольнике АВС точки M и N – середины сторон АВ и ВС соответственно. Известно, что
 (3;-5;6),
(3;-5;6),  (-2;1;7). Найдите сумму координат вектора
(-2;1;7). Найдите сумму координат вектора 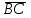 .
.Решение:
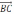
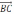 (х
(х -х
-х ; у
; у -у
-у ; у
; у -у
-у )
)М(
 )
)N(
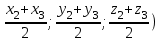

 (х
(х -х
-х ;у
;у -у
-у ;z
;z -z
-z )
)
 (х2-х1;у2-у1;z
(х2-х1;у2-у1;z -z
-z )⇒ х
)⇒ х -х
-х =3 у
=3 у -у
-у =-5 z
=-5 z -z
-z =6
=6

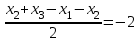
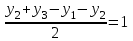
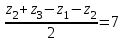
х
 -х
-х =3 у
=3 у -у
-у =-5 z
=-5 z -z
-z =6
=6x
 -x
-x =-4 y
=-4 y -y
-y =2 z
=2 z -z
-z =14
=14х
 -х
-х =-7 у
=-7 у -у
-у =7 z
=7 z -z
-z =8
=8
 (-7;7;8)
(-7;7;8)
 ⇒
⇒  -7+7+8=8
-7+7+8=8Ответ:8
47. Найдите сумму целых значений параметра b, при которых векторы
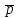 (х
(х ;х; 16) и
;х; 16) и 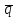 (1;b;-
(1;b;-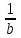 )
) при всех значениях х образуют острый угол.
при всех значениях х образуют острый угол.Решение:
p

 q>0
q>0x
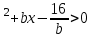
b
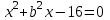
D=b
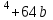
b
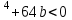
b

0
 (b
(b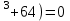 + - - +
+ - - +b=0 иb
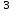 =-64 -4 0
=-64 -4 0b=-4
(-4;0)
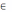
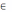 -3;-2;-1
-3;-2;-1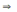
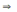 -3-2-1=-6
-3-2-1=-6Ответ :-6
48.В пространстве расположены три точки, заданные своими координатами: A(1; 6; 3), B (3; − 1; 7) и C(− 4; 3; − 2). Найти координаты векторов
 ,
, 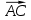 и
и 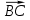 .
.Решение:
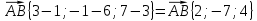
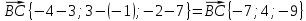
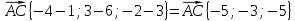
Ответ:
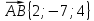 ;
; 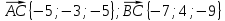
49.Вычислить скалярное произведение векторов
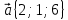 и
и 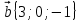
Решение:
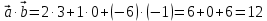
Ответ:12
50. Коллинеарны ли векторы:
a)
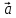 {-5;3;-1} и
{-5;3;-1} и 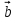 {-10; 6;-2};
{-10; 6;-2}; b)
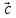 {-6;3;-1} и
{-6;3;-1} и 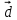 {2; -9;3};
{2; -9;3}; Решение:
a)
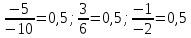
Да, векторы коллинеарны
b)
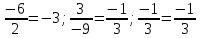
Нет, векторы не коллинеарны
Ответ: a) да b) нет
51. Найти косинус угла между векторами