Файл: Методическое пособие 1011 классов с. Мичуринское удк 371. 3 Ббк 74. 262. 21 В27 Рецензентты.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 75
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
z +0=6+2z
+0=6+2z
x =3 y
=3 y =6 z
=6 z =-6
=-6
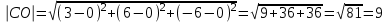
Ответ: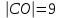
34.Точки А(14;-8;-1), В(7;3;-1), С(-6;4;-1), Д(1;-7;-1) являются вершинами ромба АВСД. Найдите острый угол ромба
Решение:
cos =
=
AB(7;11;0) ВС(-13;1;0)
АВ*ВС=91+11=102
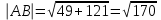
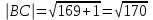

cos =
=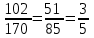
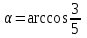
Ответ: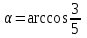
35. Дан треугольник с вершинами в точках А(3;-2;1), В(3;0;2), С(1;2;5). Найдите угол, образованный медианой ВД и основанием АС.
Решение:
точка Д середина отрезка АС АС (
АС ( )
)
Д(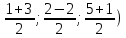 =(2;0;3)
=(2;0;3)
cos =
=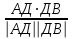
АД(-1;2;2) ВД(-1;0;1)
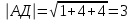
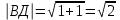
cos =
=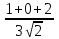 =
=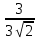 =
=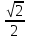


Ответ:
36.В правильном тетраэдре ДАВС с ребром а точка О – центр треугольника АВС. Найдите |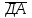 +
+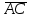 -
-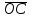 |.
|.
Решение:
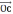
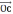 = -
= -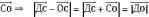
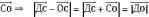
ОВ=R=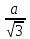
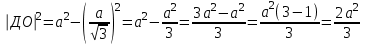
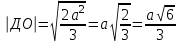
Ответ: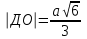
37.Даны три точки: А(1;0;10, В(-1;1;2), С(0;2;-1). Найдите на оси Оz такую точку Д(0;0;с), чтобы векторы
 и
и  были перпендикулярны.
были перпендикулярны.
Решение:
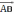
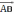
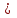
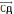
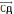 векторы перпендикулярны тогда их скалярное произведение равно нулю.
векторы перпендикулярны тогда их скалярное произведение равно нулю.
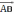
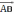 (-2;1;1)
(-2;1;1) 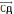
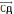 (0;-2;с+1)
(0;-2;с+1)
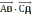
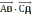 =0-2+с+1=с-1
=0-2+с+1=с-1
с-1=0
с=1
Ответ:1
38.В тетраэдре ДАВС ДА=ДВ=ДС,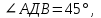
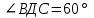 . Вычислите угол между векторами : а)
. Вычислите угол между векторами : а) 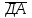 и
и 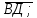
б)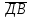 и
и 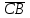 .
.
Решение:
Треугольник СДВ равнобедренный, значит углы при основании равны.
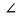 Д=
Д=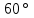

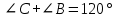
Угол между векторами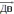
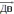 и
и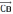
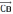 равен
равен 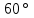
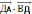
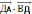 =
=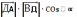
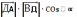 ⇒ cos
⇒ cos =
=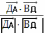
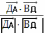
cos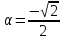
 ⇒
⇒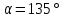
Ответ:600 ; 1350
39. При каком значении а три точки А(2;а; 3), В(3;1;6), С(4;3;9) лежат на одной прямой?
Решение:
А В С
Векторы
 и
и 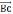
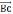 коллинеарные
коллинеарные 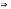
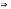



 (1;1-а;3)
(1;1-а;3) 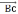
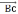 (1;2;3)
(1;2;3)
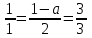
1-а=2
-а=1
а=-1
Ответ:-1
40.Найдите длину интервала значений параметра а, при которых р(-1;2х;х ) и q(5;а;а) при любом х образуют тупой угол.
) и q(5;а;а) при любом х образуют тупой угол.
Решение:
pq<0
-5+2xa+x a<0
a<0
x a+2xa-5<0
a+2xa-5<0
D=4а+20а<0
4

 a(a+5)=0+ - - +
a(a+5)=0+ - - +
a=0 a=-5 -5 0
0-(-5)=5
Ответ:5
41. Найдите длину вектора -
- -
- ,если |
,если | |=2, |
|=2, | |=3 ,|
|=3 ,| |=4, угол между
|=4, угол между  и
и  равен
равен  , между
, между  и
и 
равен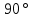 и между
и между  и
и  равен
равен 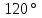 .
.
Решение:
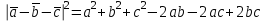 =а
=а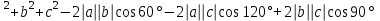
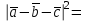 4+9+16-2
4+9+16-2
 6
6

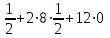
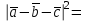 29-6+8=31
29-6+8=31
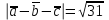
Ответ: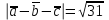
42.Векторы и
и взаимно перпендикулярны, вектор
взаимно перпендикулярны, вектор  образует с ними угол
образует с ними угол 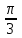 . Зная, что
. Зная, что 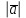 =3,
=3, 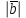 =5,
=5, 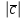 =8, вычислите скалярное произведение
=8, вычислите скалярное произведение 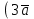 -
-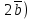
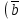 +
+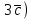 .
.
Решение:
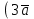 -
-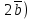
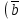 +
+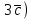 =3ab+9ac-2b
=3ab+9ac-2b -6bc
-6bc
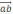
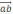 =3
=3
 +0=6+2z
+0=6+2z
x
 =3 y
=3 y =6 z
=6 z =-6
=-6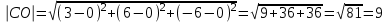
Ответ:
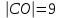
34.Точки А(14;-8;-1), В(7;3;-1), С(-6;4;-1), Д(1;-7;-1) являются вершинами ромба АВСД. Найдите острый угол ромба

Решение:
cos
 =
=
AB(7;11;0) ВС(-13;1;0)
АВ*ВС=91+11=102
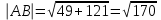
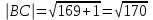

cos
 =
=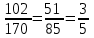
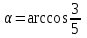
Ответ:
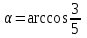
35. Дан треугольник с вершинами в точках А(3;-2;1), В(3;0;2), С(1;2;5). Найдите угол, образованный медианой ВД и основанием АС.
Решение:
точка Д середина отрезка АС
 АС (
АС ( )
)Д(
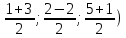 =(2;0;3)
=(2;0;3)cos
 =
=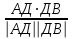
АД(-1;2;2) ВД(-1;0;1)
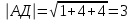
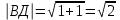
cos
 =
=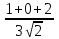 =
=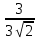 =
=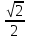


Ответ:

36.В правильном тетраэдре ДАВС с ребром а точка О – центр треугольника АВС. Найдите |
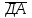 +
+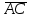 -
-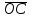 |.
|.Решение:
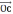
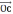 = -
= -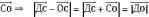
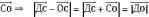
ОВ=R=
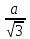
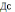
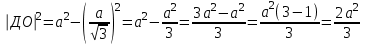
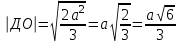
Ответ:
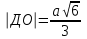
37.Даны три точки: А(1;0;10, В(-1;1;2), С(0;2;-1). Найдите на оси Оz такую точку Д(0;0;с), чтобы векторы

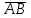 и
и  были перпендикулярны.
были перпендикулярны. Решение:
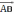
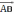
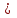
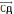
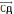 векторы перпендикулярны тогда их скалярное произведение равно нулю.
векторы перпендикулярны тогда их скалярное произведение равно нулю.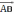
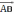 (-2;1;1)
(-2;1;1) 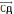
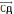 (0;-2;с+1)
(0;-2;с+1)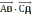
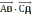 =0-2+с+1=с-1
=0-2+с+1=с-1с-1=0
с=1
Ответ:1
38.В тетраэдре ДАВС ДА=ДВ=ДС,
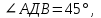
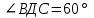 . Вычислите угол между векторами : а)
. Вычислите угол между векторами : а) 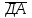 и
и 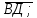
б)
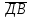 и
и 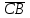 .
.Решение:
Треугольник СДВ равнобедренный, значит углы при основании равны.
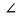 Д=
Д=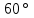

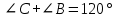
Угол между векторами
 и
и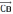
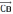 равен
равен 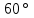
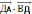
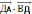 =
=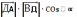
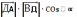 ⇒ cos
⇒ cos =
=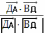
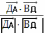
cos
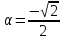
 ⇒
⇒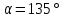
Ответ:600 ; 1350
39. При каком значении а три точки А(2;а; 3), В(3;1;6), С(4;3;9) лежат на одной прямой?
Решение:
А В С
Векторы

 и
и 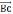
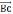 коллинеарные
коллинеарные 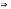
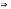



 (1;1-а;3)
(1;1-а;3) 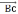
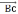 (1;2;3)
(1;2;3)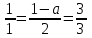
1-а=2
-а=1
а=-1
Ответ:-1
40.Найдите длину интервала значений параметра а, при которых р(-1;2х;х
 ) и q(5;а;а) при любом х образуют тупой угол.
) и q(5;а;а) при любом х образуют тупой угол. Решение:
pq<0
-5+2xa+x
 a<0
a<0x
 a+2xa-5<0
a+2xa-5<0D=4а+20а<0
4


 a(a+5)=0+ - - +
a(a+5)=0+ - - +a=0 a=-5 -5 0
0-(-5)=5
Ответ:5
41. Найдите длину вектора
 -
- -
- ,если |
,если | |=2, |
|=2, | |=3 ,|
|=3 ,| |=4, угол между
|=4, угол между  и
и  равен
равен  , между
, между  и
и 
равен
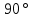 и между
и между  и
и  равен
равен 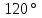 .
.Решение:
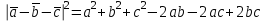 =а
=а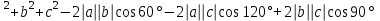
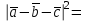 4+9+16-2
4+9+16-2
 6
6

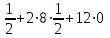
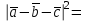 29-6+8=31
29-6+8=31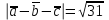
Ответ:
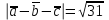
42.Векторы
 и
и взаимно перпендикулярны, вектор
взаимно перпендикулярны, вектор  образует с ними угол
образует с ними угол 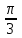 . Зная, что
. Зная, что 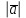 =3,
=3, 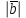 =5,
=5, 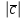 =8, вычислите скалярное произведение
=8, вычислите скалярное произведение 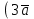 -
-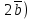
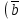 +
+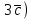 .
.Решение:
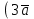 -
-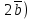
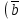 +
+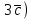 =3ab+9ac-2b
=3ab+9ac-2b -6bc
-6bc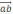
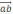 =3
=3